輪轂電機電動汽車半主動懸架模型預測控制

江 洪，陳 勃，吳楚騏

(江蘇大學 機械工程學院，江蘇 鎮江 212013)

0 引言

目前，電動汽車因具有能源利用率高、污染少等優點得到快速發展。隨著汽車保有量的迅速增加、環境污染以及能源短缺等問題日益嚴重，發展電動汽車已成為實現節能減排、減少環境污染的有效途徑，近年來輪轂電機電動汽車的使用率不斷提高[1]。

懸架系統關系到車輛的乘坐舒適性和行駛安全性，選擇合理的控制策略，以及使用有效的控制算法對提升半主動懸架系統的減振性能具有關鍵作用[2]。空氣懸架屬于半主動懸架，具有壽命長、內摩擦小、質量輕等優點，可有效改善車輛行駛平順性，對高頻振動具有很好的消聲隔振能力[3]。阻尼可調空氣懸架由于其彈簧剛度和減振器阻尼均可調、能吸收高頻振動、隔振性能好等優勢在汽車行業得到快速發展[4]。

輪轂電機電動汽車取消了離合器、變速器、傳動軸、差速器等部件，使底盤結構得到進一步簡化，可以實現四輪獨立驅動，使控制更加精確，有效提高了車輛行駛的穩定性[5]。面對輪轂電機驅動汽車非簧載質量增加和輪轂電機不平衡電磁力帶來的振動負效應問題，李仲興等[6]提出了一種自適應線性二次型調節器半主動懸架控制策略，有效提高了車輛的行駛平順性和操縱穩定性。陳龍等[7]為提高車輛行駛平順性，提出了一種基于阻尼多模式切換減振器的車輛半主動懸架及其控制方法。

董炳辰等[8]為了提高車輛行駛平順性和操作穩定性，以工程車輛半主動懸架為研究對象，基于比例積分微分和增量式算法原理，提出了一種用于工程車輛半主動懸架的增量式PID控制方法。馬英照等[9]開發了新型空氣懸架系統集成控制系統，有效改善了車輛的穩定性。李哲等[10]為控制車輛垂向振動，對控制器參數進行了多目標優化。武柏安等[11]提出了一種基于遺傳算法的半主動懸架最優控制方法，應用遺傳算法來確定最優控制器的加權系數，提高了車輛的平順性。趙亮亮等[12]為抑制路面不平引起的車身振動響應問題，搭建了半車半主動懸架仿真模型，設計了半主動懸架控制器，有效提高了車輛行駛的舒適性。

以上學者為抑制輪轂電機振動和提升懸架性能，對車輛懸架和輪轂電機控制系統進行了研究和改進，大多數學者考慮使用四分之一車輛模型或半車車輛模型對懸架系統進行控制研究，本文通過建立整車九自由度懸架系統模型，提出一種在處理多輸入多輸出控制系統中具有突出優勢的半主動懸架模型預測控制方法，有效地改善了輪轂電機電動汽車的垂向性能。

1 HM-EV系統建模

輪轂電機電動汽車懸架系統是復雜的機電耦合系統，包括輪轂電機、懸架和車輪。整車9自由度HM-EV模型包括3部分：無刷直流電機(brushless direct current motor，BLDC)模型，該部分的模型可為車輪和懸架提供不平衡電磁力；路面隨機激勵模型，為系統提供外部激勵；整車動力學模型，強調車輛的動態響應。

1.1 不平衡電磁力模型

BLDC電機具有傳動效率高、結構緊湊等優點。本文采用外轉子BLDC電機作為輪轂驅動電機。

外轉子BLDC的電流方程如下：

(1)

式中：ua、ub和uc分別為電機三相電壓，V；R表示定子繞組的等效電阻，Ω；L表示輪轂電 機定子繞組自感，H；M表示繞組互感，H；ia、ib和ic分別為輪轂電機三相電流，A；ea、eb和ec分別為輪轂電機三相繞組反電動勢，V。

在不考慮各種損耗的情況下，認為電機的輸入功率全部轉換為電磁功率，因此電機的電磁轉矩方程可表示為：

(2)

式中：Te為電機電磁轉矩，N·m；ωm為轉子角速度，rad/s。

輪轂電機電動汽車在路面激勵和簧載質量的耦合作用下，定轉子間會發生相對位移，輪轂電機產生偏心現象，電機氣隙分布不均，氣隙磁場會產生畸變，從而誘發不平衡電磁力，導致電機不良振動。為分析偏心狀態下的輪轂電機氣隙磁場，采用磁導修正系數的方法[13-14]，對無偏心狀態下的輪轂電機的氣隙磁場進行修正，以獲得偏心狀態下的氣隙磁場。BLDC輪轂電機偏心示意圖如圖1所示。

圖1 輪轂電機定轉子偏心示意圖

圖1中，O為輪轂電機外轉子的幾何中心，O′為輪轂電機內定子的幾何中心，e為電機偏心距，即電機定子中心O′與轉子中心O的距離。則有效氣隙長度δ計算滿足：

(3)

式中：δ0為電機實際氣隙長度，m；hm為永磁體厚度，m；μr為相對回復磁導率。有效偏心率ε滿足：

(4)

則偏心時的磁導修正系數為：

(5)

則輪轂電機偏心狀態下氣隙徑向磁場Ber和氣隙切向磁場Bet計算式為：

Ber(r,α,t)=[Bmr(r,α,t)+Bαr(r,α,t)]εδ

(6)

Bet(r,α,t)=[Bmt(r,α,t)+Bαt(r,α,t)]εδ

(7)

式中：r為極坐標系極徑，m；α為極坐標系空間角度，rad；t為時間，s；Ber為偏心狀態下的徑向氣隙磁場；Bmr為永磁體的徑向磁場；Bαr為電樞反應的徑向磁場；Bet為偏心狀態下的切向氣隙磁場；Bmt為永磁體的切向磁場；Bαt為電樞反應的切向磁場。

根據文獻[15]提出的氣隙磁密公式，輪轂電機垂向不平衡電磁力Fez和縱向不平衡電磁力Fex可表示為：

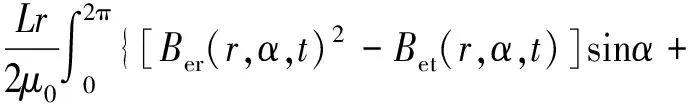
2[Ber(r,α,t)2·Bet(r,α,t)]cosα}dα

(8)

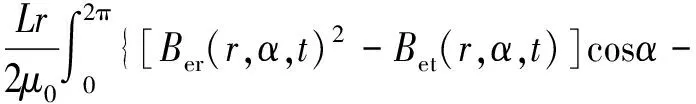
2[Ber(r,α,t)2·Bet(r,α,t)]sinα}dα

(9)

式中L為電機軸向長度，m。

1.2 路面隨機激勵模型

路面是懸架系統的主要激勵，在實際道路上行駛時，由于左右兩側路面具有相干性，前后輪具有滯后性，需要建立整車四輪隨機路面激勵的時域模型，因此建立考慮前左輪路面激勵、前右輪路面激勵和后軸路面激勵的四輪車輪隨機路面激勵模型。

1.2.1前左輪路面激勵

路面激勵服從均值為零的正態分布，并以功率譜來描述其統計特性。根據國標GB/T 7031—2005，可用下式表示路面不平度的頻率譜密度：

(10)

式中：n為空間頻率，m-1；n0為參考空間頻率，取值0.1 m-1；Gq(n0)為參考空間頻率下的功率譜密度，m3；W為頻率指數，W=2，其值決定了路面功率譜的頻率結構。

根據GB/T 7031—2005標準規定，路面空間頻域速度功率譜密度為：

(11)

道路速度信號是具有有限帶寬的白噪聲，因此白噪聲可以通過濾波生成道路高程的時域信號。過濾器為

(12)

式中：f0為截止頻率，f0=0.01 Hz。則路面時域信號為：

(13)

式中，ω(t)為白噪聲。

1.2.2前右輪路面激勵

車輛在行駛過程中，考慮到路面不平，因此左右兩側車輪受到的路面激勵也有差異，為了描述左右兩側車輪受到的路面激勵，可用相干度函數γ來表示：

(14)

式中：Tw為輪距，m；p為參考因子；α為輪距Tw的常數指數，對于各向同性過程，α=1。

對于給定的左右路面激勵q1(t)和q2(t)，則q1(t)對q2(t)的傳遞函數G(s)可寫作：

(15)

式中，Q1(s)和Q2(s)分別為q2(t)和q1(t)的拉普拉斯變換。結合(14)和(15)兩式，則

|G(s)|=|γ(n,Tw)|

(16)

則車輛前軸左右兩側路面激勵：

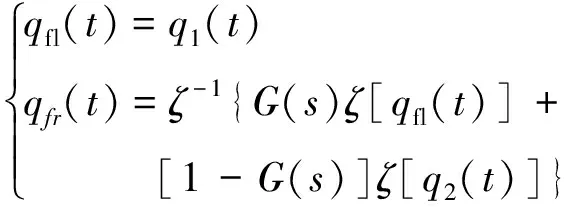
(17)

1.2.3后軸左右路面激勵

假設車輛直線行駛，此時車輛前后兩輪行駛過的路面大致相同，但后輪路面激勵相較于前輪路面激勵存在一定的滯后。后輪左右路面激勵為：

(18)

式中，t≥τ，τ為滯后時間，為車輛軸距與車速的商。

為解決滯后難以線性化的問題，可通過復數域利用傳遞函數來描述：

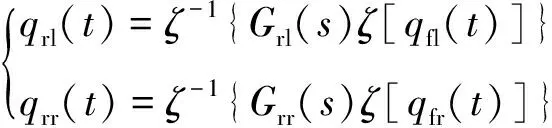
(19)

式中，Grl(s)和Grr(s)分別為qrl(t)對qrr(t)的傳遞函數和qrr(t)對qrr(t)的傳遞函數。

根據以上四輪路面激勵模型，在C級路面，車速為20 m/s的行駛工況下，各輪對應的路面激勵幅值如圖2所示。

圖2 C級路面四輪激勵幅值

1.3 輪轂電機電動汽車半主動懸架整車動力學模型

車輛動力學模型作為半主動懸架控制的基礎，其精度對懸架控制精度具有重要作用，同時也會影響控制器的計算能力，因此，設計合適的車輛動力學模型以及使用匹配的控制器直接影響半主動懸架系統的控制效果。

本文采用一體式輪轂電機與空氣懸架系統，結構如圖3所示，包括輪胎、輪轂電機、電控裝置、制動器、輪轂以及空氣懸架系統。輪轂電機為外轉子內定子結構，輪轂軸承作為運動連接件和載荷支撐件，在垂向等效為高剛度彈簧，空氣懸架系統包括空氣彈簧和減振器，電機轉子固定在輪轂上。在對懸架的控制理論和概念進行研究時，整車模型可完整的體現車輛的垂直跳動、側傾變化以及俯仰的問題。

圖3 輪轂電機與空氣懸架結構示意圖

根據后續研究需要，建立以試驗樣車實際結構為依據的九自由度整車動力學模型，該車型采用的是后輪輪轂電機驅動方式，假設車身為剛體，只考慮系統的垂向振動，并對其進行適當簡化。前輪位置考慮2個簧下質量的垂向振動、后輪以輪轂電機氣隙為分界面，將輪轂電機外轉子和內定子拆分，將電機軸承等效為高剛度彈簧，從而簧下質量分為2個部分：一部分是由定子質量塊和部分非簧載質量塊組成的振動系統，另一部分是由轉子質量塊和輪胎組成的振動系統、以及簧上質量的側傾、俯仰和垂向振動，共9個自由度。簡化后的半主動空氣懸架九自由度整車模型如圖4所示。

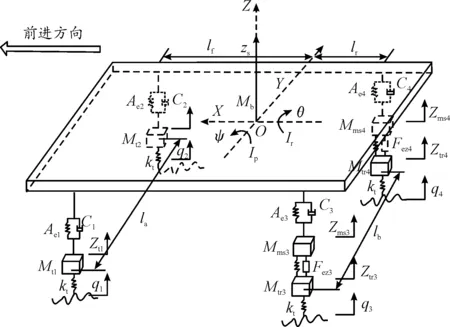
圖4 整車空氣懸架動力學模型示意圖

根據車輛動力學，該后輪輪轂電機驅動電動汽車空氣懸架系統動力學方程可表示為：

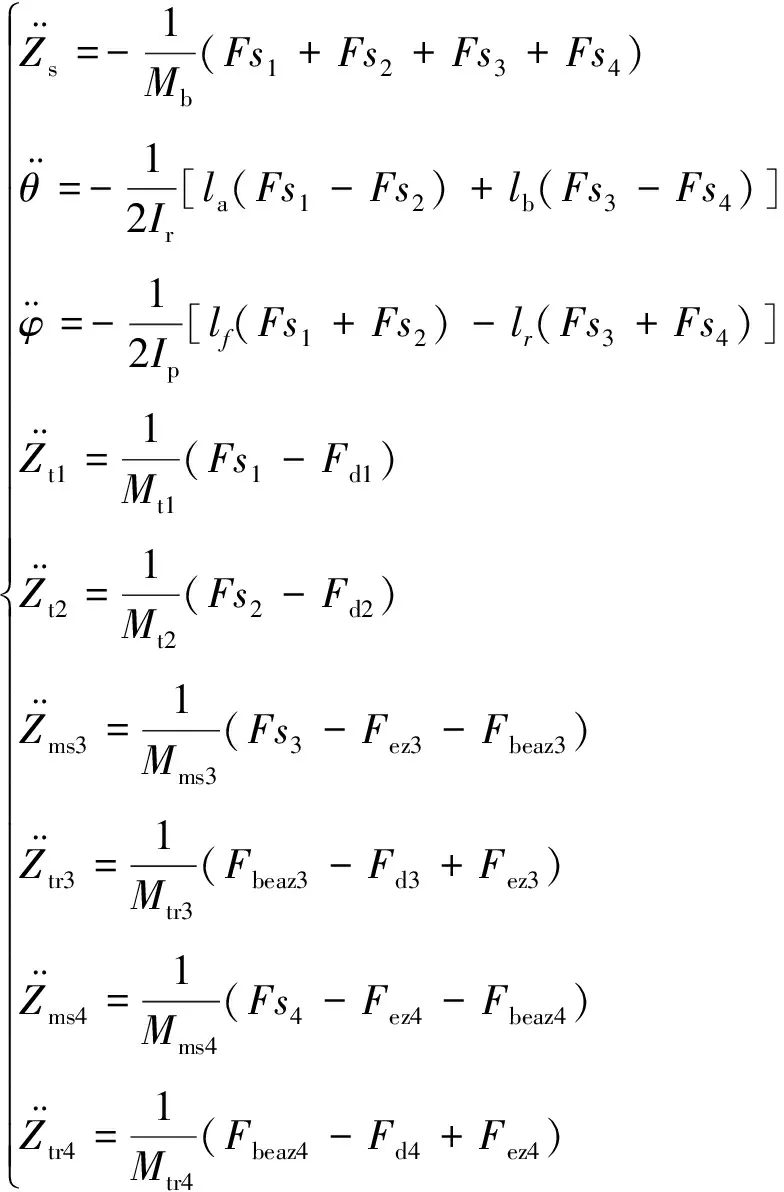
(20)

式中，

其中：Mb表示簧載質量，kg；Ir和θ分別為簧上質量繞x軸的側傾轉動慣量，kg·m2和簧上質量側傾角，rad；Ip和φ分別為簧上質量繞y軸的俯仰轉動慣量，kg·m2和簧上質量俯仰角，rad；lf和lr分別為前、后軸到質心的距離，m；la和lb分別為前、后軸車輪左右輪距，m；Mt1和Mt2分別為車輛左前輪、右前輪位置處的簧下質量，kg；Mms3和Mms4分別為車輛左后輪、右后輪輪轂電機定子鐵芯質量塊和部分非簧載質量塊質量，kg；Mtr3和Mtr4分別為車輛左后輪、右后輪輪胎和轉子鐵芯質量塊質量，kg；Zs為簧載質量垂向位移，m；Zt1和Zt2分別為左前輪、右前輪簧下質量的垂向位移，m；Zms3和Zms4分別為車輛左后輪、右后輪定子鐵芯質量塊和部分非簧載質量塊垂向位移，m；Ztr3和Ztr4分別為車輛左后輪、右后輪輪胎和轉子鐵芯質量塊垂向位移，m；q1、q2、q3、q4分別為車輛左前輪、右前輪、左后輪和右后輪位置處的路面垂向激勵，m；kt為輪胎的垂向剛度，N/m；kbe為輪轂電機軸承垂向剛度，N/m；Fez3和Fez4分別為車輛左后輪、右后輪輪轂電機垂向不平衡電磁力，N；Ae1、Ae2、Ae3和Ae4分別為車輛左前輪、右前輪、左后輪和右后輪位置處空氣彈簧初始有效面積，m2；κ為多變系數；P0為空氣彈簧初始氣壓，Pa；Pa為標準大氣壓強，Pa；C1、C2、C3和C4分別為車輛左前輪、右前輪、左后輪和右后輪位置處減振器阻尼系數，N·s/m；Fspr為空氣懸架的空氣彈簧力，N；Fdam為減振器阻尼力，N；Fd為輪胎動載荷，N；Fbeaz為輪轂電機垂向軸承力，N；Fez為輪轂電機垂向不平衡電磁力，N；fd為懸架動行程，m；Fu為懸架阻尼控制力，N。

2 輪轂電機與空氣懸架系統模型預測控制

2.1 MPC控制器設計

模型預測控制通過動態模型來預測被控對象的未來行為，通過預測模型、滾動優化以及反饋校正3個步驟完成控制過程，對處理多輸入多輸系統具有顯著優勢，在控制過程中，可增加多種模式的約束，以滿足車輛動力學的要求。在每個采樣時間內，MPC根據系統的狀態，將控制問題轉化為N步有限時域開環最優控制問題。MPC得到最優控制變量{u(k),u(k+1),…,u(k+N-1)}，通過在線計算方法將第一個控制變量u(k) 施加給系統，下一時刻根據系統輸出與預測輸出之間的誤差對未來輸出進行修正。一些研究已經將MPC控制方法應用于半主動懸架系統，然而，大多數研究只考慮了四分之一車輛模型，本文提出考慮整車模型的模型預測控制方法。根據式(20)中的動力學方程，系統的狀態空間可以表示為：

(21)

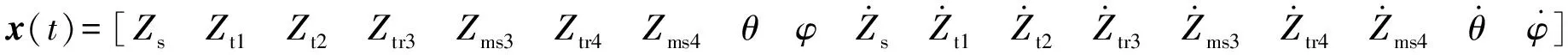
系統輸出定義為車輛簧載質量垂向振動加速度；左后輪、右后輪輪轂電機偏心距；四輪輪胎動載荷；車輛側傾角速度以及俯仰角速度。

(22)

MPC是在離散時間域求解最優問題，因此需要通過采樣時間Ts和零階保持器將已有的連續時間狀態方程進行離散化處理，離散化后的狀態方程可以表示為：

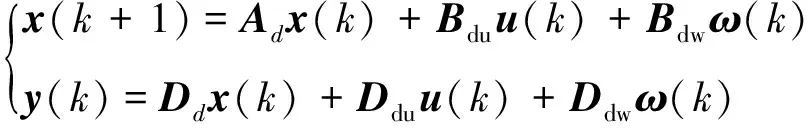
(23)

式中，

Ad=eATs=L-1{(sI-A)-1}t=Ts

Cd=C

Dd=D

其中：Ts為采樣時間；τ為積分時間常數。

2.2 約束與目標函數

考慮到懸架動行程受懸架結構約束，則對輪胎動載荷施加約束|Fdi|≤3 000 N，同時考慮控制力|Fu|≤5 000 N。

MPC控制器的目標是找到最優控制率u(k)，在約束條件下優化車輛的行駛平順性和操縱穩定性，通過求解目標函數最小值，找到當前時刻目標函數最小值的控制向量u(k)，此時u(k)中的元素即為所求控制力Fu。優化的目的是使目標函數最小，其表達式為：

(24)

式中：

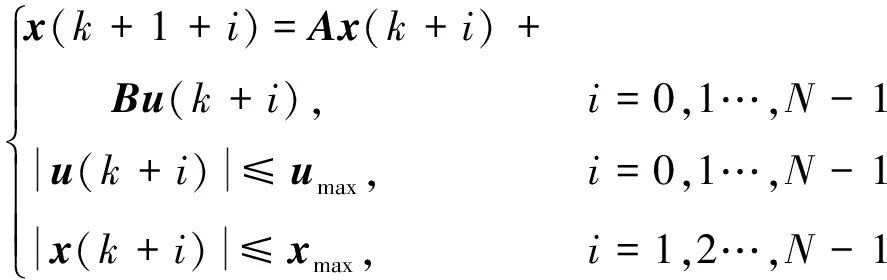
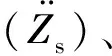
3 仿真結果

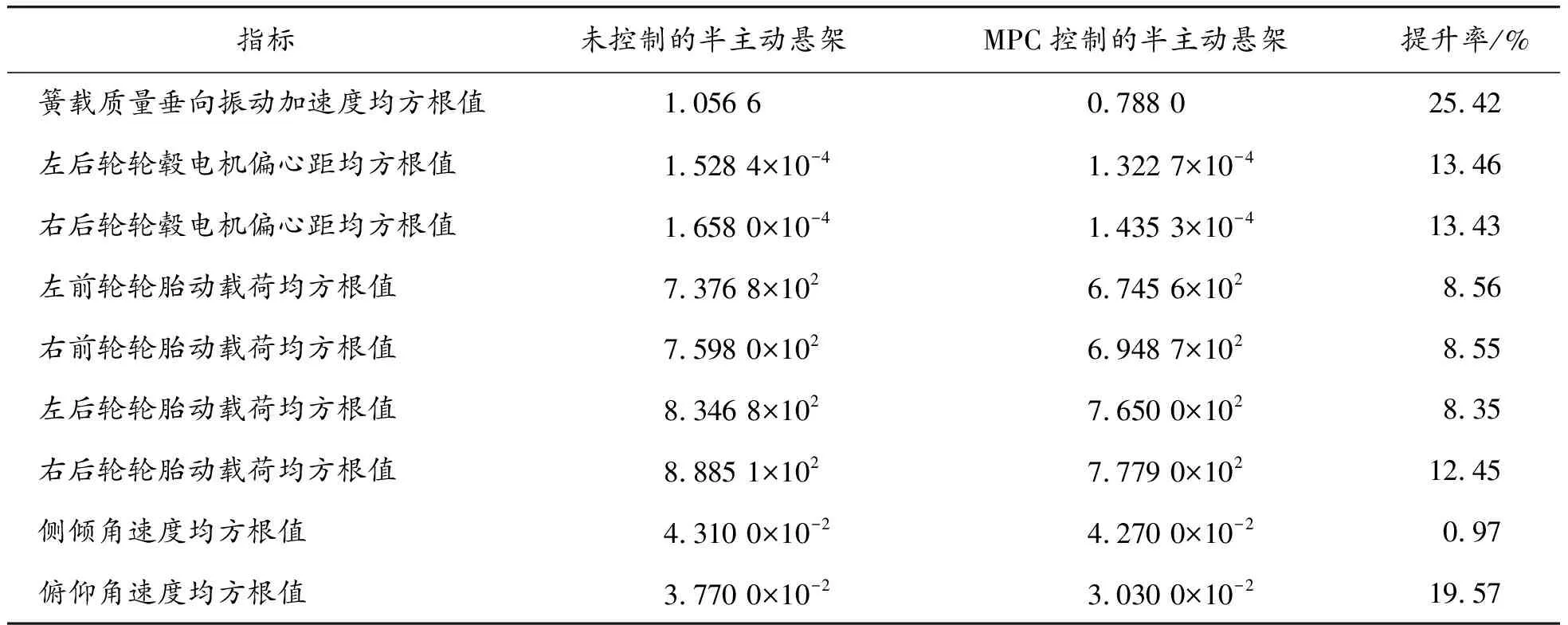
仿真模型在車速為20 m/s的C級別路面激勵輸入下穩定運行5 s。模型的相關參數如表1所示。為了體現MPC控制策略對懸架系統行駛平順性的改善效果，引入未控制的半主動懸架進行比較，仿真分析系統評價指標的時域對比效果和頻域對比效果[16]。結果如圖5、圖6和表2所示。

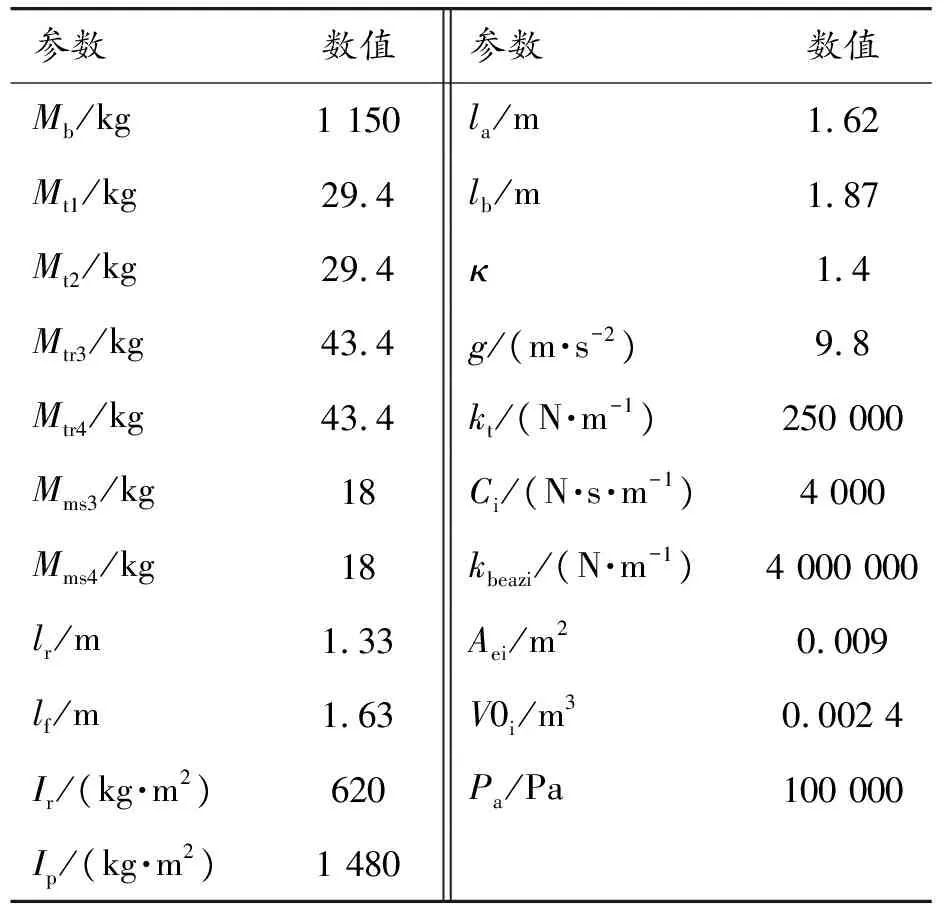
表1 模型參數

圖5 輪轂電機電動汽車系統垂向性能控制對比

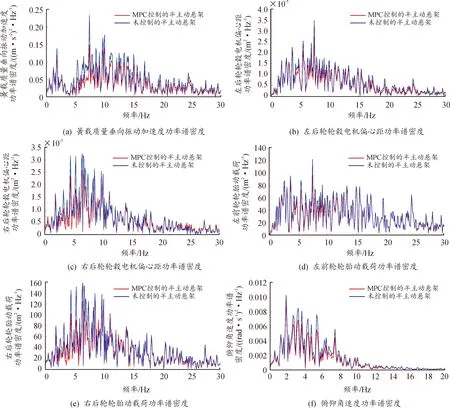
圖6 MPC控制效果功率譜密度

指標未控制的半主動懸架MPC控制的半主動懸架提升率/%簧載質量垂向振動加速度均方根值1.056 60.788 025.42左后輪輪轂電機偏心距均方根值1.528 4×10-41.322 7×10-413.46右后輪輪轂電機偏心距均方根值1.658 0×10-41.435 3×10-413.43左前輪輪胎動載荷均方根值7.376 8×1026.745 6×1028.56右前輪輪胎動載荷均方根值7.598 0×1026.948 7×1028.55左后輪輪胎動載荷均方根值8.346 8×1027.650 0×1028.35右后輪輪胎動載荷均方根值8.885 1×1027.779 0×10212.45側傾角速度均方根值4.310 0×10-24.270 0×10-20.97俯仰角速度均方根值3.770 0×10-23.030 0×10-219.57

由圖5的時域對比圖和表2可知，所設計的MPC控制器能夠有效提高系統的垂向性能。相比未控制的半主動懸架，使用MPC控制器后，車輛的簧載質量垂向振動加速度均方根值、左后輪輪轂電機偏心距均方根值、右后輪輪轂電機偏心距均方根值、左前輪輪胎動載荷均方根值、右前輪輪胎動載荷均方根值、左后輪輪胎動載荷均方根值、右后輪輪胎動載荷均方根值、側傾角速度、俯仰角速度分別提升了25.42%、13.46%、13.43%、8.56%、8.55%、8.35%、12.45%、0.97%與19.57%。

如圖6所示，將MPC控制的半主動懸架的簧載質量垂向振動加速度、輪轂電機偏心距、輪胎動載荷和俯仰角速度功率譜密度與未控制的半主動懸架進行對比。圖6(a)中，MPC控制的簧載質量垂向振動加速度在整個頻域范圍內降低幅度較大，表明MPC控制的半主動懸架可有效抑制路面激勵以及輪轂電機因偏心產生的不良振動對簧載質量振動的影響；圖6(b)和6(c)中，輪轂電機偏心距在控制后的功率譜密度在中低頻區域內降低幅度較大，高頻區域變化幅度小，從總體上看，輪轂電機偏心距降低較大，表明MPC控制器可有效降低輪轂電機偏心距；圖6(d)和6(e)中，MPC控制的輪胎動載荷功率譜密度在中低頻區域內降低較明顯，高頻區域下降趨勢小，表明MPC控制的半主動懸架可有效降低來自路面激勵和輪轂電機不平衡電磁力對輪胎動載荷的影響；圖6(f)中，MPC控制的俯仰角速度功率譜密度在中低頻區域內下降幅度大，高頻區域變化小，但保持著下降趨勢，表明MPC控制的半主動懸架可有效降低俯仰角速度。

從圖5和圖6可知，所設計的MPC控制器能有效改善懸架性能，提高輪轂電機電動汽車系統的乘坐舒適性和行駛平順性。

4 結論

本文分析了空氣懸架、輪轂電機和車輪之間的作用機理，建立了9自由度整車HM-AS系統模型。以改善簧載質量垂向振動加速度、輪轂電機偏心距、輪胎動載荷、側傾角速度和俯仰角速度為目標，提出一種基于動態模型來對系統未來行為進行預測的模型預測控制策略，使用多項評價指標全面的評價懸架性能。通過仿真的時域圖和頻域圖對比分析可知，所提出的模型預測控制方法有效地減小了簧載質量垂向振動加速度、輪轂電機偏心距、輪胎動載荷、側傾角速度和俯仰角速度，充分提高了車輛的行駛平順性和操縱穩定性，仿真分析驗證了所提MPC控制方法的有效性。