基于分類難度的過采樣度優(yōu)化方法

祝團飛，羅成，曾一夫，張維

（1.長沙學院計算機科學與工程學院，湖南 長沙 410022；2.江西工業(yè)貿易職業(yè)技術學院信息工程系，江西 南昌 330038）

不平衡數(shù)據(jù)的分類是指分類的數(shù)據(jù)中一些類（大數(shù)類）的樣本數(shù)目顯著多于另外一些類（少數(shù)類）的樣本數(shù)目，該問題廣泛地存在于現(xiàn)實世界的應用中，例如疾病診斷、軟件缺陷預測、故障偵測等。樣本數(shù)目的不平衡分布給傳統(tǒng)的分類學習算法帶來了巨大挑戰(zhàn)，主要表現(xiàn)在兩方面：分類算法通常以最小化訓練錯誤為目標，樣本數(shù)量絕對占優(yōu)的大數(shù)類會使其分類器的預測偏置［1-2］；類重疊、類內不平衡、噪聲等數(shù)據(jù)困難因子與類不平衡在學習困難度上有超疊加效應［3-4］。此兩項挑戰(zhàn)使標準的分類學習算法在少數(shù)類上的預測表現(xiàn)出低泛化性能。然而，稀有的少數(shù)類對象往往能體現(xiàn)出問題的本質，對少數(shù)類樣本錯誤地分類可能會付出相比錯誤預測大數(shù)類樣本更高的代價。例如，在疾病診斷中誤將一個健康人診斷為患某種疾病固然會給人帶來精神負擔，但將一個實際病患漏診為健康人會讓其錯過最佳的治療時機，導致災難性的后果。

過去的二十年，研究人員提出了多種類型的不平衡學習方法［5-6］。其中，人工合成少數(shù)類樣本的過采樣技術是熱門的方法之一。過采樣技術需要解決兩個基本問題：如何生成人工的少數(shù)類合成樣本，以及為每一個少數(shù)類樣本生成多少合成樣本。這兩個問題分別涉及合成樣本的生成和過采樣度的尋優(yōu)。現(xiàn)有研究中，幾乎所有的過采樣算法都側重于合成樣本的生成方法創(chuàng)新，而忽略過采樣度的尋優(yōu)策略設計。然而，過采樣度能顯著影響算法的性能，過高的過采樣度會嚴重損害大數(shù)類的分類性能，過低的過采樣度將不能有效糾正分類器偏向大數(shù)類的預測偏置。

在過采樣度尋優(yōu)策略中，一個關鍵的問題是如何解決過采樣權重分布，即在總的合成樣本一定的情況下，如何完成合成樣本在各個少數(shù)類樣本上量的分配。現(xiàn)有的方法基于樣本分布的局部特征，為少數(shù)類樣本測量若干反映學習重要性的數(shù)據(jù)因子，然后整合這些數(shù)據(jù)因子作為過采樣權重［7-11］。然而，學習的重要性依賴于具體的分類學習方法，且出于強化難于分類的樣本學習的目的，少數(shù)類樣本的過采樣度應由其本身的分類難度決定。

基于以上動機，我們提出一種依賴分類困難度的過采樣權重分配方法CD-W（Classification Difficulty-based Weighting）。通過將CD-W與目前流行的SMOTE插值生成技術相結合，得到新的過采樣算法CD-SM。CD-SM中每一個少數(shù)類樣本的過采樣權重由分類器對其預測的軟損失決定，以確保分類損失越高的少數(shù)類樣本分配到越多的合成樣本。為了評估CD-SM的有效性，我們以神經網絡為分類器，以F1、G-mean和AUC［12］為性能評價指標，在18個UCI標準數(shù)據(jù)集上進行實驗，結果表明，CD-SM是具有高度競爭力的加權過采樣算法。

1 相關工作

現(xiàn)有文獻中，只有非常少量的過采樣方法涉及估計過采樣權重的分布，我們對有限的過采樣權重估計方法進行了總結。

自2002年合成少數(shù)過采樣技術SMOTE被提出以來，學術界和工業(yè)界的研究人員設計了大量的過采樣算法去處理不平衡的分類問題［6-9，13-18］。絕大部分的算法致力于合成樣本生成方法的創(chuàng)新，而忽視過采樣度尋優(yōu)策略的設計，其中代表性的算法有SMOTE［17］、SMOM［13］、PAIO［14］和SMOR［15］。這些方法簡單地假設過采樣權重分布是一個均勻的分布，為每一個少數(shù)類樣本生成等量的合成樣本。然而，不同的少數(shù)類樣本具有不同的重要性，一些樣本可為數(shù)據(jù)的分類學習提供更多有用的信息。

Borderline-SMOTE［9］和ADASYN［7］是被最早提出加權過采樣的兩個算法，且都基于少數(shù)類樣本的k最近鄰居分布確定過采樣的權重。前者只對k最近鄰居中存在一半以上大數(shù)類樣本的少數(shù)類樣本賦權重（不包括k最近鄰居全為大數(shù)類的少數(shù)類“噪聲”樣本），后者少數(shù)類樣本的過采樣權重與其k最近鄰居中大數(shù)類樣本數(shù)目成正比。此種加權過采樣策略的動機是邊界的樣本往往具有更高的重要性，需為其分配更多的合成樣本。后續(xù)的INOS［10］和RAMOBoost［11］過采樣沿用了ADASYN的過采樣權重計算方法。然而，找到一個合適的鄰居參數(shù)k去捕捉所有的邊界樣本和充分反映學習的重要性是非常困難甚至不可行的［18］。

為避免設置參數(shù)k，MWMOTE［18］引入邊界大數(shù)類樣本和少數(shù)類樣本間的親密因子與密度因子來計算少數(shù)類樣本的過采樣度，其中親密因子衡量每一個邊界大數(shù)類樣本與其k最近的少數(shù)類樣本的鄰近程度（即距離遠近），而密度因子反映每一個邊界大數(shù)類樣本周圍分布少數(shù)類樣本的稀疏程度。一個少數(shù)類樣本的過采樣權重是累加所有邊界大數(shù)類樣本提供的親密因子與密度因子的乘積。MWMOTE分配過采樣權重的主要出發(fā)點是為越靠近大數(shù)類樣本（更高的親密因子）和位于越稀疏聚類（傾向更高的密度因子）的少數(shù)類樣本分配越高的權重。

最近，基于高斯分布的過采樣方法GDO［8］采用了與MWMOTE相似的權重計算方法，其使用密度因子和距離因子來衡量少數(shù)類樣本所具有的信息量差異。在GDO中，密度因子被定義為少數(shù)類樣本的k最近鄰居中大數(shù)類樣本的比率，距離因子衡量k最近鄰居中大數(shù)類樣本鄰居相對于少數(shù)類樣本鄰居與當前考慮的少數(shù)類樣本的平均距離比。GDO將一個少數(shù)類樣本的密度因子與距離因子之和作為此樣本的過采樣權重，其背后的動機是為遠離大數(shù)類樣本的邊界少數(shù)類樣本分配更高的權重。然而，類似于ADASYN，如果少數(shù)類樣本的k最近鄰居不存在任何的大數(shù)類樣本，GDO將為這些樣本的權重賦值為零。顯然，這可能導致大部分的過采樣權重只集中在個別的少數(shù)類樣本上。

2 基于分類難度的算法

我們提出的過采樣算法的主要思想是依據(jù)少數(shù)類的分類難度來分配少數(shù)類樣本的過采樣權重，然后與目前流行的合成樣本生成方法SMOTE相結合，得到一種基于分類難度的加權過采樣方法CD-SM。在CD-SM中，一個少數(shù)類樣本的分類難度是分類模型對其多次預測的分類損失平均。CD-SM首先將樣本的分類難度轉化為過采樣的權重分布，然后據(jù)此分布，在更難分類的少數(shù)類樣本附近插值生成更多的合成樣本，以強化這些樣本的學習。

CD-SM的算法過程如下。

輸入：原始不平衡數(shù)據(jù)集D，少數(shù)類樣本集S，分類學習算法L，估計分類難度的次數(shù)nc，生成的合成樣本總量ns；

輸出：合成的少數(shù)樣本集Syn；

步驟1：對原始不平衡數(shù)據(jù)集D的每一類，應用SMOTE方法生成相同數(shù)量的合成樣本，以得到一個與D相同類分布的合成數(shù)據(jù)集Dsyn；

步驟2：基于Dsyn，使用分類學習算法L訓練得到分類模型M；

步驟3：使用M對D中的少數(shù)類樣本集S分類，得到少數(shù)類樣本的分類難度；

步驟4：重復以上步驟nc次，將少數(shù)類樣本的nc次分類難度的平均值作為其最終的分類難度CD；

步驟5：將獲得的難度CD轉換為過采樣權重分布W；

步驟6：執(zhí)行下面過程，為少數(shù)類生成合成樣本數(shù)據(jù)集Syn。

（1）從S中根據(jù)過采樣權重分布W，抽樣出一個少數(shù)類樣本xi作為主種子樣本；

（2）從xi的k最近同類鄰居中隨機選擇一個少數(shù)類樣本xj作為輔助種子樣本；

（3）基于xi和xj，插值得到一個合成樣本，其中δ是一個元素處在［0，1］之間的隨機向量，“.*”代表元素級的乘法；

（4）將xs加入；

（5）重復（1）至（4）ns次，返回Syn。

步驟1與步驟2的目的是生成D的一個副本數(shù)據(jù)集Dsyn以訓練得到分類模型M，然后使用M去對少數(shù)類樣本集S分類。步驟3中，一個少數(shù)類樣本xi的分類難度可表示為：

其中yi是xi的真實標簽。即為預測xi時產生的軟損失。損失越高代表xi越難被M正確分類。由于Dsyn是使用SMOTE生成的原始數(shù)據(jù)集D的副本，其樣本受SMOTE中隨機因素的影響而具有一定的隨機性。步驟4的目的是為D生成多次的副本Dsyn，通過反復訓練與預測S，從而得到S中每一個樣本的可靠分類難度估計CD（一個少數(shù)樣本的最終分類難度是nc次估計的平均值）。

得到少數(shù)類樣本的分類困難度后，在步驟5中利用下面兩式將其轉換為一個過采樣權重分布W：

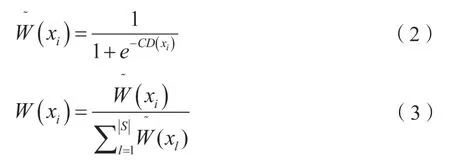
最后，基于W和S，在步驟6中為少數(shù)類生成合成樣本集Syn。步驟6中，每一個主種子樣本xi是據(jù)分布W從S中抽樣得到，越高分類難度的少數(shù)類樣本有越高的概率被選擇作為主種子樣本，從而有越大可能在其附近生成較多的合成樣本。

3 仿真實驗

3.1 實驗設置

3.1.1 數(shù)據(jù)集

我們從UCI數(shù)據(jù)庫［19］中選擇了18個現(xiàn)實的數(shù)據(jù)集作為實驗數(shù)據(jù)。這些數(shù)據(jù)集的特征總結如表1所示。從表1中可以看出，選擇的實驗數(shù)據(jù)集具有不同的特征數(shù)目、樣本數(shù)目和類不平衡度。

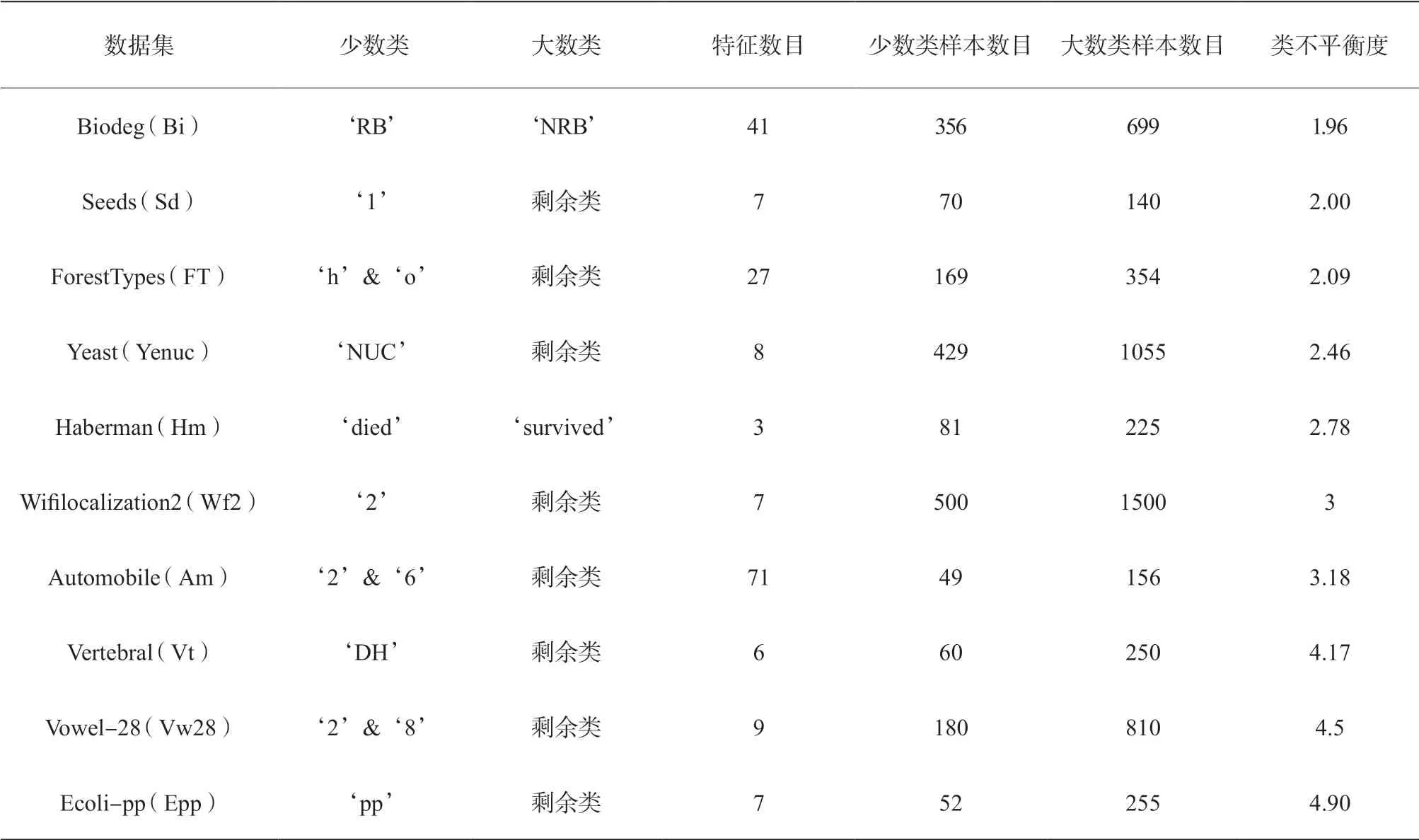
表1 實驗的18個UCI不平衡數(shù)據(jù)集的特征總結

續(xù)表

3.1.2 方法比較

在已有的文獻中，過采樣算法ADASYN、MWMOTE和GDO采用的權重計算方法分別是三種代表性的過采樣度權重分配方法。我們重點與此三種方法進行比較。為了剔除合成樣本生成方式的不同所造成的實驗干擾，將ADASYN、MWMOTE和GDO中的過采樣度權重方式分別與SMOTE的合成樣本生成方法相結合，簡寫為ADSM，MW-SM和GD-SM。此外，我們將被普遍采用的均勻權重分配方式也納入實驗比較中，即原始的SMOTE（簡寫為SM）過采樣。所有比較的方法的參數(shù)分別使用相應論文中的推薦值。實驗提出的CD-SM中，估計分類難度的次數(shù)nc設置為5。

3.1.3 性能指標

由于類分布的不平衡，評估分類模型在不平衡數(shù)據(jù)上的學習性能需要采用專門的類不平衡評價指標。在現(xiàn)有的研究中，F(xiàn)1、G-mean和AUC［12］是三個最為常用的面向類不平衡的性能指標。對F1、G-mean的定義如下：

其中，召回率Recall和精確度Precision分別是少數(shù)類樣本被正確預測的比率（即少數(shù)類的預測精度）和預測為少數(shù)類的樣本中實際為少數(shù)類的比率。不同于F1和G-mean，AUC不依賴于具體的決策閾值。實驗中每一個作為比較的方法在每一個數(shù)據(jù)集取得的實驗結果都基于10次獨立運行的5分層交叉驗證，然后將其平均值作為最后的性能。

3.1.4 統(tǒng)計性檢驗

Wilcoxon符號秩檢驗［20］是最受歡迎的非參數(shù)顯著性檢驗方法。我們使用此方法去驗證提出的方法與其他比較的方法間是否存在顯著性差異。

3.1.5 基分類器

我們使用一個三層的神經網絡作為基分類器，其輸入層和輸出層的神經元個數(shù)分別為訓練集的特征數(shù)目和類別數(shù)目，中間層采用固定的10個神經元。神經網絡以0.01的學習率訓練500代以收斂分類模型。

3.2 實驗結果與分析

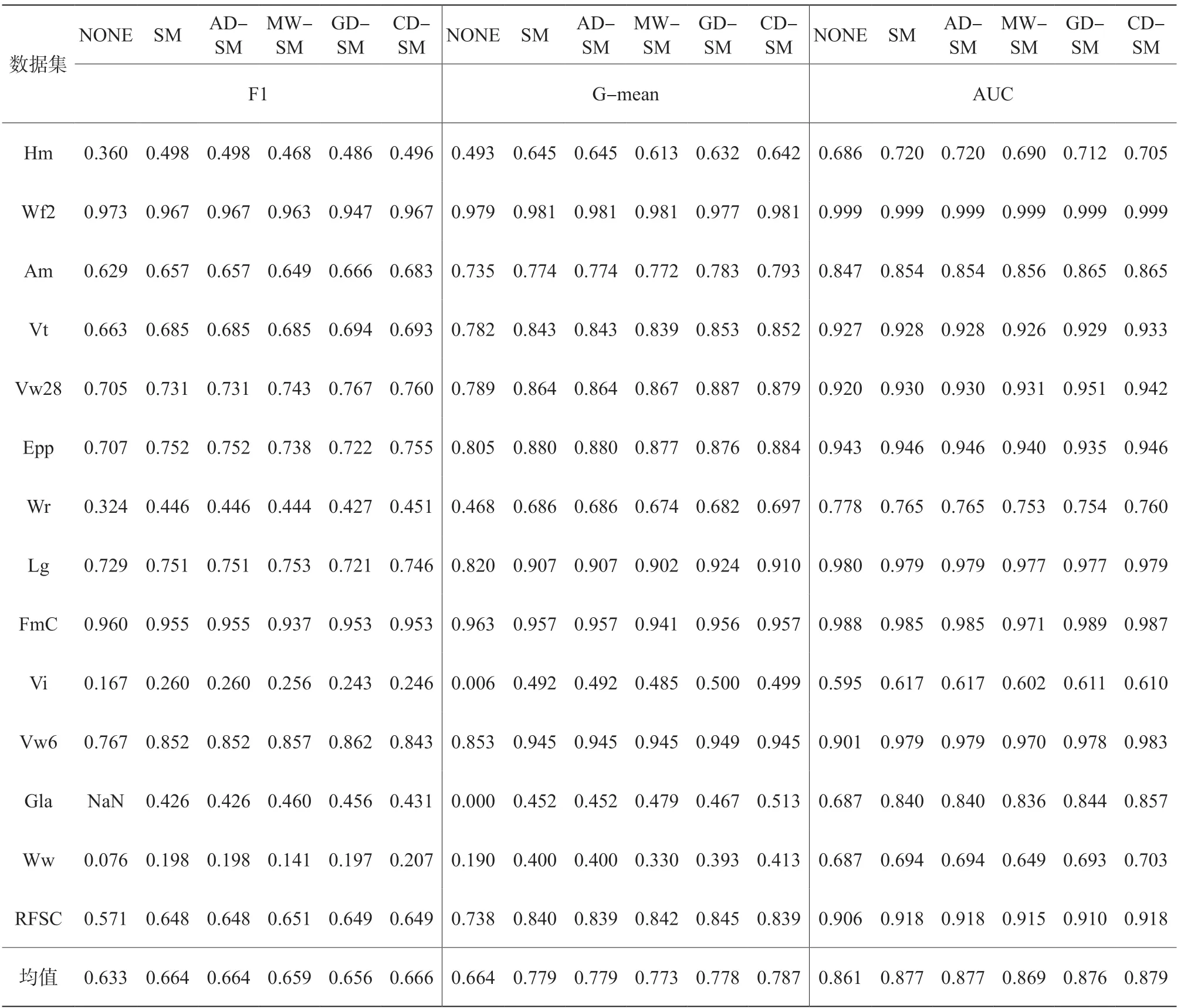
表2和表3分別總結了當過采樣倍率為100%和300%時，NONE、SM、AD-SM、MW-SM、GD-SM和我們提出的CD-SM在每一個數(shù)據(jù)集上的F1、G-mean和AUC性能值（NONE表示未結合任何過采樣算法的性能結果）。基于表2和表3的結果，CD-SM在兩種過采樣倍率和每一種評價指標下都獲得了最好的平均性能值。為更好地演示各種比較的方法的競爭力，圖1給出了所有用于比較的方法在18個實驗數(shù)據(jù)集上的平均性能排名。從圖1可以看出，CD-SM以明顯的優(yōu)勢在每一個評價指標上獲得最低的平均排名，表明基于分類難度的過采樣權重分配方法具有最高的競爭力和穩(wěn)健性。

圖1 a與b分別表示當過采樣倍率100%和300%時，各方法在F1、G-mean和AUC上的平均排名

表2 過采樣倍率100%時，比較的方法在18個實驗數(shù)據(jù)集上的F1、G-mean和AUC性能結果

表3 過采樣倍率300%時，比較的方法在18個實驗數(shù)據(jù)集上的F1、G-mean和AUC性能結果

續(xù)表

為了測試比較的方法間是否存在顯著性差異，表4列出了CD-SM與其他每一個方法的Wilcoxon符號秩檢驗結果（“++”“+*”分別表示CD-SM以0.05和0.1的顯著性水平好于其他比較的方法，“+”表示CD-SM只定量地好于其他比較的方法）。表4的結果說明在絕大部分情況下，CD-SM顯著性地好于其他比較的方法，從而驗證了提出的方法的有效性。

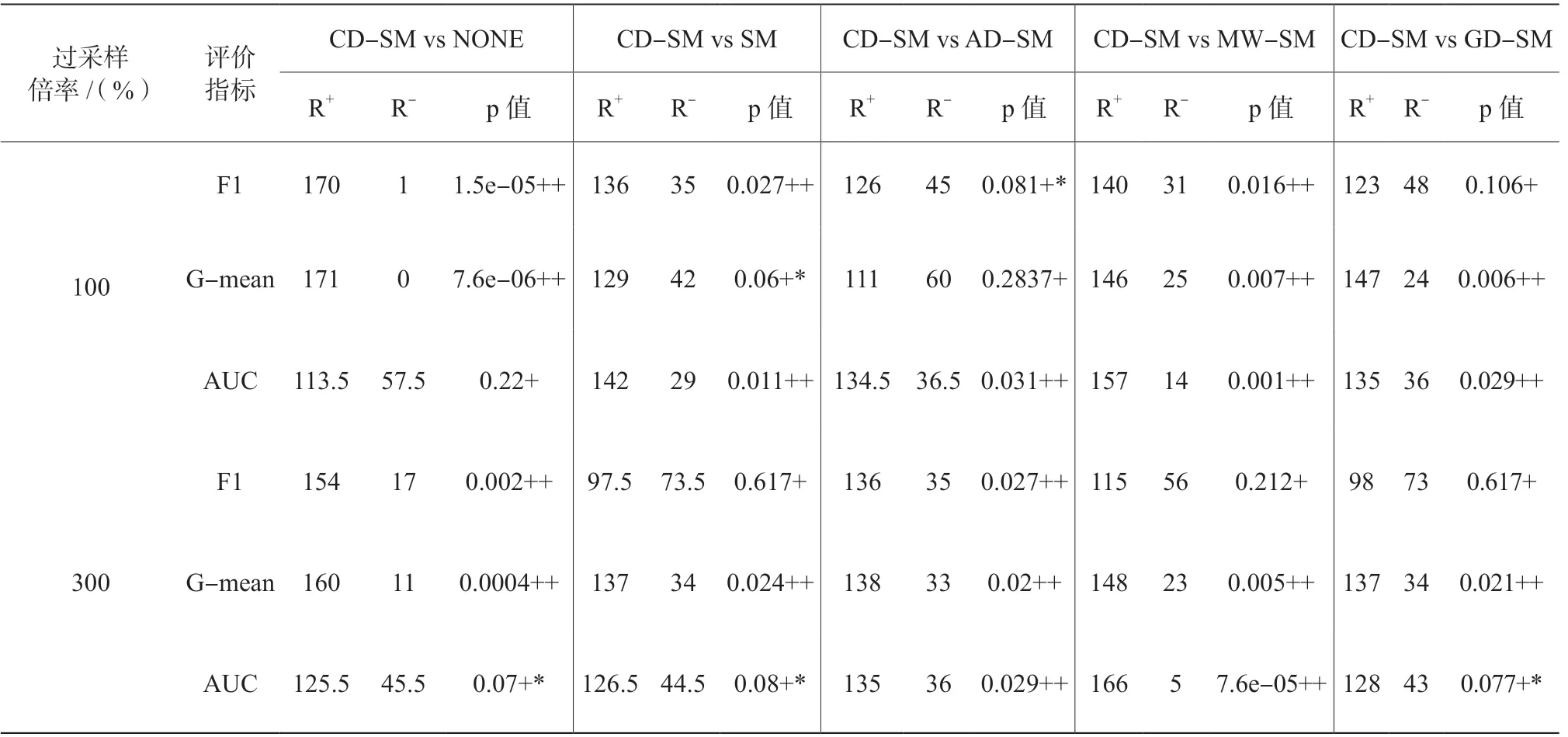
表4 CD-SM與每一個其他比較的方法間的Wilcoxon符號秩顯著性檢驗結果

4 結論

我們提出了一種基于分類難度的加權過采樣方法，將分類學習算法在少數(shù)類樣本上的分類損失作為過采樣權重，以強化那些難于正確分類的少數(shù)類樣本的學習。不同于已有的加權過采樣方法，我們提出的方法分配過采樣權重不再基于數(shù)據(jù)特征所反映的樣本重要性，而是直接考慮當前的分類學習算法對少數(shù)類樣本的分類難度。為了評價提出的方法的有效性，我們以18個UCI現(xiàn)實數(shù)據(jù)集為實驗數(shù)據(jù)，以神經網絡為基分類器進行實驗，結果表明，此方法在常用的評價指標F1、G-mean和AUC上都優(yōu)于現(xiàn)有的加權過采樣方法。

最后，需要指出的是，我們提出的方法需要額外訓練nc次的模型和預測nc次的少數(shù)類樣本集去獲得準確的分類難度分布。在實驗仿真中，CD-SM的nc只需設置為一個較小的常數(shù)5，即可取得相比已有方法顯著更好的性能。因此，我們認為其產生的額外時間代價是值得的。