基于分區FA-MLP-CA模型的城市擴張模擬
——以成渝地區雙城經濟圈為例

李 婷，劉 明 皓，陳 春，李 俊 儀

(1.重慶郵電大學計算機科學與技術學院/重慶郵電大學空間信息研究中心，重慶 400065；2.重慶交通大學建筑與城市規劃學院/重慶交通大學生態人居與綠色交通研究中心，重慶 400074)

0 引言

元胞自動機(Cellular Automata，CA)是模擬城市土地利用變化的有效工具，其核心問題是如何有效提取最佳的用地轉換規則[1]。在城鄉CA動態建模過程中，鄰域和局部莫蘭指數(Local Moran′sI)已被很好地用于表達事物的空間相互依賴[2,3]，然而，如何引入空間異質性用于提取用地轉換規則是學術界一直探討的熱點問題[4-7]。空間異質性作為空間地物的固有特性，指因地理位置和時間變化而引起的變量間關系或結構的變化，主要表現為時空非平穩性。城市用地擴張及其驅動因子之間表現為強烈的時空非平穩性，通過CA建模的方式可深入揭示這一特性，有助于更好地理解城市變化的動態過程[8,9]。與機理模型不同，由數據驅動的城市用地動態變化CA模型是通過尋找驅動因子與城市用地變化之間的相關關系獲得用地轉換規則，常用方法有Logistic回歸[10,11]、神經網絡[12-14]、遺傳算法[15,16]和蟻群算法[17]等。這些方法能較好地揭示城市擴張的全局特征，但對局部特征的探究非常有限。

為更好地反映城市擴張變化的時空異質性規律，不同方法被引入城市用地變化建模中，其主要思路有兩種：1) 在常用回歸模型基礎上引入位置的權重矩陣和時間特征解決城鎮用地擴展的時空非平穩性問題，如地理加權模型或時空地理加權模型[18-21]。2) 在建模過程中采取分區建模方式，其中，如何分區、度量和篩選驅動因子成為研究重點,目前已有眾多方法[22]：一是借助已有分區邊界(如行政區、經濟區等)進行疊置分析，形成更多子區域[23]，這類分區方法多是經驗基礎上的分區，主觀性較強；二是對驅動因子進行熱點探測，將待模擬城市的全部元胞按其距某因子的距離分為重要影響區域和一般影響區域，對N個影響因子所劃區域進行疊加，理論上可分為2N個元胞狀態區域[24,25]，這種分區方法會因驅動因子數量的增加而變得十分復雜；三是根據相似性原理采用K-means、SOM等算法進行分區[26,27]，多基于屬性相似性進行計算，而作為因變量的建設用地擴張速率明顯反作用于城市擴張發展，并有效體現出城市區域差異，這種分區方法相對客觀，同時避免了眾多的元胞狀態分區。另外，在分區建模過程中，如何篩選和優化因子以提升模型運行效率和增強因子的可解釋性也需進一步探討。因子分析(Factor Analysis，FA)方法是常用的評價方法[28-30]，但在城市擴張中少有運用。已有研究表明，多層感知機(Multi-Layer Perceptron，MLP)的耦合模型能有效優化目標函數，提高模型準確率[31]，適用于體量大、非線性特征明顯的數據。如徐廣才等結合MLP與Markov模型分析各土地利用類型的轉換潛力，發現該耦合模型可以非常有效地預測驅動力穩定時土地利用的變化趨勢[32]；林江構建MLP-CA-Markov模型對晉江市的土地利用進行模擬，研究表明人工神經網絡具有獲取模型參數和處理非線性數據復雜關系的能力[33]。綜上，本研究采取分區建模方式，引入城市擴張速率優化傳統的K-means屬性分區，同時采用FA方法耦合MLP與CA，構建基于城市擴張速率分區的FA-MLP-CA模型，以提升空異質性建模精度，改善驅動因子的可解釋性。

1 研究區域與數據

1.1 研究區域

自2011年《成渝經濟區區域規劃》和2016年《成渝城市群發展規劃》發布以來，成渝地區雙城經濟圈(以下簡稱“成渝圈”)的城市發展備受關注。成渝圈位于長江上游，包括四川省的15個市和重慶市的27個區縣，總面積18.5萬km2，是中國西部高質量發展的重要增長極和帶動我國西部發展的重要區域(圖1)。2020年中共中央政治局指出，推動成渝圈建設，是構建以國內大循環為主體、國內國際雙循環相互促進的新發展格局的重大戰略舉措。然而，由于自然、社會、政策等因素長期影響，該區域內部城市群空間格局差異較大[34]，空間異質性明顯控制著該區域城市空間格局特征以及不同區域城市發展的速度，有必要采取分區建模，以提高該區域城市模擬精度，為成渝地區高質量發展提供決策支持。

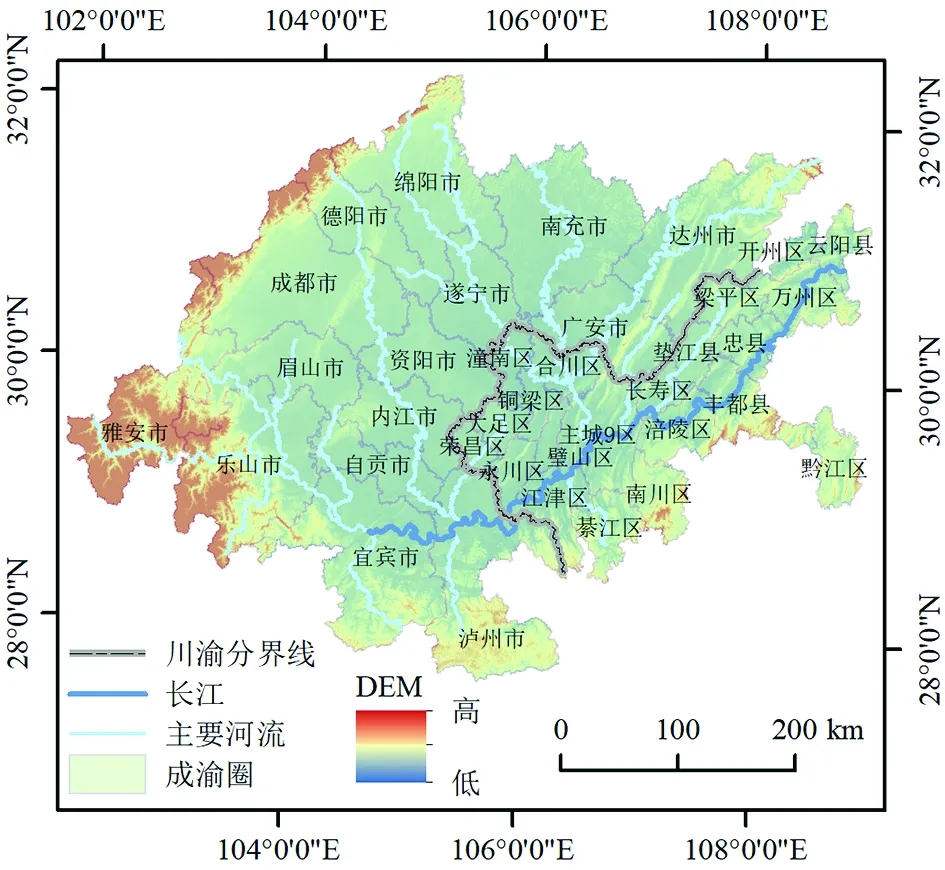
圖1 成渝地區雙城經濟圈行政區劃Fig.1 Administrative area of Chengdu-Chongqing economic circle

1.2 數據來源與處理

考慮到四川的盆地地形和重慶的山地地形，以及成都和重慶兩大核心城市與其他城市的發展差距，本研究選用自然因素和社會因素作為城市擴張的驅動因素。如表1所示，土地利用數據來源于全球30 m地表數據集(GLOBELAND30)，DEM數據來源于地理空間數據云，夜間燈光數據來源于NOAA國家環境信息中心(NOAA′s National Centers for Environmental Information)，路網數據包括鐵路、高速公路和河流數據，來源于OpenStreetMap；POI數據包括機場、火車站、政府機關、商場和學校等點要素數據，其中機關指市級政府機關和區級政府機關，學校包括大、中、小學，通過爬蟲獲取。所有數據經過重分類統一分辨率為200 m，將路網數據和點數據進行歐氏距離分析和點密度分析，構建包含11個驅動因子的數據集(圖2)。

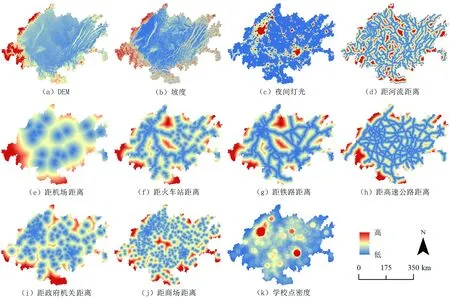
圖2 驅動因子數據Fig.2 Data of driving factors

表1 研究數據Table 1 Research data

2 模型構建與研究方法

2.1 基于城市擴張速率分區的FA-MLP-CA模型

FA-MLP-CA模型的模擬流程(圖3)為：1)以區縣為基本單元，檢測基期年和末期年建設用地數據，得到各區縣城市擴張速率統計數據；2)利用K-means算法對城市擴張速率統計數據和驅動因子數據進行空間聚類，得到分區聚類結果；3)將驅動因子數據結合聚類分區結果按不同區域分別進行因子分析優化；4)將優化后的因子和建設用地變化數據分區抽樣后輸入MLP模型進行訓練，并得到各區域內每個元胞的轉換適宜性圖層；5)根據城市發展適宜性、鄰域效應和限制因素計算得到各區域的總體轉換概率；6)根據建設用地變化數據統計得到各分區建設用地變化總量，作為各區域CA模型的迭代終止條件；7)對不同區域的模擬結果匯總后進行精度評估，若滿足要求，則輸出模擬結果，反之，調整模型參數，繼續模擬。

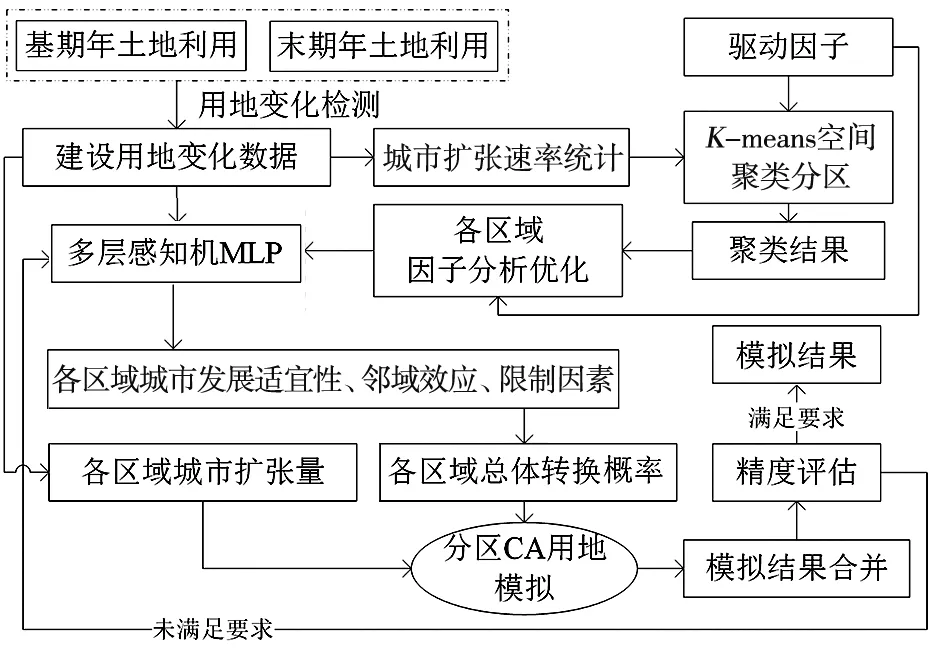
圖3 基于城市擴張速率分區的FA-MLP-CA模型技術路線Fig.3 Technical route of FA-MLP-CA model based on urban expansion rate zoning

2.2 空間聚類分區

空間異質性是地理事物與現象在空間上表現出來的一種固有屬性，對研究區進行分區建模，通過分區學習用地轉換規則，可減小機器學習模型因空間異質性導致的對局部特征學習不充分問題，從而提高模擬精度。已有研究多以驅動因子的空間相似性進行分區，此外，城市擴張速率可直觀表達區域內城市擴張發展的速度，具有時間和空間特性，作為變化結果之一，是實驗研究的有效參考依據，故本文采用驅動因子相似性和城市擴張速率的雙約束方式，利用K-means算法對研究區域進行空間聚類分區，其思想是同一空間(簇)內的對象相似度較高，反之則較低。該算法實現步驟為：1)采用離簇中心最遠的原則從數據集中選擇K個點作為簇中心(初始質心)，即離已存在的簇中心距離越遠的點被選為下一個簇中心的概率越高；2)計算所有數據點距所有簇中心的距離，并將其劃分到距離最近的簇；3)重新計算各簇的中心點，將該點作為新的簇中心；4)重復步驟2)和步驟3)，直至所有的簇中心點不再發生移動。

2.3 因子分析

因子分析通過研究變量相關系數矩陣內部的依存關系，對高維度的因子進行分析得到低維度的新因子，其計算公式見式(1)，具體可表示為式(2)。進行因子分析后，可得到各驅動因子的方差貢獻率和累計方差貢獻率，以各驅動因子的方差貢獻率除以累計方差貢獻率即可求得各驅動因子的權重。

X=AF+E

(1)

式中：A為因子載荷矩陣；F為主因子，即新的因子；E為特殊因子。該模型可具體表示為：

Xi=∑aijFj+εi

(2)

式中：Xi為原始變量(i=1,2,…,n,n為變量數)；Fj為公共因子，即新因子(j=1,2，…，m,m為公共因子數)；aij為第i個變量與第j個公共因子之間的相互關系，即因子載荷；εi為Xi的特殊因子。

2.4 轉換規則提取

CA模型中，元胞的總體轉換概率通常由城市發展適宜性、鄰域效應和限制因素決定。本研究采用在非線性數據上有較優表現的多層感知機模型(MLP)提取轉換規則，該模型的網絡結構包含輸入層、隱藏層和輸出層，其隱藏層可為一層或多層，使模型具有較強的自適應和容錯能力，輸入層由各分區的因子數量決定，輸入層將數據逐層傳輸到隱藏層，最后到輸出層。使用隨機采樣方法選取70%的數據作為樣本數據集，30%的數據用于訓練模型網絡參數以及驗證模型精度并得到最優的變量權重和偏置量參數；預測階段將各驅動因子和模型網絡參數導入訓練好的模型，計算得到每個元胞在下一時刻轉換為建設用地的概率Pc(i,t)。隱藏層第j個神經元所接收到的信號可表示為：

netj(i,t)=∑ω(i,j)xi(k,t)+bj(k,t)

(3)

式中：ωi,j為輸入層和隱藏層間的權重值；xi(k,t)為t時刻第j個神經元從像元k接收到的信號；bi(k,t)為偏置值。

鄰域效應指摩爾鄰域內中心元胞與周圍元胞的相互作用，則元胞i在t時刻的鄰域效應可表示為：

(4)

式中：S(i,t)為元胞i在t時刻的狀態；con()為條件函數，當元胞狀態為建設用地時，值為1，否則為0。

考慮到地理和政策因素，某些土地利用類型不能轉換為建設用地[35]，即限制因素，可表示為：

Pl(i,t,k)=con(S(i,t)=Landusek)

(5)

式中：Landusek為第k種土地利用類型；當元胞i在t時刻為第k種土地利用時，條件函數con()的值為0，否則為1。考慮到走生態文明建設道路是成渝圈未來發展的必然選擇，故設置水域、部分森林等為限制因素，使2020年水域和森林不轉換為建設用地。

綜上，在建設用地擴張的過程中，元胞i在t時刻轉換為建設用地的概率P(i,t)為：

P(i,t)=Pc(i,t)×Ω(i,t)×Pl(i,t,k)

(6)

2.5 實驗方案設計

本文設計3組對比試驗：1)是否對研究區域進行K-means分區建模，以檢驗分區模擬的有效性；2)是否引入城市擴張速率作為K-means分區建模的條件，以檢驗城市擴張速率在分區模擬中的作用；3)在引入城市擴張速率進行K-means分區的基礎上，是否進行因子優化建模，以確定不同分區內最佳驅動因子組合。

2.6 精度檢驗

本文研究區空間異質性明顯，用總體精度(OA)和Kappa系數進行檢驗具有局限性，故采用品質因數(FoM)(式(7))進行一致性檢驗，其更適用于復雜地理系統模擬的一致性和準確性檢驗[36]。

FoM=B/(A+B+C+D)

(7)

式中：A為實際發生轉換，但模擬中未發生轉換的區域面積；B為實際和模擬均發生轉換的區域面積；C為實際和模擬均發生轉換，但轉換為與實際不相同的區域面積，本實驗中只涉及非建設用地轉換為建設用地，故C=0；D為實際未發生轉換，但模擬中發生轉換的區域面積。

3 結果分析

3.1 驅動因子選取

由2010年和2020年土地利用數據得到以區縣為統計單位的城市擴張速率柵格數據；將該數據同處理好的驅動因子進行K-means聚類分析，將研究區域劃分為3個子區域(圖4)，可直觀發現引入城市擴張速率后劃分的區域更細化，同區域內的柵格數據相似性更高。通過因子分析對子區域分別進行因子優化，以因子累計貢獻率大于85%為選擇標準，得到3個子區域的適宜因子數量分別為8、8、7(圖5)。將各區域驅動因子排序(圖6)，分別從中選擇前8、8、7個驅動因子作為MLP模型的輸入數據。

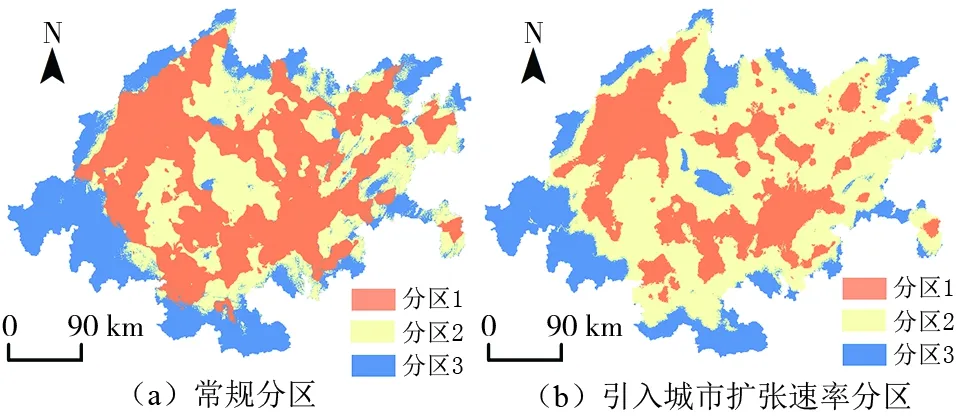
圖4 K-means聚類分區結果Fig.4 Zoning results based on K-means clustering

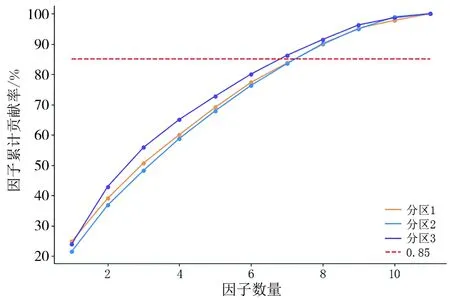
圖5 因子分析結果Fig.5 Results of factor analysis

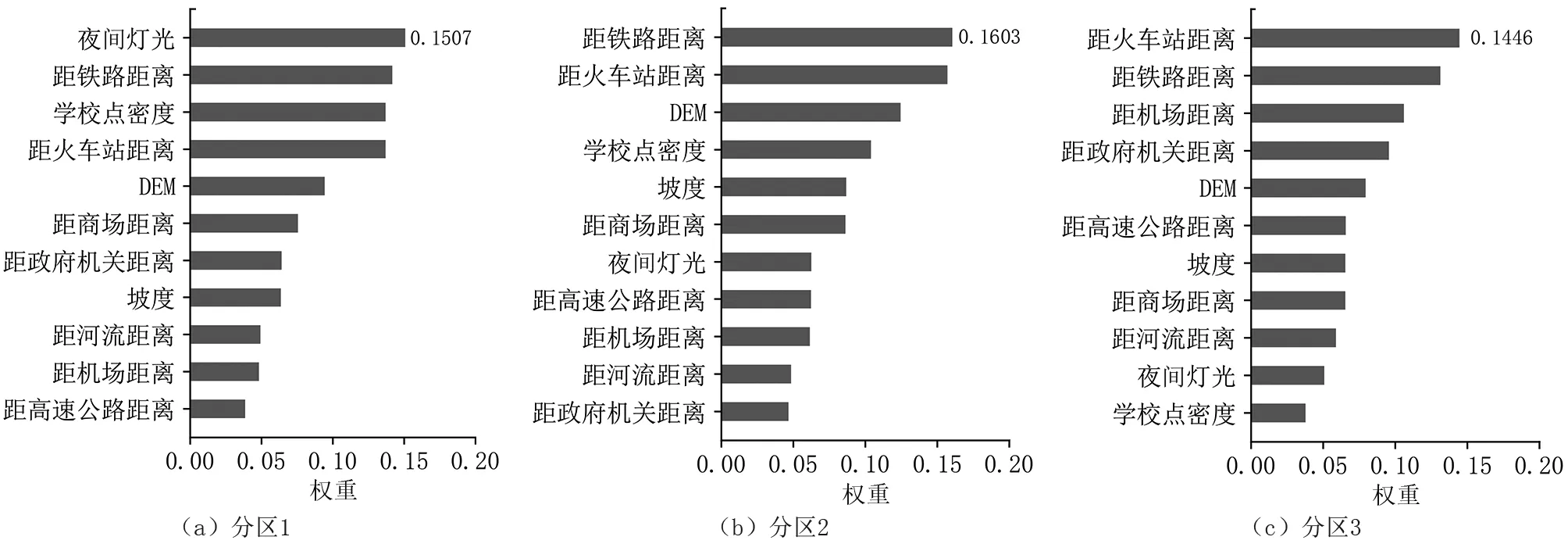
圖6 各區域驅動因子權重排序Fig.6 Ranking of driving factors sorted by weight in each region

3.2 精度評價與城市擴張模擬結果

以2010年成渝圈城市用地為初始狀態，通過分區和因子分析方法模擬得到2020年城市擴張結果，并與2020年實際城市用地分布進行對比(表2)。可以看出，傳統的MLP-CA模型的3項精度指標均優于未來土地利用變化情景模擬模型(GeoSOS-FLUS)，說明MLP-CA模型在城市擴張模擬中具有較好的實用性；常規分區MLP-CA模擬的結果比未分區模擬的FoM和OA分別提高0.0694和0.0033，說明對研究區域使用K-means進行分區模擬，能在一定程度上反映空間異質性規律，從而提高模型模擬精度；城市擴張速率分區MLP-CA模擬的結果比未引入城市擴張速率的常規分區MLP-CA模擬的FoM和OA分別提高0.0207和0.0029，說明考慮不同行政區的空間發展差異能改善城市擴張模擬效果，更符合城市動態變化規律；進行因子優化的城市擴張速率分區FA-MLP-CA比城市擴張速率分區MLP-CA模擬的FoM和OA分別提高0.0091和0.0014，說明考慮驅動因子對建設用地擴張的影響程度及其最佳因子組合可在一定程度上提高模擬精度。

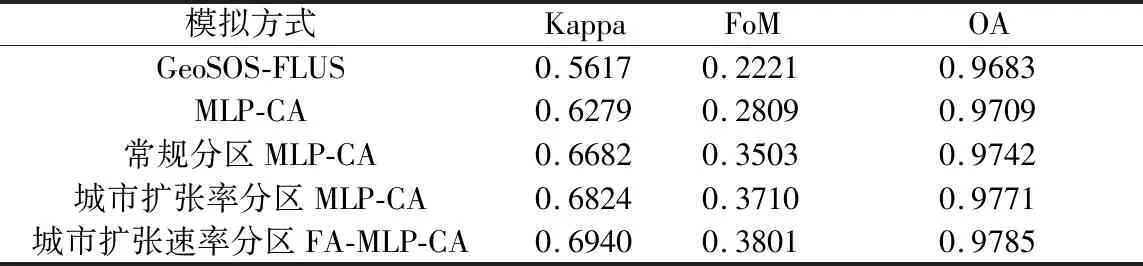
表2 模擬精度對比Table 2 Comparison of simulation accuracy

綜上，在無分區模擬中，驅動因子在城市密集的中心區域表達更好，城市用地擴張變化效果較好，而城市較分散地區在模擬過程中很難揭示驅動因子特征，因此模擬效果較差(圖7b)。在分區模擬中，模型能充分揭示不同區域的特征，較客觀反映城市擴張的空間異質性規律，故能較好地模擬各區域內的城市擴張情況(圖7c-圖7e)；引入城市擴張速率且加入因子分析優化，可對驅動因子進行數據降維，使對驅動因子的探究達到最佳(表2，圖7d、圖7e)。

3.3 因子重要性分析

如圖8所示，不同驅動因子對不同分區城市擴張變化的影響力大小不同。分區1主要分布在城市密集區域，代表城市發展高度適宜區，城市發展水平較高，其權重最高的因子為夜間燈光，權重達到0.1507，鐵路、火車站等交通因素以及學校對其城市擴張的影響較大；分區2主要分布在城鄉過渡和交接地帶，代表城市發展中適宜區，主要為中小城鎮，其權重最高的因子為距鐵路距離，權重達0.1603，該區域城市發展對城市基礎建設(如火車站、鐵路、學校、商場等)的依賴相對較高；分區3主要為現有城市較偏遠區域，代表城市發展低適宜區，其權重最高的因子為距火車站距離，權重達0.1446，對驅動因子的依賴與分區2相似但也有一定差異。

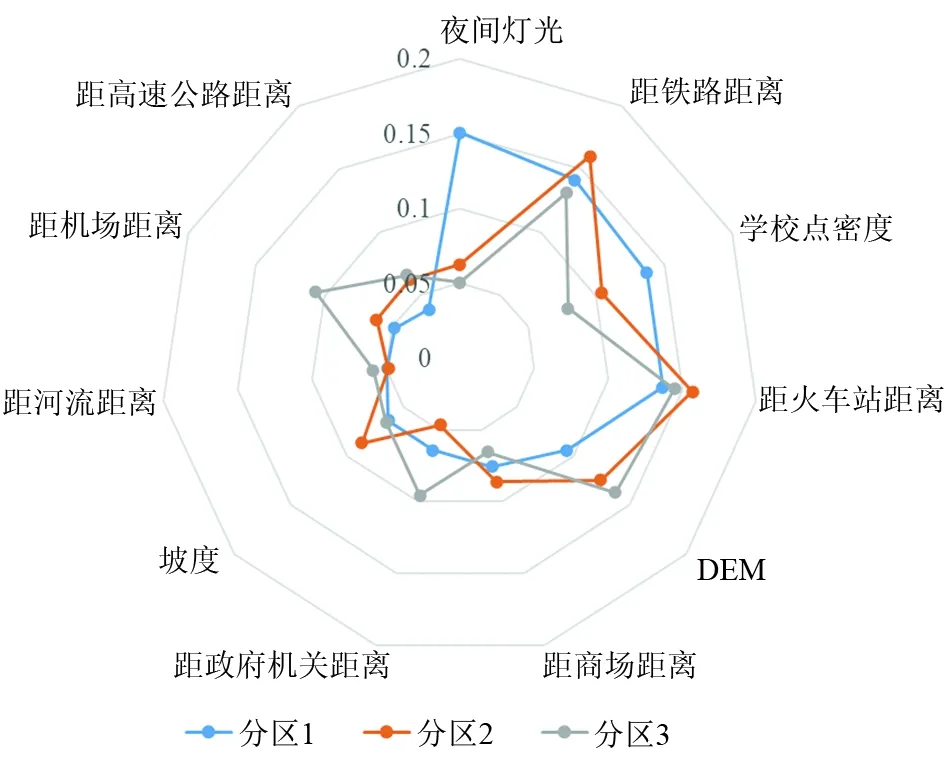
圖8 驅動因子影響力的分區差異Fig.8 Regional differences in the influence of driving factors

從驅動因子的影響力變化看，分區2和分區3的差異不明顯，表現在驅動因子影響力(權重值)的一致性較高；但分區1和分區2、3差異明顯，表現在驅動因子影響力(權重值)差異較大。值得一提的是，在各驅動因子的影響中，學校點密度和夜間燈光兩個因子對城市擴張的影響表現出強烈的空間異質性。學校點密度的分區差異與城市的發展趨勢相呼應，學校分布越多的區域，居民住房需求越大；夜間燈光也從側面表現了分區1的城市發展水平。上述因子分析從不同側面證明了進行分區建模的必要性。

3.4 未來城市擴張預測

根據成渝圈2010-2020年建設用地變化數據，使用馬爾科夫鏈計算得到2020-2030年的建設用地擴張量為172 969個柵格，并以2020年建設用地的模擬結果為初始狀態，通過城市擴張速率分區FA-MLP-CA模型預測2030年建設用地擴張結果(圖9)。結果顯示，成渝圈內的城市仍以成都市和重慶主城區等為核心區域向外擴張發展，且有連點成線、連區成片的趨勢，未來成渝圈的發展戰略必將進一步強化這兩種趨勢。

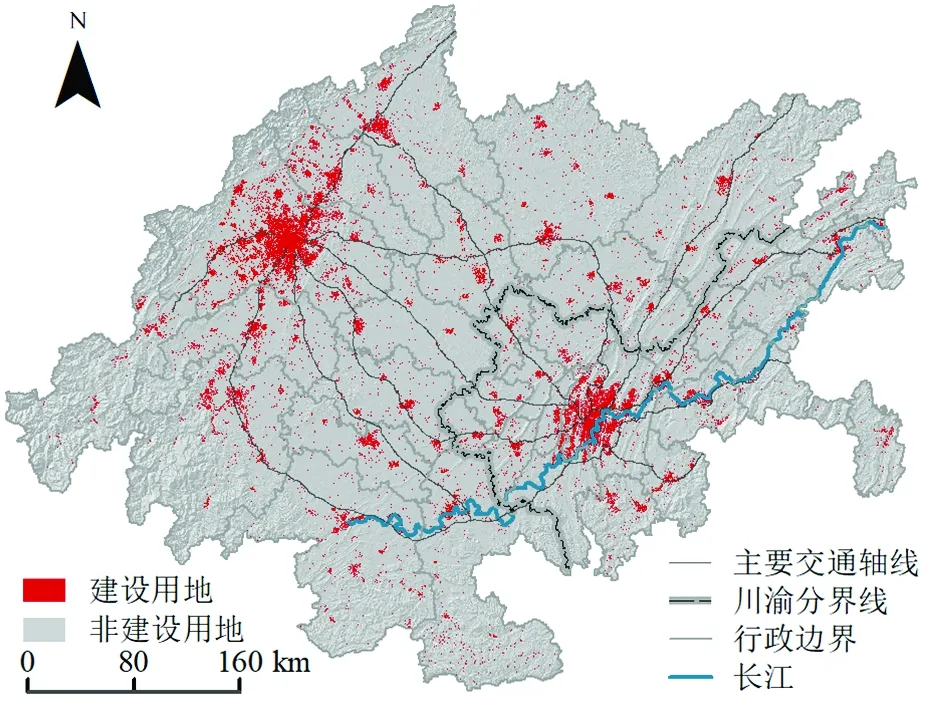
圖9 2030年成渝圈城市擴張模擬Fig.9 Simulation of urban expansion in Chengdu-Chongqing economic circle in 2030

4 結論

本文構建基于城市擴張速率分區的FA-MLP-CA模型，以成渝圈2010年建設用地數據作為初始狀態，通過對不同區域內城市擴張的內在規律挖取不同的轉換規則，得到成渝圈2010-2020年的城市擴張適宜性，并模擬得到成渝圈2020年的城市擴張模擬結果；通過消融試驗(未分區模型、未引入城市擴張速率和未引入因子分析優化模型)比較和因子分析，驗證了模型的可行性和分區建模的必要性；最后使用城市擴張速率分區FA-MLP-CA模型對成渝圈2030年的城市擴張進行預測模擬。研究結果表明：1)對于較大范圍的研究區域，可對其進行分區建模，通過挖掘不同分區內的不同轉換規則，能改善常規機器學習建模過程中因空間異質性導致的對局部特征學習不充分的問題，從而有效提高模型的模擬精度；2)在分區建模過程中，可考慮驅動因子在自然地理要素(高程、坡度等)的相似性、經濟區位的相似性(如道路、學校、行政中心距離等基礎設施的影響)，還可考慮經濟發展環境的相似性(如基于城市擴張速率的分區對城市擴張模擬精度的影響)，從而有效提高模擬精度，改善模擬結果；3)對驅動因子進行因子分析可獲得因子重要性權重，據此對各子區域驅動因子進行差異化選擇，既可增強因子的可解釋性，又可提升模型的運行效率，在一定程度上彌補因分區導致的計算效率降低問題；4)成渝圈未來的城市擴張特點是以成都市和重慶主城區兩大都市為核心，向外圍城市軸向擴散、連點成線、連區成片的趨勢。

空間異質性是地理事物的固有屬性，因地制宜是城市空間決策的重要指導思想。K-means聚類分區是非監督學習的城市發展適宜性評價的方法，與從先驗知識出發的常規城市發展適宜性評價(如GIS疊置等分析)方法相比，該方法更客觀高效；而引入城市擴張速率的分區建模思想既考慮了驅動因子在自然要素的地理相似性，也考慮了經濟發展環境的地理相似性，能更好地反映城市發展演變規律。因子分析與聚類分區相結合，為量化地理現象驅動因子的空間差異提供了重要方法和手段，其與表示事物空間異質性的定量指標(如Moran′sI指數等)結合，既可度量事物空間異質性，還能有效揭示事物發展演變的內在機理。本文使用分區建模的方式對城市擴張過程中空間異質性的影響進行了度量，而城市擴張在不同時間段呈現出差異性，因此時間異步性對城市擴張也有一定影響，但本文未考慮該影響，有待后續研究。