具有階段結構種群模型的局部穩定性分析

于倩

(吉林師范大學 吉林長春 130000)

廣義系統又可以叫作奇異系統，該系統理論的產生，已經被諸多領域廣泛應用，比如電路系統理論、經濟學系統理論、航天工程系統理論等。近年來，很多學者用廣義系統理論來研究多種生物種群動力系統。文獻[1]研究了具有階段結構的食餌——捕食者系統以及具有階段結構的單種群模型系統，并分析了系統在平衡點附近的是否具有穩定性。文獻[2-5]研究了具有階段結構的廣義食餌—捕食者系統，在這些文獻中所建立的系統，有考慮到食餌的幼年和成年的問題，也有考慮到捕食者的幼年和成年的問題，同樣的，也分析了系統在正平衡點附近的局部動態行為。

該文將繼續研究具有階段結構的廣義食餌——捕食者系統。在該文中，系統中對于食餌和捕食者而言，考慮到了食餌的幼年和成年的問題，且捕食者僅捕獲成年的食餌。為了后續研究捕獲行為產生的經濟效益問題系統中也將對捕食者進行捕獲的經濟因素考慮在內。

1 預備知識

引理1 勞斯-霍爾維茨判據[6]若系統的特征方程為

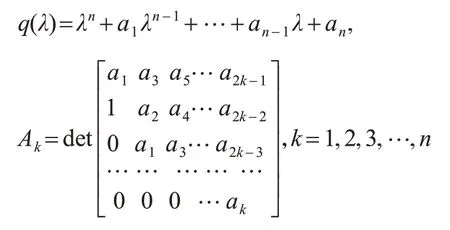
其中，當k＞n時有ak=0，則q(λ)=0 根的實部均為負的充要條件是Ak＞0并且ak＞0。

引理2（奇異誘導分岔定理[7]）對于廣義系統

其中，x為n維系統變量，y為m維系統變量，λ表示p維數的系統參數。令D表示微分算子，Δ=det(Dyg),如果該系統在(0,0,δ0)滿足下列條件。

（1）f(0,0,δ0)=0,g(0,0,δ0)=0,Dyg在(0,0,δ0)附 近有一個零特征值并且trace(Dyfadj(Dyg)Dxg) ≠0。

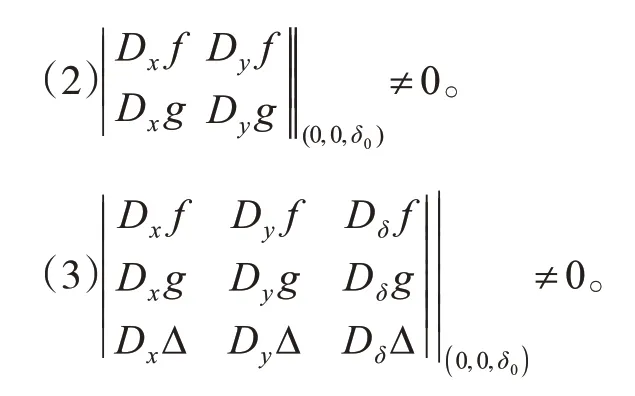
在Rn+m+1空間內，在系統式（1）的平衡點附近存在一個光滑曲面，該曲面通過并且與奇異曲面相切于(0,0,δ0)，系統式（1）在該平衡點附近出現奇異誘導分岔。

當δ增加通過δ0時，如果U/I＞0，那么系統式（1）在該平衡點的線性化矩陣的一個特征值從C-平面變化到C+平面，如果U/I＜0，那么系統式（1）在該平衡點的線性化矩陣的一個特征值從C+平面變化到C-平面；而系統式（1）其他特征值保持有界性并。其中

2 系統建立

假設該系統生存在一個特定的環境中，此環境中部分資源是有限的，而這部分資源又是系統內各種群生存的必要條件；又假定生物群體的生長不受季節的影響；再假定在任何時期內，對于具有階段結構的種群的種群密度，幼年種群與成年種群成正比，則食餌的內稟增長率為n，種群的死亡率與種群密度成比例，其中幼食餌種群的死亡比例系數為d1。成年食餌種群的死亡比例系數為d2，捕食者種群的死亡比例系數為d3；根據前面對于特定環境的假定，可以說明幼食餌種群內部存在競爭，同樣，捕食者種群內部也存在競爭，且種群的競爭行為和種群密度是成比例的，則令幼食餌的競爭比例系數為s1，捕食者的競爭比例系數為s2；該文對具有階段結構的種群進行研究，但只針對食餌種群的階段結構，還未考慮捕食者種群的階段結構因素，且僅對成年食餌進行捕獲，捕食率為m。上述提到的各個參數均為正的常數，w表示捕食者種群的市場單位價格，c表示捕獲捕食者所產生的單位成本，v表示捕獲捕食者所產生的經濟收益。

根據以上的假設，可以建立如下廣義種群系統模型。

該系統滿足如下初值條件：

其中，x1(t)與x2(t)分別表示幼年食餌種群密度與成年食餌種群密度，y(t)表示捕食者種群密度，E(t)表示捕食者種群的捕獲努力量。

根據H.S.Gordon 提出有關公共資源理論[8]，該理論中指出，當經濟利益為零時，系統會出現“生態經濟平衡”現象。在系統式（2）中，在正平衡點[9]處出現“生態經濟平衡”現象，此時，可求得

系統局部穩定性分析如下。

通過引理2，可令Δ=det(DEh)=wy(t) -c，通過簡單計算有

顯然，

通過以上的分析，可以整理得到以下4點：

（1）顯然f(0,0,0)=0,g(0,0,0)=0,DEh在正平衡點附近有一個零特征值且trace(DEfadj(DEh)DGh)|P*≠0。

（4）顯然可得

由以上內容可得引理2中的3個條件均可滿足，所以系統式（2）在正平衡點附近出現奇異誘導分岔，而且可以看出v等于0是分岔值。

經過簡單計算可以得到

所以，由引理2 可以得到，當v由小于0 增加到大于時0，如果U/I＞0，那么系統式（2）在該平衡點的線性化矩陣的一個特征值從C-平面變化到C+平面。

系統式（2）在正平衡點附近的線性化矩陣為

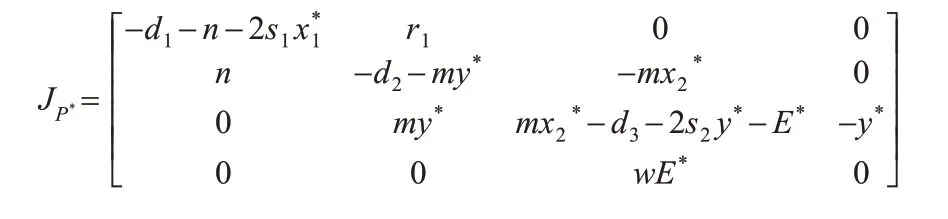
所以，系統式（2）在平衡點附近的特征方程為

由建立系統模型的條件以及式（3）可知，以下兩式成立

因此，根據引理1可以得知系統式（2）在正平衡點的線性化矩陣的其余兩個特征值λ2,λ3都具有負實部.又通過以上證明可知，當v由小于0 增加到大于0 時，只有特征值λ1從C-平面變化到C+平面，而λ2,λ3這兩個特征值一直處在在C-平面，并且他們的變化是連續且有界的，也就是說，只有λ1的變化對系統式（2）在正平衡點附近的穩定性有影響，而λ2,λ3不影響系統式（2）在正平衡點附近的穩定性。如表1中給出當v由負到正通過0時，λi(i=1,2,3)實部的變化情況。

表1 系統式（2）在正平衡點附近的線性化矩陣特征值實部符號

根據表1可以得出當v＜0時，系統式（2）在正平衡點附近穩定；當v＞0 時，系統式（2）在正平衡點附近不穩定[10,11]。

3 結語

上述證明結論表明，當v由小于0 增加到大于0時，系統式（2）正平衡點附近出現SIB分岔并且不具有穩定性，且分岔值為v=0。而SIB 分岔會導致脈沖現象，這可能會使模型系統式（2）崩潰，也就是說，當經濟利益為正時，會阻礙生態系統捕獲的可持續發展，因此為了使生物資源的可持續發展，應該在經濟上能夠獲取收益時，消除奇異誘導分岔引起的脈沖現象，使模型系統式（2）穩定，此部分內容將作為筆者的后續研究內容。