Rigidity about two linear structures on the space of measured laminations*

Department of Basic Courses，Guangzhou Maritime University，Guangzhou 510725，China

Abstract：By modeling the space of projective measured laminations in the cotangent space to Teichmüller space via hyperbolic length functions and extremal length functions，we associate two classes of linear structures to the space of measured laminations. We prove that both of these two linear structures are rigid：the induced linear structures on different Riemann surfaces are different.

Key words：Teichmüller space；measured laminations；linear structures；hyperbolic length；extremal length

Royden［1］proved the isometry rigidity of the Teichmüller metric in the sense that every isometry is induced by a mapping class of the underlying surface.Since then，the rigidity phenomenon in Teichmüller theory has been one of the main research interests in the field. So far，we know that the Teichmüller metric［1-3］，the Weil-Petersson metric［4-5］，the Thurston metric［6-8］，the mapping class group［9-10］，the curve complex and its relatives［11-12］，are all isometrically rigid. Ivanov proposed the following metaconjecture：

Ivanov Metaconjecture：Every object naturally associated to a surface and having a sufficiently rich structure has the extended mapping class group as its group of automorphisms. Moreover，this can be proved by a reduction to the theorem about the automorphisms of the curve complex.

In this paper，we consider a rigidity problem about the linear structures on the space of measured laminations，adding one more item to the rigidity list.

LetSbe an orientable surface of genusgwithnpunctures such that the Euler characteristic 2 - 2g-n＜0.LetXbe a hyperbolic metric onS. A geodesic lamination onXis a closed subset which can be foliated by simple

·transverse invariance：for any arck′obtained fromkby an isotopy respectingL，we haveμ(k) =μ(k′)；

·supported onL：for all arcs disjoint fromL，we haveμ(k) = 0.

A measured geodesic lamination is a geodesic lamination together with a transverse invariant measure. The simplest examples are the isotopy classes of simple closed geodesics onX. More precisely，for a simple closed curveαand a transverse arck，α(k) is defined to be the cardinality ofα∩k.LetCbe the set of isotopy classes of simple closed curves onS. Each measured geodesic laminationμdefines a functionμ：C→R，which associates toα∈Cthe geometric intersection numberi(μ，α) ?infμ(α)，where the infimum is taken over all representatives inα. LetML(X) be the space of measured geodesic laminations onXequipped with the weak topology from RC，the infinite product of R indexed byC. With respect to this topology，the set of weighted simple closed curves R＞0×Cis dense inML(X). The intersection pairingi：ML(X) ×C→R extends continuously to a homogeneous function onML(X) ×ML(X). By the one-to-one correspondence between simple closed geodesics ofXand simple closed geodesics of any other hyperbolic metric onS，the definition above does not depend on the choice ofX. For this reason，we shall denote byML(S) the space of measured geodesic laminations onSwithout referring to any specific choice of hyperbolic metric. LetPML(S)∶=ML(S)/R+be the space of projective equivalence classes of measured geodesic laminations.（For more details about measured geodesic laminations，we refer to［13-14］.）

It is known thatML(S) admits a piecewise linear structure［14］. This piecewise linear structure is very important in Teichmüller theory. In this note，we shall discuss some other linear structures onML(S)by modelling it into the tangent space（resp. cotangent space）of the Teichmüller spaceT(S) via hyperbolic length functions（resp.extremal length functions），see Proposition 1 and Proposition 4. Pan［8］proved an analogue of Royden's theorem in the setting of the Thurston metric. A key step in his proof is a related linearity rigidity of linear structures onML(S).

1 Modeled in the cotangent space via hyperbolic length functions

1.1 Teichmüller space of hyperbolic metrics

A marked hyperbolic surface is a pair (X，f) whereXis a hyperbolic surface andf：S→Xis an orientationpreserving homeomorphism. Two marked hyperbolic surfaces (X，f) and (X′，f′) are said to be equivalent if and only iff′°f-1：X→X′ is homotopic to an isometry. The Teichmüller spaceT(S) is defined to be the set of equivalence classes of marked hyperbolic surfaces. In the following，we shall simply denote the equivalence class[X，f]byX. It is well known thatT(S) is homeomorphic to R-3(2-2g-n).

1.2 Hyperbolic length functions

Recall thatCis the set of isotopy classes of simple closed curves onS. For eachα∈CandX∈T(S)，there is a unique geodesic representative ofαon the hyperbolic surfaceX.Letlα(X) be the length of this geodesic representative. This defines a function onT(S) ×C：

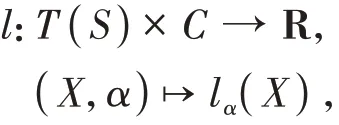
which admits a unique continuous extension：

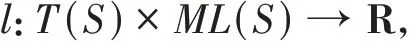
such thatltμ(X) =tlμ(X) for allt＞0，μ∈ML(S) andX∈T(S). For each measured geodesic laminationμ，lμ：T(S) →R is real analytic （for instance see［15，Corollary 2.2］）.

1.3 Linear structures via hyperbolic length functions

1.4 Earthquakes

1.5 Proof of Theorem 1

LetΠXY?DLY°DL-1X. IfY=X，thenΠXYis the identity map，which is linear. We now consider the converse.In the following，we assume thatΠXYis linear.

2 Modeled in the cotangent space via Extremal length functions

2.1 Teichmüller space of conformal structures

A marked conformal structure onSis a pair(X，f) whereXis a Riemann surface andf：S→Xis an orientation-preserving homeomorphism. Two marked conformal structures (X，f) and (X′，f′) are said to beequivalentif and only iff′ °f-1：X→X′is homotopic to a conformal map.The Teichmüller spaceT(S) can also be defined to be the set of equivalence classes of marked conformal structures. In the following，we shall simply denote the equivalence class[X，f]byX.

2.2 Extremal length functions

Letαbe an isotopy class of simple closed curve，andXbe a（marked）Riemann surface.A conformal metric onXis a metric which can be expressed asρ(z)|dz|locally.The extremal length ofαonXis defined by：

such thatExttμ(X) =t2Extμ(X)for allt＞0，μ∈ML(S) andX∈T(S). Moreover，for each measured laminationλ，the extremal length functionExtλ：T(S) →R is differentiable and positive.

2.3 Linear structures via extremal length functions

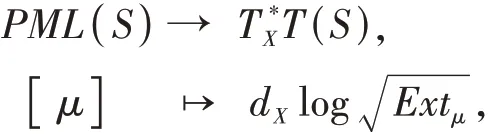
Proposition 4[19，Theorem4.1］For any complex structureX，the map embedsPML(S) as the boundary of a convex neighborhood of the origin.

By identifyingPML(S) with the subset{λ∈ML(S)：Extλ(X) = 1}，we obtain a homeomorphism：

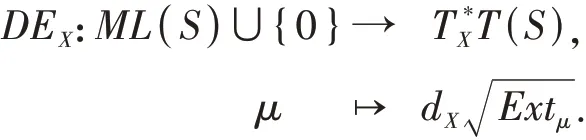
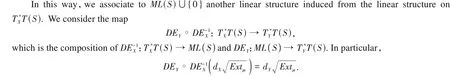
Theorem 2DEX°DE-1Yis linear if and only ifY=X.

ProofFor eachμ∈ML(S)，there exists a unique holomorphic quadratic differentialQ(μ，X) onXsuch that for every isotopy classαof simple closed curve，the geometric intersection number betweenαand the horizontal measured lamination ofQ(μ，X) is the same as the intersection number betweenαandμ. Letμ⊥Xbe the vertical measured lamination ofQ(μ，X).By Gardiner's formula［20，Theorem8］，（see also［21，Theorem 1.2］），we see that

Therefore，μ⊥X=μ⊥Y. Consequently，X=Y.

Remark 2Using the theory of lines of minima[22],we can prove Theorem 1 by the method above.More precisely, letXbe a hyperbolic surface andλa maximal lamination onX, i.e.λintersects every simple closed curve onX.Letμbe the unique measured lamination onXsuch thatdXlλ+dXlμ= 0.By Theorem 3.4 of[22],for such a pair (λ,μ), there exists a unique hyperbolic surfaceXin the Teichmüller spaceT(S) such thatdXlλ+dXlμ= 0.This implies thatDLY°DL-1X:T*XT(S) →T*YT(S) is linear if and only ifY=X,which is exactly Theorem 1.