參數不確定性下高效的可靠性靈敏度分析方法

陳志遠,李璐祎

西北工業大學 航空學院,西安 710072

靈敏度分析是研究和分析系統或模型的狀態或輸出響應對輸入參數和周圍條件的敏感性,它包括局部靈敏度分析和全局靈敏度分析。局部靈敏度分析通過保持參數在名義點處的值,每次改變一個輸入參數來檢查輸出的局部響應,因此它不能考慮輸入變量與其他輸入參數的交互影響對輸出響應的影響。全局靈敏度分析可以綜合考慮基本變量在其不確定性范圍內單獨變化以及與其他變量交互作用對輸出響應的平均影響,因此在工程設計和概率安全評估中取得了廣泛的運用。全局靈敏度分析起源于Cukier等于1973年提出的幾種不確定靈敏度指標,隨后得到了迅速發展,如Helton提出了非參數技術,但該方法缺少模型的獨立性；為了度量輸入變量的不確定性對模型輸出方差的影響,Sobol、Saltelli等提出了基于方差的全局靈敏度指標,之后出現了各種各樣方差靈敏度簡明高效的計算方法,例如：高維模型替代法(RS-HDMR)、狀態相關參數法(SDP)、隨機平衡設計過程(RBD)、基于蒙特卡洛的數值模擬法(MCS)等。為了分析基本變量對輸出整體分布的影響,Borgonovo等提出了基于概率密度函數的全局靈敏度指標。Li等之后將靈敏度指標引入到可靠性分析領域,提出了全局可靠性靈敏度指標。接著Wei等在Li等的基礎上進一步對可靠性靈敏度的定義進行了標準化,定義各輸入變量的主靈敏度和總靈敏度指標。Yun等將分數矩約束下的最大熵理論與Nataf轉換相結合提出了一種估計全局可靠性靈敏度指標的方法；蔣獻等通過Edgeworth級數展開將失效概率矩獨立全局靈敏度指標的求解轉化為輸出無條件及條件前四階整數矩的求解；Shi等提出了一種將稀疏網格技術與四矩法結合來估計全局可靠性靈敏度的方法。

上述方法都是在假設輸入變量的分布參數是已知的情況下進行的,即只考慮了輸入變量的不確定性。然而在工程實際中,正如Xu等所分析的,由于數據缺乏或條件限制,導致輸入變量分布參數不能準確確定,即分布參數也具有不確定性。分布參數不確定性被Ditlevsen、Haldar和Hajagos等稱為統計不確定性和二階不確定性。根據掌握的信息量多少,分布參數的不確定性通常可以采用區間、模糊隸屬函數、主觀概率密度函數等進行描述。確定性分布參數下模型輸出統計特征是確定的,如均值和方差；而分布參數不確定性會導致輸出統計特征也具有不確定性,因而輸入對輸出的影響也是不確定的,并由輸入變量的不確定性和分布參數的不確定性同時控制。因此,在靈敏度分析過程中,為了準確識別對輸出影響較大的輸入變量,就必須同時考慮輸入變量的分布參數在整個不確定范圍內對模型的影響。

目前,關于分布參數不確定性情況下基于方差的靈敏度分析已有一些研究。實現分布參數不確定性下的靈敏度分析的一個基本方法是三層嵌套Monte Carlo(MC)抽樣方法。該方法將分布參數在外層進行采樣,隨后在內層進行雙層循環抽樣以計算隨機輸入變量的靈敏度指標。但是這種方法計算成本過于高,不能直接用于實際工程問題。隨后,Saltelli等通過引入單層循環MC抽樣將三層嵌套MC抽樣簡化為雙層嵌套抽樣,在一定程度上減少了計算量,但是對于實際工程問題來說計算量還是過于龐大。Li等通過將代理抽樣密度函數與單層MC相結合,進一步將三層嵌套循環簡化為單層抽樣,能用較少的抽樣點得到精確的靈敏度估計結果。

以上都是參數不確定性下基于方差的全局靈敏度分析,這種靈敏度分析方法隱含地假設方差這一單一矩足以體現輸出的不確定性變化。但是,當分布被描述為某個具體的數值時,必然會造成信息的缺失。另外,在可靠性分析領域,工程實際更關心失效概率。大多數小失效概率與輸出的尾部分布有關,基本變量對輸出方差的影響并不等同于對失效概率的影響。Tang等利用失效概率(PFD)的互補累積分布函數定義PFD超過給定值的概率,分析了安全儀表系統(SIS)中具有截斷分布的認知不確定輸入參數對超出概率的影響。Chabridon等將參數不確定性下失效概率分布的平均估計(PFP)作為一種新的安全度量進行靈敏度分析,并提出了一種與自適應重要抽樣相結合的PFP估計策略；但該方法對于多失效域與高維問題所需的計算量非常龐大,計算效率較低。因此,為了準確評估參數不確定性下輸入變量對結構失效概率的影響,就需要發展新的基于可靠性的靈敏度指標及其求解高效的算法。

不同于基于方差的靈敏度分析,參數不確定性情況下基于可靠性的靈敏度分析一般需要在每個參數取值處重復進行可靠性分析,計算量難以為工程實際所接受。尤其是對于小失效概率結構系統,提高可靠性靈敏度分析效率一直是一大難點。因此,本文主要研究參數不確定性下輸入變量高效的可靠性靈敏度分析方法。所提方法首先將基于可靠性的全局靈敏度指標擴展到輸入變量及其分布參數同時具有不確定性的情況,定義了參數不確定性情況下輸入變量的主靈敏度指標以及總靈敏度指標。然后借鑒文獻[40]中的基于方差的靈敏度指標求解的單層抽樣方法,將參數不確定性情況下基于可靠性的靈敏度指標求解過程中的三層嵌套可靠性分析簡化為單層抽樣分析,極大地減少參數不確定性下可靠性靈敏度分析的計算量,并針對小失效概率問題,進一步將單層可靠性靈敏度分析與可靠性分析高效的重要抽樣(IS)以及截斷重要抽樣(TIS)結合起來。

本文所提方法的創新點分列如下：

1) 將基于方差的靈敏度分析的單層抽樣方法進一步擴展到可靠性分析領域。

2) 通過構造合適的重要代理抽樣概率密度函數(Surrogate Sampling Probability Density Function,SS-PDF),將單層可靠性靈敏度分析與高效的IS和TIS方法結合起來,解決參數不確定性情況下小失效概率結構系統基于可靠性的靈敏度分析計算代價大的問題。

1 參數不確定性下基于可靠性的全局靈敏度指標

1.1 基于可靠性的全局靈敏度指標

={:()≤}

(1)

相應的失效域指示函數定義為()：

(2)

結構系統的失效概率可表示為

(3)

式中:表示輸入變量的維空間。基于可靠性的全局靈敏度指標定義為

f|)()d

(4)

式中:f|=(|)為消除不確定性下的條件失效概率;代表一個隨機基本變量或者一組隨機基本變量(,…,), 1≤≤…≤≤。

文獻[22]進一步證明了：

(|)]}=[(|)]

(5)

式(5)表明：當將看作是模型輸出時,輸入變量基于可靠性的全局靈敏度指標就等同于失效域指示函數基于方差的全局靈敏度指標；因此,文獻[25]中定義了正則化的可靠性靈敏度指標：

(6)

其中單個輸入變量的主靈敏度指標為

(7)

總靈敏度指標為

(8)

式中:～為包含除了外的所有輸入變量。

1.2 參數不確定下全局靈敏度指標定義

當輸入變量=[,,…,]的分布參數受認知不確定性影響,計算模型將會同時包括分布參數的認知不確定性以及輸入變量的隨機不確定性。設=[,,…,]是輸入變量的維分布參數,其中是輸入變量相應的維分布參數,且++…+=。分布參數的認知不確定性可以有很多種表示形式,類似于文獻[30],本文采用概率密度函數()來描述輸入參數的認知不確定性。對于一個由()產生的認知參數,隨機輸入變量是通過條件概率密度函數(|)產生的。

當輸入變量的分布參數具有不確定性時,式(6)～式(8)中輸入變量對結構失效影響的可靠性靈敏度指標也不再是一個確定的值,而是一個隨著的分布參數的變化而變化的變量。為了準確衡量參數不確定性下輸入變量對失效概率的影響,就需要全面考慮輸入變量在整個參數空間內對失效概率的平均影響。因此,分布參數不確定性下輸入變量基于可靠性的主靈敏度和總靈敏度指標表示為

(9)

(10)

式中:((|))=()是無條件方差。

2 參數不確定性下基于可靠性的靈敏度指標的高效算法

式(9)、式(10)表明,參數不確定性下基于可靠性的靈敏度指標的直接求解需要三層循環嵌套的可靠性分析。即使對于分母中的無條件方差(),也需要雙層嵌套的可靠性分析過程,即在外層通過認知參數的邊緣密度函數對輸入變量的分布參數進行抽樣,內層在每一個參數的取值處進行可靠性分析得到條件方差(|)。這種嵌套的可靠性分析由于計算量很大并不適用于工程實際問題中。本節提出了參數不確定性下基于可靠性的靈敏度指標求解的3種高效算法。

2.1 代理抽樣蒙特卡洛法(S-MCS)

2.1.1 無條件方差的計算

其中無條件方差()可以轉化為

()=((|))=

(11)

(12)

式中:表示參數的維空間。

(13)

(14)

2.1.2 主靈敏度指標和總靈敏度指標的計算

將式(11)中的總方差公式應用于(～(|))后可以得到：

((～(|))|)=

(15)

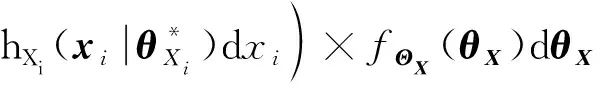
(16)

(17)

(～((|～))|)=

(18)

(19)

2.1.3 代理抽樣密度函數(SS-PDF)的選取

(20)

2.1.4 S-MCS抽樣步驟

(21)

(22)

2) 產生另一個×維樣本矩陣(),()中除第外的其他所有列是來自矩陣,第列中的元素是來自于矩陣:

(23)

3) 將矩陣、、()中的樣本代入輸出模型=()中,獲得相應的輸出值：

=(),=(),()=(())

(24)

再判斷輸出值是否落在失效域={:()≤}內,求出相應的指示函數：

F=(),F=(),F()=(())

(25)

4) 通過聯合概率密度函數()抽取的分布參數的個樣本：

(26)

(27)

(28)

(29)

則

(30)

可以看到盡管式(30)的求解是一個雙層嵌套抽樣形式,但是就功能函數的使用上而言,只是單層循環計算,總的計算量是(2+)。這和原始的三層循環嵌套抽樣的計算量(+)相比要小了很多。

2.2 代理重要抽樣法(S-IS)

2.2.1 代理重要抽樣密度函數

重要抽樣是通過重要抽樣概率密度函數()抽取樣本的,它的基本思想是：設計點是失效域中對失效概率貢獻最大的點,因此選擇密度中心在設計點的密度函數作為重要抽樣密度函數,可以使得抽取的樣本點有較大的概率落在對失效概率貢獻較大的區域,從而使得失效概率的估計值較快地收斂于真值。獨立標準正態空間中原概率密度函數()與重要抽樣密度函數()的等密度線的對比如圖1所示。

圖1 fX(x)與ψX(x)的等密度線對比圖[43]Fig.1 Isodensity line comparison diagram of fX(x) and ψX(x)[43]

由一次二階矩方法或者其他方法得到設計點。

2.2.2 代理重要抽樣法

(31)

同樣,可以得到：

(32)

(33)

(34)

(35)

產生另一個×維樣本矩陣(),()中除第外的其他所有列是來自矩陣,第列中的元素是來自于矩陣:

(36)

將矩陣、、()中的樣本代入輸出模型=()中,獲得相應的輸出值：

=(),=(),()=(())

(37)

再判斷輸出值是否落在失效域={:()≤}內,求出相應的指示函數：

F=(),F=(),F()=(())

(38)

通過聯合概率密度函數()抽取的分布參數的個樣本：

(39)

(40)

(41)

()通過如式(42)計算：

(42)

則

(43)

與代理蒙特卡洛抽樣(S-MCS)方法相比,代理重要抽樣(S-IS)方法通過將代理抽樣密度函數的抽樣中心移動到設計點,可以保證產生的大量樣本落入失效域內,因此更適合于解決參數不確定性下小失效概率結構系統的可靠性靈敏度分析問題。

2.3 代理截斷重要抽樣法(S-TIS)

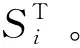
圖2 二維情況下β球示意圖[43]Fig.2 Schematic diagram of β-sphere in two-dimensional cases[43]

超球內安全樣本點功能函數的計算,從而達到在保證計算精度的同時提高可靠性分析效率的目的。

定義超球外區域內的指示函數()為

(44)

則式(31)中的無條件方差()轉化為

(45)

與式(17)推導過程相同,可以得到：

(46)

(47)

(48)

(49)

產生另一個×維樣本矩陣(),()中除第外的其他所有列是來自矩陣,第列中的元素是來自于矩陣：

(50)

由式(44)判斷、、()中的樣本點是否落在球外,求出相應的指示函數：

(51)

將矩陣、、()中篩選出的不為0的樣本分別記為′、′、′(),并代入輸出模型=()中,獲得相應的輸出值：

(52)

判斷輸出值′、′和′()是否落在失效域={:()≤}內,求出相應的指示函數：

(53)

對于矩陣、、()中為0的樣本無需代入模型中,直接在失效域指示函數,和中相應行插入0,由此得到完整的失效域指示函數矩陣F、F和F。

通過聯合概率密度函數()抽取的分布參數的個樣本：

(54)

(55)

(56)

()通過式(57)計算：

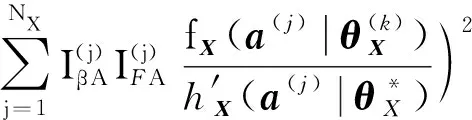
(57)

則

(58)

在上述步驟中,不需要計算那些落在球內的樣本點的函數值,因此S-TIS方法能在不損失精度的情況下進一步提高S-IS方法參數不確定性下全局可靠性靈敏度分析的效率。

3 算例分析

3.1 數值算例

考慮極限狀態函數：

由于算例1中的都服從于正態分布,所以選取的SS-PDF也服從于正態分布。根據SS-PDF的選取原則,算例1中所采用的SS-PDF服從的分布為～(4,45),(=1,2,3)。由AFOSM求解得到的設計點為(912,860,-108),因此S-IS和S-TIS方法采用的SS-PDF為～(912,45),～(860,45),～(-108,45)。

表1給出了用MCS、S-MCS、S-IS、S-TIS這4種方法計算的可靠性靈敏度指標,其中MCS方法為三層嵌套Monte Carlo抽樣法,其結果可以作為檢驗其他方法的參考解。為了方便對比,失效概率同樣也列入表中。為各個方法計算和所有變量可靠性靈敏度指標時所需的樣本量(確保和的變異系數cov都小于0.1),最后一項模型調用次數是計算過程中調用功能函數計算的總次數。表中估計值后面括號里的數字為其相應的變異系數cov,是通過對可靠性靈敏度指標和失效概率循環計算50次求出的結果。對于三層循環嵌套蒙特卡洛法,給定輸入變量數=3,分布參數的樣本量=1 000,輸入變量的樣本量,則模型調用次數為(+)；對于S-MCS方法,模型總的調用次數為(2+)；而對于S-IS,S-TIS方法,設計點迭代優化的次數=28,模型總的調用次數為(2+)+。

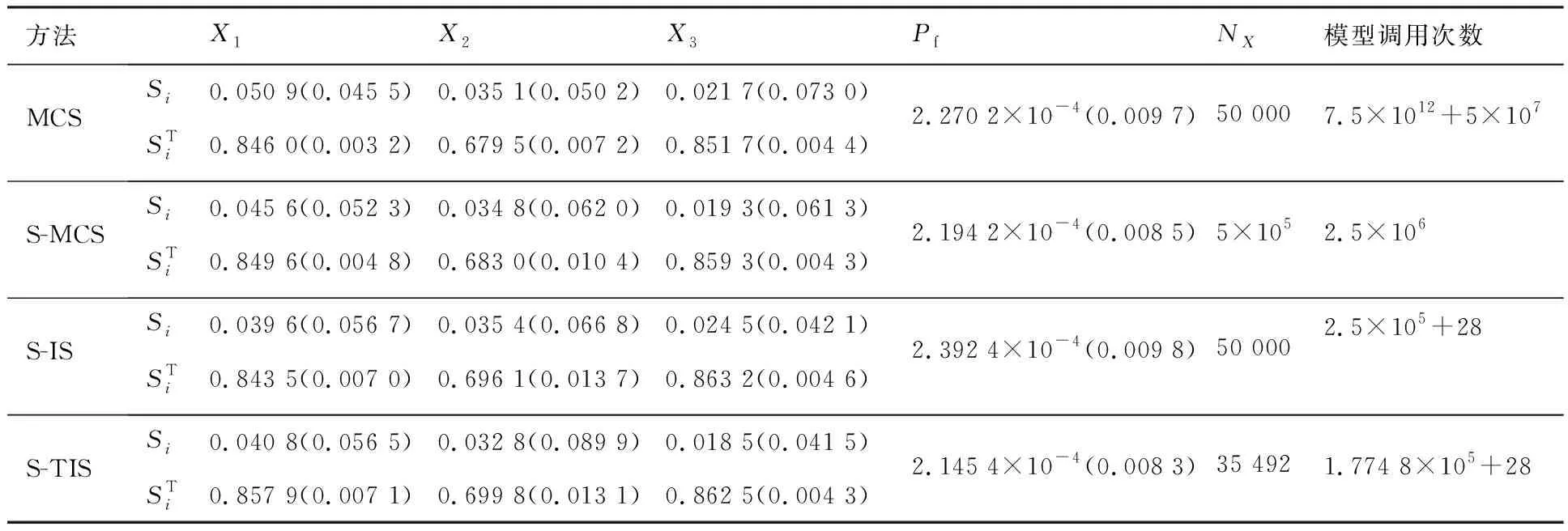
表1 4種方法的可靠性及可靠性靈敏度分析結果

從表1中可以看出,在失效概率比較小的情況下三層嵌套蒙特卡洛法(MCS)所調用的模型次數非常多,耗時很長；而代理抽樣蒙特卡洛法(S-MCS)通過把三層抽樣轉化為單層抽樣,大幅度減少了模型調用次數。代理重要抽樣法(S-IS)和代理截斷重要抽樣法(S-TIS)可以進一步以更加少的樣本量提供準確的可靠性靈敏度指標。

圖3 3種方法求解的S1和收斂曲線Fig.3 Convergence curves of S1 and for three methods

圖4 4種方法計算可靠性靈敏度指標對比圖(算例1)Fig.4 Comparison diagrams of reliability sensitivity indices for four methods (Case 1)

3.2 工程算例

在航空工程中,鈑金零件被廣泛使用,最常見的組裝方式是鉚接。鉚接過程中存在著許多影響鉚接質量的因素,其中擠壓應力是最主要的因素。擠壓應力過高可能導致鉚接失效。因此,控制鉚接過程中的擠壓應力對航空部件的安全具有重要意義。

真正的鉚接過程非常復雜,本文以無頭鉚釘為例,將鉚接過程簡化為圖5中的兩個階段。

在階段Ι,鉚釘從狀態A(鉚接前初始狀態,無變形)到狀態B(中間狀態,鉚釘和孔之間無間隙)。在階段Π,鉚釘由狀態B到狀態C(鉚接的最終狀態,鉚釘頭部變形)。整個鉚接過程中假設鉚釘體積不變。

為了建立擠壓應力和鉚釘尺寸間的關系,可以假設幾個理想條件：

1) 鉚接過程中鉚釘孔不擴大。

2) 鉚釘體積的變化可以忽略。

3) 鉚接結束后,鉚釘頭部為圓柱狀。

4) 材料為各項同性。

鉚接前,鉚釘的初始體積可以表示為

(59)

式中:和為狀態A時鉚釘的直徑和高度。

經過階段Ι,在狀態B時的鉚釘體積可以表示為

(60)

式中:和為狀態B時鉚釘的直徑和高度。

經過階段Π,假設鉚釘在狀態C的上、下部分尺寸相同,則鉚釘在狀態C的體積可表示為

(61)

式中:為薄壁件的整體厚度;和分別為狀態C時鉚釘頭的直徑和高度。

根據硬化強度理論,方向的最大擠壓應力可以表示為

=()

(62)

式中:為強度因子;為鉚釘材料的硬化因子;為鉚釘頭在鉚接過程中的真實應變。由兩部分組成：釘桿的鐓粗階段(階段Ι)的應變和鐓頭成形階段(階段Π)的應變,所以真實應變可以表示為

=+

(63)

假設鉚接過程中鉚釘的體積不變,整理式(63) 可得到鉚釘的最大擠壓應力為

(64)

文中選取鉚釘材料為2017—T4,其硬化指數=0.15,鐓頭高度=2.2 mm。根據材料手冊,鉚釘的擠壓強度為=580 MPa,如果最大擠壓應力大于擠壓強度,鉚釘就會出現失效,因此建立功能函數如下：

=-

(65)

圖5 簡化的鉚接過程Fig.5 Simplified riveting process

在整個鉚接過程中,鉚釘的尺寸和材料的特性可以認為是正態隨機變量,分布參數如表2所示。假設各輸入變量的均值也是正態變量,參數如表3所示。

表2 無頭鉚釘輸入變量的分布參數

表3 輸入變量均值的分布參數

為了使代理抽樣概率密度函數(SS-PDF)覆蓋整個輸入變量區間,在S-MCS中選定如下SS-PDF：～(5,06),～(20,08),～(51,05),～(5,07)。采用AFOSM求解得到的設計點為,因此S-IS和S-TIS方法中

采用的SS-PDF為～(446,07),～(55046,25)。

表4 4種方法的可靠性及可靠性靈敏度分析結果(算例2)

圖6 3種方法求解的Sd和的收斂曲線Fig.6 Convergence curves of Sd and for three methods

圖7 4種方法計算可靠性靈敏度指標對比圖(算例2)Fig.7 Comparison diagrams of reliability sensitivity indices for four methods (Case 2)

圖8 屋架結構示意圖Fig.8 A roof truss

表5 屋架結構輸入變量的分布參數

表6 輸入變量均值的分布參數

為了使代理抽樣概率密度函數覆蓋整個輸入變量區間,選定如下SS-PDF：～(20 000,1 100),～(12,032),～(982×10,(70×10)),～(004,0006),～(12×10,(462×10)),～(3×10, (3.52×10))。用AFOSM求解得到設計點

為(213 49,124,888×10,0032 4,1169×10,268×10),因此S-IS和S-TIS方法中采用的SS-PDF為～(21 349,1 100), ～(124,032),～(888×10,(70×10)),～(0032 4,0006)～(1169×10,(462×10))～(268×10,(352×10))。

表7 4種方法的可靠性及可靠性靈敏度分析結果(算例3)Table 7 Reliability and reliability sensitivity analysis results of four methods (Case 3)

4 結 論

1) 本文主要研究了參數不確定性下高效的可靠性靈敏度的分析方法。首先定義了參數不確定性下輸入變量基于可靠性的主靈敏度指標以及總靈敏度指標,以衡量輸入變量的不確定性在整個參數空間中對失效概率的平均影響。然后,借鑒已有單層抽樣的思想,通過引入代理抽樣概率密度函數將參數不確定性下可靠性靈敏度指標直接求解中的三層抽樣轉化為單層抽樣,大大減少了參數不確定情況下可靠性靈敏度指標分析的計算量。并針對小失效概率可靠性問題,進一步優化代理抽樣密度函數,并結合IS以及TIS思想,提出了更加高效的S-IS以及S-TIS方法。

2) 本文算例結果表明,和標準的三層循環嵌套抽樣蒙特卡洛法相比,S-MCS方法能不依賴于輸入變量及其參數的分布,以較少的計算量提供準確的可靠性靈敏度指標,S-IS以及S-TIS方法通過將代理抽樣密度函數的抽樣中心移動到設計點,保證產生的大量樣本落入失效域內,減少計算靈敏度指標所需抽取的樣本量,S-TIS方法更是通過去掉超球內的樣本點進一步減少了計算量。另外,各算例的結果表明,變量單獨作用對失效概率產生的影響可以忽略不計,這可能因為對于小失效概率結構系統,落入失效域內的樣本點較少,導致變量對失效概率的單獨作用影響也十分的小。

3) 在本文的S-IS以及S-TIS方法中,設計點是通過AFOSM數值計算得到的,對于高維問題來說其計算結果可能并不準確,這會在一定程度上影響方法的效率和精度。為了解決這一問題,可以采用模擬退火、馬爾科夫鏈、遺傳算法等方法進行設計點的優化選取,使得可靠性靈敏度的計算更加可靠。