古城墻本體內雨水入滲特征的影響研究

劉晨輝， 祝彥知， 李新明， 任克彬

(1.河南省文物建筑保護設計研究中心， 河南 鄭州 450002； 2.中原工學院 建筑工程學院， 河南 鄭州 450007；3.河南省文物建筑保護研究院， 河南 鄭州 450002)

降雨是誘發(fā)邊坡失穩(wěn)的重要因素，多數邊坡失穩(wěn)發(fā)生在降雨期間或降雨之后的一段時間內。土質城墻結構、形態(tài)與邊坡相似，同樣面臨降雨誘發(fā)失穩(wěn)的風險，城墻的破壞將會對人類文化遺產保護與傳承帶來嚴重威脅[1,2]。古城墻長期處于非飽和狀態(tài)，降雨期間，雨水沿城墻表面滲入本體，尤其是城墻表層土體松散，降雨入滲更加明顯。雨水入滲導致城墻本體含水率上升，基質吸力下降；根據土的非飽和剪切強度理論，基質吸力的降低將導致城墻潛在滑動面抗剪強度不斷降低，造成城墻失穩(wěn)破壞[3]。

非飽和土質城墻本體是一種復雜的三相土，雨水在城墻本體內部的運移是一個動態(tài)變化過程[4]。近年來，眾多學者研究水分在土體包氣帶中的運動規(guī)律，取得了豐富的成果。韓同春等[5]研究了降雨入滲率與降雨強度間的變化關系，揭示了入滲對雙層土邊坡的破壞機制；張社榮等[6]結合強度折減技術進行了瞬態(tài)滲流作用下的邊坡穩(wěn)定性計算；Anastasia等[7]探討了利用土體空間變異分析方法計算非飽和邊坡在降雨期間的穩(wěn)定性；石振明等[8]提出了多層非飽和土邊坡在降雨入滲過程中的穩(wěn)定性分析方法；趙金剛等[9]探討了填方邊坡在降雨蒸發(fā)循環(huán)作用下的變形特征，分析了其演化規(guī)律與誘發(fā)機制；吳長富等[10]根據實際氣象資料，利用非飽和土力學理論，研究了降雨作用下水分運移對邊坡穩(wěn)定性的時間及空間效應。已有研究中對降雨作用下邊坡及路堤內水分遷移和穩(wěn)定性的變化機制及工程應用進行了深入探索。其中對降雨強度、降雨歷時兩種降雨要素的研究成果最為豐碩，但對入滲表面對入滲速率及入滲量的重要影響研究不多。與邊坡、路堤相比，城墻有更大的入滲表面，包括頂面以及兩側坡面，如圖1所示。因此，考慮城墻特有較大入滲表面等結構特征的影響，分析城墻本體降雨入滲機制及穩(wěn)定性具有重要意義。

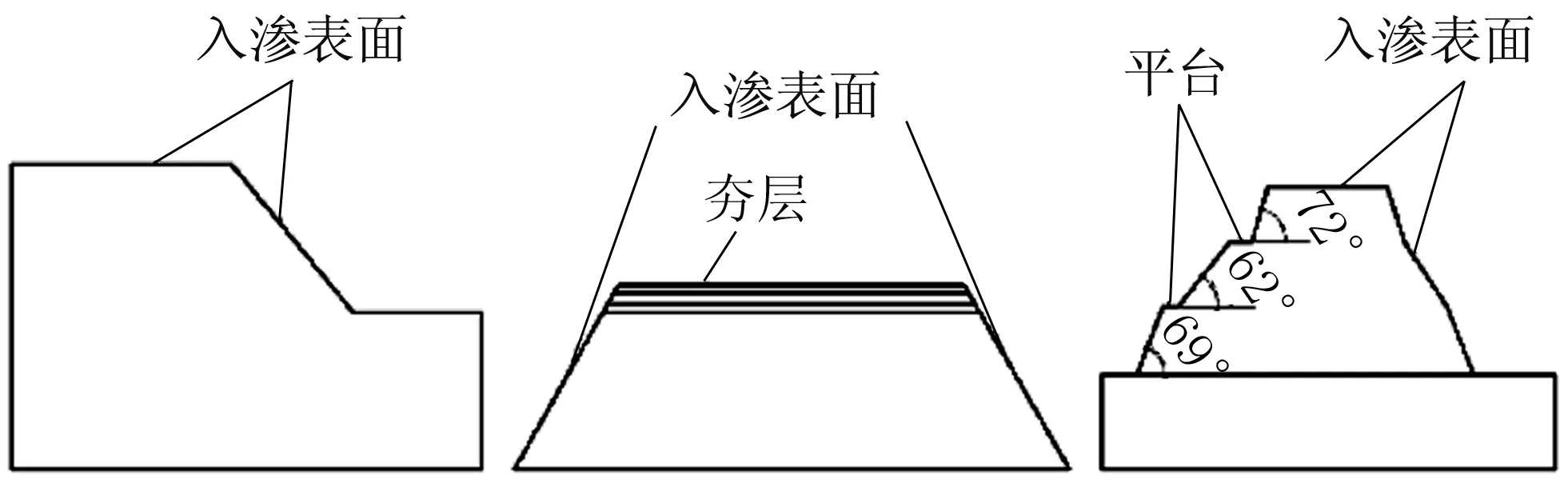
(a) 邊坡 (b) 路堤 (c) 城墻圖1 降雨入滲表面Fig. 1 Rainfall infiltration surface

本文以河南省新鄭市鄭韓故城城墻遺址為背景，利用有限元軟件ABAQUS，分析了不同降雨要素下，古城墻遺址特有的較大入滲表面結構特征對城墻本體孔隙水壓力、速度矢量場以及飽和度變化的影響；并探討了城墻坡面、平臺對城墻本體內水分入滲作用的影響，研究成果可為揭示降雨誘發(fā)城墻失穩(wěn)機制提供依據。

1 水分運移基本方程

降雨作用下的城墻本體滲流場分析中，降雨入滲形成的水分運移可概括為城墻剖面上的瞬態(tài)非飽和滲流場，此過程遵循達西定律和質量守恒定律。

1.1 非飽和土達西定律

1931年，Richards將達西定律推廣解決非飽和液體流動問題，其中考慮了滲透系數與吸力或吸力水頭之間的影響。非飽和土中水分運動的方程可表示為[11]：

(1)

式中：θ為體積含水率；hm為基質吸力水頭；kx(hm)、kz(hm)分別為x、z方向上以土體體積含水率和基質勢為自變量的非飽和滲透系數函數。

1.2 質量守恒原理

質量守恒原理是指對于一個給定的土體單元，水的損失或補給率是守恒的，等于水流入與流出土體單元的凈流量。質量守恒原理也稱連續(xù)性原理。由此可得：

(2)

式中：Vwx為水平水分通量；Vp為豎直水分通量。此式是土中水分非穩(wěn)定滲流或瞬態(tài)滲流的控制方程，既適用于飽和土也適用于非飽和土。

1.3 瞬態(tài)非飽和滲流

根據質量守恒原理，將式(1)代入式(2)，可得二維單元體內降雨入滲的非飽和土質城墻入滲的偏微分方程：

(3)

式中：z坐標方向附加的一項是由位置水頭引起的。

1.4 土水特征曲線與滲透系數曲線的描述

在飽和非飽和滲流數值計算中，城墻本體的滲透系數與其斷面的飽和度、孔隙水壓力的分布及大小相關。土體體積含水率和孔隙水壓力的關系即為土水特征曲線，這是描述非飽和土強度與滲透系數的重要工具；將滲透系數與孔隙水壓力聯(lián)系起來即為滲透系數曲線[12-14]。模型中土水分特征曲線與水力參數的函數關系為：

(4)

(5)

式中：θ是體積含水率；θr是殘余含水率；θs是飽和含水率；Ks是飽和滲透系數；a、m、n是土水特征曲線形狀參數；φ是基質吸力。

2 計算模型、參數及方案

2.1 計算模型

模型范圍的大小對有限元計算，尤其是滲流場計算有較大的影響。根據鄭穎人等關于邊坡模型的研究[15]，結合城墻模型，將墻腳至模型邊界的距離取為城墻高度的2倍，且模型上下邊界的高度不低于2倍的城墻高度。

圖2 有限元計算模型Fig. 2 Finite element calculation model

圖2所示為鄭韓故城北城墻段的一個典型剖面計算模型，計算網格單元數量為1 904，節(jié)點數量為2 015。從計算模型中可知，城墻本體的降雨入滲表面為整個城墻外表面輪廓，與邊坡、路堤相比，較大入滲表面意味著更多的入滲量，這對整個城墻剖面內雨水運移產生較大影響。此外，外界環(huán)境造成城墻表面特有的多平臺，坡面也會加劇本體內各個位置間較大的滲流差異。

由于模型區(qū)域較大，選取特征點以及特征路徑量化城墻本體孔隙水壓力及滲流速率等的變化規(guī)律。其中，特征路徑Ⅰ是從城墻最高處沿豎直方向到模型底部；特征點A、B、C、D的高度依次為14 m、9.05 m、5.77 m、3.96 m；特征點E、F、G則依次位于模型左側不同坡角(71.7°、25.7°、0°)的城墻表層土體部位。

2.2 計算參數、初始條件

(1) 計算參數。根據《土工試驗方法標準》(GB/T 50123-2019)，通過變水頭滲透試驗法，計算得到該城墻段的飽和滲透系數平均為5×10-6m/s。由于城墻本體內各位置的滲透系數由基質吸力與初始含水率共同決定，根據非飽和土力學理論，通過Van-Genuchten模型進行擬合，求得城墻土的土水特征曲線(SWCC)，見圖3；土體滲透系數同樣利用Van-Genuchten滲透系數模型擬合試驗所得如圖4所示。

圖3 土水特征曲線圖Fig. 3 Soil-water characteristic curve

圖4 滲透性函數曲線圖Fig. 4 Permeability function curve

(2) 初始條件。地下水位于地表以下10 m處，城墻上表面初始孔隙水壓力為-264.7 kPa。圖5所示為城墻剖面路徑Ⅰ上初始孔隙水壓力隨高度的變化規(guī)律。

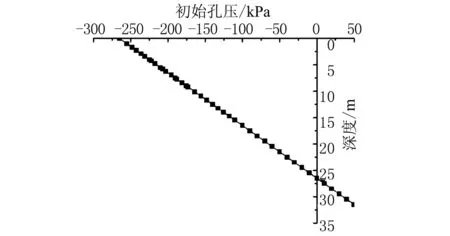
圖5 初始孔隙水壓力分布圖Fig. 5 Initial pore water pressure distribution

(3) 邊界條件。將降雨強度轉化為表面流量邊界施加于模型表面。當降雨強度不大于土體的滲透系數時，按照降雨強度設置流量邊界；當降雨強度大于土體滲透系數時，將在城墻表面形成徑流和積水，此時的流量邊界按照飽和滲透系數設置[3]。

2.3 計算方案

受城墻較大入滲表面影響，研究城墻內部水分運移規(guī)律對不同降雨要素的響應是十分必要的[16]。依據降雨強度，降雨歷時，設置如表1所示3種降雨方案對城墻降雨入滲過程進行數值模擬。

表1 降雨強度分布和參數設計

3 計算結果與分析

3.1 城墻孔隙水壓力

降雨作用下，城墻穩(wěn)定性受多重因素影響，其中基質吸力降低甚至形成正孔隙水壓力，會造成土體有效應力降低，威脅城墻本體安全。鑒于此，將降雨強度按照節(jié)點流量施加于模型表面，分析城墻本體內不同位置特征點在上述3種降雨方案下的變化情況，揭示城墻孔隙水壓力在降雨作用下的變化規(guī)律，結果如圖6所示。

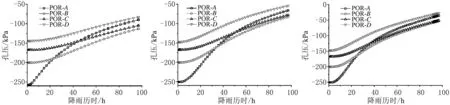
(a) 方案一(降雨強度0.05Ks) (b) 方案二(降雨強度0.1Ks) (c) 方案三(降雨強度0.2Ks)圖6 特征點A-D孔隙水壓力隨降雨歷時的變化Fig. 6 Variation of pore water pressure at characteristic points A-D with rainfall duration

特征點A、B、C、D分別位于城墻剖面從上到下不同高度處，各特征點位置受地下水、自然環(huán)境等因素影響差異較大。從圖6可以看出，初始孔隙水壓力(絕對值)隨高度的增加逐漸增大，含水率逐漸減小。降雨歷時96 h后，D點基質吸力最小。分析可知，初始基質吸力越小，滲透系數越大，同時受入滲面積較大影響，雨水在初始基質吸力較小的位置快速入滲，孔隙水壓力顯著增大。此外，在任一降雨條件下，城墻表面基質吸力(絕對值)隨降雨歷時的增加而降低，直至0 kPa，即飽和狀態(tài)。具體表現為：同一降雨強度下，初始基質吸力較大的城墻表面，其孔隙水壓力上升速率快于初始基質吸力較低的城墻表面。

同一基質吸力條件下，相同降雨歷時的城墻表面孔隙水壓力上升幅值隨降雨強度增大而增大，單位時間入滲量以及本體的滲流速率也都有明顯提高，極大促使基質吸力(絕對值)快速減小。

3.2 速度矢量場

速度矢量場的變化反映了雨水滲入城墻本體時，滲流速度受降雨強度、初始含水率和滲透系數等多重影響因素的變化情況。3種降雨強度下，路徑Ⅰ上各節(jié)點的滲流速率隨降雨入滲深度的變化規(guī)律如圖7所示。

(a) 方案一(降雨強度0.05Ks) (b) 方案二(降雨強度0.1Ks) (c) 方案三(降雨強度0.2Ks)圖7 不同高度處的滲流速率Fig. 7 Seepage rate with depth

從圖7看出，在一定入滲深度范圍內，路徑Ⅰ上各節(jié)點的滲流速率變化較大；大于這一影響深度后，滲流速率降為0。

此外，任一降雨條件下，距地表一定深度范圍內的滲流速率隨降雨歷時的增加而增大。分析原因可知，在任一降雨強度下，雨水不斷入滲補充城墻本體，且表面入滲流速大于濕潤鋒的出滲速度，致使雨水在濕潤鋒上方未滲出而逐漸累積，導致表層土體接近飽和狀態(tài)，造成路徑Ⅰ上一定深度范圍內的含水率增大，滲流速率變大。此外，對比不同方案下表層滲流速率可知，隨著降雨強度的增大，城墻表層滲流速率有顯著提高。這表明降雨強度在一定程度上也會決定城墻表層土體的入滲速率以及入滲量。

3.3 入滲深度

明確城墻本體受降雨入滲影響的深度范圍，是計算城墻滑動面以上下滑力增大值的前提[17]。從前述結果可以看出，在任一降雨強度下，城墻本體一定深度范圍內的滲流速率有較大變化，大于這一深度值后，滲流速率將變?yōu)?，此深度值即為降雨入滲的影響深度。三種降雨方案對應的入滲深度影響規(guī)律類似。將方案二所對應的降雨強度施加于城墻表面，分析飽和度在路徑Ⅰ上隨深度的變化情況，由此可直觀看到不同降雨歷時下的降雨入滲影響深度，如圖8所示。

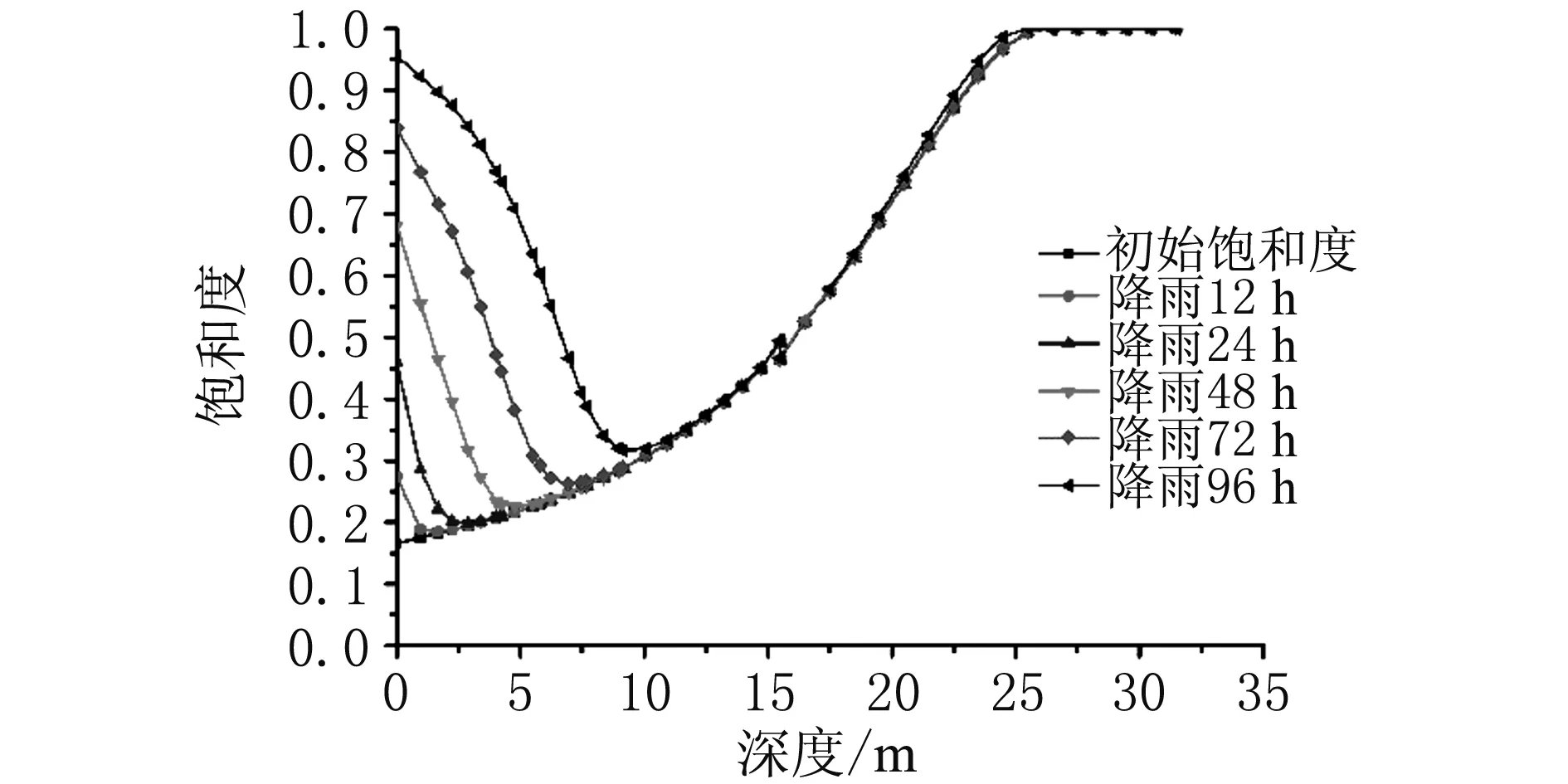
圖8 飽和度隨深度的變化Fig. 8 Variation of saturation with depth

由圖8可知，任一時刻下，飽和度在城墻深度范圍內的變化規(guī)律是相似的。受降雨入滲作用影響，表層土體的飽和度有所提高，且飽和度的增長幅度與降雨歷時呈正相關關系；在表層土以下，隨著深度的增加，飽和度逐漸變小。任一降雨歷時下，大于影響深度的本體部分，其飽和度隨深度變化的曲線與初始飽和度曲線相重合，此重合處對應的深度值即為降雨入滲的影響深度。降雨歷時越長，入滲影響深度越大，超過影響深度范圍的土體飽和度則不受降雨入滲影響。

降雨入滲影響深度范圍內，滲流引起土體含水率增大、基質吸力減小、土體重度增大以及滑動面以上下滑力變大，這對土體強度及城墻穩(wěn)定性而言是非常不利的。基于方案二的降雨強度作用下，降雨歷時與降雨入滲影響深度的關系如表2所示。

表2 不同降雨歷時下的入滲影響深度

3.4 坡角和平臺

從圖2可以看出，城墻左側從上到下呈現不同的梯級，而階梯狀的結構(不同坡角的坡面、平臺)會影響降雨入滲過程，進而影響城墻表面孔隙水壓力、飽和度的變化。現選取城墻左側特征點E、F、G，分析不同坡角對城墻本體內滲流規(guī)律的影響。表3所示為特征點E、F、G所在城墻表層土體地表與地面的夾角(以逆時針方向為正)。特征點E、F、G在降雨強度為0.2Ksm/s時，各特征點飽和度隨降雨歷時的變化規(guī)律如圖9所示。

表3 特征點位置

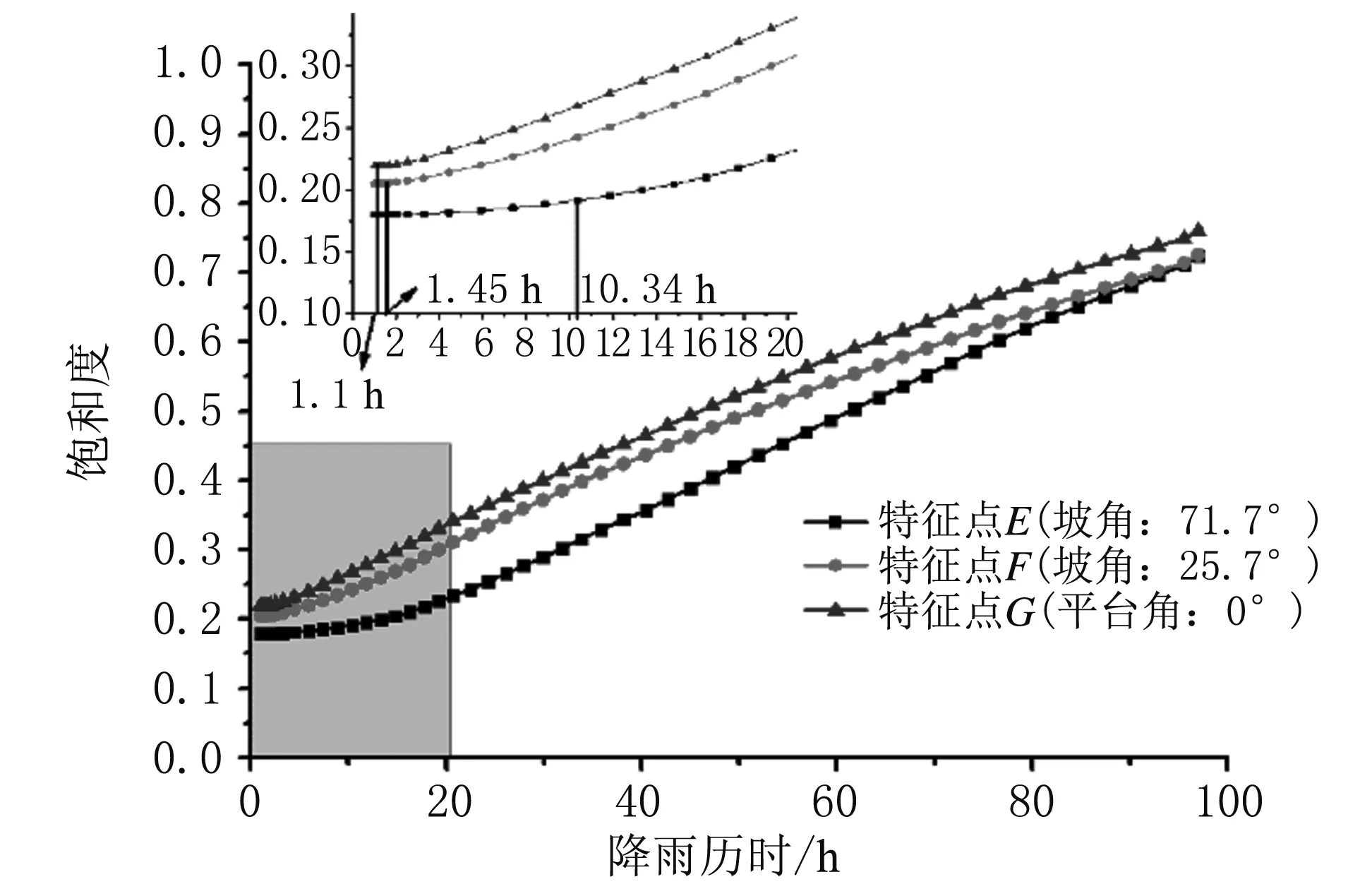
圖9 飽和度隨時間的變化過程Fig. 9 Variation of saturation with time

由圖9可知，降雨期間，各特征點處飽和度隨降雨歷時的增加不斷增大；特征點G(坡角0°，平臺處)的飽和度始終大于特征點E、F，其中特征點E(坡角71.7°)處飽和度最小。值得注意的是，城墻左側平臺以下0.5 m 深度處的特征點G是在降雨1.1 h后飽和度開始發(fā)生變化，且增長速率較大；特征點F(坡角25.7°坡面)的飽和度是在1.48 h之后有明顯增長；而特征點E在降雨10.34 h之后飽和度才出現明顯的增幅，且增長速率明顯小于特征點F、G。這是由于降雨期間特征點G所在的城墻平臺處將匯集更多上部雨水徑流，使得入滲率更大，受降雨影響的響應時間也最短；而在特征點E、F之間，隨著坡角的增大，入滲率以及單位時間入滲量減小，受降雨影響的響應時間也增加。因此，飽和度以及飽和度的變化速率在城墻左側平臺處最大，隨著坡角的增大而減小。此外，隨著降雨歷時的增加，飽和度增大，但增長速率有所減緩，且趨于相同。可見，城墻的結構特征(坡角、平臺)是影響城墻降雨入滲的重要因素，尤其是降雨對城墻平臺處的影響最大，平臺處失穩(wěn)風險更大，所以在古城墻遺址的修繕保護中，應對城墻平臺處的防排水予以足夠的重視。

4 結論

(1) 城墻較大的入滲表面使得本體內的水分運移復雜多變。在同一降雨強度作用下，城墻外表面孔隙水壓力上升速率隨初始基質吸力大而增大，孔隙水壓力的動態(tài)變化過程(變化速率、變化幅值)與降雨強度呈正相關。

(2) 降雨歷時越長，雨水入滲影響深度越大。雨水在城墻本體內的運移速率由城墻表層向深部逐漸減小，但減小幅度與影響深度有關。入滲影響深度范圍內，飽和度均有所提高；濕潤鋒以下，飽和度將不受影響。

(3) 同一降雨條件下，城墻平臺處飽和度始終大于坡面處表層土體。降雨初期，平臺處飽和度增長速率顯著大于坡面；降雨后期，城墻平臺和坡面飽和度增速均減緩，差異性也隨之變小。

(4) 依據非飽和土強度理論，平臺處飽和度增幅越大，土體抗剪強度越小，失穩(wěn)風險越大，因此在日常維護工作中，應重視城墻表面平臺處的風險監(jiān)測及防排水工作。