林業產業資產證券化風險測度研究
——基于AHP層次分析法和模糊綜合評價法

朱子超，劉金龍

(招商銀行股份有限公司，廣東 深圳 518040)

1 引言

在我國經濟社會發展和銀行金融創新的雙輪驅動下，林業產業資產證券化(ABS)迎來了機會之窗。林業產業是一個涵蓋了國民經濟第一、第二、第三產業的綜合型產業。近20年來其總產值高速發展，帶來了十分可觀的經濟效益、社會效益和生態效益。但長期以來，市場化的林業金融支持非常滯后，在一定程度上制約了林業產業發展。隨著林業產業結構不斷優化、林業金融政策支持力度不斷增大、資本市場日趨成熟、商業銀行金融創新日益迅速，資產證券化成為解決林業融資困境、間接引入社會資本的重要手段。林業產業資產證券化，是指以林業產業基礎資產未來可產生的穩定的現金流為償付條件，在公開市場上發行證券的過程。商業銀行借助表內資金或者理財資金，在公開市場認購“林業產業資產支持證券”，以達到為林業企業融資的目的。如此一來，既盤活了林業企業沉重的資產，又開拓了商業銀行的金融實踐之路。由于資產證券化屬于銀行的表外業務，不受巴塞爾協議中對于核心資本充足率、資本充足率的嚴格限制，因此商業銀行存在借助資產證券化進行監管套利的可能(楊繼光，2009)，表面上看沒有資本成本的消耗，實際上卻加劇了整體商業銀行的風險累積。

2 文獻回顧與評述

2.1 林業產業資產證券化風險研究

林業經濟學者潘煥學(2006)在研究中首次提出森林資源ABS這一理念，從信貸供給和信貸需求兩個角度，分別分析了林業資產證券化的必要性和可行性。那洪生(2009)通過研究國外和國內的林業產業發展特點，認為我國林業ABS缺少完善的制度條文和必要的風險管理措施。張瑜(2009)從資本市場的角度分析了林業上市公司與資本市場的相互作用，認為資本市場的成熟對林業產業ABS的發展有促進作用。盧偉(2010)通過永安林業的例子具體分析了證券化一般原理和可行性，得出林業產業資產證券化具有風險易可控和融資成本較低的結論。盛均全(2012)通過理論與實踐相結合的方法，提出了我國林業產業資產證券化融資模式的一般模型和風險因子。劉士磊(2013)從模式選擇的角度分析了森林資源資產證券化的可行性，并通過結合AHP層次分析法和SWOT模型全面研究出了林業產業資產證券化的SWOT因子及各維度影響程度，得到了各個風險的權重。杜鵬(2015)通過案例分析的方法，以廣州某森林旅游景區為例，分析了未來門票收益權證券化的運作模式，提出資產產權問題是很大風險所在，會導致資產證券化業務無法進行。劉龍龍(2017)通過案例分析的方法，研究了云南某森林景區未來收益資產證券化的融資模式和風險防范。建議建立政府主導型市場、加強信息披露、完善法律體系和降低投資者準入標準等。

2.2 文獻回顧綜述

在文獻回顧中，已有諸多學者從林業經營和資產證券化角度分析了其中的風險因子。但已有文獻卻忽視了在投商行一體化下，當商業銀行作為投資者進入資本市場時，如何建立授信風險評價標準、如何更加有效地進行林業產業供給側創新這一亟待解決的課題。

3 理論依據和研究方法

3.1 理論依據和指標體系構建

本研究首先通過專家調查問卷的方式，得到本研究的研究對象——AHP層次分析模型，如圖1所示。

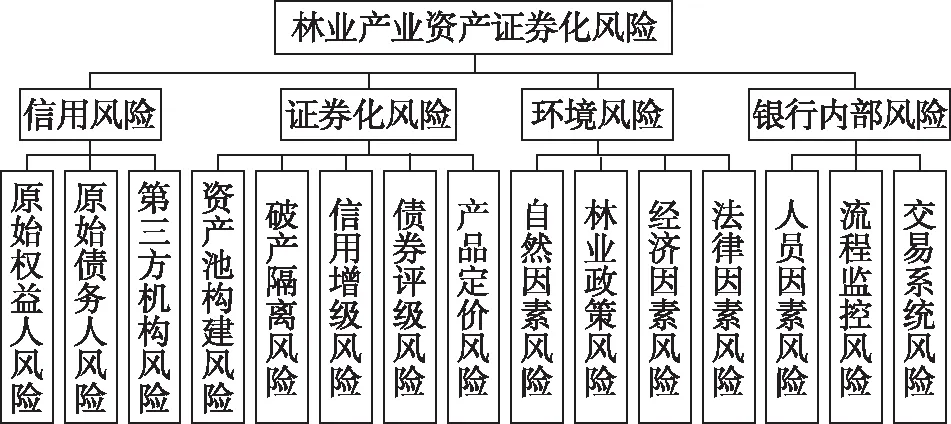
圖1 林業產業資產證券化風險測度AHP層次分析模型

3.2 研究方法

3.2.1 AHP層次分析法綜述

本研究采用模糊層次分析法對資產證券化風險進行定量分析，模糊層次分析法是層次分析法(AHP)和模糊綜合評價法的結合運用，前者用于分析各個風險因素的權重，后者用于分析各個林業產業的風險評語隸屬等級和整體風險得分。

3.2.2 AHP層次分析法數學公式說明和數學分析步驟

(1)求判別矩陣A(Judgement Matrix)。設受某準則(例：風險)支配的元素,, …,相對于的重要性測度(排序測度)分別為,, …,， 則個元素之間通過相應測度的兩兩比較，形成相對測度比，其矩陣形式為：

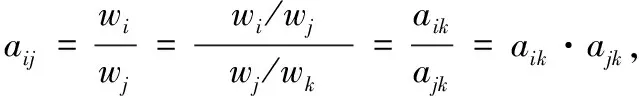
(2)計算重要性排序。根據Perror-Frobineus理論可以得到比正反矩陣更廣泛的非負不可約矩陣存在唯一模為最大的特征根，其對應的特征向量全部由正分量組成。即由=，其最大特征根所對應的特征向量=(,, …,)。

為判斷矩陣的最大特征根，歸一化處理后的向量就是排序用的權重向量。這種求得權重向量的方法稱為特征根法(Eigenvalue Method)。

(3)求最大特征根。

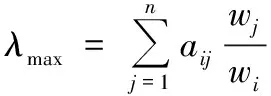
(4)求判別矩陣的一般一致性指標值。

=(-)(-1),為對應矩陣的維度

(5)求判別矩陣的隨機一致性比率。=，其中為判斷矩陣的平均隨機一致性指標，的值可由表1得出。

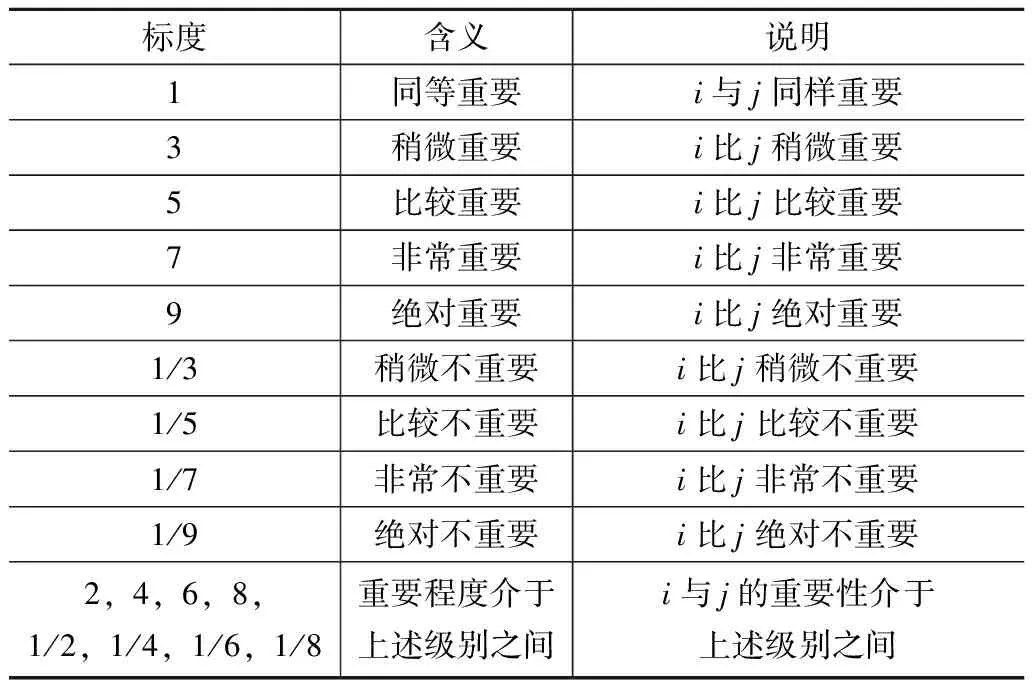
表1 判別矩陣標度與含義

(6)APH一致性判別標準。若值小于0.1，則說明有較好的一致性。在一致性檢驗中包含了層次單排序檢驗和層次總排序檢驗。

(7)群決策選擇。在此次研究中，各專家群決策各權重結論值，直接等于所有專家的各相應權重值的平均值。如果各專家影響因子不同，則平均值為各專家的加權平均值。

3.2.3 模糊綜合評價核心觀念“隸屬度”定義和數學分析步驟

模糊綜合評價法是一種基于模糊數學的評價方法。模糊數學在模糊理論的基礎上發展而來，將所討論的對象限制在一定的范圍內，那么所討論對象的全體為論域，用表示。在論域中，對于任意一個屬于論域的元素x，若x以某個程度(∈[0, 1])屬于集合,而不是∈或者x不屬于，那么集合稱為模糊集合。在經典數學中，一般采用特征函數表示元素和集合的關系，而特征函數的取值只有1(元素x在論域中)和0(元素x不在論域中)兩種情況。在模糊集合中，特征函數的取值在區間[0, 1]上，教授用隸屬度函數來表述。隸屬度是指，設論域，如果存在():→[0, 1]，則稱()為∈的隸屬度，則()為的隸屬度函數。該評價法根據模糊數學的隸屬度理論，即通過數學的方法將一些主觀的、難以界定的模糊評價進行定量劃分，得到量化測度結果。

4 定量分析過程

4.1 AHP層次分析法——構造判別矩陣

借助AHP軟件，構造林業產業資產證券化風險測度判斷矩陣、信用風險測度判斷矩陣、證券化風險測度判斷矩陣、環境風險測度判斷矩陣、銀行內部風險測度判斷矩陣五個風險測度判斷矩陣。

4.2 層次單排序和一致性檢驗

AHP層次分析法要檢驗判別矩陣的一致性，即評價中前后邏輯是否一致。其中，依據前述一致性檢驗標準，值可由表2得出。

表2

資料來源：根據竇玉丹(2011)研究整理制作。

根據薩蒂教授的研究，當判斷矩陣的<01或=即CI=0時,則認為該判別矩陣具有滿意的一致性。

4.2.1矩陣層次單排序與一致性檢驗

=(03436 04985 00538 01041)；(·)=(1405 20313 02216 04299)；=∑()n=41031，=09，n=4；=(λ-n)/(n-1)=(41031-4)(4-1)=00344；==0034409=00382；因為<01,所以矩陣通過了一致性檢驗。

4.2.2矩陣層次單排序與一致性檢驗

=(0672 02329 00951)；(·)=(20309 07038 02872)；=∑()=3022，=058，=3；=(-)(-1)=(3022-3)(3-1)=0011；==0011058=00189；因為<01,所以矩陣通過了一致性檢驗。

4.2.3矩陣層次單排序與一致性檢驗

矩陣歸1化最大特征向量(權重向量)： =(04759 01205 01145 02534 00357)；(·)=(24914 0617 05825 13131 0189)；λ=∑()n=51834，=112，n=5；=(λ-n)/(n-1)=(51834-5)(5-1)=00458；==00458112=00409；因為<01,所以矩陣通過了一致性檢驗。

4.2.4矩陣層次單排序與一致性檢驗

=(05897 01636 01994 00474)；(·) =(24771 067 0815 02004)；=∑()n=41539，=09，n=4；=(λ-n)/(n-1)=(41539-4)(4-1)=00513；==0051309=0057；因為<01,所以矩陣通過了一致性檢驗。

4.2.5矩陣層次單排序與一致性檢驗

=(05934 0335 00716)；(·)=(17864 10086 02155)；=∑()=30106，=058，=3；=(-)(-1)=(30106-3)(3-1)=00053；==00053058=00091；因為<01,所以矩陣通過了一致性檢驗。

上述的計算結論表明，在層次待排序中，各個矩陣均通過了一致性檢驗。

4.3 層次總排序一致性檢驗

進行完層次單排序一致性檢驗后，要進行層次總排序的一致性檢驗。層次總排序依然要通過計算值進行判斷。=(0343638×0011+0498481×00458+00538074×00513+0104073×00053)(0343638×058+0498481×112+00538074×09+0104073×058)=00346。因為層次總排序的<01，通過了一致性檢驗。因此本次研究中的風險評價模型比較合理，可以用于進一步研究。

4.4 模糊綜合評價定量分析

4.4.1 導入評測指標權重集

導入底層指標所對應的結論值權重并建立評測結論集。

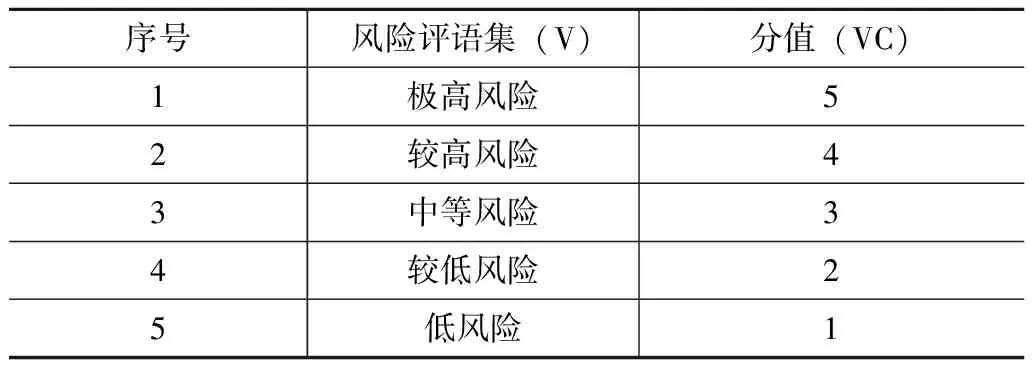
表3 風險評測結論集

根據M銀行2021年信貸政策，把信貸風險程度劃分為1～5的風險等級標度，若風險得分越接近于5分，則說明風險越高；越趨近于1分，則說明風險越低。

4.4.2 模糊算子選擇

根據葛允康和孫英雋(2014)對模糊算子的研究，常見的模糊算子有：(∧，∨)、(?，∨)、(∧，+)、(?，+)。本研究選擇(?，+)算子，即1相乘，2相加。之所以選擇此加權平均型算子，是因為這種算子在計算中綜合性、信息整合性更強。

4.4.3 模糊綜合評價分析

借助于AHP軟件，利用前述選定的合成算子進行合成，得到各個風險評價因素的模糊綜合評價結論向量。且按照最大隸屬度原則，運用加權平均求隸屬等級的方法，對評價結果進行綜合計算得出最后的風險分數，再根據數據計算結果劃分風險域。其中，為模糊綜合評判集；為前述重要性權重集；為“備擇集”，即專家對評判對象可能作出的各種總的評判結果(元素)組成的集合：極高風險、較高風險、中等風險、較低風險、低風險；為備擇集分值1～5分；為模糊綜合得分，其公式為=·。具體步驟為：

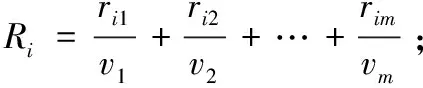
依據上述步驟，分別針對林業第一、第二、第三產業進行模糊綜合評價。

444 林業第一產業資產證券化模糊綜合評價

=·=(0173491；0412494；0345868；00547747；00133726)。

=·=0173491×5+0412494×4+0345868×3+00547747×2+00133726×1=367796

通過模糊綜合評價定量分析，林業第一產業資產證券化風險得分367796分。

445 林業第二產業資產證券化模糊綜合評價

=·=(000107231；0362523；0430318；0163619；00424676)

=·=000107231×5+0362523×4+0430318×3+0163619×2+00424676×1=311611

通過AHP和模糊綜合評價定量分析，林業第二產業資產證券化風險得分3.11611分。

4.4.6 林業第三產業資產證券化模糊綜合評價

B=W·R=(0.0126868；0.129019；0.434105；0.352681；0.0715086)

=·=00126868×5+0129019×4+0434105×3+0352681×2+00715086×1=265869

通過模糊綜合評價定量分析，林業第三產業資產證券化風險評價得分2.65869分。

5 結果和討論

5.1 AHP層次分析數據討論

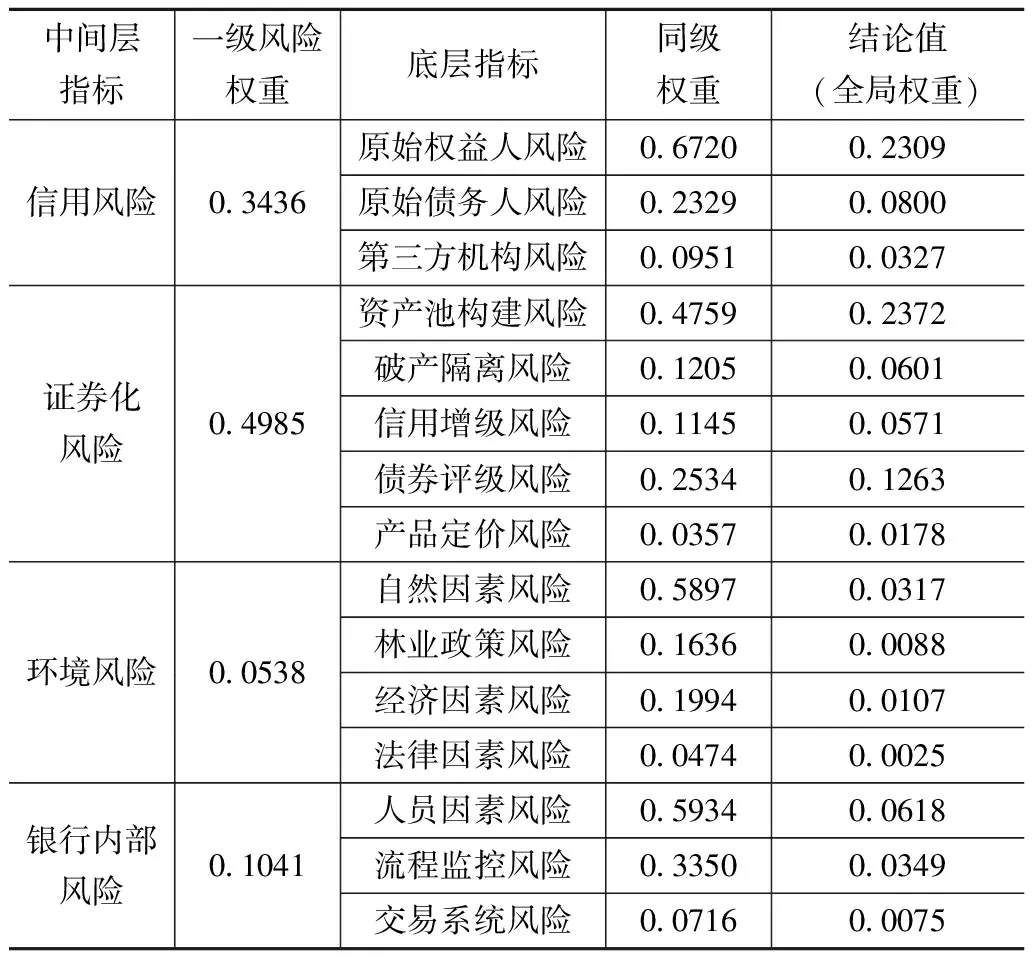
表4 林業產業資產證券化風險評價權重分配

權重最大的前三位為資產池構建風險(23.72%)，原始權益人風險(23.09)，債券評級風險(12.63%)，這三項已貢獻了59.49%。這個比例反映的邏輯是，信貸專家們把“基礎資產質量”“資產持有人信用”“債券評級高低”作為首先考量的風險，而這三項都是圍繞資產證券化過程展開。這是由我國目前的金融環境、法律環境、銀行偏好共同決定的。

5.2 林業第一、第二、第三產業資產證券化風險隸屬度計算結果

表5 林業第一產業ABS風險測度隸屬度

表6 林業第二產業ABS風險測度隸屬度

表7 林業第三產業ABS風險測度隸屬度

5.3 模糊綜合評價數據討論

模糊綜合評價數據顯示，林業第一產業風險評價得分3.67796分，在41.25%程度上隸屬于較高風險，在34.59%程度上隸屬于中等風險。這主要源于兩個原因：其一，林業第一產業參與主體的市場化程度較低，資產很大程度上依賴于國家政策性金融支撐，商業銀行雖可介入但很難有平等的議價地位；其二，現有商業銀行介入林業第一產業的方式主要以“信貸資產證券化”為主，這種模式類似于間接的“資產收益權轉讓”，因此商業銀行較為謹慎。林業第二產業風險評價得分3.11611分，在43.03%程度上隸屬于中等風險，在36.25%程度上隸屬于較高風險。這主要源于林產品銷售價格波動性大、林產品替代成本較低、應收賬款難辨真偽。相對于林業第一產業，信貸專家對林業第二產業有更多的寬容空間。林業第三產業風險評價得分2.65869分，在43.41%程度上隸屬于中等風險，在35.27%程度上隸屬于較低風險。林業第三產業是面向消費者，市場化程度很高，屬于可預期現金流明確的朝陽產業。

6 結論和政策建議

6.1 結論

本研究基于AHP層次分析法和模糊綜合評價法得出以下結論：①在全部分析指標中，“證券化風險”“信用風險”“銀行內部風險”“環境風險”是林業產業資產證券化最主要的風險。②在林業三個產業中，林業第一產業資產證券化隸屬偏較高風險，林業第二產業資產證券化隸屬中等風險，林業第三產業資產證券化隸屬中等偏較低風險。③從更容易盤活林業資產，更容易促成銀行投資角度，銀行要優先發展林業第三產業資產證券化，適當發展林業第二產業資產證券化，審慎發展林業第一產業資產證券化。

6.2 政策建議

上述研究結論具有重要的政策含義。于林業企業而言，獲得了一個極好的審視自身資產價值和融資可能性的窗口；于銀行而言，在“資產管理-投行管理-財富管理”的金融創新之下，亟待轉變思維，更多地從“資產”角度而非“企業”角度挖掘商機。林業產業是一個橫跨三大產業的復雜系統，資產證券化也是一項復雜的工程，但“盤活資產”“互利共贏”的理念將兩者慢慢拉攏在一起。從微觀方面，林業產業資產證券化能否從理論走向實踐，主要在于林業產業能否滿足當下銀行普遍的信貸風險偏好，商業銀行更加關注“林業資產現金流穩定性”“林業資產權屬人信用”和“林業證券化資產債券評級”。宏觀方面，商業銀行更愿意投資市場化程度高、透明度較高、流動性較好的資產。相對比而言，林業第三產業有著巨大的發展潛力，特別是森林生態公園的門票收入會成為一類“未來收益權”類的優質資產。林業企業要抓住機遇，主動利用好森林資源發展第三產業，盤活林地存量。