壓力襪壓力與位移隨著裝時間變化的有限元模擬

鄭玉婕, 覃 蕊

(青島大學 紡織服裝學院,青島 266071)

壓力襪是日常生活中應用非常廣泛的服飾之一[1-3]。在穿著壓力襪的過程中,壓力襪的功能與著裝壓力舒適性有著密切聯系[4]。目前,關于壓力襪的研究大多集中于足踝部壓力研究,對于襪口處壓力研究較少。襪口是影響壓力襪舒適性和功能性的重要部位,壓力過小襪口處容易滑脫,壓力過大會使穿著者產生不適感,同時給肌體帶來負面影響,甚至產生器官與組織病變[5]。因此,壓力襪的襪口處應具有適宜的壓力分布趨勢及壓力范圍。

對于壓感舒適性的評價,傳統方法是直接測量人體受壓部位壓力數據,再結合主觀評價進行綜合測評[6]。該方法雖然操作簡單,但由于受到人的生理和心理因素的影響,容易使實驗結果產生偏差[7]。Verillo[8]指出,在理想狀態下,低于1 μm的體表位移就能有效引起壓感的產生。該結果表明,人體由于壓力而產生的內向位移是壓感舒適性評價的有效指標。壓力襪襪口對人體施壓,人體會產生相應的內向位移,不同部位的位移存在差異。同時,隨著著裝時間的延長,襪口處人體所受壓力及位移也呈現不斷變化的趨勢。深入探討人體穿著緊身服裝過程中壓力與位移之間的關系,對于壓感舒適性評價及服裝的結構優化改良具有一定的參考意義。

本研究以壓力短襪為研究對象,通過非接觸式三維人體掃描獲取襪口處人體腿截面形態,針對壓力短襪襪口處存在的壓力過大導致不舒適感或壓力過小產生的易滑脫等壓力分布不合理現象,結合壓力襪的著裝時間,將著裝過程分為6個時間段(瞬時,1、2、4、8、12 h),應用ANSYS有限元軟件模擬6個時間段襪口處人體腿截面壓力與位移分布趨勢。通過曲線擬合,得到6個時間段壓力、位移與對應角度的函數關系。即:當人體處于服裝壓力狀態時,在已知壓力值的前提下,可通過函數方程計算人體對應的位移值,進而為壓感舒適性評價提供數據支撐。該方法為壓力襪襪口處的壓感舒適性研究及優化設計提供了理論參考,同時可應用于其他類型的緊身服裝。

1 壓力襪襪口處人體腿截面曲線的確立

1.1 非接觸式三維人體掃描

準確的人體形態結構是進行人體壓力及位移形變研究的基礎,基于此,本研究通過非接觸三維人體掃描獲取壓力襪襪口處人體腿截面形態結構。

通常壓力短襪襪口位置為人體內側腳踝點水平向上5～6 cm處[9],而5 cm和6 cm處截面大小及形狀基本相同,本研究將6 cm處定義為襪口截面位置。

1.1.1 實驗對象

選取年齡在20～25歲標準體型的健康男性大學生50人。

1.1.2 實驗對象選取原則

參照GB 10000—1988《中國成年人人體尺寸》國家標準,實驗對象的平均身高和體重與95%的標準中統計數據相似[10]。

1.1.3 實驗要求

受試者赤裸腿部站在TecMath非接觸式三維人體測量儀上,通過三維人體掃描,把50位受試者內側腳踝凸出點水平向上6 cm處截面形態掃描并截取出來。圖1為隨機選取的襪口處腿截面掃描曲線。

圖1 襪口處人體腿截面曲線Fig.1 Leg cross section of the top part of socks

1.2 襪口處腿截面形態的獲取

剔除不符合標準的截面曲線,本研究選取其中的40個截面進行處理。將40條曲線同心疊加,圓心為截取截面曲線時三維掃描系統自動定義的圓心。用Matlab軟件按照直角坐標系每5°為一點等分,分別確定40個截面曲線中72個點的坐標,再將40個截面坐標的各對應點分別取平均值,即得到平均腿部截面圖及各點坐標值(圖2)。

圖2 襪口處腿截面形態Fig.2 Shape of the leg cross section at the top part of socks

2 實驗樣品的選取及壓力測試

2.1 實驗樣品的選取

考慮到市面上常用壓力短襪的面料成分組成,本研究選取了6款常見的壓力短襪作為實驗樣品,并將6款樣本根據面料成分劃分為兩組,襪口部位具體參數如表1所示。

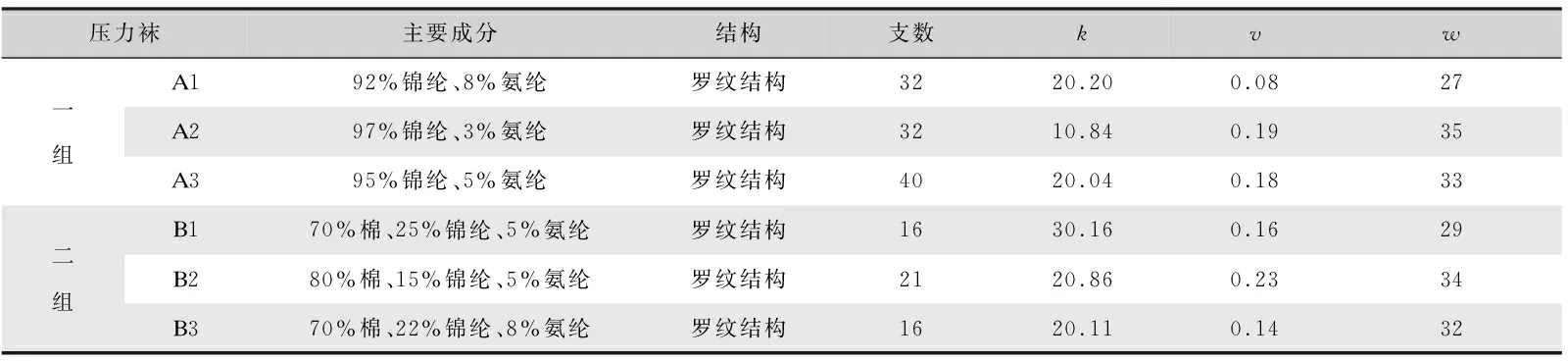
表1 6款實驗用壓力短襪性能參數Tab.1 Detailed parameters of six experimental socks

其中,A1、A2、A3主成分為錦綸,B1、B2、B3為棉;k(N/m)為襪口彈性系數,v為襪口材料泊松比,w(mm)為原始襪口寬。

2.2 壓力測試

本研究使用AMI3037-5S氣囊式服裝壓力測量裝置(日本AMI公司),測量受試者穿著6款實驗用壓力襪時襪口處72點壓力值。

通常情況下,人一天中連續穿著壓力襪的時間不超過12 h。基于此,本研究定義連續穿著壓力襪的最長時長為12 h,并將著裝時間劃分為6個時間點:瞬時壓力,1、2、4、8、12 h,通過壓力測試分別得到6款壓力襪襪口處72點壓力數據。

本研究以A1為例,壓力數據如圖3所示。

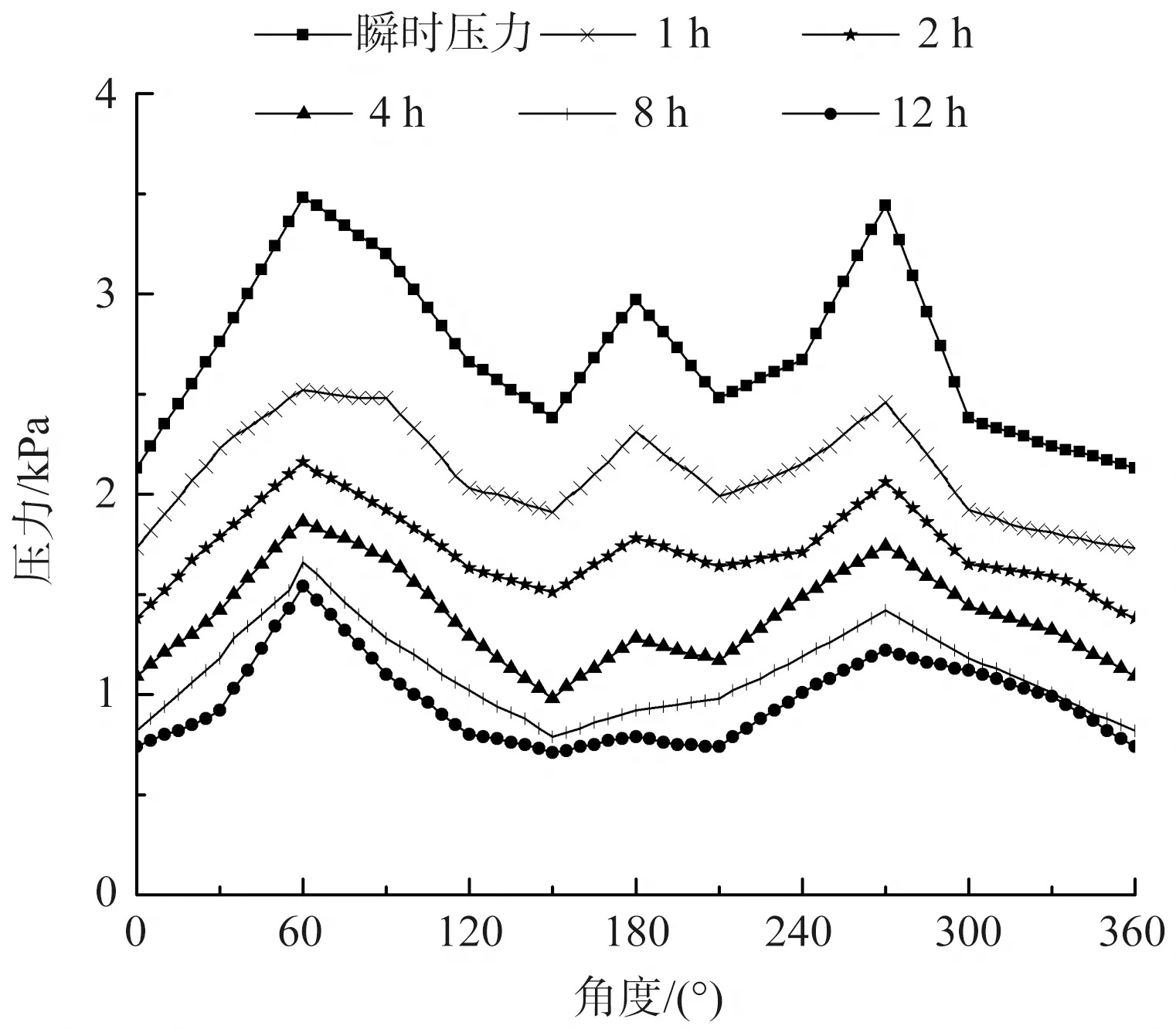
圖3 不同時間段壓力值(A1)Fig.3 Pressure values in different periods (A1)

由圖3可見,襪口處人體腿截面上所有點的壓力值隨著著裝時間的延長均呈現遞減趨勢。在著裝過程中,60°和270°位置壓力較大,0°位置壓力較小。在瞬時壓力中,270°壓力值為3.44 kPa,0°壓力值2.73 kPa。穿著壓力襪1 h后,270°壓力值下降為2.46 kPa、下降幅度28.49%,0°壓力值1.73 kPa、下降幅度18.78%。可見,在穿著壓力襪1 h內,腿截面上原始壓力越大的位置,壓力數值隨著著裝時間的延長下降越明顯。穿著12 h后,270°壓力值下降為1.22 kPa、下降幅度64.53%,0°壓力值0.74 kPa、下降幅度65.26%,表明隨著著裝時間的延長,壓力下降幅度趨于平衡。同時,隨著著裝時間的延長,壓力值的下降幅度越來越小,著裝后8 h和12 h的壓力數據已基本近似。因此可以近似地認為,著裝8 h后,襪口處截面上各點壓力值基本達到平衡,不同點的壓力數值差距逐漸縮小。

3 襪口處腿截面有限元模型的構建

人體小腿截面主要由皮膚、軟組織(肌肉、血管、神經)、脛骨和腓骨組成[11],襪口處人體腿部皮膚厚度約為1.5 mm[12]。根據非接觸式三維人體掃描及人體小腿處內部結構,本研究構建襪口處人體腿截面有限元模型,如圖4所示。

圖4 襪口處截面有限元模型Fig.4 FE model of leg cross section of the top part of socks

本研究將人體視為彈性體,腿截面與壓力襪間的接觸為彈性接觸。假設襪口處人體皮膚、軟組織及骨骼均為各向同性均勻的線彈性材料,分別設置三種材料的單元類型、彈性模量和泊松比,詳細參數如表2所示。

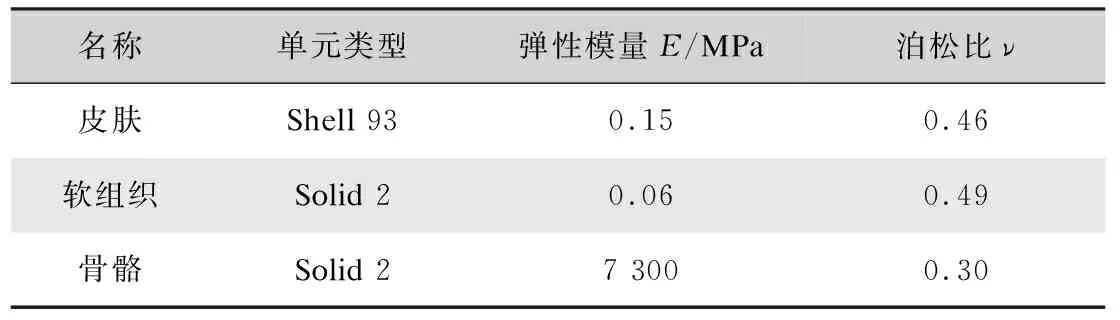
表2 有限元模型的單元類型及材料參數Tab.2 Element type and material parameters of FE model

對襪口處腿截面進行二維三角形網格劃分,同時施加壓力載荷。骨骼為人體腿截面中最硬的部位,當穿著壓力襪后,可以近似地認為脛骨和腓骨在受壓后不發生位移。基于此,本研究將脛骨和腓骨X、Y方向位移均為0作為模型的邊界條件。

4 著裝后腿截面位移的有限元模擬

4.1 襪口處腿截面受壓后位移模擬

在ANSYS有限元軟件中導入腿截面壓力值作為壓力載荷,通過求解和后處理,可得到6款壓力襪襪口處腿截面位移分布云圖。本研究以穿著實驗用樣品A1一小時為例,位移分布云圖如圖5所示。

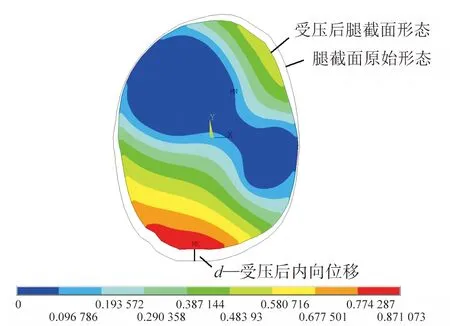
圖5 著裝1 h后位移分布云圖(A1)Fig.5 Displacement distribution cloud chart of leg cross section after 1h (A1)

圖5中,不同顏色代表不同的位移大小,下面的顏色帶從左到右表示數值依次增加。

4.2 位移隨著裝時間變化趨勢分析

通過有限元模擬,可得到6款實驗用壓力襪在6個時間段72點各自位移。本研究以A1為例,位移隨時間變化數據如圖6所示。

圖6 位移隨著裝時間變化曲線(A1)Fig.6 Graph of the displacement values with time (A1)

由圖6可見,隨著著裝時間的延長,腿截面上各點位移均呈遞增趨勢,且6個時段的位移分布規律基本近似。270°位置為位移最大點,0°位置為位移最小點。在最開始的1 h內,位移的增長幅度最大,約為總體增長幅度的1/3;4 h后,位移增長幅度基本達到整體增長幅度的1/2;而后隨著時間的延長,增長幅度越來越小。在穿著壓力襪12 h后,位移最大點由原始狀態的1.178 mm增至4.44 mm,增長了3.77倍,位移最小點處由原始狀態的0.11 mm增至0.41 mm,增長了3.73倍,且同一時段的位移最大值約為位移最小值的2倍。

4.3 襪口處腿截面壓力與位移函數關系

當人體受到服裝壓力時,壓力與體表產生的內向位移之間的關系是評價壓力舒適性及對緊身服裝進行優化設計的關鍵。為了探討壓力襪整個著裝過程中壓力與位移間的函數關系,本研究構建了“壓力/位移—角度”函數曲線,如圖7所示。

由圖7可見,6組曲線幾乎呈現出相同的變化趨勢,最高點約出現在350°位置,最低點約出現在255°位置。曲線分布的總體趨勢為[50°,135°]和[255°,350°],數值呈現遞增趨勢,而[0°,50°][135°,255°]和[350°,360°]遞減。從圖7還可以看出,無論穿著何種類型的壓力襪,且無論著裝時長如何,相應位置的“壓力/位移—角度”函數關系基本保持不變。該結論為確定壓力襪襪口處壓力舒適范圍提供了可能,也為人體體表位移數據的獲取提供了參考依據。

圖7 著裝過程中“壓力/位移—角度”函數曲線Fig.7 Functional curve between pressure/displacement ratio and angle in whole wearing process

為了更加準確地對函數曲線進行擬合,本研究根據曲線趨勢對函數曲線進行了轉換,角度由[0°,360°]轉換為[-10°,350°],如圖8所示。

圖8 “壓力/位移—角度”函數曲線角度轉換Fig.8 Conversion curve of pressure/displacement ratio and angle functional curves

根據曲線分布趨勢,本研究將函數曲線分為兩個區域,分別為[-10°,135°](第一部分)和[135°,350°](第二部分)。通過Origin軟件分別擬合兩條“壓力/位移—角度”二次曲線,擬合曲線及方程如圖9所示。

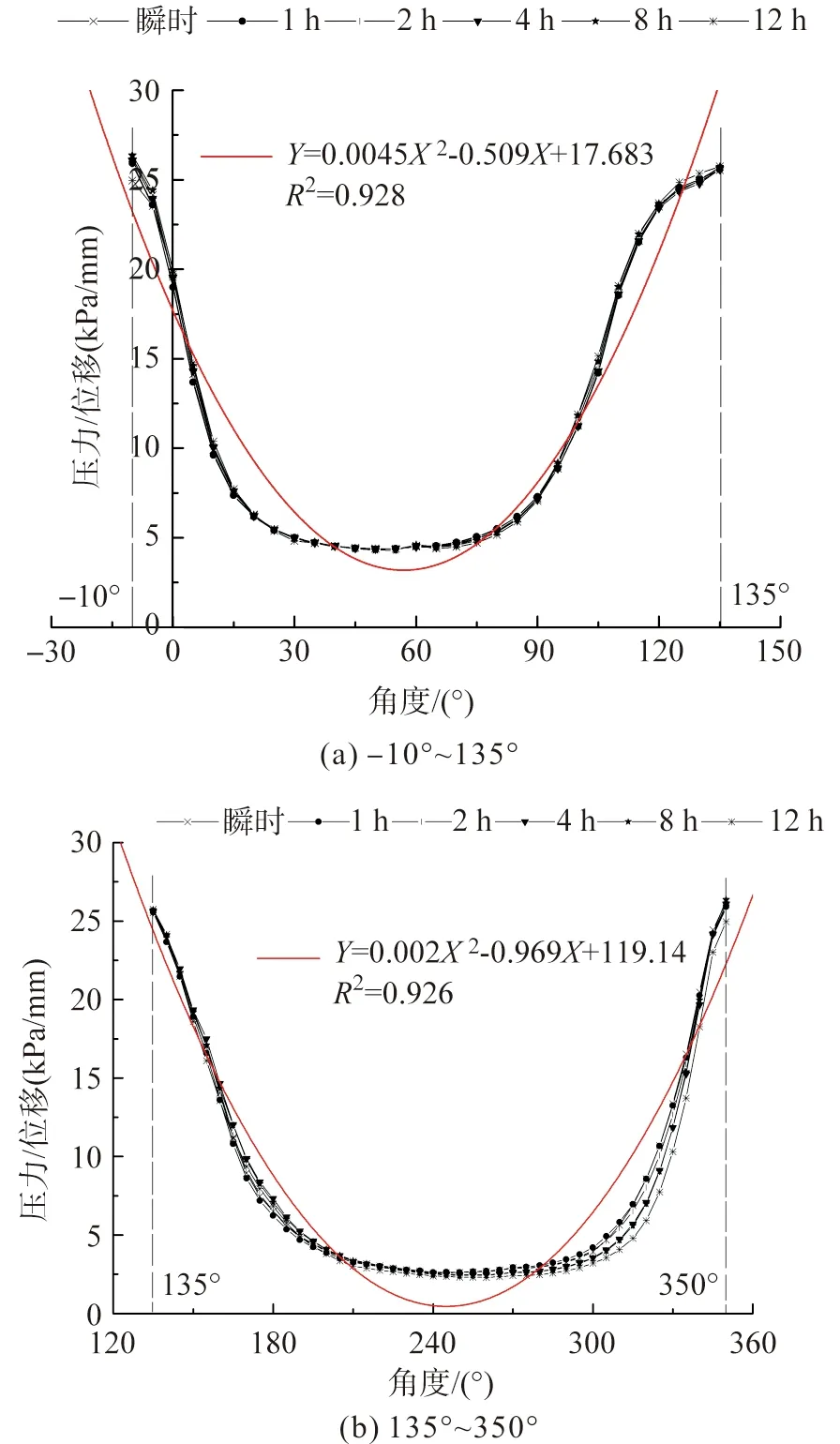
圖9 “壓力/位移—角度”二次曲線擬合方程Fig.9 Fitting curve of functional relationship between pressure/displacement ratio and angle

在圖9中,角度為自變量,“壓力/位移”為因變量,擬合曲線為二次方程。擬合曲線方程式及擬合度如表3所示。

表3 擬合曲線方程Tab.3 Fitting curve equations

表3中,兩條擬合曲線的擬合度(R2)均在0.92以上,顯示擬合度良好。根據擬合曲線方程,可以獲取人體位移數據及任意點壓力與位移之間的關系。由外部壓力產生的垂直于人體體表的內向位移是評價緊身服裝壓力舒適性的關鍵指標。但是,由于緊身服裝對人體產生的壓力有限,因此位移形變通常較小,并且難以使用常規的物理方法獲取較為準確的人體位移值[13-15]。利用本研究獲得的擬合曲線方程,想要獲取人體腿截面上任意點的位移數據,只需要應用壓力測試系統測量出該點壓力值,將壓力值和角度值代入文中求得的二次方程,即可求出該點對應的位移值。

4.4 襪口處腿截面面積縮量分布趨勢

人體體表面積縮量是評價緊身服裝壓力程度的重要指標。根據腿截面面積縮量的分布趨勢,在襪子設計過程中,可以將襪口設計為松緊不同的區域,以滿足人體的著裝舒適性需求。為了獲取人體著裝后腿截面的面積縮量分布情況,本研究將腿截面上72點中的每四個相鄰點構成一個不規則四邊形。假設四個相鄰點的坐標值為Mn(Xn,Yn)、Mn+1(Xn+1,Yn+1)、Mn′(Xn,Yn)、Mn+1′(Xn+1,Yn+1),該四邊形為面積Sn,可以近似地認為Sn的面積等于襪口處腿截面不規則四邊形面積Sn′(圖10)。

(1)

為了更加準確地判斷壓力作用下腿截面面積縮量的分布趨勢,本研究將襪口處腿截面按照每30°為一個區域等分為12個區域,[0°,30°]為區域1,[30°,60°]為區域2,……,以此類推。依據式(1)分別計算12個區域在不同著裝時間段(瞬時,1、2、4、8、12 h)的面積縮量數據,如圖11所示(以A1為例)。

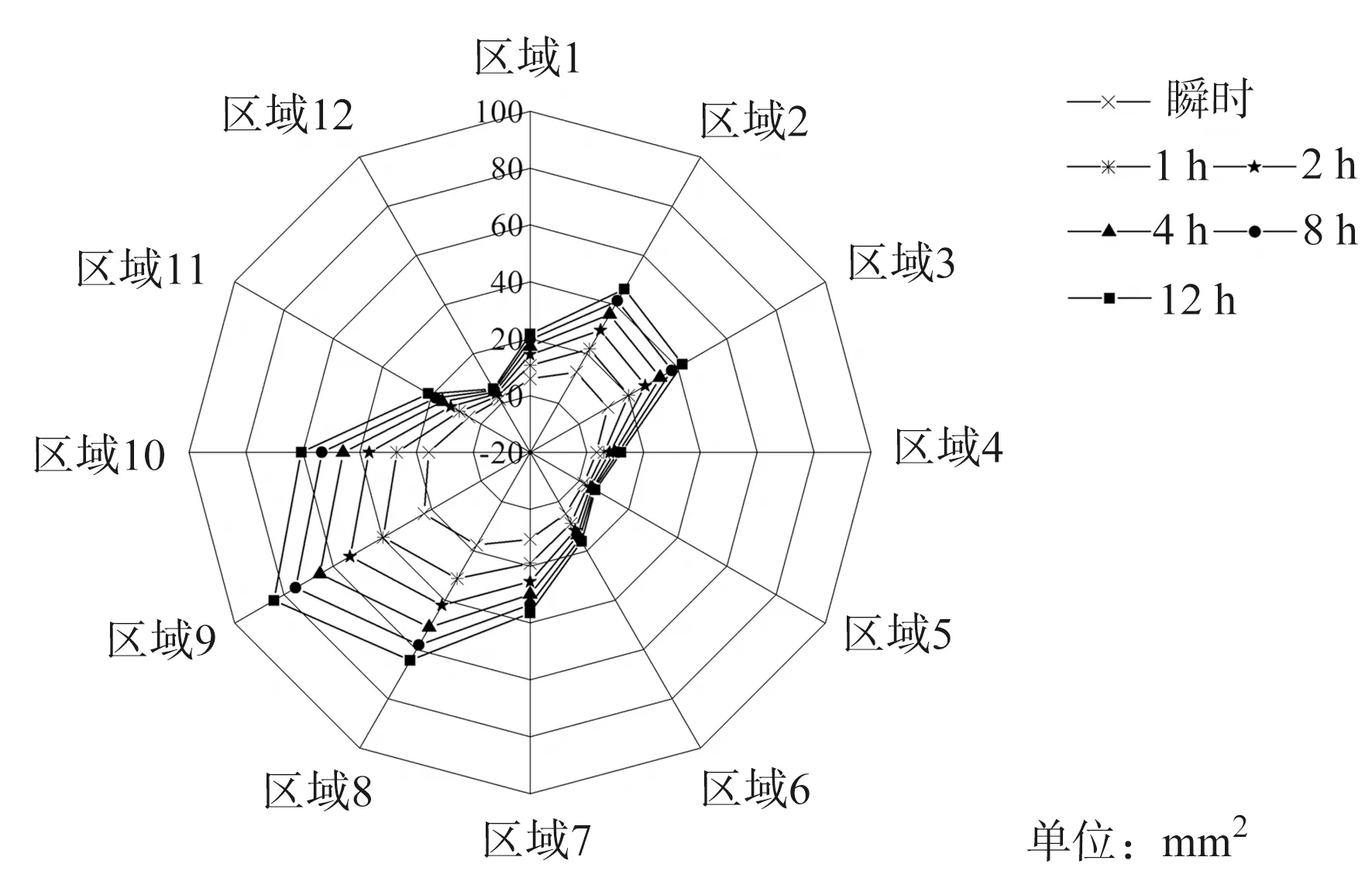
圖11 腿截面6個時間段面積縮量(A1)Fig.11 Area shrinkage mass of the lower leg at six periods of time (A1)

由圖11可見,12個區域的面積縮量均隨著裝時間的延長呈現增長趨勢。在6個時間段內,區域9在整個著裝時間內面積縮量最大,區域5最小,區域12與區域5幾乎相同。區域9的面積縮量約為區域5和區域12的15倍。穿著壓力襪12 h后,區域9面積縮量增加3.63倍,區域5和區域12約增加3.48倍。由于區域5和12位置有脛骨和腓骨,軟組織層較薄,在一段時間的壓力作用下,腿截面位移達到平衡。因此,隨著著裝時間的延長,區域5和區域12的面積縮量增加略小于其他區域。另一方面,在軟組織層較厚的區域9中,當其他參數相同時,腿截面位移變化較大。

在壓力襪的設計過程中,可以根據面積縮量的分布趨勢,結合主觀壓力舒適性評價,將襪口設計為松緊不同的區域,以滿足人體的著裝舒適性需求,該結論為壓力襪襪口優化設計提供了參考。

5 結 論

緊身服裝對人體體表產生的位移是評價壓感舒適性和進行服裝結構優化的重要指標。通常情況下,緊身服裝產生的人體形變較小,并且很難通過常規物理方法獲取位移數據。本研究提供了一種準確、簡單可行的方法獲取人體穿著緊身服裝后的位移數據。

1) 以彈性壓力襪為研究對象,在已知人體小腿處各部位的相關物理參數及壓力襪口對人體腿部施加的部分點壓力數據的前提下,將壓力襪的著裝過程分為6個時間段(瞬時,1、2、4、8、12 h),通過非接觸式三維掃描、襪口處腿截面模型的建立、有限元模擬和曲線擬合,得到了在穿著6款壓力襪時“壓力/位移”與角度之間的函數關系。

2) 無論受試者穿著何種壓力襪,著裝時長如何,“壓力/位移”與角度之間的函數關系基本保持不變。利用該擬合曲線方程,在已知壓力值的情況下,可以得到襪口處腿截面任意角度點、穿著壓力襪后任意時長的位移數據。

3) 在壓力襪的設計過程中,可以根據壓力、位移與角度之間的關系,將襪口設計為松緊不同的區域,以滿足人體的著裝舒適性需求,該結論為服裝壓力舒適性的評價和服裝結構優化改良提供了參考。此方法同樣適用于其他類型的緊身服裝。

《絲綢》官網下載

中國知網下載