一種基于改進天牛須探索算法的多點定位算法

甄 然，王振博，闞海龍，倪永婧

(1.河北科技大學 電氣工程學院,河北 石家莊 050018;2.河北科技大學 信息科學與工程學院，河北 石家莊 050018)

0 引言

隨著經濟社會及人工智能的發展，定位的重要性越發得到展現。而在定位中，即使是衛星定位，算法也是當之無愧的重中之重。因此，越來越多的研究者對定位算法進行研究與改進，得到了許多創造性的成果，比如Chan-Taylor聯合算法[1-2]和WiFi定位[3]等。

智能優化算法的提出，為一系列復雜問題的解決提供了思路。智能優化算法對目標函數和約束的連續性與凸性沒有任何要求，有時連有沒有解析表達式都不要求，對計算中數據的不確定性也有很強的適應能力，因此受到研究者的喜愛，將粒子群算法[4]和卡爾曼濾波算法[5-6]等優化算法與定位算法進行融合，進而對目標進行定位。

天牛須探索(Beetle Antennae Search,BAS)算法是2017年提出的一種生物啟發的智能優化算法[7]，是利用天牛覓食原理啟發而開發的算法，適用于多個領域的問題優化[8-13]，同時該算法也可以與多種優化算法進行融合，比如遺傳算法[14]和神經網絡[15]等，從而改善收斂性，提高優化性能。

在定位領域，由于天牛自身大小的原因，BAS算法如果不進行改進則不適用于大空間遠距離定位，因此大部分研究者運用BAS算法進行室內短距離的定位，鄒東堯等[16-17]將BAS算法與RSSI算法進行結合，提出運用BAS優化的室內定位算法，劉影等[18]提出普適的基于天牛須尋優的室內定位算法。

Chan算法作為基本的TDOA定位算法，雖然有著在非視距環境下定位誤差較大的缺點，但是由于其經濟性強、非常適合工程實際，一直以來都被進行研究，如魏振婷等[19]提出的基于自適應誤差模型的改進Chan算法。

大多數研究針對某種算法的優化時采用的是結合另一種優化算法，而未能對該算法進行深入研究，或者是僅對算法進行數學上的改進但卻未能結合實際。對此，針對BAS算法因為天牛自身大小不能在遠距離定位中應用的問題，本文對BAS算法本身進行了結合定位實際的適當的改進，提出了一種基于Chan算法的改進BAS算法。

本算法具有以下幾個優勢：

① 通過將大空間遠距離的定位轉換為小空間近距離的定位，可以將原本僅僅適用于室內近距離定位的算法(如BAS算法)應用于遠距離定位[20]。

② 因為BAS算法收斂速度快，因此本算法運行時間較短，并且可以較好地定位目標點。

③ 增加了一個對步長的選擇過程，與卷積神經網絡的訓練過程相似[21]，可以選取合適的步長來對目標點進行定位，準確度更高。

④ 本文選擇的2種不同精度的定位算法為Chan-Taylor算法和卡爾曼-Chan算法，經過改進的BAS算法具有一定的普適性，初始的2種不同精度的定位算法可以是任何2種算法，初始定位算法越精確，最終的結果也會越精確。

1 Chan算法

Chan算法是一種基于TDOA技術，具有解析表達式解的定位算法。該算法可以分為2部分：第一部分是利用待定點到各個基站與待定點到達參考基站的時間差求出各個基站與待定點相對于參考基站的距離差；第二部分是利用這些距離差，采用最小二乘法進行定位。Chan算法的具體步驟如下。

由于定位時常是在三維環境下進行的，因此對三維環境下的定位進行分析，三維環境下的基站系統如圖1所示。

圖1 三維環境下的基站系統Fig.1 Base station system in 3D environment

用方程對圖1進行描述：

(1)

式中，(x,y,z)為目標位置；(xi,yi,zi)為地面站坐標；Ri為目標點到第i站間的距離；Ri,1為目標點到達主站與第i副站間的距離差；c為無線電磁波傳播速度；τi,1為飛機發出的信號到達主站與第i副站間的時間差。

對于求解式(1)中的未知量，當基站數量大于維數與1的和時，可以利用加權最小二乘(WLS)法進行求解。而Chan算法利用將R1視為已知量，則式(1)為x,y,z的線性方程，經過計算，求得：

(2)

將式(2)代入R12=(x-x1)2+(y-y1)2+(z-z1)2中，整理得到：

(3)

當N2-4MK=0時，即R1解唯一，定位有效，且目標位置唯一。

當N2-4MK>0時，R1有2個解，如果2個解一正一負，取正解作為R1的真實值；如果同為正或同為負，即存在模糊解，則需要根據其他條件進行判定。

當N2-4MK<0時，無解，定位不能實現。

求解出R1的值后，根據R1的方程和BSi坐標就可以求得目標T(x,y,z)的值。

Chan算法的定位原理如圖2所示。

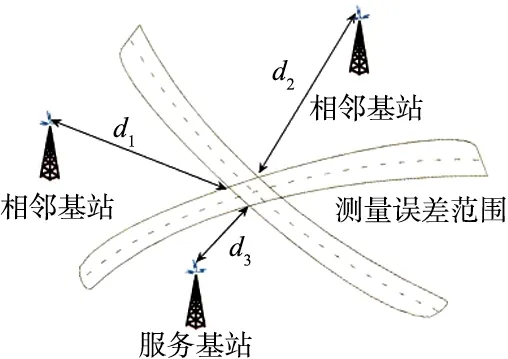
圖2 Chan算法的定位原理Fig.2 Positioning principle of Chan algorithm

d1,d2,d3分別為目標點到各個基站之間帶有誤差的距離，由于誤差的存在，實際計算所得到的是2條帶狀區域的重合部分。

Chan算法的簡潔十分適合工程實際，因而一直被廣泛研究。本文基于Chan算法，利用2種不同精度的Chan算法，結合2017年提出的BAS算法，提出基于Chan算法的改進BAS定位算法，將原本僅適用于短距離定位的BAS算法應用于遠距離定位。

2 基于Chan算法的改進BAS算法

2.1 BAS算法

BAS算法是2017年提出的生物優化算法，該算法的原理是天牛在搜尋食物的過程中，根據左右兩須探測到氣味的強弱程度進而決定向左還是向右前進，并最終找到整個區域內氣味最濃的點。針對BAS算法，結合Chan算法和TDOA思想，對BAS算法進行改進，使其能夠更好地適應大空間定位。BAS算法概述如圖3所示。

圖3 BAS算法概述Fig.3 Overview of BAS algorithm

根據BAS算法原理，建立天牛模型，模型如下所示：

① 確定天牛的初始位置：與當前多數的隨機給定初始位置的方式相比，為了減少無用的探索，改進的BAS算法采用Chan-Taylor算法對目標點進行一次定位，并將該點定為天牛的初始位置Q。同時,確定天牛左右兩須的位置坐標:

(4)

式中,Xl為天牛左須的坐標;Xr為天牛右須的坐標;d0為天牛須的長度;t為天牛的方向向量。

② 通過適應度函數p獲取左右兩須的函數值，并朝著對應須的方向進行移動。比較p(Xr)與p(Xl)的大小。若p(Xr)>p(Xl)，則天牛向著右須方向行進步長step;反之，天牛則向左須方向行進步長step。

③ 按照上面的步驟進行迭代，直至找到目標函數W值最優的點，即為目標點。

BAS算法的流程如圖4所示，本文針對其中的部分步驟進行改進。

圖4 BAS算法流程Fig.4 Process of BAS Algorithm

2.2 對初始位置的改進

當前,多數優化算法對于初始位置采用的是隨機賦值的方式，對于原始的BAS算法，針對初始位置同樣采用的是隨機賦值方式。但是這種方式下，在增加全局探索的同時，增加了較多對無用區域的探索。在數學上，增加全局搜索能力對最終結果的確定有著極大的好處，但是在定位領域，真正有用的探索區域是目標點附近的區域。初始值設在目標點附近與設在遠離目標點的位置，對算法的后續迭代會有很大的影響。人是通過參照物來確定自身的，定位同樣如此，通過把初始位置作為參照物或參考點，能夠使其移動更加準確。

因此，改進的BAS算法采用一次定位的方式來確定天牛的初始位置。通過對目標點進行一次定位，并將該點定為天牛的初始位置Q。通過一次定位，減少天牛對無用區域的探索。以二維平面為例，對于天牛初始位置，經過一次定位所確定的初始位置距離目標點相對較近，而采用隨機設定方式所確定的初始值距離目標點相對較遠。探索范圍對比如圖5所示，在40 000 m×20 000 m的平面進行定位，若設中心點為目標真實位置，則經過一次定位所確定的范圍可以用內部圓來進行表示，而隨機賦值所確定的范圍則為外部圓所表示的區域。很明顯，經過一次定位后，算法的無效探索范圍得到極大程度的減小，相對的，算法運行時間和準確度等也會得到一定程度的提高。

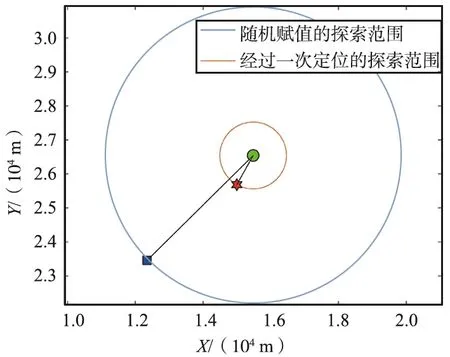
圖5 探索范圍對比Fig.5 Comparison of exploration areas

2.3 對位置更新公式的改進

BAS算法的位置更新式為：

A=A+step×(-1)×t×sign(p(l)-p(r))+

0.05×rand(1)。

(5)

改進的BAS算法的位置更新式為：

A=A+(step/cos(θ))×(-1)×t×

sign(p(l)-p(r))+0.05×rand(1)，

(6)

式中，t為天牛的行動方向，由初始隨機設定；p(l)和p(r)為左右兩須的適應度函數；A為天牛的位置；θ為天牛當前位置與一次定位點之間的夾角。

假設天牛的初始位置為A，迭代次數為(n1+n2)，其中朝左移動n1次，朝右移動n2次，每次移動的步長為step，運用BAS算法的最終結果為：

A=A+step×t×(n2-n1)。

(7)

運用改進的BAS算法的最終結果為：

A=A+step×t×[(cos(θa1)+…+cos(θan2))-

(cos(θb1)+…+cos(θbn1))]，

(8)

式中，a1,a2,…,an2為向右移動的次數；b1,b2,…,bn1為向左移動的次數。

相對于原始的BAS算法，經過改進后，每次移動的距離隨著角度的變化而隨時變化，避免了BAS算法初始步長因子隨機設定而造成的移動距離與實際不適應的問題，增強了算法的自適應能力，也可以避免采用時變步長造成探索區域不適應的問題。

對式(7)進行分析，若n2=n1，則經過(n2+n1)次迭代后，天牛相當于未移動，導致定位失敗，但是經過改進后，如式(8)，由于角度在實時變化，即使n2=n1，天牛的最終位置也會有所變化。

2.4 對步長的改進

根據對BAS算法的理解可以得出，假設天牛的初始位置為A，迭代次數為(n1+n2)，其中朝左移動n1次，朝右移動n2次，每次移動的步長為step，則天牛的最終位置為：

A+step×t×(n2-n1)。

(9)

因此，對于BAS算法，影響其定位精度的因素可以分為3部分：迭代次數、初始位置和每次移動步長。其中，初始位置由一次定位確定，誤差一定，所以主要影響因素是迭代次數和每次移動的步長。

BAS算法的迭代次數一般為20，因此主要考慮步長的影響。

對于步長，基于對卷積神經網絡訓練行為的理解，對改進的BAS算法采用增加一個對于移動步長的訓練部分的方式，借鑒卷積神經網絡通過訓練集來對整個網絡進行訓練即可使網絡逐漸適應實際情況的思想，選取多個步長，對于一個在2次定位結果范圍內的訓練點進行定位，找到適合的步長，再對目標點進行定位。

當前，有研究者提出采用時變步長的方式，就是隨著迭代次數的增加步長逐漸減小，此步長變化方式在定位領域可能會造成探索區域減小的問題，進而影響定位精度，且步長與迭代次數之間的變化關系隨著定位地點和天牛初始位置等一些其他因素的不同，會有一定的變化，確定步長和迭代次數二者關系較為復雜。

步長的大小決定算法探索的密度，與初始值結合在一起決定算法的探索區域。優化算法本質上是對探索區域內的盡可能多的點進行驗證，但是這并不意味著步長越小越好。步長的選擇要與初始值一起考慮，即：

K=f(A,step)，

(10)

式中，f為一個未知的函數關系，且在一定范圍內該函數關系可以認為不變。正因為如此，通過對2次定位確定的范圍內的一個確定點進行訓練定位，可以通過對該點的定位確定f的關系，進而選擇出適合的步長對目標點進行定位。

2.5 改進BAS算法步驟

綜上所述，改進BAS算法的具體流程如圖6所示。

圖6 改進BAS算法流程Fig.6 Process of improved BAS algorithm

3 基于Chan算法的改進BAS定位算法的定位流程

遠距離定位時，采集到的數據有一定程度的非視距誤差，因此首先利用卡爾曼濾波的方式，適當降低該誤差對定位的影響。然后，利用2次定位的方式，對目標點進行范圍定位，將目標點確定到一定的范圍中，同時，對天牛的初始位置進行賦值，而不是采用隨機賦值的方式對天牛的初始位置進行賦值。這樣可以降低系統對無用區域的探索，同時也可以避免對某些區域進行探索時陷入局部最優的情況。

利用2種不同精度的Chan算法對目標點進行定位，將其中一個結果作為待定點的一次定位結果Q，將另一個結果作為天牛的初始位置A，這樣可以將大空間遠距離定位轉換為小空間近距離定位。然后，利用BAS算法，進行優化，待定點的具體位置就是天牛要尋找的食物。假設在整個定位區域內共有n個基站對該目標進行定位。

該算法的目標函數W為：

(11)

式中，(Qx,Qy)為一次定位點Q的坐標；(x,y)為經過BAS算法的最終結果，直至迭代結束，找到目標函數值最小的點，即為所求。同時，該算法的適應度函數p為：

(12)

式中，h為一次定位點到各個基站與到參考基站之間的距離差；s為天牛左須和右須各自到各個基站與到參考基站之間的距離差。

基于Chan算法的改進BAS定位算法定位的具體步驟如下：

步驟1 利用TOA的方式采集數據。

步驟2 根據接收到的信號對目標點進行2次定位，將其中一個結果作為待定點的一次定位結果Q，將另一個結果作為天牛的初始位置A，確定目標點的大致范圍。同時，在該范圍內隨機選擇一個點作為訓練點，然后,對訓練點進行二次定位，為訓練過程做準備。

步驟3 首先改進BAS算法的位置更新公式。在k維空間中，待定點的初始方向用一個矩陣t表示，本文中，將該矩陣設為t=[1,1，…]，即將天牛的初始方向始終設置為朝著各軸的正方向。同時，根據天牛自身的特點，寫出其左右兩須的坐標方程：

(13)

式中，A為天牛的初始位置，由步驟1所得，是[x,y，…]，由所需探測空間的維數確定；d0為天牛左右兩須之間固有的距離；A1與Ar分別表示天牛左右兩須的坐標。根據左右兩須各自的適應度函數和一次定位點Q,求出左右兩須的適應度函數值，然后確定天牛下一步的行動，確定天牛的位置方程為：

A=A+(step/cos(θ))×(-1)×t×

sign(p(l)-p(r))+0.05×rand(1)，

(14)

式中，p(l),p(r)，分別為關于左右兩須的適應度函數；θ為一次定位點與天牛主體之間的夾角，用來調整天牛的移動方向。

步驟4 訓練改進的BAS算法，找到最優步長。具體方式為選取多個步長，再根據訓練點的2次定位結果，采用改進后的BAS算法對該點進行定位，找到最優步長。

步驟5 將找到的最優步長帶入到改進后的BAS算法中，對目標點進行定位。

改進BAS算法定位的具體流程如圖7所示。

圖7 改進BAS算法定位的具體流程Fig.7 Specific process of improving the positioning of BAS algorithm

4 仿真分析

為了驗證該算法的準確性及對定位結果的優化，使用Matlab 2019a對該算法進行仿真實驗。誤差選用均值為10的高斯白誤差。

4.1 算法改進前后的性能分析

4.1.1 初始位置的改進

對于初始位置的選擇，仿真驗證采用Chan-Taylor聯合算法，用該算法對目標點進行一次定位，將該點作為天牛的初始位置點，以減小天牛在無效區域的探索。

初始值的設定，標志著探索范圍的確定。在定位領域，真正有用的探索區域是目標點附近的區域。對BAS算法的初始值分別采用隨機賦值和經過一次定位賦值2種不同的方式，其他均不變，連續定位多次。然后，采用平均定位誤差作為評判好壞的標準。先對小空間進行考慮，設小空間為50 m×50 m的范圍，其仿真結果如圖8所示。

圖8 小空間對比結果Fig.8 Small space comparison results

同樣，對大空間進行考慮，設大空間為50 000 m×50 000 m的范圍，其仿真結果如圖9所示，各仿真誤差如表1所示。

圖9 大空間對比結果Fig.9 Large space comparison results

表1 初始值與誤差Tab.1 Relationship between the initial value and error 單位：m

對表1中的數據進行分析，因為每一列的隨機誤差相同，但是每一行隨機誤差不同，因此對表1各列進行分析，可以看出在選擇相同的迭代次數的情況下，初始值對于優化算法而言是很重要的，隨機賦值的方式雖然可以增加算法的全局搜索能力，但是在定位方面是無用的，甚至是有害的。在定位范圍較大的空間，采用隨機賦初始值的方式會讓優化算法定位的結果出現較大失誤。

4.1.2 位置更新公式的改進

對位置更新公式進行修改，使每次移動的距離隨著運行的推進而結合實際不斷地變化，可以有效地避免未改進的每次移動均為固定移動距離而與實際不適應的問題，也可以避免采用時變步長造成的探索區域不適應問題。

為了驗證仿真改進后的位置更新公式是否有效，采用2種不同的位置更新公式，對同一個目標點進行定位，最終取定位誤差作為評判標準，其中天牛的初始位置采用一次定位確定，仿真采用50 000 m×50 000 m的空間。仿真定位結果如圖10和圖11所示，定位誤差如表2所示。對于表2，因為每一列的隨機誤差相同，但是每一行隨機誤差不同，因此對表2各列進行分析，可以看出，位置更新公式的改進對于定位準確度同樣有一定程度的提升。

圖10 二維環境下不同的位置更新公式的定位結果Fig.10 Positioning results of different position update formulas in 2D environment

圖11 三維環境下不同的位置更新公式的定位結果Fig.11 Positioning results of different position update formulas in 3D environment

表2 不同的位置更新公式對應的定位誤差Tab.2 Positioning errors corresponding to different position update formulas 單位：m

4.1.3 步長的改進

對BAS算法與Chan算法進行了深入研究發現，步長也是影響BAS算法的主要因素之一，因此對步長進行一定的調整與改進。

神經網絡可以通過訓練來使其擬合度提高，更加適合實際。但是，由于神經網絡的復雜性與定位要求的短時間需求，因此對BAS算法采用訓練的方式，選擇多個步長，提前對一個訓練點進行嘗試性的定位，找到最適合的步長，然后再對目標點進行定位來降低誤差。

首先是二維環境下的仿真，目標點隨機設定，誤差采用高斯白誤差，經過多次仿真發現，經過訓練的BAS算法與Chan算法的融合算法誤差相較于未經過訓練的BAS算法與Chan算法的融合算法有很大程度的降低,仿真結果如圖12所示。在三維環境下的仿真，目標點隨機設定，誤差采用高斯白誤差，經過多次仿真發現，經過訓練的BAS算法與Chan算法的融合算法誤差相較于未經過訓練的BAS算法與Chan算法的融合算法有很大程度減小。其中一次的仿真結果如圖13所示。

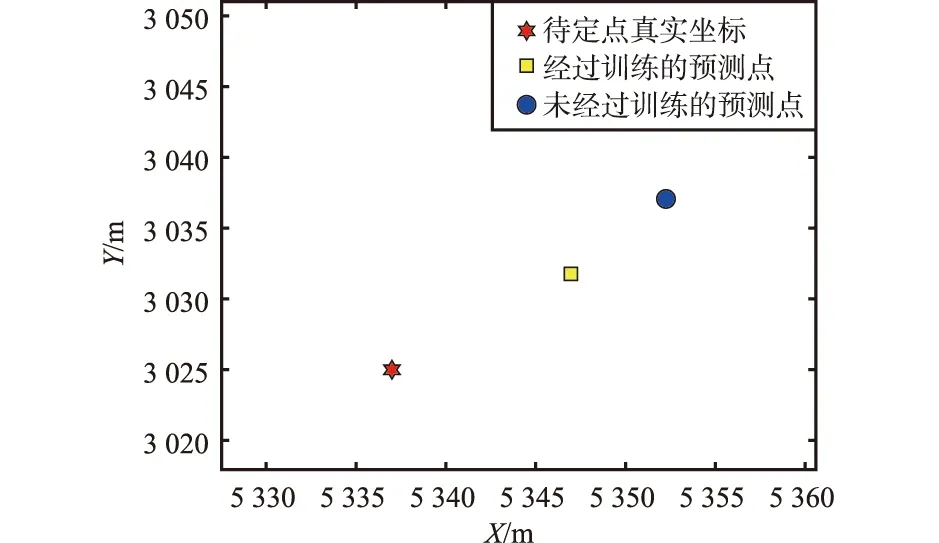
圖12 經過訓練與未經過訓練的天牛須-Chan算法的定位結果對比(二維)Fig.12 Comparison of positioning results of trained and untrained BAS-Chan algorithm(2D)

圖13 經過訓練與未經過訓練的天牛須-Chan算法的定位結果對比(三維)Fig.13 Comparison of positioning results of trained and untrained BAS-Chan algorithm(3D)

未經過訓練與經過訓練的BAS算法的誤差如表3所示。

表3 未經過訓練與經過訓練的BAS算法的誤差Tab.3 Error comparison of untrained and trained BAS algorithm

因為每一列的隨機誤差相同，但是每一行隨機誤差不同，因此對表3各列進行分析，可以看出，步長是影響BAS算法定位精度的重要因素，增加一個訓練部分，以一個訓練點提前確定適合的步長，對于更好地定位有著很大的意義。當步長選擇不合適時，定位會出現相差極大的情況，在相同的采集數據前提下，經過一個訓練，選擇合適的步長，雖然增加了一定的運行時間，但是可以有效地降低最終誤差。

4.2 改進BAS算法與粒子群算法對比

粒子群算法(PSO)是于1987年提出的優化算法，經過多年的發展已廣泛地應用于多個領域，在定位領域也有所應用。對PSO中粒子初始位置同樣也采用一次定位方式進行設置。對于改進BAS算法結合Chan定位和PSO結合Chan定位的對比，分別在二維和三維環境下驗證，二維空間采用50 000 m×50 000 m的空間，三維空間采用50 000 m×50 000 m×50 000 m的空間，目標點采用隨機賦值的方式給定，BAS算法的迭代次數選擇20，PSO的種群數量選擇為50。

二維環境下，目標點隨機給定，粒子群-Chan和天牛須-Chan兩種算法同時對目標點進行定位，誤差采用高斯白誤差。當PSO的迭代次數為200而BAS算法為20時，仿真結果如圖14所示。

圖14 2種優化算法與Chan算法結合后的定位結果對比Fig.14 Comparison of the positioning results of the two optimization algorithms combined with Chan algorithm respectively

當PSO的迭次數與BAS算法的迭代次數相同，均為20時，仿真結果如圖15所示。

圖15 2種優化算法與Chan算法結合后的定位結果對比Fig.15 Comparison of the positioning results of the two optimization algorithms combined with Chan algorithm respectively

在三維環境下對同一隨機目標點進行定位時，當PSO的迭次數與BAS算法的迭代次數相同，均為20時，仿真結果如圖16所示。當PSO的迭代次數增加至200而BAS算法為20時，仿真結果如圖17所示。

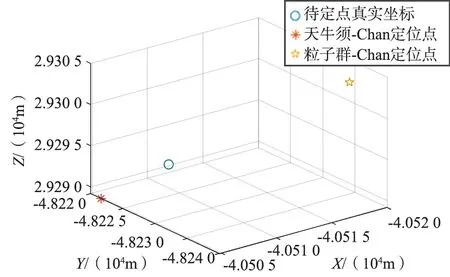
圖16 2種優化算法與Chan算法結合后的定位結果對比Fig.16 Comparison of the positioning results of the two optimization algorithms combined with Chan algorithm respectively

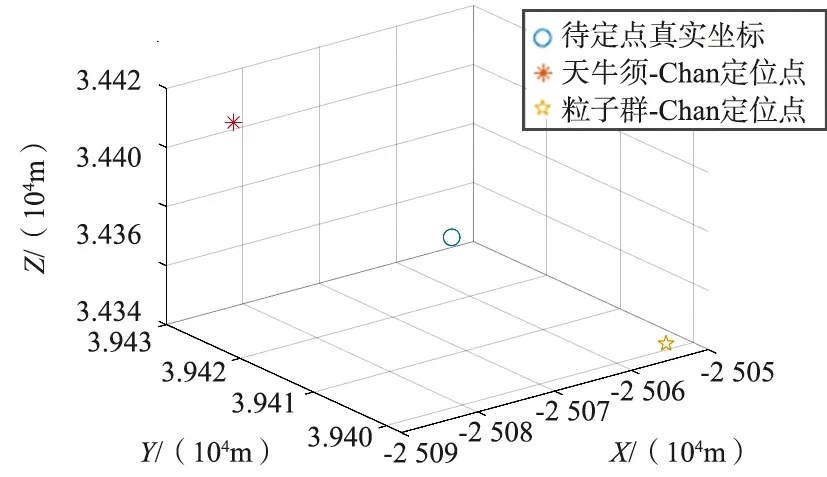
圖17 2種優化算法與Chan算法結合后的定位結果對比Fig.17 Comparison of the positioning results of the two optimization algorithms combined with Chan algorithm respectively

BAS算法與PSO在不同環境下的誤差對比如表4所示。

表4 BAS算法與PSO在不同環境下的誤差對比Tab.4 Error comparison between the BAS algorithm and particle swarm algorithm in different situations

因為每一列的隨機誤差相同，但是每一行隨機誤差不同，因此對表4的各列進行分析，可以看出，雖然BAS算法提出的時間不長，但是BAS算法與Chan定位可以很好地結合，效果比提出多年的PSO與Chan定位的結合算法好。同時，由PSO的定義可以得出，隨著迭代次數的增加，PSO的精度將會上升，但是隨之而來的是運行時間的增加。BAS算法的收斂性很好，在較短的次數內就會收斂，此時即使增加迭代次數，其影響并不會很大，在這個方面，BAS算法更具有優越性。

5 結束語

經過對各個算法改進前后的對比仿真可以看出，經過改進的BAS算法適用于遠距離定位，且精度相較于未改進的BAS算法有很大的提升。經過PSO與改進BAS算法的對比仿真可以發現，改進BAS算法增加的訓練部分可以有效地減小誤差，并且不會對運行時間有較大的影響。同時，相比于PSO，BAS算法僅僅一個天牛，大大降低了運行時間和迭代次數。對于天牛初始位置的確定，一次定位結果的確定，不僅可以使用Chan算法及其優化算法，還可以使用其他定位算法。隨著定位算法的更新以及精確度的加強，定位結果將得到更好的提升。

經過對初始位置、位置更新公式以及步長的改進，BAS算法改善了其不能應用于遠距離定位的問題，且定位精度得到一定的提升，相較于PSO等更有著消耗時間短的優點。

當前，主要是通過事先設定不同數量級的步長，然后通過對訓練點的定位來確定最適合的步長，步長的選擇有一定的局限性，如何在滿足定位時間的需求下選擇合適的步長，以及訓練點的確定方法和天牛的行進策略的改進將是接下來需要完成的工作。