5G MEC系統融合粒子群和教學算法的卸載策略優化

韓松岳，郭基聯

(1.陸軍工程大學 通信士官學校，重慶 400035；2.中國人民解放軍32705部隊，陜西 西安 710086；3.空軍工程大學 航空工程學院，陜西 西安 710038)

0 引言

第五代移動通信技術(5G)采用新型網絡架構，引入虛擬化和軟件定義網絡技術，網絡功能與傳統專用電信設備解耦合，轉而基于通用服務器以軟件包形式運行，實現了虛擬化、模塊化和彈性化部署，從系統架構和網絡功能層面賦予了5G開放、靈活的屬性，使其成為了當前社會各行業信息化、智能化轉型的平臺技術。盡管5G性能參數和能效指標較4G實現了躍升，具有大帶寬、高速率、廣連接和低時延等特點，但是在自動駕駛、遠程手術和虛擬現實等計算密集、時延敏感和數據隔離型應用時，仍需引入移動邊緣計算技術(Mobile Edge Computing，MEC)作為輔助和增強，從而保證服務質量(Quality of Service，QoS)。

5G賦能的智慧教室作為智慧校園的核心應用場景，相較于傳統的數字教室，教學設施和智能終端能夠直接或通過5G CPE間接接入5G網絡，賦能諸如Cloud VR/AR教學、學情大數據分析、課堂監控智能分析和超清遠程直播課堂等新型教學應用。為此，在5G架構下部署MEC系統，任務數據能夠在校園本地完成處理，相較于傳統蜂窩網賦能的云計算智慧教室，節約了傳輸鏈路信道資源，大幅縮短了數據流轉路徑，避免了鏈路擁塞，從而降低業務交付時延和設備能耗，同時，數據不出園區帶來的隔離特性，大幅降低實驗數據、敏感信息和用戶隱私的泄露風險。計算卸載作為MEC的關鍵技術，是指將任務處理過程按相應的卸載策略從移動設備遷移到資源充裕的其他設備上[1]。若缺乏適用于具體場景的卸載策略，系統會根據信道質量、網絡信息和MEC資源可用性，隨機卸載到通信質量好或計算資源充裕的MEC服務器，造成服務器過載，產生額外的時延和能耗，影響用戶體驗質量(Quality of Experience，QoE)。傳統4G與MEC的融合部署，受限于4G架構和物理條件，需在網絡架構中引入控制實體[2]，而5G架構部署MEC由于虛擬網元，因此可選策略更加靈活。

綜上，本文在智慧教室場景下，以5G MEC系統作為信息服務的基礎設施，開展系統構建和優化方法研究具有一定的現實意義。當前，業界學者區分不同卸載場景，針對不同優化目標建模開展了卓有成效的研究。Zhang等[3]提出了一種并行卸載模型和小區域卸載方案，Sun等[4]運用協同PSO解決無人機工業物聯網資源分配問題，Ji等[5]運用強化學習解決了多用戶單MEC場景的卸載優化問題；資源分配研究為所卸載任務分配算力資源[6]。因為卸載策略往往是多目標優化問題，所以上述研究運用到智能優化算法或機器學習算法求解問題，但是上述模型沒有考慮到類似于智慧教室的固定場所場景下MEC系統中終端設備通常由穩定市電供能，不能僅考慮時延優化，還應防止“過載”現象發生，需在模型中加入相應的優化機制。為此，本文主要開展了以下工作：

① 開展基礎理論研究，梳理5G MEC融合機制，結合應用場景構建5G MEC系統架構。

② 依托基金項目開展實驗測試，指出高網絡并發狀態下，VR教學、專網視頻會議和超清直播出現網絡抖動和延遲增大的問題。

③ 基于貪婪思想[7]運用教學算法對粒子群迭代更新后的粒子，進行“教”階段和“學”階段更新，并利用貪婪原則進行迭代，提出融合教學機制的自適應粒子群(Teach & Learn Adaptive Particle Swarm Optimization，TLAPSO)算法，開展仿真實驗，驗證了其收斂性和復雜度的優化。

④ 將所提算法應用到系統模型中，與基于模擬退火算法、粒子群算法和本地卸載的策略進行對比分析，并取得了較優結果。

1 智慧教室信息系統模型構建

1.1 基于多視圖方法論的需求分析

多視圖方法論[8]是指從不同對象的視角對目標系統進行規范化描述，形成相應需求描述視圖用以反映不同對象的訴求，最終形成完善的需求分析框架。

5G智慧教室包含的終端設備數量大、種類多，應用服務具有差異化網絡訴求，網絡服務呈大流量、高并發的特點，在建設與測試階段，面臨計算卸載決策觸發機制可靠性低、卸載位置不合理和資源利用不充分等挑戰。為此，需要研究適用于智慧教室場景的計算卸載策略。本文引入系統工程領域多視圖方法論開展需求分析，形成了如圖1所示的需求分析框架，用以指導后續系統架構設計和模型構建。

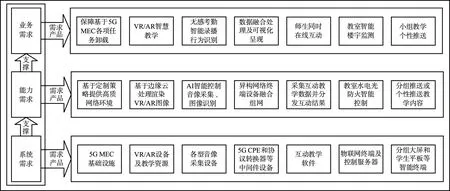
圖1 5G智慧教室需求分析框架Fig.1 Requirement analysis framework of 5G smart classroom

1.2 系統構建和問題描述

以需求為牽引，本文構建了具有遠程互動教學功能的5G智慧教室，系統架構如圖2所示，具體包

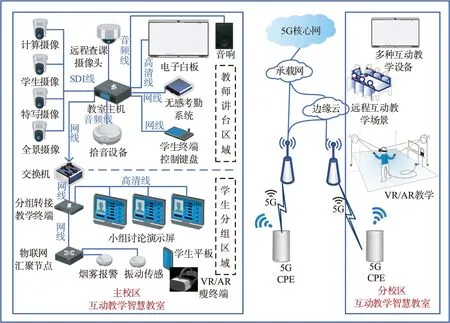
圖2 5G智慧教室抽象模型Fig.2 Abstract model of 5G smart classroom

含現場互動教學、遠程互動教學、VR/AR教學和分組啟發教學4種教學場景。

在實際運用中，智慧教室多場景、多應用交錯運行，有大量網絡需求各異的并行計算業務，因此，易產生較高的時延與能耗，QoS無法得到保證。尤其在VR/AR教學中，基本階段的VR業務網絡端到端時延需小于20 ms，才能確保虛實同步和避免眩暈感，而舒適和理想階段需分別小于15 ms和8 ms時延[9]。然而，智慧教室多建于室內場館，有穩定市電保障，因此，為進一步降低業務的交付時延，合理利用計算資源，本文以能耗約束條件下優化時延為目標，運用TLAPSO算法，基于MEC系統的數學模型對計算卸載進行優化。

算法中，粒子有速度和位置2個向量參數，分別表示粒子移動的方向、步長和潛在可行解，因此粒子編碼的維度與計算任務維度相等，粒子位置向量的元素值表示MEC服務器的編碼，最后通過算法迭代尋優，最終輸出一個代表最優解的位置向量，即為卸載決策向量。

1.3 模型構建與目標確立

根據需求分析框架和智慧教室系統架構，本節就計算卸載過程進行建模，模型中的主要符號含義如表1所示。

表1 主要參數設置Tab.1 Main parameter settings

1.3.1 時延模型

當計算任務量較小時，任務在本地設備處理，產生本地計算時延Tl：

Tl=ci/fu,i，

(1)

式中，ci表示工作負載。fi表示計算密度，即單位數據量所需的CPU周期數，該值與任務類型相關。

當計算任務較大時，則卸載至MEC端處理，計算卸載包含上行傳輸、計算處理和結果反饋3個主要階段，相應地產生傳輸時延、MEC計算時延和反饋時延。在5G架構中，下行鏈路數據傳輸速率快，體驗速率有100 Mb/s，峰值速率達20 Gb/s[10]，且計算結果經過MEC端的編碼壓縮，使得數據量較小，因此反饋時延忽略不計，則計算卸載總時延Ti為：

Ti=Ttrans+Tcal，

(2)

式中，上行傳輸時延Ttrans可由上行傳輸鏈路速率Rij間接求得，根據Shannon-Hartley有：

(3)

Ttrans=ci/Rij。

(4)

而MEC端計算時延Tcal為：

Tcal=ci/fsi。

(5)

1.3.2 能耗模型

任務處理過程主要產生本地計算、上行傳輸和MEC計算處理3種能耗。其中，上行傳輸能耗面向終端設備，由終端發射功率求得：

Etrans=PiTtrans。

(6)

本地計算能耗為：

El=ku(fui)2ci，

(7)

式中，k是由芯片架構決定的能量系數，根據文獻[11]的方法，本文終端設備ku=10-25；fui為終端設備的CPU周期頻率，反映了終端設備的算力水平。

MEC端計算能耗為：

Es=ks(fsi)2ci，

(8)

式中，fsi為MEC服務器的CPU周期頻率，同上述方法，MEC服務器能量系數ks=10-27。

1.3.3 確立優化目標

根據前述分析，智慧教室雖然有穩定的市電保障，但為防止高能耗對供電線路造成高壓負載，避免對設備的生命周期造成損害，應控制卸載在能耗合理范圍約束內。為此，通過增加過載后系統開銷，建立防過載機制。綜合時延與能耗模型，確立優化目標為在能耗約束下，求使得MEC系統時延最小化的卸載決策向量，表述為問題G：

(9)

其中，當任務在本地執行時，式(9)中p=0，并且：

Tl=ci/fu,i。

(10)

當任務卸載至MEC執行時，p=10-2.7并且：

Ti=Ttrans+Tcal，

(11)

s.t.

0≤Pi≤Pimax，

(12)

0≤fui≤fumax，

(13)

0≤fsi≤fsmax。

(14)

在問題G中，式(12)、式(13)和式(14)是面向任務處理全周期的約束條件，即終端發射功率應鉗定在限額內，本地設備和MEC服務器的計算頻率也應在算力的上限范圍內。

2 融合教學機制和粒子群優化的TLAPSO算法

2.1 粒子群算法

PSO的尋優過程通過粒子在搜索空間的飛行完成，粒子每次迭代中的移動由3個部分組成：對上一次速度的繼承、自身學習以及種群的信息交互[12]。其表達式為：

vi(k+1)=ωvi(k)+c1r1[Pbest,i(k)-xi(k)]+

c2r2[Gbest-xi(k)]，

(15)

xi(k+1)=xi(k)+vi(k+1)，

(16)

式中，ω為慣性權重系數；c1，c2表示學習算子，c1表示受自身歷史最優影響程度的大小，c2表示受種群最優影響程度的大小，是控制PSO的迭代最重要參數；xi(k)表示粒子i第k次迭代的位置向量；vi(k)表示其速度向量；r1和r2為隨機因子；Pbest,i為第i個粒子的歷史最優；Gbest為種群最優[13]。

2.2 教與學算法

教與學優化(Teaching-Learning Based Optimization，TLBO)算法由Rao等[14]于2012年提出。相較于其他智能優化算法，TLBO具有收斂速度快、不依賴主觀設置參數等優勢。此后，多人對TLBO算法進行了改進。Li等[15]基于差分進化算法(DE)對TLBO進行了改進，形成混合自適應教學優化算法(ATLDE)，解決了光伏模型未知參數的識別問題。Chen等[16]通過構造自適應框架，將原始TLBO與高斯分布進行融合，新的更新律在搜索過程中以適應度對應的2種模式切換。此外，為了避免初始化過程中的局部收斂，引入了與原始教學和學習階段相關聯的自學習階段。Ma等[17]引入新的種群機制改進了TLBO，提升了收斂速度和精度。李麗榮等[18]引入自適應因子提升TLBO的性能和精度。

TLBO算法主要是模擬以班級為單元的教學方法，班級中學生學習水平的提升需要通過老師的“教”來引導，同時，學員之間需要相互“學習”來提高對知識點的吸收。在該算法機制中，“老師”和“學生”充當了進化算法的種群個體，種群個體中適應度最好的個體充當“老師”身份，每個學員所學的某一科目都對應一種決策變量。具體表述如下：

③ 教學班：將該算法中搜索空間中所有點的集合稱為班。

⑤ 老師：老師并不固定，而是教學班中成績最好的學員，即Xbest，記作Xteacher。

2.2.1 “教”階段

在算法的“教”階段，教學班中每個學員Xj(j=1,2,…,NP)通過計算可以得知個體與班級平均值及教師的差距，并據此差距進行學習追趕。教學方法示意如圖3所示。

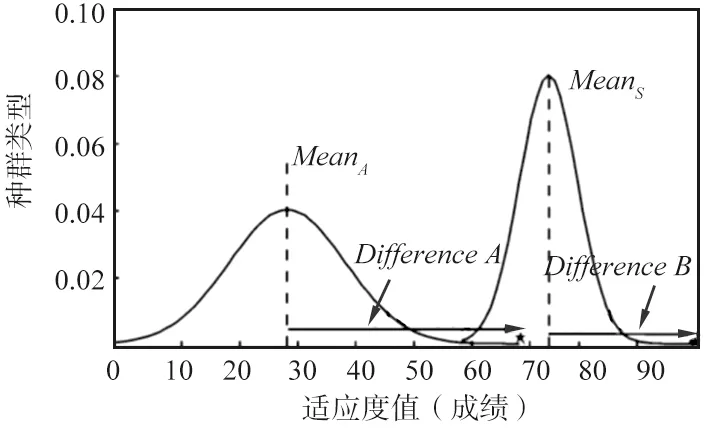
圖3 教學方法示意Fig.3 Schematic representation of teaching methods

由圖3可知，前期的班級平均成績為MeanA=28，成績分布區間跨度較大，通過老師反復教學，后期班級平均成績有所提升，達到了MeanB=74，并且成績分布區間跨度有所壓縮。

在“教”階段，學員通過學習來縮小與老師和學員平均水平之間的差距，該階段可表示為：

(17)

Difference=ri(Xteacher-TFiMean)，

(18)

2.2.2 “學”階段

該階段與鯨魚優化算法(Whale Optimization Algorithm，GWO)的隨機搜索機制類似，通過讓每個學員Xi(i=1,2,…,NP)將隨機一個同學Xj(j=1,2,…,NP,j≠i)視作自己學習競爭的對象，學員Xi與其學習對象Xj進行對比，找到差距所在從而進行學習和追趕，其中，根據學習步長r對每個學員采用不同的學習因子，增加了種群的隨機性，增強了算法擺脫陷入局部最優狀態的能力。學習過程為：

(19)

式中，學習因子ri=U(0,1)表示學習步長。

2.2.3 迭代更新

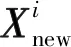
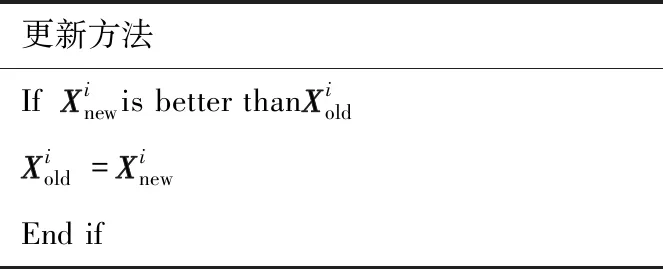
更新方法IfXinewis better thanXioldXiold=XinewEnd if

2.3 算法融合改進

將粒子群更新后的粒子作為教與學算法的學員，利用教與學算法對粒子進行位置更新，TLAPSO算法流程如圖4所示。

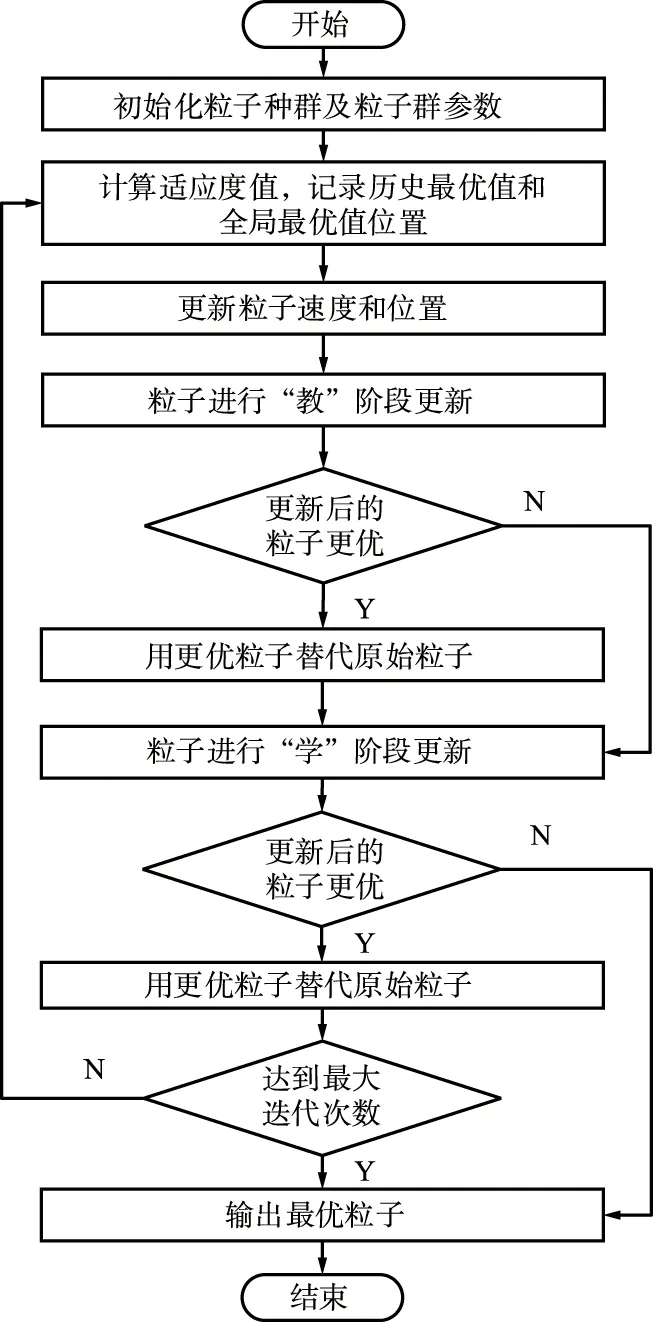
圖4 TLAPSO算法流程Fig.4 Flowchart of TLAPSO algorithm

2.4 算法性能驗證

基于仿真環境Intel Core i5 1.6 GHz處理器，內存16 GB的HUAWEI Matebook14，操作系統Windows10專業版64位，使用Matlab 2018b作為仿真平臺，對融合教與學算法和粒子群算法的改進TLAPSO算法進行驗證分析。

為驗證改進算法的性能，確保算法的通用性和測試條件的完整性，基于單峰、多峰和混合維度多峰3類共23個測試基準函數，對TLAPSO與基本PSO算法開展仿真對比實驗，并針對每個函數連續進行30次實驗，將實驗結果的均值以圖表的形式直觀呈現。表2給出了23個函數的表達式、變量取值范圍、維度和最優值等參數。

表2 測試基準函數表Tab.2 Table of test benchmark functions

續表編號函數維度取值區間fminF21F21(x)=-∑5i=1(X-ai)(X-ai)T+ci[]-14[0,10]-10.153 2F22F22(x)=-∑7i=1(X-ai)(X-ai)T+ci[]-14[0,10]-10.402 8F23F23(x)=-∑10i=1(X-ai)(X-ai)T+ci[]-14[0,10]-10.536 3

將TLAPSO與基本PSO算法在上述測試基準函數上進行比較，設置種群數量為30，最大迭代次數為200，通過連續的30次實驗，2種算法的最優適應度值、最優解對應的平均適應度值、最差適應度值、標準差和算法自用時間如表3所示。

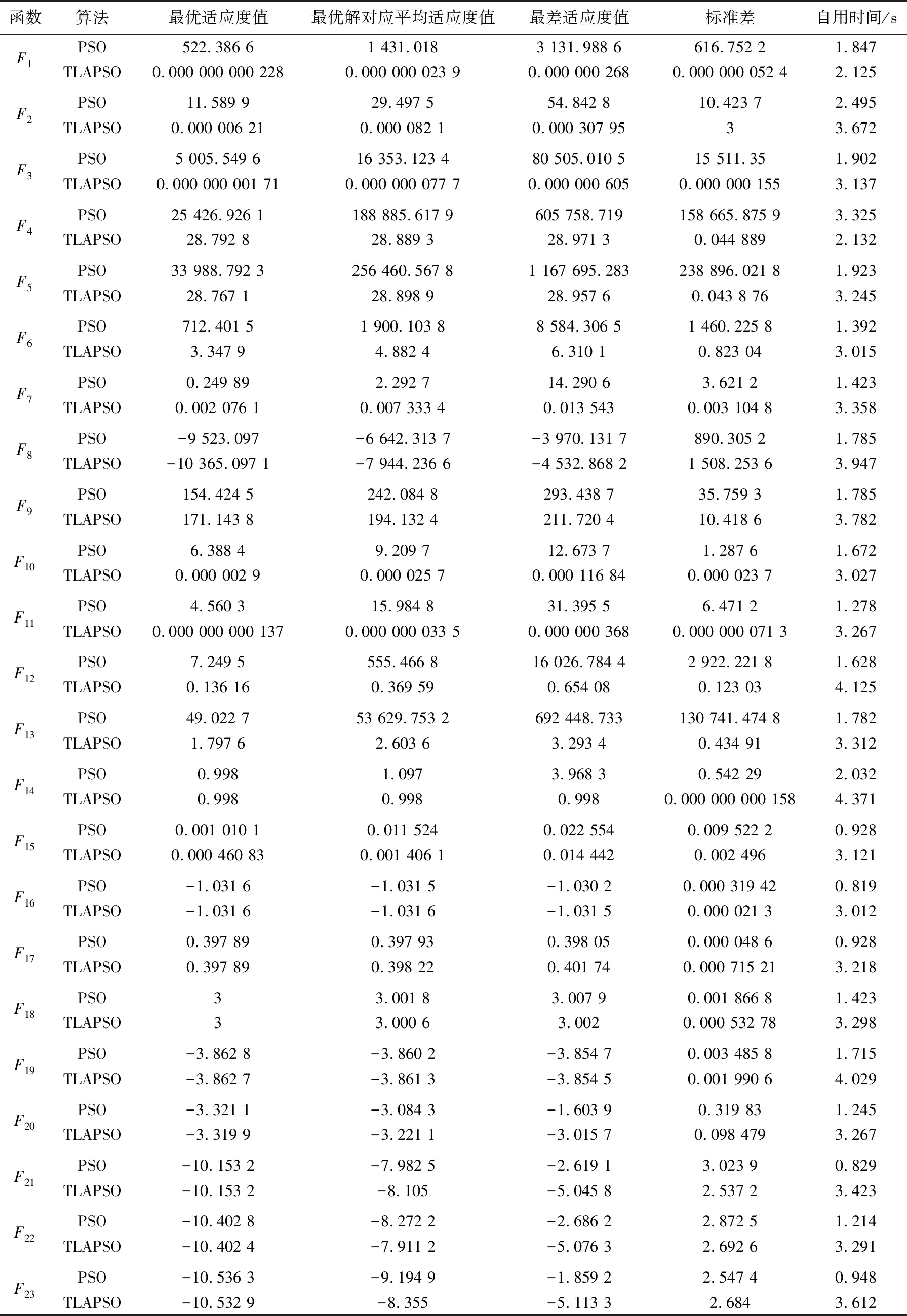
表3 PSO與TLAPSO算法在測試函數上的運算結果Tab.3 Operational results of PSO and TLAPSO algorithms on test functions

實驗結果如圖5和圖6所示，圖5分別是函數F1～F21的實驗結果圖，藍色線條表示原始PSO算法的尋優結果，紅色線條表示TLAPSO算法的尋優結果。從仿真實驗圖像看，在函數F1～F21中，改進TLAPSO算法表現均優于基本PSO算法，具有更快的收斂速度和更優的收斂精度，證明TLAPSO算法性能提升明顯。

但是，圖6中TLAPSO算法在F22和F23函數迭代后期，收斂精度略低于原始PSO算法，但收斂速度仍快于原始PSO算法。其中，在函數F22對比實驗中，2種算法在迭代至第150次時，相互重疊并取得了相同的適應度函數，迭代至166次后，改進TLAPSO算法收斂精度略低于基本PSO算法；函數F23對比實驗中，TLAPSO算法在迭代至131次時，與原始PSO算法出現交叉，并在后面的迭代中，收斂精度略低于原始PSO算法。

客觀上，改進算法通常經過調整參數、融合更新機制或引入其他數學操作，流程上的增加必然導致算法調用和自用時間的增加。但是基于23個測試函數實驗，連續進行30輪，每輪迭代200次算法自用總時間看，改進算法TLAPSO平均自用時間為3.339 s，PSO平均自用時間為1.579 s，復雜度雖較經典PSO有所提升，但收斂性能取得了較大的提升，因此TLAPSO在性能改進的基礎上，算法復雜度得到了較好的控制。

由上述仿真實驗可得,相較于原始PSO算法，TLAPSO算法在解決大部分單峰和多峰函數具有更快的收斂速度和更高的收斂精度，在部分高維問題上，會略微犧牲收斂精度，而取得更快的收斂速度。因此，TLAPSO算法在應對智慧教室中，入網終端設備和MEC服務器數量不大，且裝備設施空間位置相對固定的場景時，能夠取得較好的優化結果。

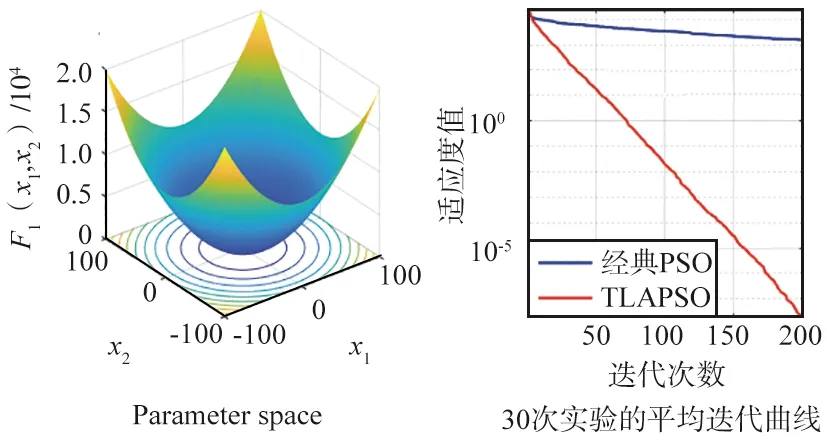
(a) F1

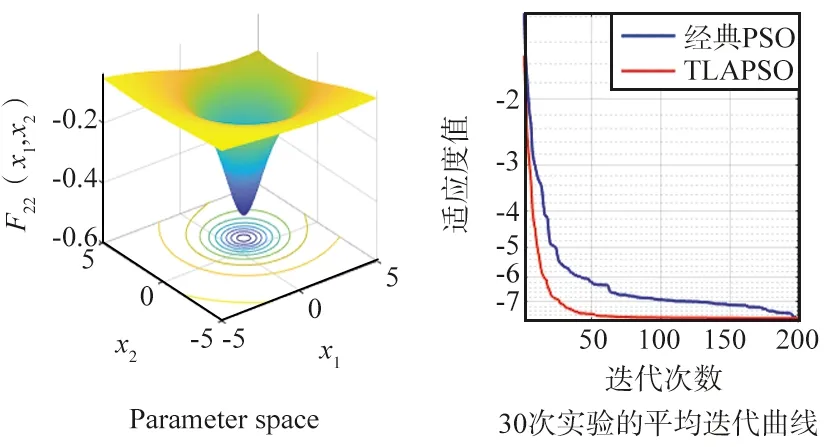
(a) F22

3 基于TLAPSO算法的計算卸載策略優化

3.1 粒子編碼

本文基于整數編碼，令種群數量為M，任務數量為K，MEC服務器的數量為N，用字母T表示計算任務task，則任務集合為T={T1,T2,T3,…,Tk}。其中，每個任務包含3個關鍵信息：處理任務所需的數據量、單位數據量所需的CPU周期和處理該任務的最大能耗約束。因此，用三元數組結構表示Ti(Bi,fi,Emax)，用字母S表示MEC服務器，則MEC服務器集合為S={S1,S2,S3,…,Sn}，用Hij(1≤i≤K,1≤j≤N)表示任務Ti卸載到服務器Sj的上行鏈路信道增益矩陣。

在本文依托的項目背景中，共有3個MEC服務節點為教學場所提供數據卸載分流服務，后期隨著研究與建設的深入，可以對系統進行升級改造，主要節點采用實體MEC系統部署，其余的節點采用軟件虛擬化形式的MEC與4G宏站、5G微站共站部署。假設一個智慧教室中某一時段共有9個大數據量業務需要卸載到MEC端進行處理。則任務集合可表示為T={T1,T2,T3,…,T9}，基于整數編碼的方法，若粒子i編碼為Xi=[1,3,7,0,2,5,4,2,0]，則表示任務T1卸載到編號為1的MEC服務器，任務T2卸載到編號為3的MEC服務器，任務T3卸載到編號為1(7-3-3=1)的MEC服務器，任務T4在本地終端設備執行計算處理。

粒子速度向量用來更新粒子的位置，由式(16)可知，對應于粒子的位置向量，速度向量表示粒子在空間中飛行運動的方向和跨度，其維度與粒子編碼相對應，因此，每個維度的元素值表示任務卸載服務器編碼位次的變化。

3.2 適應度函數

本文以智慧校園為背景，針對智慧教室作為應用場景進行建模，從前述分析可知，智慧教室有穩定的市電保障，因此，為降低模型和算法復雜度，進一步提升卸載效率，將模型簡化為在能耗約束下最小化時延，并且當卸載任務產生的計算能耗大于能耗約束時，會增加卸載代價。因此，算法的適應度函數為：

(20)

3.3 基于TLAPSO算法的計算卸載流程

受教學活動啟發，將“教與學”算法與粒子群算法相融合，通過收斂速度更快、尋優精度更高的TLAPSO算法解決計算卸載問題，結合圖4所示的算法流程，步驟如下：

(1) 初始化

初始化種群及相關參數。賦予粒子隨機位置和速度向量，設定種群規模M=30，MEC服務器數量N=5，加速常數c1=c2=1.5，慣性權重ω=0.8，為確保粒子不飛出邊界而錯過最優解，設定最大速度vmax=10，最大位置邊界xmax=5，最大迭代次數設為150。

(2) 計算適應度值，記錄歷史和全局最優

基于給定的參數計算總時延和能耗，得出每個粒子適應度值。其中，歷史最優值為從初始迭代到當前粒子所遍歷的最好位置，可記為Pbest,i；所有迭代中的適應度值最優的粒子為種群最優值，記為Gbest。

(3) 粒子迭代更新

當迭代次數小于80時，則循環進行粒子“教”階段和“學”階段的迭代更新:

“教”階段的位置更新為：

(21)

“學”階段位置更新為：

(22)

速度更新時，當粒子速度超出速度最大限制，則用該速度作為最大速度邊界值更新粒子速度。

(4) 用更優粒子替代原粒子

通過前面設定的參數值，計算粒子的適應度值，并遴選更優的粒子替代Pbest,i和Gbest。

(5) 停止準則處理

當達到最大迭代次數時，則停止更新，此時輸出的卸載決策向量Vi即為所求的全局最優解，且適應度函數值為時延最小開銷。在迭代中，若更新的粒子適應度值趨于平穩，不再有上下波動變化，則確定已找到全局最優解，停止更新并輸出結果。

3.4 TLAPSO算法在MEC系統中的實現與應用

通過算法的迭代和尋優，在特定場景及其參數下，能夠快速得出全局最優的卸載策略。可以通過在系統中引入控制實體，將基于TLAPSO算法的卸載調度策略寫入調度模塊，實現卸載策略的應用，也可以將基于優化算法的卸載策略通過API接口寫入MEC系統層的編排器中，實現基于特定策略的計算卸載。

4 仿真實驗及對比分析

4.1 環境搭建及參數設置

基于與3.4節中相同的平臺環境進行仿真。為進一步量化評估部署MEC系統后，業務時延的改善與優化，對比應用不同卸載策略的效果，遴選出適用于智慧教室場景的卸載策略。根據前述模型和問題G，對基于本地卸載執行(未部署MEC系統)、TLAPSO算法、基本PSO算法和SA算法的卸載策略進行仿真實驗，對比分析上述4種卸載策略的性能，給出部署MEC系統對5G智慧教室網絡承載優化程度的定性評價，以及采用不同卸載策略對5G MEC系統優化改善的定量評估。仿真實驗參數設置如表4所示。

表4 主要參數設置Tab.4 Main parameter settings

4.2 仿真實驗設計

4.2.1 任務量實驗

本實驗以終端設備的任務量為變量，以MEC系統在能耗約束下的卸載總時延作為系統總開銷，衡量不同卸載策略在相同參數環境下的收斂性能。設置相關參數如下：MEC服務器數量S=8，終端設備產生的任務數一共有T=60個，任務量分別設置為[5，10,15,20,25,30,35,40,45,50] MB，仿真結果如圖7所示。

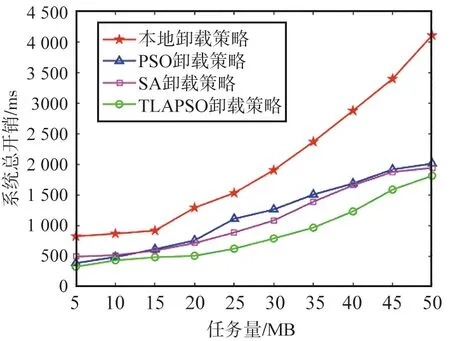
圖7 任務量實驗結果Fig.7 Experiment results of task volume

從仿真結果看，本地卸載策略在實驗初始階段任務量較小的情況下，相較于將計算任務卸載到MEC服務器，有較大的卸載開銷。同時，隨著任務量的增加，本地卸載策略的系統總開銷增幅最大，足以證明在智慧教室部署MEC系統能夠有效地降低業務交付時延，提升用戶體驗。此外，基于SA算法的卸載策略在實驗任務量較小的初始階段，系統總開銷略高于基于PSO算法的卸載策略，經過分析推論為在處理低維度問題時，復雜度較高的SA算法給系統造成了額外的時延，但在任務量適中的場景下，優化效果好于PSO算法，在任務量較大的場景下，優化效果與PSO接近。基于TLAPSO算法的卸載策略在任務量較小時優化效果并不明顯，但隨著任務量的增加，優化效果遠優于其他卸載策略，即TLAPSO卸載策略在大任務量場景中的優化效果更加明顯。

在該實驗中，TLAPSO卸載策略對系統的優化程度最大值在任務量為50 MB時，較本地卸載策略優化提升了55.90%。

4.2.2 能耗容忍度實驗

雖然智慧教室有穩定的市電供能，但是隨著智慧校園形態的發展演進，未來將融入更多的物聯網和移動互聯網終端設備，并且智慧化教學手段不再局限于教室，而是向室內外聯動教學和異地智慧化教學演進[19]。因此，在室外條件下的供能與能耗，將直接影響到室外教學條件的構設、供能方式的優選和終端設備的壽命周期。

為了拓展TLAPSO卸載策略的適用場景，本實驗通過控制設備產生的任務數量、MEC服務器數量和任務量大小3個變量，增加能耗容忍條件限度，觀察不同卸載策略的表現。設定參數如下：MEC服務器數量S=8，終端設備產生的任務數一共有T=60個，任務量大小為5 MB，仿真結果如圖8所示。

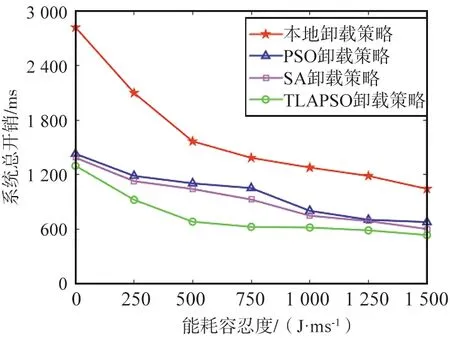
圖8 能耗容忍度實驗結果Fig.8 Experimental results of energy consumption tolerance

從仿真結果看，隨著能耗容忍度的增加，系統總開銷呈遞減趨勢。其中，本地卸載策略卸載總開銷遠高于其他卸載策略，并且前期能耗容忍度不高時，開銷減小速度快于后期，因為終端設備的CPU算力有限，超過其上限后，即使再增加能耗容忍，終端設備的敏感度也會降低，同樣說明了將任務卸載到MEC服務器處理的必要性。此外，SA卸載策略與PSO卸載策略優化效果接近，TLAPSO策略優于其他卸載策略。

在該實驗中，TLAPSO卸載策略對系統的優化程度最大值在能耗容忍為0 J·ms-1時，優化率達54.02%。

4.2.3 MEC服務器數量實驗

該實驗以待處理的任務總量為變量，分別設置5臺和10臺MEC服務器，都以TLAPSO卸載策略進行仿真實驗。設置參數如下：任務總量分別設置為[300,600,900,1 200,1 500,1 800,2 100,2 400,2 700,3 000] MB，仿真結果如圖9所示。

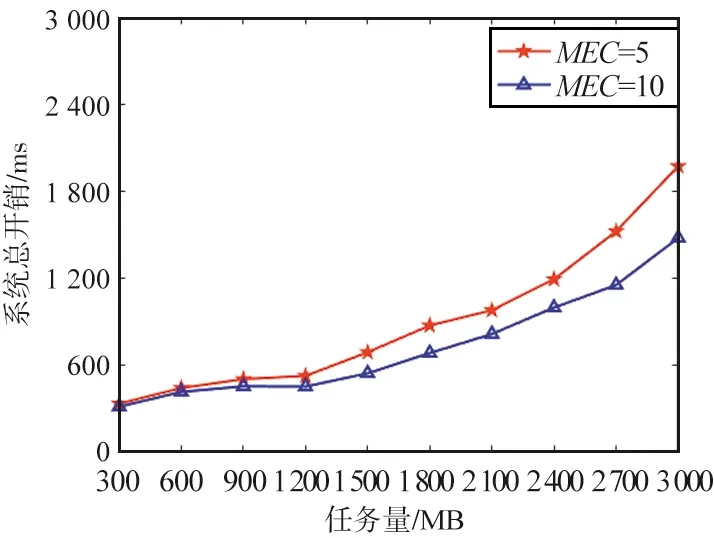
圖9 MEC服務器數量實驗結果Fig.9 Experimental results of the number of MEC servers

從仿真結果看，隨著待處理任務總量的增多，藍色折線上升趨勢變緩，并且系統總開銷始終低于紅色折線，說明MEC數量增多，不僅MEC端整體算力有所增強，同時粒子尋優的可行解維度也有所增加，計算任務根據距離、MEC服務器算力性能和信道質量等因素，可選的服務器更多。此外，本文中的模型設置了防過載機制，能夠有效防止計算任務過多卸載至通信和計算資源條件更優的服務器上，杜絕因過載而產生額外的能耗和時延。

4.3 結論分析

從上述4種卸載策略的仿真實驗結果看，在5G網絡架構中部署MEC系統，能夠有效降低系統總開銷，優化智慧教室場景中的業務交付時延，提升QoE。同時，基于TLAPSO算法的卸載策略相較于本地卸載、PSO和SA卸載策略具有更高的卸載效率，能夠更好地提升系統效能。

在智慧校園的發展演進中，隨著入網設備的增多，海量數據的本地云化處理需求相應地提升，應當以現有網絡基礎設施為依托，以教學科研和校園治理業務需求為牽引，基于校園布局、路測數據和網優規劃手段，增加MEC節點數量，但是由于當前5G MEC實體服務器成本高昂，可以考慮以少量實體服務器為中心，分布式部署虛擬化MEC節點，實現過渡階段的平滑演進，滿足智慧校園個性化業務的差異化網絡需求。

5 結束語

以5G智慧教室為應用場景，對計算卸載的優化問題進行了研究。首先，歸納了5G與MEC的融合部署方式、分流機制和卸載決策，梳理了近年來實用的群智能優化算法，基于多視圖方法論開展了需求分析。其次，構建了基于5G MEC技術的智慧教室系統架構，并對優化目標進行了建模，結合課堂教學過程的啟發，提出了TLAPSO算法，通過仿真實驗，證明了改進算法性能的提升。最后，基于實驗數據，對比分析了多種卸載策略的效果，從定性和定量兩方面驗證了智慧校園中部署MEC系統的必要性，以及TLAPSO卸載策略的優越性。

今后將針對MEC集群化部署、卸載策略的前端實現和基于深度學習的優化策略開展研究，以實體或軟件包的形式實現算法優化套件，提升系統簡潔運維、優化策略快速上線和MEC系統的綜合效能。