方程與不等式思想在“數與代數”問題中的應用
——以2021年中考題為例

周澤軍

(湖北省武漢市光谷實驗中學,430223)

本文從概念、性質、圖形或圖象、實際應用四個方面探究方程與不等式思想在中考中的應用.

一、由概念產生方程與不等式

例1(2021年聊城中考題)關于x的方程x2+4kx+2k2=4的一個解是-2,則k的值為( )

(A)2或4 (B)0或4

(C)-2或0 (D)-2或2

解析此題考查了方程的解的概念.

把x=-2代入方程x2+4kx+2k2=4,得4-8k+2k2=4,解得k1=0,k2=4.故選B.

解析此題考查了二元一次方程(組)解的概念.

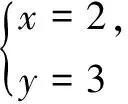
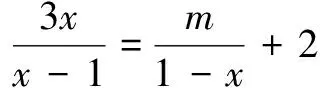
解析此題考查了解分式方程和解一元一次不等式.

將原分式方程去分母,得3x=-m+2(x-1),去括號、移項、合并同類項,得x=-m-2.由方程的解為正數,可得-m-2>0且-m-2≠1，解得m<-2且m≠-3.

評析本題的解題思路分為三步:一是求解關于x的分式方程,二是由題意得到關于m的不等式并解之,三是注意隱含條件(分式的分母不為零)對參數取值的限制.

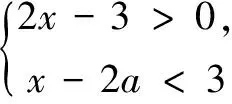
解析此題考查了解一元一次不等式組.

由題意，可得3<2a+3≤4,

評析對于含字母系數的不等式(組),先把其中的字母看作已知數,求出其解集(即用含字母的代數式表示解集),再依題對解集的具體限制,得到新的方程(組)或不等式(組),最后由新的方程(組)或不等式(組)解決問題.

二、由“性質”產生方程與不等式

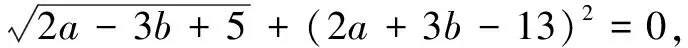
(A)8 (B)6或8

(C)7 (D)7或8

解析此題考查等腰三角形的性質、三角形的三邊關系、二元一次方程組等知識點,以及分類討論思想.

由非負性,得到方程組

∴等腰三角形的周長為7或8,故選D.

例6(2021年廣元中考題改編)將二次函數y=-x2+2x+3的圖象在x軸上方的部分沿x軸翻折后,所得新函數的圖象如圖1所示.

(1)過點(4,0)的直線與新函數的圖象只有1個公共點時,則直線的解析式是______.

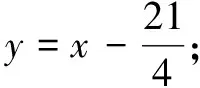
(3)當直線y=x+b與新函數的圖象恰有4個公共點時,則b的取值范圍是______.

解析易得拋物線y=-x2+2x+3與x軸的交點為A(-1,0),B(3,0),翻折部分的拋物線解析式為y=(x-1)2-4(-1≤x≤3).

(1)分兩種情況討論:

當直線平行于y軸時,x=4.

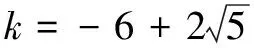
(2)分三種情況討論:

當直線與x軸平行且過(1,-4)時滿足條件,此時y=-4.

根據題意,可設滿足條件的直線解析式為y=x+b.

當直線y=x+b過點B(3,0)時,直線與新函數圖象恰好有三個公共點.

此時,3+b=0,解得b=-3.

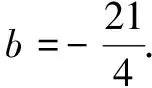
評析例6是利用一元二次方程根的判別式的性質解決問題.

三、由圖形或圖象產生方程與不等式

例7(2021年日照中考題)如圖3,在矩形ABCD中,AB=8cm,AD=12cm,點P從點B出發,以2cm/s的速度沿BC邊向點C運動,到達點C停止.同時,點Q從點C出發,以vcm/s的速度沿CD邊向點D運動,到達點D停止,規定其中一個動點停止運動時,另一個動點也隨之停止運動.當v為______時,?ABP與?PCQ全等.

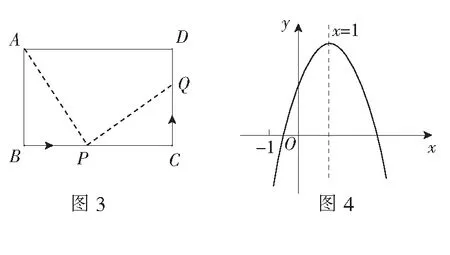
例8(2021年遂寧中考題)已知二次函數y=ax2+bx+c(a≠0)的圖象如圖4所示,有下列5個結論:①abc>0;②b2<4ac;③ 2c<3b;④a+2b>m(am+b)(m≠1);⑤ 若方程|ax2+bx+c|=1有四個根,則這四個根的和為2.其中正確的結論有( )

(A)2個 (B)3個 (C)4個 (D)5個

評析從知識的融合處設置問題,既可以考查學生思維的深度與廣度,還可以有效地考查學生運用數學知識和思想方法解決問題的素養與能力.如,例7是方程思想在幾何中的應用,例8是方程思想在函數中的應用.其中二次函數的圖象與系數關系類問題主要考查圖象的形狀、大小、位置,函數解析式中系數變化與圖象大小、圖象位置的關系,函數的增減性、最值、圖象對稱性、函數值的大小比較等.

四、實際應用中產生的方程與不等式

例9“十一”期間,小明一家乘坐高鐵前往某市旅游,計劃第二天租用新能源汽車自駕出游.

根據圖6提供的信息,解答下列問題:

(1)設租車時間為x小時,租用甲公司的車每日所需費用為y1元,租用乙公司的車每日所需費用為y2元,分別求出y1,y2關于x的函數表達式;

(2)當租車時間為多少小時時,兩種方案所需費用相同;

(3)根據(2)的計算結果,結合圖象,請你幫助小明分析選擇怎樣的出游方案更合算.

例10(2021年臺灣中考題)碳足跡標簽是一種碳排放量的標示方式,讓大眾了解某一產品或服務所產生的碳排放量多寡,如圖7所示.碳足跡標簽的數據標示有其規定,以碳排放量大于20公克且不超過40公克為例,此范圍內的碳足跡數據標示只有20,22,24,…,38,40公克等11個偶數;碳足跡數據標示決定于碳排放量與這11個偶數之中的哪一個差距最小,兩者對應標示的范例見表1.

表1

請根據上述資訊,回答下列問題,并詳細解釋或完整寫出你的解題過程.

(1)若有一個產品的碳足跡數據標示為38公克,則它可能的碳排放量之最小值與最大值分別為多少公克?

(2)承(1),當此產品的碳排放量減少為原本的90%時,請求出此產品碳足跡數據標示的所有可能情形.

解析此題是一道開放性題,考查了不等式的相關知識.將現實生活中的情境與數學思想聯系起來,需要理解題目所給的信息,并分析出各個數量之間的關系.第(1)問根據題干中關鍵語句“碳足跡數據標示決定于碳排放量與這11個偶數之中的哪一個差距最小”,可得碳排放量之最小值與最大值分別為37.0公克和39.0公克.第(2)問由第(1)問的最大值和最小值乘以90%,分別得到33.3公克和35.1公克,進而求出此產品碳足跡數據標示的所有可能情形為:34,36.

評析上述試題均是以實際問題為情境,注重培養與滲透學生的生活情境數學化能力.解答此類問題的關鍵是仔細分析題目的文字信息,從問題情境中抽象出數學問題,并建立數學模型.