基于PBL模式的初中數學教學思考
——“二次函數”第一課時課堂實錄與思考

?蘇州高新區實驗初級中學 蔡春艷

1 引言

PBL模式是一種以問題為導向的教學方法(problem-based learning，PBL)，由美國的神經病學教授 Barrows 首創.它遵循以學生為中心，強調學生的主動學習，發揮學生的主體性，使學習者投入于問題中，通過學習者的自主探索和合作交流來解決問題，從而學習到問題中隱含的知識，并在此過程中發展解決問題的能力和自主學習的能力[1].

筆者最近參與了一節蘇州市評優課“二次函數”的磨課過程.“二次函數”是初中數學的核心內容，這一章的邏輯結構與一次函數相似，是對函數知識的完善和提高.第一課時的重點為理解概念，如果按照傳統模式，理解概念—應用概念，學生會缺乏學習課程的新鮮感，也無法從整體上理解二次函數.課程標準提出，“學生的學習應當是一個主動的過程.教學活動應引導學生在真實情境中發現和提出問題，分析和解決問題”[2].PBL理念與課程標準一致，因此筆者嘗試采取PBL理念，即基于問題展開學生的學習，對教學過程作出梳理，供研討.

2 課堂實錄

2.1 環節(一)——創設情境，引入新課

師：同學們好，我來自蘇州新區實驗初中，昨天開車來到我們常熟外國語學校.

如圖1，在這段運動過程中涉及哪幾個量？

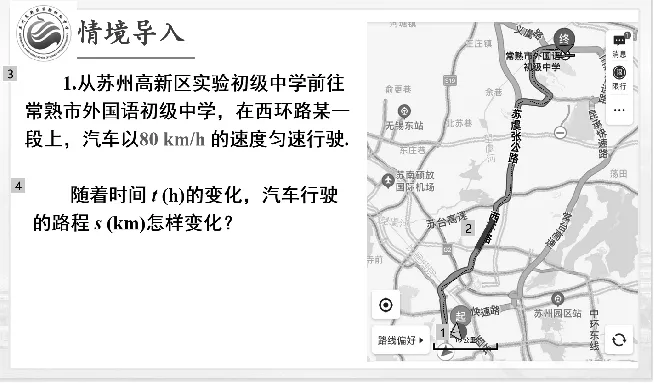
圖1

生:時間、路程、速度.

師：這里的速度是常量，路程S和時間t是變量.這兩個變量之間是什么關系？

生：S=80t.

師：S是t的函數嗎？為什么？

生：是的.因為在這個變化過程中有兩個變量S和t，對于t的每一個值，S都有唯一的值與它對應.

師：這是什么函數？

生：正比例函數.

師：正比例函數也是什么函數？

生：一次函數.

師：如圖2，在這個過程中，t與v又有怎樣的關系？是我們學過的函數嗎？

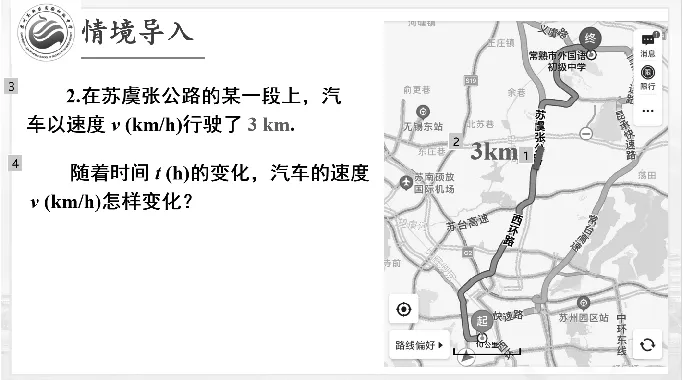
圖2

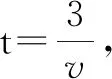
師：有一段下坡路，若不踩油門，隨著時間的變化，汽車的速度會怎樣變化？(學生沉默了半分鐘.)

師：大家可以回想一下自己騎自行車下坡的體驗，你感覺速度怎樣變化？

生：速度越來越快.

師：可見，這不再是一個勻速運動.此時，路程與時間會是怎樣的關系呢？為了探究這個問題，我們來做一個實驗.

數學實驗：播放小車沿斜面下滑的視頻.

通過數學實驗得到數據，如表1.

表1 實驗數據

師：觀察表1，你認為S是t的函數嗎？是一次函數嗎？是反比例函數嗎？

生：S是t的函數，但既不是一次函數，也不是反比例函數.

師：請同學們畫出這個函數的圖象.(投影展示)

師：老師和大家一樣也畫出了圖象，請看圖3，這是我們熟悉的函數圖象嗎？

圖3

生：不是.

師：這是一個新的函數.我們通常是怎樣研究函數的？

生：研究函數的概念、圖象、性質,運用函數知識解決實際問題……

師：概念通常又是怎么得到的？

生：從生活中實際問題抽象而來.

師：是的，生活中存在很多類似的函數關系……

設計意圖：上課開始，教師就和學生分享了從自己學校到學生所在學校的路上的歷程，拉近教師與學生的距離，將學生從數學課堂帶入現實生活情境中，符合PBL模式中設計完整學習情境的理念.在這個情境中，學生體會到可以用數學語言來解釋現實世界中的現象，發現在不同情境下，路程與時間、速度與時間的函數關系.通過已經學過的函數關系，回顧研究函數的一般思路，為本節課進一步研究新的函數奠定基礎. 研究下坡路時路程與時間的函數關系，就是建模的過程，通過實驗，由形入手，發現了一類新的函數.這是什么函數，它有什么特征，有什么作用？在問題的驅動下開始本章節的研究.

2.2 環節(二)——自主探究，合作交流

校園風景如畫，老師帶領同學們來到學校門口的水池旁，一起觀察.

(1)水滴激起的波紋不斷向外擴展，圓的面積 S 與半徑 r 之間的函數關系為.

(2)學校在另一側再建一個周長為20m的矩形水池，水池的面積S(單位：m2)與一邊長 x(單位：m)之間的函數關系為.

(3) 如圖4，外側矩形長10m，寬3m，水池的邊緣是等寬的，寬度為 xm，則中間小矩形的面積 y(單位：m2)與 x之間的函數關系為.

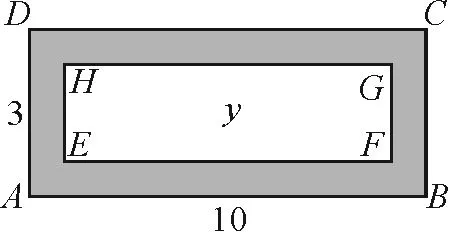
圖4

問題1S=πr2，S=-x2+10x，y=4x2-26x+30三個表達式有什么共同特征？

歸納得到二次函數的概念：一般地，形如y=ax2+bx+c(a，b，c是常數，且a≠0)的函數叫做二次函數.其中x是自變量，y是x的函數.

學生討論概括二次函數解析式的特征：(1)等號右邊是關于自變量的整式；(2)最高次項的次數是2；(3)二次項系數不等于零.

問題2在以上實際問題中，自變量可以取哪些值？

歸納得到二次函數自變量的取值范圍：

(1)通常二次函數y=ax2+bx+c(a≠0)的自變量x可以是任意實數.

(2)如果二次函數的自變量表示實際問題中的某個變量，那么它的取值范圍受到實際意義的限制.

設計意圖：在PBL模式的理念下，學生需要在一個真實的情境中對驅動問題展開探究.環節 (一)中，學生已經明確了要研究的問題，并對這個問題產生了濃厚的興趣.環節(二)中，教師帶領學生進入真實的校園場景，觀察校門口的水池，探究水滴入水、水池面積等變化過程中變量之間的關系，發現這些變量之間的共同特征，從而歸納出新的函數——二次函數，并在此基礎上展開研究.

2.3 環節(三)——動手操作，解決問題

小組活動：每人寫一個二次函數，請同桌說出二次項系數、一次項系數和常數項.

例題如圖5，學校在長300m，寬90m的矩形廣場內修建等寬的十字形道路，設道路寬為 xm，綠地面積為ym2. 你能寫出綠地面積與道路寬之間的函數表達式嗎？道路寬的取值范圍是什么？

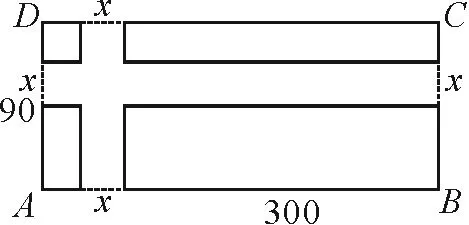
圖5

探究如圖6，用長50m的護欄圍成一塊靠墻的矩形花園，墻的長度是20m.請利用本節課所學知識，提出一個問題并解決，分小組完成.

圖6

設計意圖：學生通過環節(二)的探究得到一個“產品”(PBL模式的特征之一)——二次函數模型，環節(三)繼續帶領學生漫步校園，從教學樓前的花壇入手，學生以小組合作的形式，提出問題并解決問題，體現了PBL模式的項目式教學.在解決問題的過程中，學生可能需要用一元二次方程或二次函數的性質來解決問題，也可能需要思考方程、不等式與二次函數的關系，學生在思考、探索等過程中得到了必要的數學思維訓練，體會到了數學思維的多元性，并且激發出后續研究二次函數性質的好奇心與求知欲.

3 基于PBL模式的課例賞析

3.1 基于問題情境展開學習

環節(一)為教師到學校路途中所遇之景，環節(二)為進校所見一景，環節(三)為教學樓前一角景觀，整節課基于漫步校園所遇之景的變化，由學生自己提出問題，主動探索問題，圍繞二次函數的概念這一主線展開學習.學生的學習體現了PBL模式的兩個要點：

(1)學生是學習的主人

在PBL模式中，學生是學習的主人. 在本課的學習中，不再由教師講授知識，而是學生自主探索.如環節(一)，每個學生都可以根據自己的生活經驗和學習狀態多角度思考，從而得出不同程度的結論，學習積極性被調動起來了.環節(二)，圍繞校園里的水池，學生觀察水滴入水的過程，思考擴建水池的設計，發現這些過程中變量的關系，提煉它們的共同特征，從而歸納得出一類新的函數——二次函數.

(2)在問題解決過程中獲得新知識，發展新能力

環節(一)，下坡路段上路程隨時間變化的關系，學生由生活經驗可知是函數但不是一次函數，問題有一定的難度，學生一時無法解決.通過數學實驗，得出路程隨時間變化的數據，再畫出函數的圖象，既可以讓學生感受到函數的不同表現形式，感受數形結合，也充分發揮了學生的主體作用.環節(二)和環節(三)，學生在探究過程中，不僅學習了二次函數這個新的知識，而且親自參與建模過程，這些都體現了PBL模式的“在探究過程中學習及應用學科思想”.

3.2 基于問題的教學反思

教師的教學圍繞PBL模式的三個要點展開：

(1)以激發求知欲和好奇心為支點

教育心理學的研究指出,好奇心是推動兒童和成人去獲得新知識的主要動機.學生的求知欲和好奇心是課堂活力的源泉，是課堂教學價值的支點.如何激發學生的求知欲和好奇心呢？本課從學生熟悉的騎車上坡下坡問題入手，結合校園里的真實場景，讓每個學生都有話可說，有法可想，培養了學生的發散思維.學生獲得了成功的體驗，學習積極性也被調動起來了.

(2)教師是輔助者和引導者

環節(三)原先的設計是由教師呈現一組題，學生練習，以題目增強二次函數的概念的鞏固.但是PBL模式中，教師是指導學生認知學習技巧的教練，因此最終繼續創設情境，放手讓學生自主探索.再如環節(二)，教師在學生歸納得出二次函數概念的基礎上，結合實際問題，考慮自變量的取值范圍，有利于培養學生思維的嚴謹性，體現了教師引導者的角色.

(3)真實的基于績效的評價

課程標準提出，學習評價的主要目的是為了全面了解學生數學學習的過程和結果，評價要關注學生學習的結果，也要關注學習的過程.PBL模式中要求建立真實的基于績效的評價.環節(一)，遇到新函數教師沒有避開不談或者直接告知，而是通過數學實驗，讓學生親自經歷探索兩個變量關系的過程，環節(三)，互相提問，既利于調動學生學習積極性，也可以暴露學生思維的局限性，最后在教師的引導下共同歸納注意要點.

4 結論

PBL在國外已形成一套成熟的教學方法，學生通過規劃和完成一系列任務，最終實現某個目標或者解決某個問題，這就是項目.學生為了成功地完成項目，必須整合自己的學科知識和生活經驗，促進團隊協作，最終對自己或他人的表現作出評價，這是PBL教學法的精髓[3].在國內，由于課程時間的限制，不能很好地實行項目教學，比如，本課的驅動問題還需后續研究二次函數的圖象和性質才能解決，無法在一節課內完整體現.再如，數學實驗部分，按照PBL理念應該讓學生真正進入數學實驗室，借助打點計時器，記錄路程隨時間變化的數據，再通過數據畫出函數的圖象，這樣可以更真實地經歷從實際問題中抽象函數模型的過程，感受研究函數的方法，但是時間所限，本節課老師采用課前做實驗，錄好視頻在課堂上播放的方式，也是一種變通與嘗試.