轉化策略在解題中的應用
?甘肅省天水市秦州區藉河南路天水石馬坪中學 王文錫
1 一般與特殊的轉化
一般與特殊相互之間的轉化,主要是指通過一般規律求個例特殊問題以及列舉特殊例子對一般性問題進行解答[1].如特殊圖形求解,可通過填補或分割將其轉化為常見的一般圖形,進而根據公式解答.掌握這種轉化策略,有助于提升解題的效率.
例1已知半圓的直徑AB=12 cm,點C,D是這個半圓的三等分點,求弦AC,AD和弧CD圍成的陰影部分面積.(結果用π表示.)
分析:如圖1,因為陰影部分對應的是不規則圖形,因此無法直接求解其面積.題目中提到了三等分點,連接OC,OD,因為點C,D是這個半圓的三等分點,故弧AC,CD,DB均為60°.
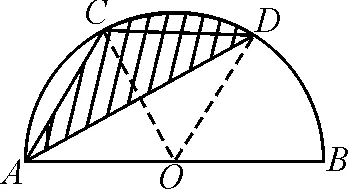
圖1
解:∵∠ADC=∠DAB,
∴AB∥CD.
∴S△ACD=S△OCD.
又∵∠COD=60°,
2 數形轉化
數形轉化求解問題較為常見,是指把具體的代數問題轉化為圖形問題進而解答,或將圖形等價轉變為具體的代數問題求解.這種轉化求解思路可以體現在數軸、函數圖象、幾何圖形等不同方面,需要重點學習和關注.
例2若a+b<0,a<0,b>0,試判斷a,-a,b,-b的大小關系.
分析:與大小關系有關的問題,往往可以借助數軸這一幾何圖形就能夠直觀地把字母a,-a,b,-b表示出來.
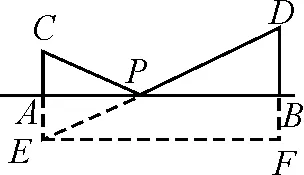
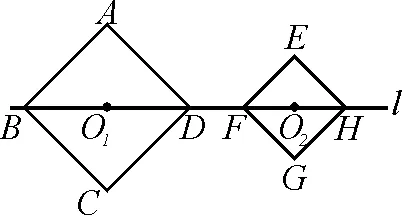
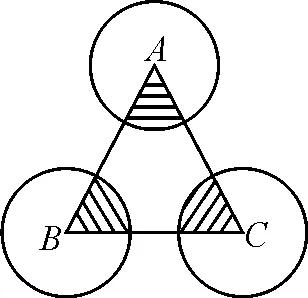
解:如圖2所示,a,-a,b,-b的大小關系是a<-b 圖2 構造如圖3所示的圖形,AB=12,AC⊥AB,BD⊥AB,且AC=2,BD=3. 圖3 設PA=x,則PB=12-x. 顯然,點C關于AB的對稱點E與點D的連線和AB的交點P即為符合條件的點. 過點E作DB的垂線交DB的延長線于點F,則 PC+PD=PE+PD=DE =13. 故所求的最小值為13. 抽象與具體的轉化策略主要指通過類比、舉例把抽象的概念和問題具體化,從而轉化為已知熟悉的內容進行解答[2].如求線段旋轉后的軌跡,可類比圓弧得到具體的公式,即可進行下一步解答.抽象與具體轉化的策略,對解答一些定義題或幾何問題有一定的幫助. 圖4 圖5 分析:這道題很容易與兩圓的位置關系相聯系,圓與圓之間的位置關系包括外離、外切、內切、內含等情況,類比正方形也存在這些位置關系,進一步分情況分別求解即可. 解: O1D=2,O2F=1,O1O2≥0. 聯系兩圓的位置關系容易得出: 當O1O2=3時,有一個公共點; 當O1O2>3或0≤O1O2<1時,沒有公共點. 整體與部分的轉化策略是指把問題所求看作一個整體或部分個體,使其問題得到簡單化從而解答.如扇形面積求解可看作一個圓的部分,根據占據圓的比例即可求出對應面積大小.這種解題策略,能使陌生未知的問題轉化為已知熟悉的內容,應讓學生重視. 例6如圖6,圓A、圓B、圓C三個圓兩兩相交,并且半徑都是0.5 cm,則圖中陰影部分面積為( ). 圖6 解:雖然無法單獨求出每一個陰影部分的面積,但通過觀察可以發現三角形的內角和為180°.三個扇形的圓心角加起來剛好是180°,又因為三個圓的半徑都相等,因此三個扇形面積之和可以轉化為求一個半圓的面積. 故選答案:B. 總而言之,轉化策略對學生學習質量與能力的提升有著重要幫助,教師應當重視多種教學方法的運用以幫助學生理解并牢固掌握轉化策略的應用,使學生能夠靈活地應用轉化策略解決各種數學問題,使復雜問題簡單化、抽象問題具體化,達到大幅提高學習效果的最終目的.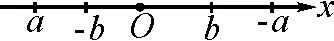
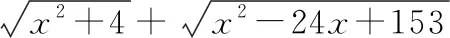


3 抽象與具體的轉化
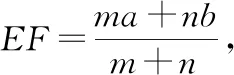

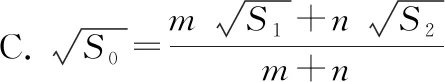
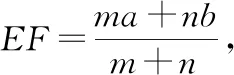

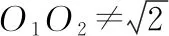
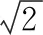
4 整體與部分的轉化
5 結語

