Python編程與算法教學的策略及指導原則

于曉雅 北京教育學院人工智能和創客教育研究中心

樊磊 首都師范大學教育學院

自信息技術新課標以Python語言作為核心編程語言推薦以來，Python編程與算法教學成為落實新課標課程目標的基礎。如何在中小學Python編程與算法教學中，落實課標精神，圍繞“算法以及基于算法的問題求解”這一核心問題，依據基礎教育階段學生特點把握適當深度和廣度，通過算法學習和實踐，為深入體會并應用計算思維（信息技術的思想、方法和手段）解決問題提供堅實基礎，實現“運用計算思維解決問題”能力培養的課程目標，是廣大信息技術學科教師共同關注的話題和主要研究點。

● 存在的問題和困難

作為普通高中信息技術新課標的重要內容，中小學Python編程與算法在教學中目前存在如下問題和困難：

第一，教學內容選擇的困難。高校中計算機及其相關專業關于算法的教學已經形成非常完備的體系，但由于中小學生與大學生在年齡和認知上存在差異,學科基礎也不同，所以基礎教育階段的算法及問題求解教學，不能是高校教學內容的簡單簡化，也不能只將其作為大學算法課程的前序準備而不涉獵本質問題。上述狀況使得中小學算法教學內容在深度和廣度方面普遍呈“高不成、低不就”的窘態。

第二，教學實踐層次的困難。首先，作為計算機科學的重要分支，算法與數學、數據結構、編程語言特性密切關聯，已經成為一個的完備的知識體系，單純講算法本身很難實施。其次，Python語言封裝了很多基礎算法的實現，而且涉及交錯復雜的概念（如數據類型、抽象數據類型），究竟是講算法的底層方面還是講高階應用難以取舍。再次，如何處理算法的直覺描述（非形式化描述）、流程圖、偽代碼（半形式化描述）和編程實現（形式化描述）之間的關系，也是教學實踐的難點。

第三，案例選擇的困難。中小學階段的算法教學是為編程教學服務的，所以必須服從編程教學的總目標：運用計算思維解決問題。但限于中小學生的認知水平和知識深度，教學案例的求解流程和問題深度很難把握，所以選擇適當的案例成為實施Python編程與算法教學的關鍵。

● 遵循原則

第一，算法應該源自學生熟悉的應用情境。

第二，在算法的選擇上，要把握好高階算法和低階算法之間的平衡。

第三，算法的目標、直觀思想以及逐步導致形式化描述的演化過程是高中（包括小學、初中）算法教學的重要部分，教學中應避免直接提出一般化、形式化的算法描述。

第四，算法中所涉及的核心思想、形式化或半形式化表示、算法推導的數學及背景知識應在學生的知識范圍內，或略微超過學生的知識范圍。

第五，算法的編程實現上，原則上不涉及較復雜或較具技巧性編程，較復雜算法可不做實際的編程實現或只做Python-like偽代碼實現，但算法作為教學案例，必須先講清楚其背后的關鍵思想。

第六，高階算法所解決的問題應具有典型性、時代性、選擇性、普適性和適用性，并且對學生的后續學習或其他學科的學習有啟示作用。

第七，在時間和條件都允許的情況下，應對解決同一類問題的、基于不同策略所實現的算法做性能比對，并挑選出較優算法。

● 實施策略

1.明晰Python編程知識進階，合理設計教學方法

在Python編程與算法教學中，要始終貫徹“需求導向、問題解決、做中學”的定位，明確學會使用函數比掌握編程技巧更重要。在設計編程案例時，要掌握輸入/輸出函數，能夠靈活運用非數值數據類型，包括字符串、列表和字典；要了解Python語言異常靈活的循環及控制結構；鼓勵教師將Python當作實現版的“偽代碼”來使用，即使確實需要用偽代碼，也建議使用Python-like風格；如果要使用Python的高級特性，編程案例應盡量依托Python語言特點，并以算法實現的需求適當漸次地引入。但筆者建議，非必要盡量不使用Python的高級特性。

2.熟悉算法策略，找準對應求解問題

算法策略是指在算法設計中所使用的問題求解的策略，是計算思維最直接、最具體的體現形式。算法策略的視角比實現算法時的具體編程實現方法在站位上要更高。

在中小學編程教育中，在算法教學里，常見的算法策略和它們用于處理的任務主要有：迭代（也稱為循環）——用于處理重復性的任務；遞歸——用于完成迭代的一種高效方法；蠻力法——在沒有更好的辦法而且計算資源（時間和空間）允許的前提下，可以嘗試采用的求解問題的方法；回溯——用于測試不可行的選擇，目的在于盡可能排除這類選擇。

● 案例解析

算法以及基于算法的問題求解是計算機科學的最重要的組成部分，也是信息技術新課程最基本、最核心的內容，算法教學中教學案例的選擇是最重要的關鍵點。下面，筆者以斐波那契數列的問題解決路徑為例，解析在上述原則和策略的指導下，如何實施Python編程和算法教學。

1.構建問題場景

斐波那契數列從0和1開始，之后的斐波那契數列系數就由之前的兩數相加。高中數學必修五在講解數列前n項和的課后資料中提到了斐波那契數列，作為數學知識生活化、發展學生抽象思維能力的拓展。

斐波那契數列（Fibonacci sequence）因為相鄰兩項的比無限趨近于黃金比等性質，又稱黃金分割數列。它是意大利數學家萊昂納多·斐波那契（Leonardoda Fibonacci）以兔子繁殖為例子而引入，故又稱為“兔子數列”。假設一對剛出生的小兔子一個月后能長成大兔子，再過一個月便能生下一對小兔子，此后每個月生一對小兔子。如果不發生死亡，一年內逐月的小兔子對數是一組非常特殊的數字：1，1，2，3，5，8，13，21，34，55，89，144，……不難發現，從第三個數起，每個數都是前兩個數之和，這個數列稱為斐波那契數列。

在現代物理、準晶體結構、化學等領域，斐波那契數列都有直接的應用，斐波那契數列的通項公式表示如圖1所示的公式（1）。

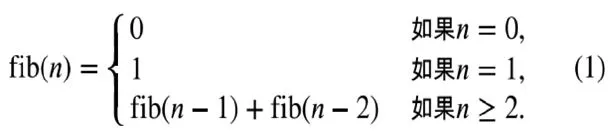
圖1

在算法教學中，斐波那契數列是最簡單的遞歸定義函數，因此非常適合用來說明實現基本遞歸算法的方法。

2.簡單遞歸實現算法

斐波那契數列的Python實現所需基本知識包括：使用if語句實現簡單迭代/循環、自定義函數、函數的遞歸定義。

斐波那契數列本身就是用遞歸形式定義的，Python是函數式編程語言，支持函數的遞歸定義，即函數體的內部包含對函數本身的調用。因此，公式（1）可以轉換為一個合法定義的Python函數，并嘗試讓學生輸出一些可很快通過人工驗證的值（不要太大）（如圖2）。

圖2

可以注意到，在計算最后一個值時是需要一點時間的。在上述的遞歸調用中，很多中間值要重復計算。如圖3所示，在計算fib_1（4）時，fib_1（2）就重復計算了2次。顯然，n的值越大，在計算fib_1（n）的過程中，需要重復計算fib_1（k）（k＜n）的次數就越多。

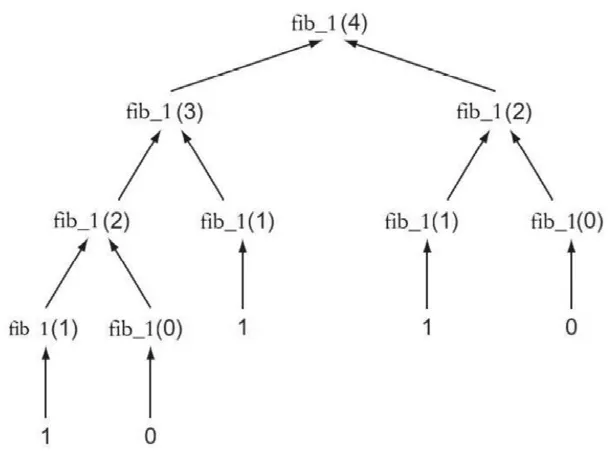
圖3

3.動態規劃優化遞歸算法

為了優化斐波那契數列的遞歸實現，一個最簡單的方法就是在每次計算中，將前面已經計算過的值“記憶”下來，不再重復計算。這種在計算過程中使用記憶的機制可以有效避免重復及浪費資源，是所謂動態規劃方法的一個最簡單的例子，動態規劃就是指資源的動態再分配。動態規劃實現需要涉及如下Python知識：Python字典、Python的Dict內建對象（一種特殊的Python字典）、對迭代器使用if語句。圖4所示代碼是一個帶有記憶的版本。

圖4

作為對比，計算fib_2（20）會產生fib_2（）的39次自調用；而若使用fib_1（），則計算fib_1（20）會產生21891次調用。

在Python中，任意對象只要定義了某種＿next＿（）方法，就是一個迭代器。因此，Python中的容器類數據類型，如列表、元組、字典、集合、字符串等，都可以用于創建迭代器。有了迭代器的概念，迭代的概念就比較容易理解了：迭代就是從迭代器中依次抽取元素的過程。

4.裝飾器優化遞歸算法

Python有一個內建的“裝飾器”（decorator），可用于自動記憶任何函數。通過使用這個裝飾器，計算斐波那契數列的函數可以更加簡化。

以下實現使用Python的高級特性——Python裝飾器語句。簡單地講，裝飾器就是在不改變原來函數代碼的情況下，給其增加一些附加功能，如上面記憶函數中間值的功能。

下頁圖5代碼實現的函數fib_3（）與fib_1（）幾乎完全相同，但使用了裝飾器@functools.1ru_cache（），其中maxsize屬性用來指示在函數的最近調用中應該緩沖多少次，設置maxsize=None表示對次數不做限制。

圖5

5.使用元組拆包優化遞歸算法

元組拆包就是將元組中的元素分別賦給變量。利用Python的元組拆包技巧可給出斐波那契函數的一個性能更高的實現（如圖6）。

圖6

在本例中，語句“last，next=next，last+next”實現將last的值更新為next的值，而將next的值更新為“last+next”的值，就是一個元組拆包。使用拆包技巧，計算fib_4（）只需循環n-1次！

6.斐波那契數列生成器-循環結構

到目前為止，所寫的函數只能產生特定位置上的斐波那契數的值，如果要一次性將到某個值為止的整個斐波那契數列都輸出，可以使用一個簡單循環（如圖7）。

圖7

7.尋找更多優化策略

教師可以引導學生繼續進行拓展練習，如探索斐波那契數列利用矩陣非遞歸化優化,也可以探索斐波那契數列與黃金分割的關系，或者使用動態規劃優化函數fib_up_to（）等，提升學生學習興趣，培養精益求精探索的創新精神。