機車車輛齒輪軸裂紋的傳動系統振動特性分析

金 鑫

（天津濱海新區軌道交通投資發展有限公司，天津 300457）

1 研究背景

齒輪傳動作為常見的機械設備動力傳動系統之一，廣泛應用于航空航天、軌道交通、切削機床等精密設備中。機車車輛中的齒輪傳動系統本身結構復雜，長期服役于高速、重載等惡劣工況，容易導致系統中各類故障的發生。當齒輪傳動系統出現故障時，齒輪副將會產生傳動誤差和齒輪側隙，進而導致機車車輛箱體振動加劇、零部件異常磨損及傳動平穩性惡化等一系列問題。因此，研究齒輪傳動系統故障對機車車輛系統動力學行為的影響，將對機車車輛安全運行起到至關重要的作用。

目前，國內學者就齒輪傳動系統零部件故障對傳動系統動力學行為的影響進行大量研究。X.He 等研究齒輪偏心狀態下齒輪嚙合時變剛度對傳動系統動力學行為的影響。Wen Liu 等利用有限元分析方法和試驗測試研究斜齒輪偏心對于齒輪箱振動特性的影響，結果表明偏心距對箱體整體的振動特性具有較大影響。馬登秋等利用Adams 建立偏心激勵作用下的圓柱齒輪動力學模型，對主從動輪不同偏心工況進行仿真分析，探究齒輪偏心量對傳動系統平穩性的影響。Y.Lin 等研究不同裂紋類型對齒輪傳動系統振動響應的影響，結果表明旋轉頻率與扭轉振頻率的結合頻率對含斜向裂紋齒輪傳動系統的振動響應較為明顯，而對含橫向裂紋的傳動系統并不明顯。R.Shao 等通過建立齒輪齒根裂紋動力學模型，研究齒根裂紋長度與裂紋位置對齒輪固有頻率和模態的影響。邵毅敏等通過建立輪齒剝落的齒輪系統動力學模型，分析齒面剝落在嚙合過程中邊緣接觸力變化情況，研究齒面剝落對齒輪傳動系統動態特性的影響。H.Jiang等考慮齒面剝落對齒輪系統時變摩擦力和時變剛度的影響，建立齒面剝落的傳動系統耦合動力學模型，研究齒面剝落對齒輪傳動系統動態特性的影響。上述研究對了解各種故障下齒輪傳動系統的振動特性和優化機車車輛的運營維護具有重要意義。

綜上所述，目前國內外對齒輪傳動系統的研究主要集中在齒輪本身故障對傳動系統動力學響應的影響，對齒輪傳動系統中齒輪軸故障對傳動系統動態特性研究較少。然而在機車車輛齒輪傳動系統服役過程中，齒輪軸長期處于高速重載工況，齒輪軸容易出現裂紋等損傷。當齒輪軸出現裂紋故障或失效時，且難以通過檢測手段進行有效測試，這將嚴重威脅機車車輛運行安全。為揭示齒輪軸裂紋對系統動力學行為影響，本文以機車車輛齒輪傳動系統為研究對象開展研究。首先，建立正常齒輪傳動系統動力學模型、齒輪軸裂紋傳動系統動力學模型及整車車輛系統動力學模型。該模型中綜合考慮齒側間隙、齒輪時變嚙合剛度、軌道不平順和輪軌接觸等非線性因素。然后，通過齒輪嚙合、懸掛系統及輪軌關系實現齒輪傳動系統與機車車輛系統的動態耦合。最后，從時域及頻域角度詳細分析齒輪軸裂紋和驅動扭矩對機車車輛齒輪傳動系統動力學行為影響。

2 動力學模型

2.1 齒輪傳動系統模型

基于多體動力學和車輛系統動力學理論，利用SIMPACK 多體動力學仿真軟件建立考慮齒輪傳動系統的機車車輛動力學模型，包括車體、轉向架、輪對及齒輪傳動系統等。其中，齒輪傳動系統主要包括齒輪箱箱體、大齒輪與小齒輪等關鍵部件。齒輪箱一端通過懸掛系統安裝于轉向架構架上，另一端通過軸承安裝于車軸上。大齒輪與車軸過盈配合，小齒輪通過軸承安裝于齒輪箱扭矩輸入端。本文將齒輪傳動系統簡化為純扭轉系統，主要考慮大小齒輪的扭轉振動自由度，因其能夠有效反映傳動系統的動態嚙合作用，如圖 1 所示。其中，Rg、Rp分別位大齒輪和小齒輪的半徑；wg、wp分別位大齒輪和小齒輪轉動角速度；a為齒輪中心距。

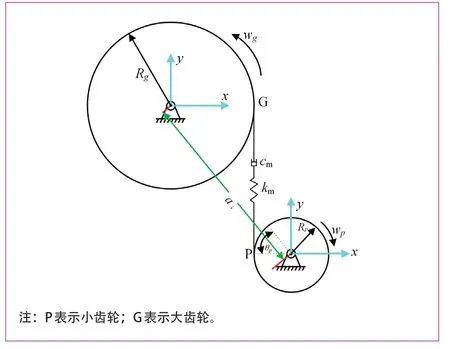
圖1 齒輪傳動系統動力學模型

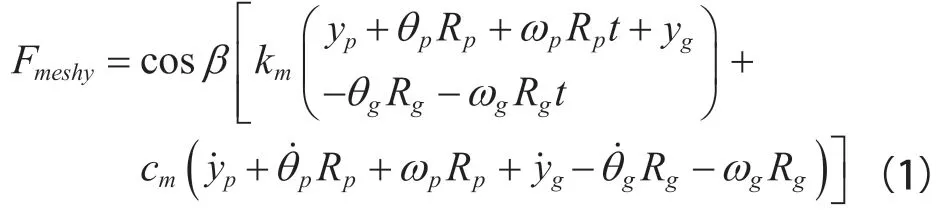
嚙合作用一般用嚙合力來表征，嚙合力的計算公式如下：）式（1）中，yp是對時間的一階求導；km為齒輪時變嚙合剛度；cm是嚙合阻尼；β是螺旋角；t是時間；ωp和ωg是小齒輪和大齒輪平均角速度；yp和yg分別表示小齒輪和大齒輪y方向的位移。

基于達朗貝爾原理，齒輪扭轉振動運動方程為：

式（2）、式（3）中，θp和θg分別表示小齒輪、大齒輪轉角；Ip和Ig分別表示小齒輪與大齒輪繞軸的轉動慣量；Tp和Tg分別表示施加于小齒輪和大齒輪的扭矩。

建模過程中采用SIMPACK 多體動力學軟件中的25 號力元模擬齒輪傳動系統，通過修改模型參數定義齒輪的幾何外形，同時把齒側間隙影響納入考慮范圍。該方法能夠有效反映齒輪時變嚙合剛度、齒側間隙等非線性因素，并考慮齒輪軸輪體的變形剛度、齒的彎曲和剪切剛度與赫茲接觸剛度的綜合影響。其中，齒輪嚙合剛度通過GB/T 3480.1-2019《直齒輪和斜齒輪承載能力計算 第1 部分：基本原理、概述及通用影響系數》標準計算。某型機車車輛齒輪傳動系統具體參數見表 1。

表1 齒輪傳動系統參數

2.2 車輛系統動力學模型

采用SIMPACK 多體動力學軟件，建立機車車輛整車動力學模型，然后將齒輪傳動系統集成于車輛動力學模型中。建立的整車動力學模型主要包括車體、轉向架、輪對、電機、齒輪箱及齒輪等關鍵部件。車體兩端通過二系懸掛支撐于轉向架構架上，轉向架構架通過一系懸掛支撐于輪對上。車輛各部件之間的懸掛通過力元進行模擬。齒輪箱小齒輪端懸掛于構架，大齒輪端通過軸承直接安裝于輪對。電機一端懸掛于構架，一端通過軸承安裝于輪軸。小齒輪通過軸承安裝于箱體，大齒輪與車軸過盈配合。此外，小齒輪與電機轉子之間通過扭轉彈簧力元模擬。輪軌縱向作用通過 Polach 模型模擬，輪軌法向作用通過非線性赫茲接觸理論計算。

建立的三維車輛動力學模型中每個部件最多考慮6個獨立的自由度，包括縱向、橫向、垂向、側傾、俯仰和橫擺運動，各部件自由度具體情況如表 2 所示。整車系統運動方程可以表示為：

表2 車輛系統各部件自由度

式（4）中，M 為質量矩陣；C 為阻尼矩陣；K 為剛度矩陣；x（t）為位移坐標列向量；F（t）為外部激勵列向量。

2.3 齒輪軸裂紋模型

齒輪軸裂紋可通過開閉模型進行模擬，其安裝齒輪位置垂向的時變支承剛度計算表達式為：

式（5）中，ΔKz為裂紋導致的軸對垂向的抗彎剛度變化；Kzc為裂紋全閉時軸對垂向的抗彎剛度；Kzo為裂紋全開時軸對垂向的抗彎剛度；為小齒輪轉角；θ為軸裂紋的初始位置角。根據軸裂紋的“呼吸式”特性可知，當裂紋全閉時與軸無裂紋時的抗彎剛度相同。基于材料力學，小齒輪安裝結構等效于小齒輪懸掛于懸臂梁上，其抗彎剛度計算表達式為：

式（6）中，F為小齒輪垂向載荷；ωd為小齒輪安裝位置的撓度。因此，Kzt和Kzo可由下式分別計算：

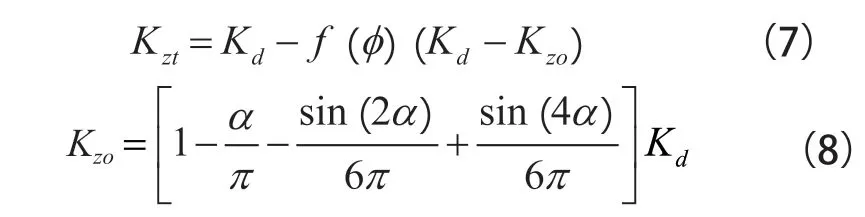
式（8）中，α為裂紋的圓心角之半。基于上述公式，計算主動輪軸在無裂紋及裂紋長度分別為30 mm、40 mm和50 mm 下歸一化剛度變化，結果如圖2 所示。

圖2 小齒輪軸在不同裂紋長度狀態下的剛度

3 模型驗證

為驗證所建模型的有效性，實驗人員開展機車車輛線路試驗，通過傳感器采集齒輪箱體振動加速度信號。試驗過程中，采集車速分別為60 km/h 和80 km/h 的數據，采樣頻率為40 kHz。于此同時，同步提取車輛系統動力學模型中齒輪箱箱體上的振動加速度。

對試驗與仿真所得振動加速度進行時域對比，所得結果如圖3 所示。車速60 km/h 時，仿真和線路試驗得到的齒輪箱體的加速度均方根值分別為0.9 m/s2和 0.8 m/s2。車速80 km/h 時，仿真和線路試驗得到的齒輪箱體的加速度均方根值分別為1.3 m/s2和1.2 m/s2。在車速為60 km/h 和80 km/h 時，仿真和試驗的誤差均較小。因此，仿真與線路試驗的結果基本吻合，由此可見，建立的動力學模型能夠有效地反映齒輪傳動系統的振動特性。

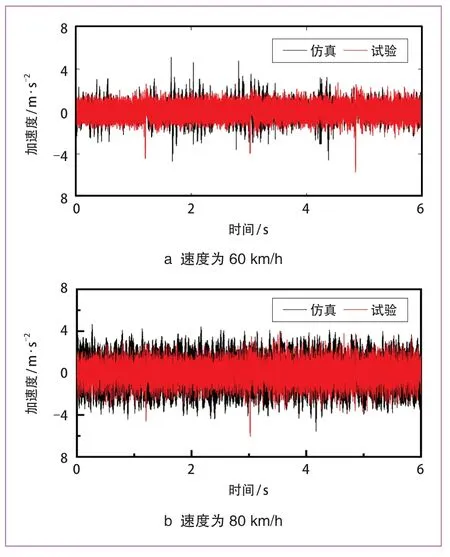
圖3 仿真與試驗振動加速度結果對比

4 仿真結果與分析

為系統研究機車車輛齒輪裂紋故障程度和驅動扭矩對傳動系統振動特性影響，基于所建立的機車車輛動力學模型，設定機車車輛運行速度為80 km/h，在齒輪扭矩T分別為1 000 N · m、2 000 N · m 和3 000 N · m 下，探究齒輪軸裂紋長度L分別為0 mm、30 mm、40 mm和50 mm 時齒輪箱體振動加速度時頻域特性。其中，仿真時長為15 s，模型采樣頻率為5 kHz，加速度測點如圖4 所示。

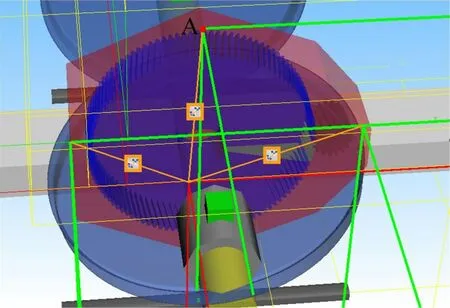
圖4 箱體測點位置

4.1 齒輪傳動系統振動時域特性

4.1.1 裂紋長度對時域特性影響

齒輪軸裂紋的出現將對機車車輛安全運行帶來極大威脅，在故障出現的初期，往往因故障特征微弱而導致人們難以發現。因此，探究不同裂紋長度齒輪時域特性差異將對發現早期故障有極大幫助。基于所建立的機車車輛動力學模型，設定機車車輛運行速度為80 km/h，仿真時長為15 s，模型采樣頻率為5 kHz，以驅動扭矩為3 000 N · m 為例，對比齒輪軸裂紋長度L分別為0 mm、30 mm、40 mm 和50 mm 下齒輪箱振動加速度信號，結果如圖5 所示。當齒輪軸出現裂紋時，振動加速度信號與無裂紋出現時相似并無明顯沖擊現象，且各自加速度幅值均在±10 m/s2以內。因此，單從振動加速度時域信號角度無法判斷齒輪軸是否出現裂紋。

圖5 不同裂紋長度振動加速度信號

為進一步分析不同齒輪軸裂紋長度下振動信號演變，計算在不同齒輪軸裂紋長度下齒輪箱振動信號的有效值與峰峰值，結果如圖6 所示。

圖6 不同裂紋長度時域特征變化

由圖6 可知，振動信號有效值與峰峰值均有相同的變化趨勢。當齒輪軸裂紋長度為0 mm 時，有效值與峰峰值均較小。當齒輪軸出現裂紋時，有效值與峰峰值均有一定增加，當裂紋長度由30 mm 加劇至40 mm時，振動信號有效值與峰峰值雖有所增加，但增加幅度較小；而當裂紋長度由40 mm 增加至50 mm 時，有效值與峰峰值急劇增加。具體變化情況為：當裂紋長度由30 mm 增加至40 mm 時，有效值與峰峰值分別增加0.31%和1.91%，增長幅度較小；而當裂紋長度由40 mm 增加至50 mm 時，有效值與峰峰值分別增加25.31%和38.83%，增長幅度較大。結果表明齒輪軸裂紋在故障程度較為微弱時，它們的時域特征變化并不特別明顯；而當齒輪軸裂紋達到某一故障程度時，時域特征指標會發生極大變化。但此時由于齒輪軸故障程度過于嚴重，可能已經導致齒輪軸失效，這將對車輛齒輪箱故障診斷與狀態監測帶來一定的挑戰。

4.1.2 驅動扭矩對時域特性影響

為進一步探究不同驅動扭矩對齒輪箱振動加速度時域特性影響，設定機車車輛運行速度為80 km/h，仿真時長為15 s，模型采樣頻率為5 kHz，以齒輪軸裂紋長度為50 mm 為例，對比驅動扭矩T分別為1 000 N · m、2 000 N · m 和3 000 N · m 下齒輪箱振動加速度信號，結果如圖7 所示。

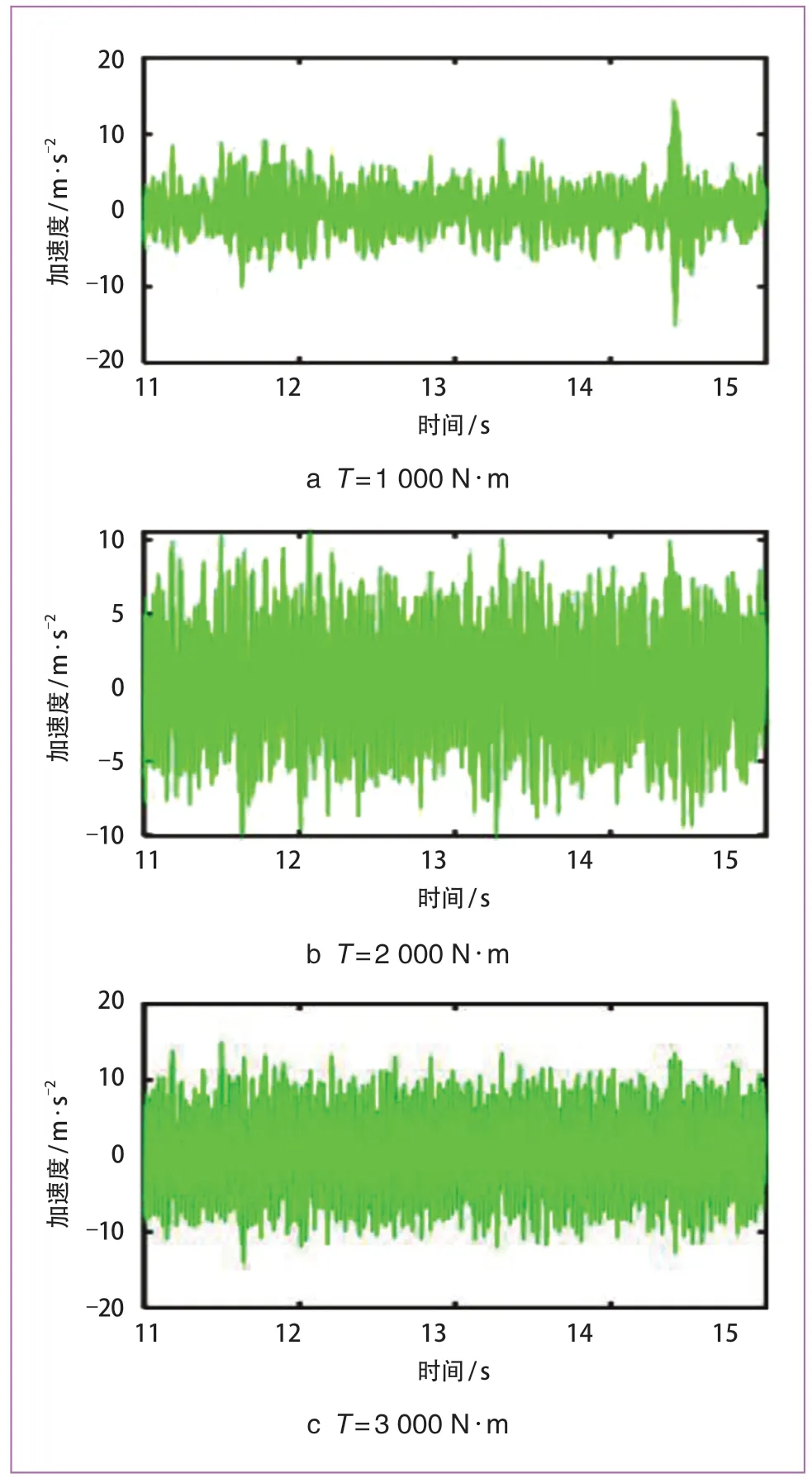
圖7 不同工況時域特征變化

當齒輪軸存在裂紋時，不同工況下齒輪箱振動加速度信號并無明顯差異，計算不同工況下齒輪箱振動加速度信號有效值與峰峰值，結果如圖8 所示。

圖8 不同驅動扭矩時域特征變化

由圖8 可知，驅動扭矩對有效值與峰峰值影響趨勢相同，即當驅動扭矩較小時，有效值與峰峰值變化較小；當驅動扭矩較大時，有效值與峰峰值變化較大。具體影響情況為：當驅動扭矩由1 000 N · m 時增加至2 000 N · m 時，有效值和峰峰值分別增加19.59%和10.99%；當驅動扭矩由2 000 N · m 時增加至3 000 N · m時，有效值和峰峰值分別增加38.57%和37.26%。結果表明，驅動扭矩對齒輪箱振動加速度時域特征有一定影響，隨著驅動扭矩的增大，有效值和峰峰值都隨之增大。但增加幅度受具體工況的影響，不能僅靠時域指標中有效值與峰峰值的變化判斷齒輪軸是否存在故障。

4.2 齒輪傳動系統頻域特性

4.2.1 裂紋長度對頻域特性影響

進一步探究齒輪軸裂紋長度對振動信號頻域特性的影響，設定機車車輛運行速度為80 km/h，仿真時長為15 s，模型采樣頻率為5 kHz，以驅動扭矩為3 000 N · m為例，對齒輪軸裂紋長度L分別為0 mm、30 mm、40 mm 和50 mm 情況下齒輪箱振動加速度信號進行快速傅里葉變換（FFT），結果如圖9 所示。

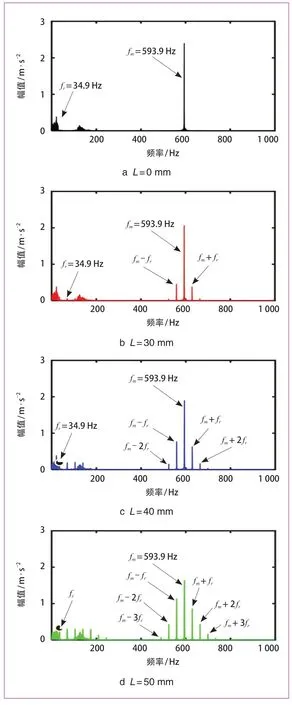
圖9 不同齒輪軸裂紋長度頻譜圖

當機車車輛運行速度為80 km/h 時，經計算可得齒輪傳動系統中主齒輪轉動頻率fr=34.9 Hz，齒輪嚙合頻率fm=593.9 Hz。由圖9 可知，無論齒輪軸出現裂紋與否，頻譜圖中均出現主齒輪轉動頻率fr。當齒輪軸裂紋長度逐漸增加時，頻譜圖中齒輪轉動頻率及其倍頻更加明顯，且所有頻譜圖中均存在一定的低頻成分，這是由于軌道長波不平順導致的。與此同時，各頻譜圖中也都出現齒輪嚙合頻率fm，當齒輪軸裂紋無裂紋時，僅存在齒輪嚙合頻率。而當齒輪軸出現裂紋時，頻譜圖中在齒輪嚙合頻率附近出現以主動輪轉動頻率為間隔的調制現象，并且該調制現象隨著齒輪軸裂紋長度的增加而不斷加劇。

4.2.2 驅動扭矩對頻域特性影響

進一步探究驅動扭矩對振動信號頻域特性的影響，設定機車車輛運行速度為80 km/h，仿真時長為15 s，模型采樣頻率為5 kHz，以齒輪軸裂紋為50 mm為例，對驅動扭矩T分別為1 000 N · m、2 000 N · m 和3 000 N · m 下振動加速度進行快速傅里葉變換（FFT），結果如圖10 所示。

由圖10 可知，頻譜圖在任意工況下均出現主齒輪轉動頻率fr和齒輪嚙合頻率fm，在驅動扭矩T分別為1 000 N · m、2 000 N · m 和3 000 N · m 時，嚙合頻率fm幅值分別為0.64 m/s2、1.19 m/s2和1.66 m/s2，因此，隨著齒輪扭矩的增加，齒輪嚙合頻率的幅值也不斷增加。當齒輪軸出現裂紋故障時，無論何種工況，頻譜圖中在齒輪嚙合頻率附近均出現以主動輪轉動頻率為間隔的調制現象，且這種調制現象隨齒輪扭矩的增加而不斷增加。

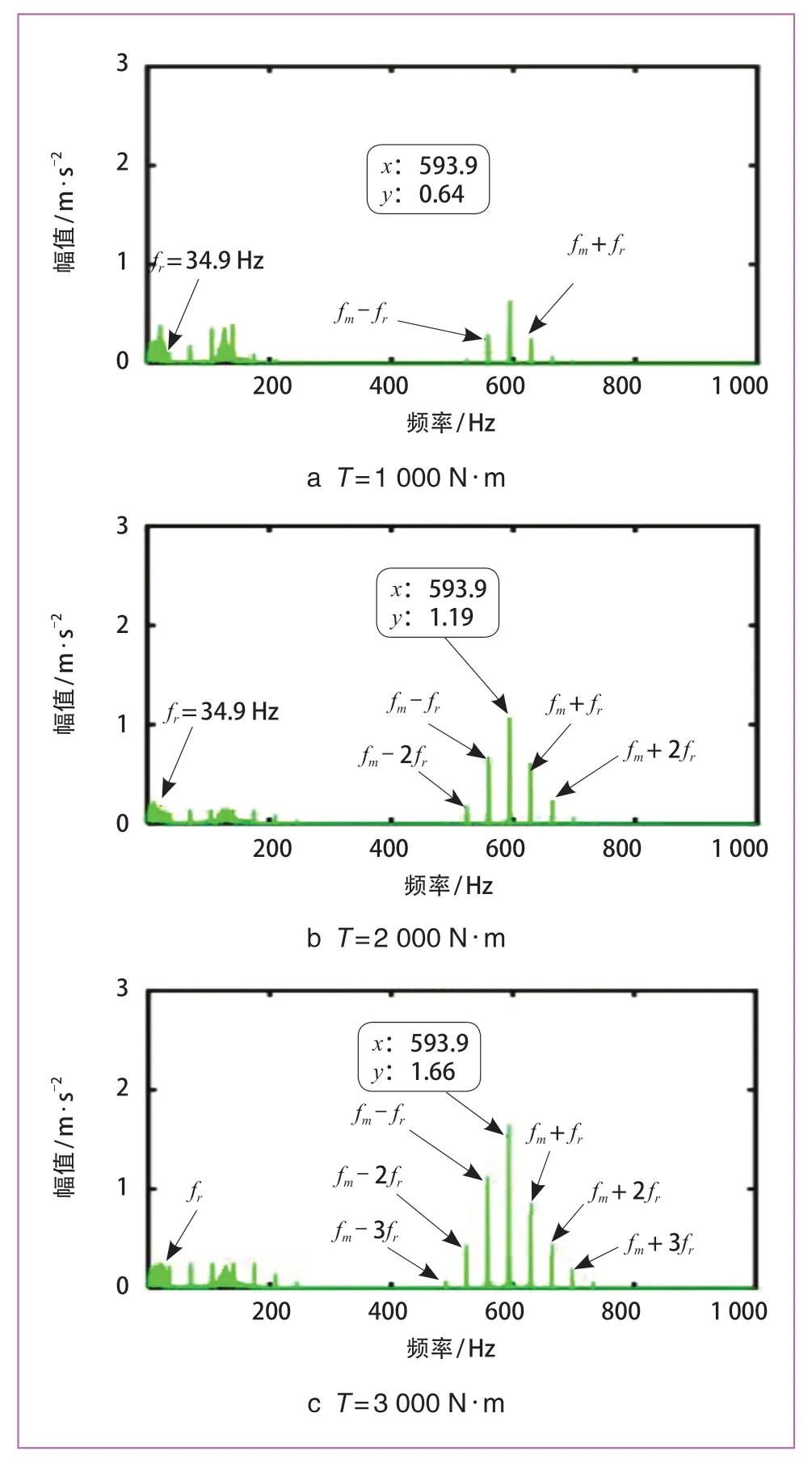
圖10 不同驅動扭矩下振動信號頻譜圖

5 結論

基于齒輪傳動系統及車輛系統動力學理論，本文建立包含齒輪傳動系統的機車車輛動力學模型，模型充分考慮齒側間隙、時變嚙合剛度和軌道不平順及輪軌接觸等非線性因素的影響，并通過機車車輛線路試驗驗證所建模型的有效性。同時通過仿真模擬探究齒輪軸不同裂紋長度、不同驅動扭矩下齒輪箱箱體振動特征，并從時域和頻域角度分析齒輪箱振動特性的影響規律。得出結論如下。

（1）齒輪軸裂紋故障的出現會使得振動信號的有效值和峰峰值增大，且裂紋故障程度會影響時域指標變化程度。當裂紋故障由30 mm 增加至40 mm 時，有效值與峰峰值分別增加0.31%和1.19%；而當裂紋故障程度由40 mm 增加至50 mm 時，有效值和峰峰值分別增加25.31%和38.83%。

（2）齒輪軸存在裂紋時，驅動扭矩的增大會使得振動信號有效值和峰峰值增大。當驅動扭矩由1 000 N · m時增加至2 000 N · m 時，有效值和峰峰值分別增加19.59%和10.99%；當驅動扭矩由2 000 N · m 時增加至3 000 N · m 時，有效值和峰峰值分別增加38.57%和 37.26%。

（3）無論齒輪軸是否出現裂紋，其加速度頻譜圖中均出現驅動軸轉頻及其倍頻。當齒輪軸出現裂紋時，頻譜圖中在齒輪嚙合頻率附近出現以齒輪轉動頻率為間隔的調制現象，并且調制現象隨著齒輪軸裂紋長度的變大而不斷加劇。

（4）齒輪軸存在裂紋時，當驅動扭矩增加時，頻譜圖中嚙合頻率幅值也會增加，且嚙合頻率和轉動頻率調制現象也會更加明顯。