高三數學微課教學的實施策略

閆沛蓮

(甘肅省蘭州第一中學， 甘肅 蘭州 730030)

高三數學教學時間緊、任務重．教師需要有效整合知識，引導學生主動分析探究問題，構建高效課堂．微課教學方式是針對學生學習中需要解決某一問題或某一知識點的微專題復習課．學生學習過程中的問題和困惑都能在微課中及時有效地得到解決，從而促使學生的知識體系更加系統，思維方法更趨完善．同時，讓學生領略數學魅力，體會解決問題的樂趣，培養學生主動學習、自主探究精神，提高學生的學習能力，提升學生的數學素養[1]．那么微課的選材從哪里來？如何有效實施微課教學？本文就高三數學微課的實施策略，從以下六個方面予以闡述．

一、一題多法，發散思維

由于學生的個體差異，學生對知識掌握程度不同，認知水平和思維能力也不同,審題時對同一個問題的分析角度不同，組合信息后就可能得到不同的解題思路，從而運用不同的解題策略和解題方法．教師在課堂教學中要善于發現和有效利用這一類問題，通過微課教學引導學生多維發散思維，并加以對比分析，最終讓學生學會選擇最優化的解題思路和方法，在培養學生發散性思維能力的同時，提高學生的解題能力．

例如，2017年文科考題：已知函數f(x)=(1-x2)ex．x≥0時，f(x)≤ax+1，求實數a的取值范圍．

此題解法較多，可以用分離參數法(結合洛必達法則)、構造函數法(移項構造新函數并研究其單調性)、數形結合法(兩個函數圖像間的關系)和放縮轉化法．不等式恒成立問題是高三教學和高考的重點內容，高三教師各有心得，因此這里不再一一贅述這道題的詳細解答過程，感興趣的教師可以查詢文后參考文獻《不等式恒成立問題的求解策略》[2]．

二、一類多法，觸類旁通

高三數學教學中，常常會涉及一類多法的問題，即同一類目標問題，卻有不同解題方法,那么什么條件下運用什么方法，學生如何選擇呢？這就需要教師整合設計這類問題的微課，歸納總結同類問題的各種不同的解答方法，集中對比講解，引導學生辨析條件，學會選擇簡單有效的方法快速解決問題．如解析幾何中的直線過定點問題，舉例如下:

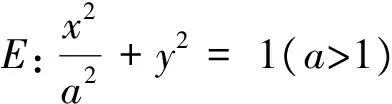
(1)求E的方程；

(2)證明：直線CD過定點．

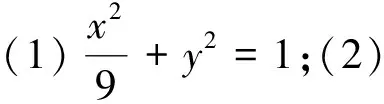
(1)求橢圓的標準方程；

(2)設直線l不經過P點且與橢圓相交于M，N兩點,若直線PM與直線PN的斜率之和為1，問：直線l是否過定點？證明你的結論．

(2)設M(x1，y1)，N(x2，y2)，當直線l的斜率不存在時，由直線PM與直線PN的斜率之和為1可解得x1=-4，不符合題意；

當直線l的斜率存在時，設直線l的方程y=mx+n，聯立方程整理得(4m2+3)x2+8mnx+4n2-12=0，由韋達定理及已知可得(n-4m)(2n-2m-3)=0．

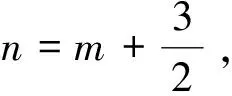
若n=4m，此時直線l：y=m(x+4)過定點(-4，0)，符合題意．

綜上，直線過定點(-4,0).

問題3(2019·全國Ⅲ卷改編)：已知拋物線M：x2=4y，直線y=-1上有一動點P，過P作拋物線M的兩條切線，切點分別為C，D.

(1)證明：直線CD過定點；(2)略.

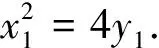
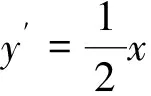
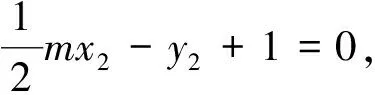
所以直線AB過定點(0，1).

以上三道題都涉及直線過定點問題，歸納出了這類問題的三種典型解法．這樣的微課設計更具針對性，既可以系統理解一類問題，也可以進行不同方法的對比探究，使學生學會分析條件辯證思維，能夠在不同條件下選擇合理有效的方法．這樣的微課素材比比皆是，如函數中的比較大小問題，二次曲線中的范圍問題，錐體柱體中的體積問題等等．只要做個有“心”的教師，善于總結題型，歸納方法，及時調整高三復習計劃，穿插微課，將一類問題的多種方法講清講透，就可以促進學生完善認知結構，切實提高學生的解題效率．

三、一類同法，強化定法

一類同法是同一知識點滲透于不同結構表述形式的題目，也可以是不同知識點之間能歸納出統一解法的問題．教師及時歸納整理這類問題，實施微課教學，就能不斷強化學生對一種特定解法的理解和掌握，有效引導學生在解決問題的過程中快速反應、識別模型，從而提高解題能力．

例如隱圓問題，隱圓問題是指題目中滿足一定條件的動點的軌跡是圓或圓弧的一類問題，是高考中常見的中等難度的問題,學生往往不能識別出題目中所隱藏的圓的信息而導致解題受阻．實施隱圓問題的微課教學，可以幫助學生辨析隱圓問題的不同模型，實現基本方法的靈活應用．

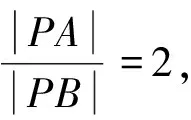
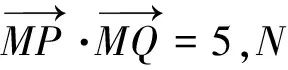
問題3：過點A(-1，3)作直線mx+y-m-3=0的垂線，垂足為點Q，若點M(4，0)，求|QM|的最大值．

問題4：已知以M(3，4)為圓心，1為半徑的圓和兩點P(-n，0)，Q(n，0)，其中n>0．若圓M上存在一點N，使得PN⊥QN，求實數n的最大值．

問題5：已知圓O的圓心為(0，0)，半徑為2，圓P的圓心為(n，3)，半徑為2．若圓P上存在點B，過點B可以作圓O的兩條切線，切點為M、N，使得∠MBN=90°，求實數n的取值范圍．

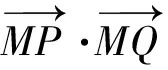
再如圓錐曲線中的最值問題，一般有代數和數形結合(建立目標函數)兩種解答方法，教師可以設計運用數形結合的思想方法解決最值問題的微課．

問題1：已知以坐標軸為對稱軸的橢圓的焦點在x軸上，焦距為2，長軸長為4，橢圓的右焦點為F，點P(1，1)，Q是橢圓上的一點，求|QP|+|QF|的最大值．

問題2：已知以坐標軸為對稱軸的雙曲線的焦點在x軸上，離心率為2，且過點P(4，6)，雙曲線的左焦點為F，M(1，3)，Q是雙曲線右支上的一動點，求|QF|+|QM|的最小值．

問題3：已知點Q(1，2)，拋物線y2=8x的焦點是F，A是拋物線上一動點．(1)求點A，使得|AQ|+|AF|最小；(2)求|AQ|-|AF|的范圍．

以上三個問題屬于同一類問題，其解法相同，都是根據圓錐曲線的定義和三點共線，運用數形結合的思想方法來確定最值位置，從而求得最值或范圍．這樣跨知識點縱向設計的微課，歸納總結出同一方法的多方位多角度應用，揭示了問題的本質，利于學生鞏固該類特定方法．經常實施這樣的微課教學，學生便能打開思維聯想的空間，舉一反三，切實提高解題效率，有效形成數學思維能力，培養數學素養．

四、多題歸一，整合知識

高三復習內容豐富，涉及題型眾多，課堂上時間有限，往往在基本運算上耗時太多會影響課堂教學效率．教師可以設計微課，將同一知識點下的不同問題歸于一個題設之下，從難度不大的基礎題出發，逐層遞進，以點帶面，提供給學生更豐富的知識平臺，能有效構建并完善學生的知識網絡，促進學生思維廣度和深度的發展,如不等式約束條件下的求目標函數最值問題，可以設計如下:

問題：設點P(x，y)滿足約束條件:

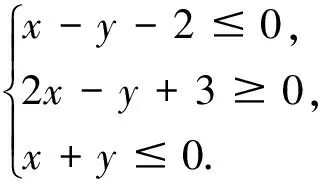
(1)求z=2x+y的范圍；

(2)求z=x2+y2+6y-2(或z=x2+y2-12y+2)的范圍；

(3)求z=|x-y+1|的范圍；

(5)若x∈Z，y∈Z，則這樣的點P共有多少個？

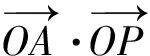
(7)若z=mx+y的最小值為-22，求實數m的值；

(8)若z=mx+y的最小值僅在點B(1，-1)處取得，求實數m的范圍；

(9)若z=mx+y取最小值的最優解有無數多個，求實數m的值．

將線性規劃的不同題型歸于一個問題之下，既有幾何意義的轉化，也有建立目標函數的代數轉化，還有含參問題的探究．如此創設螺旋式上升的問題鏈，層層遞進，可以避免無效的重復運算，加大課堂容量，讓學生在層層探究的過程中體會到學習的快樂，同時彌補自己知識的不足，促進能力的提升．多題歸一的微課，不只是講授某個知識點，而是整合完善知識網絡，促使學生理解形異而質同的問題，提高學生的歸納能力、聯想能力、辨析能力以及變式思維能力，這才是真正意義上的高效課堂[3]．

五、易混點辨析，正本清源

教師在例題教學時，以容易混淆的問題設計微課，讓學生自主審題辨析，嘗試探究，教師從旁引導，正本清源，揭示本質，促使學生明晰異同，再次碰到此類問題時能夠正確分析，不再犯錯．

(1)?x∈[-1，1]，使g(x)≥f(x)成立，求實數m的取值范圍；

(2)?x∈[-1，1]，使g(x)≥f(x)成立，求實數m的取值范圍；

(3)對?a∈[-1，1]，?b∈[0，3]，使g(b)≥f(a)成立，求實數m的取值范圍；

(4)?a∈[-1，1]，?b∈[0，3]，使g(b)≥f(a)成立，求實數m的取值范圍；

(5)對?a∈[-1，1]，?b∈[0，3]，使g(b)≥f(a)成立，求實數m的取值范圍；

(6)?a∈[-1，1]，對?b∈[0，3]，使f(a)=g(b)成立，求實數m的取值范圍．

“恒成立與能成立”問題是一個熱點問題，平時訓練經常碰到．此題中所涉及問題的轉化關鍵在于求函數的最值(或值域)，(1)(2)是要移項構造新函數求最值，學生容易轉化為分別求左右兩個函數的最值，而(3)(4)(5)是必須分別求函數f(x)與g(x)的最值，至于是最大值還是最小值，則由變量前面的存在量詞和全稱量詞來定，(6)則是轉化為函數g(x)的值域是函數f(x)值域的子集．實際教學中，由于部分學生沒能領悟問題的本質，難以保證解題的正確性．此處“借題發揮”，設計微課，把容易混淆的問題放在一起對比差異，集中辨析研究，就能讓學生理解本質、辨析不同、熟悉方法，避免學生在此類問題中再犯錯誤，進一步提高學生解題的準確性，完善學生的知識結構，提高學生的思辯能力．

六、易錯題反思，以考促學

高中數學有不少學生犯錯頻率很高的問題，教師可以積累一些學生易錯問題作為教學資源，適當地在模考前設計有關易錯題的微課,也可以集中一些易錯題考試，以考促學，暴露學生的易錯點和思維盲點，引起學生的重視，然后一究到底，充分發揮錯題的教學功能，對重點知識和典型問題重新做反復講，直到學生學會為止，努力避免學生多次出錯以及會而不全的失分現象[4]．如

問題1：解不等式lnx2<2時容易忘記定義域．

問題2：已知數列{an}滿足an+12=anan+2，且a4，a4040是函數f(x)=x2-8x+3的兩個零點，求a2022的值．

此題求解時容易忘記等比數列偶數項同號的性質．

問題3：若過點(2，0)有兩條直線與圓x2+y2-2x+2y+m+1=0相切，求實數m的取值范圍．

此題解答時容易忽略圓方程對參數m的限定條件．

類似這樣的易錯點很多，不能將錯誤簡單地歸因于學生的粗心大意或思維不完善、表述不到位，每一個錯誤都應該引起教師的高度重視．教師要將學生多次錯誤失分題型加以記錄，建立易錯題檔案，做好反饋，及時糾錯，同時也要要求學生不放過任何一個錯誤，明確自己錯誤的原因；督促學生注重積累典型錯題，勤于反思總結，彌補缺漏，以此完善知識結構，使學生的數學思維更趨嚴謹．

微課的素材，可以是知識方法與題型，也可以是某個章節的思維導圖和知識歸納，又或是高考真題的集中比較研究等等．只要教師沉入教學，善于發現，就會積累更多的微課素材．高三教師應該有意識地合理適時地組織微課教學，將離散的知識點系統地有效整合，引導學生在解決一個個問題的過程中深入理解知識和方法，實現知識間的融會貫通，使學生的數學認知結構更加系統，更趨完善，從而促進學生數學思維能力的綜合發展，為學生終身發展打下扎實的基礎．