桌面型607 機械臂工作空間及奇異位形分析

張倩玉，張宇，陳昊然，段昊宇翔

（650500 云南省 昆明市 昆明理工大學 機電工程學院）

0 引言

近年來，機器人技術在許多領域發揮著重要作用，對它的研究也越來越深入。自從機構被發明就不可避免地存在機構的奇異問題[1]。奇異位形是除了正常工作位形外的一種特殊位形，機械臂發生的奇異位形主要分為邊界奇異位形與內部奇異位形2 種[2]，它對于機械臂完成基本操作和特定任務起著重要影響。當機械臂發生奇異位形時，會對機構運動產生不利影響，如自由度變少而導致機械手無法實現某些特定運動，靈活性變差致使機構鎖死等問題。當然，奇異位形也有益處，比如利用極限位置制作一些自鎖機構等。因此，不管是從有利還是不利角度來說，對機械臂的奇異性問題展開研究都是非常必要的。

許多學者針對機械臂奇異性問題開展了深入的研究。舒曉春[3]利用雅可比矩陣分析了某工業機器人奇異位形發生的原因，提出了在實際工作過程中解決奇異位形的常用辦法；于常娟等[4]針對不同形式驅動的并聯機構,建立了雅可比矩陣，并在ADAMS 中驗證所求雅可比矩陣；蔡玉強[5]等利用微分變化法求得三自由度工業拾取機械手的雅可比矩陣,并驗證了機械手建立的正確性；張新[6]等用矢量積法解得該機器人機械臂的雅可比矩陣，對奇異位形和工作空間展開研究；李憲華[7]等建立了6R 機械臂的模型，得到了正運動學方程，并基于連桿速度法建立雅可比矩陣，得出該機械臂奇異位形的所有情況；李麗[8]等針對廣數RB20 機械臂，運用螺旋定理求出該雅可比矩陣，并對它進行了奇異位形分析；劉青松[9]等針對輪式移動抓取機械手，利用旋量法和隨機取點法解出相應的雅可比矩陣，得出奇異位形并相互印證，最后利用MATLAB 模擬求解出的奇異位形。

本文以桌面型607 串聯機械臂為研究對象，首先采用標準的D-H參數法求出正運動學方程的解，并對其驗證；然后，利用MATLAB 分析該工作空間；最后，利用通用的微分變換法得到其雅可比矩陣，并對其進行奇異位形研究，為機械臂避免奇異位形算法的研究提供理論依據。

1 機器人機械臂坐標系建立

桌面型607 機械臂運動范圍廣、運動速度快、再定位精度高，適合高速、高完成度的分揀、抓放料等工作。此機械臂是由6 個旋轉副組成，根據標準的D-H 參數法，構建連桿坐標系。圖1 為桌面型607 機械臂本體結構，圖2 為機器臂連桿坐標系。按照桌面型607 機械臂和它對應的連桿坐標系，列出此機械臂對應的D-H 參數如表1 所示。其中：d1=179 mm，a2=340 mm，a3=53 mm，d4=300 mm。

圖1 機械臂本體結構Fig.1 Robotic arm body structure

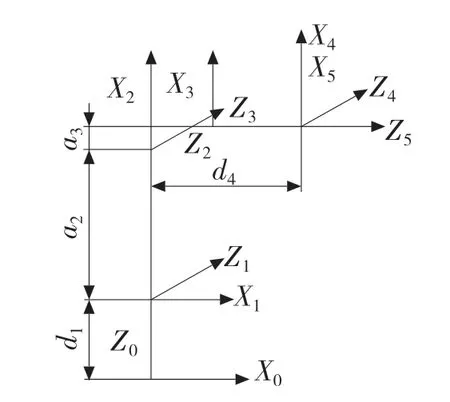
圖2 連桿坐標系Fig.2 Linkage coordinate system

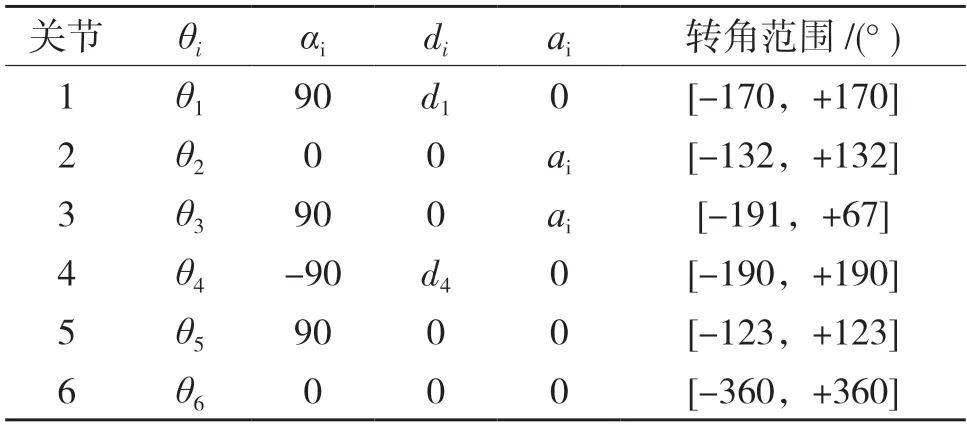
表1 機械臂D-H 參數表Tab.1 Robotic arm D-H parameters

已知關節1—關節6 的角度，即已知各關節坐標系對于基坐標系的位姿關系，則機械臂后一關節坐標系相對于前一關節坐標系的轉換關系通式為：

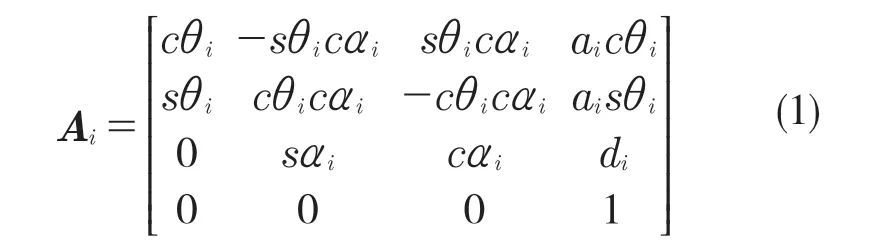
由式（1）得各連桿轉換矩陣如下：

機械臂總變換，即該末端端點的坐標系相對于該基坐標系的轉換矩陣可表示為

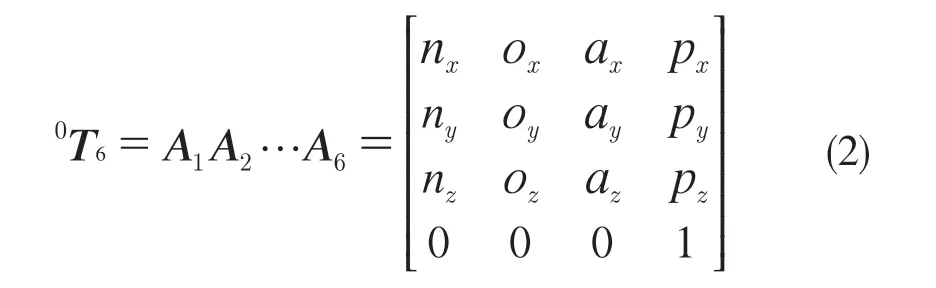
驗證正解。利用MATLAB 中的函數T=bot.fkine（zero），用Seriallink 函數得到矩陣為：

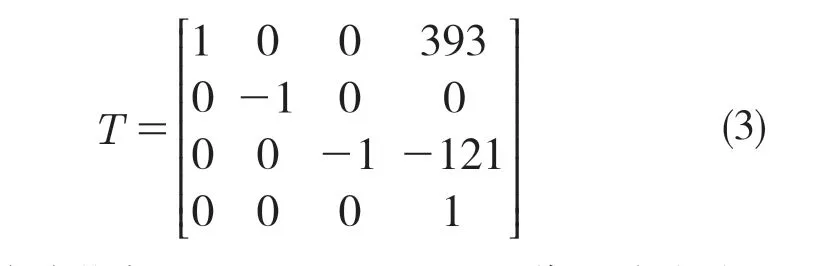
把初始關節角zero=[0 0 0 0 0 0] 代入式（2），可得矩陣0T6為

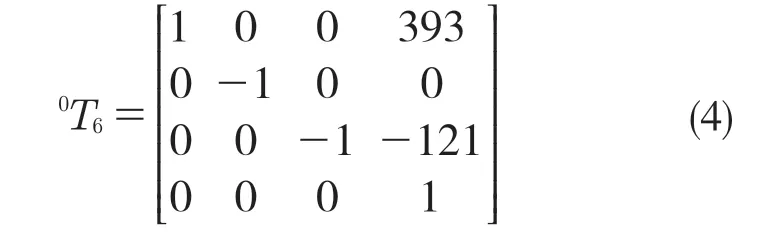
式（3）和式（4）相等，可得此機械臂正運動學求解正確。

用MATLAB 輔助模塊機器人工具箱，搭建數學模型，調用Link 函數，采用標準D-H 參數，仿真模型如圖3 所示。

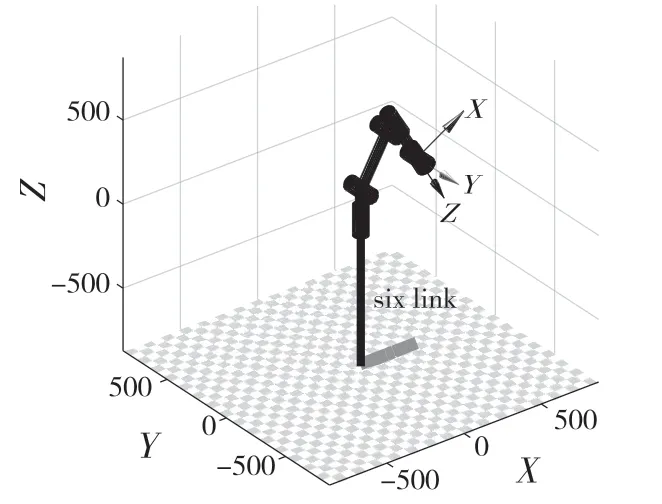
圖3 機械臂連桿仿真圖Fig.3 Simulation diagram of robot arm linkage

2 工作空間分析

工作空間是它的末端在每個旋轉關節轉角范圍內能到達的所有位姿點的表示，它對機器人機械臂控制有重要意義。因此，不管是在機器人機械臂設計還是應用方面，都要對其工作空間進行分析。有4 種方法研究工作空間：解析法、圖解法、數值法和蒙特卡洛法[10]。蒙特卡洛法是找到機械臂末端可達的區域邊界，由邊界線所組成的區域整合，然后在此區域內隨機取點，得到隨機取值點的集合，組成其工作空間。求解此機械臂工作空間的步驟如下:

（1）由式（2）解得位置向量0P6=[px py pz]；

（2）在每個旋轉關節轉角范圍內選取隨機步長變量：（θnmax-θnmin）rand（j）。有θn=θnmin+（θnmax-θnmin）rand（j）。其中，j=1，2，…，n；n=1，2，…，6。

（3）將步驟（2）中的θn代入正運動學方程，求得機械臂末端端點相對于極坐標系的位置點集合。迭代次數N的值越大，越能表達出機械臂實際工作空間的準確性。

（4）利用前3步在MATLAB里編程，然后運行，得到機械臂末端端點能達到的所有位置點，即工作空間圖，取N=20 000，N=40 000，工作空間云如圖4 所示。圖5 為N=40 000 時的3 個方向投影圖。

圖4 不同迭代次數的工作空間云圖Fig.4 Workspace cloud map for different iterations

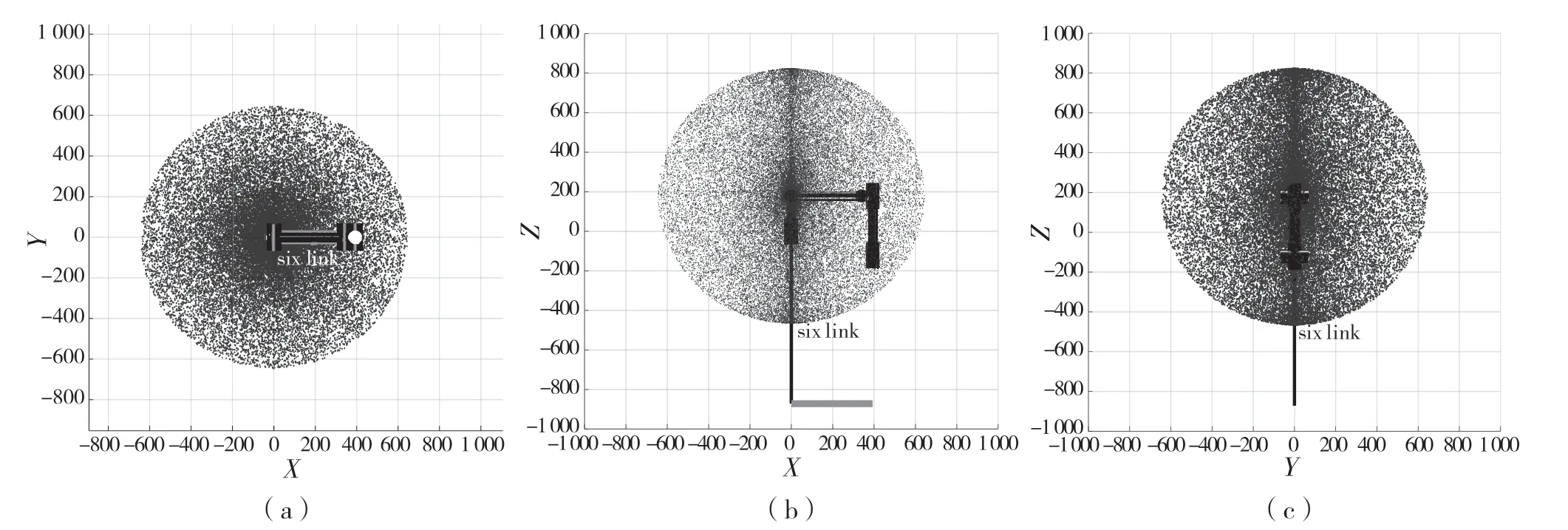
圖5 N=40 000 時的工作空間云圖Fig.5 Workspace cloud map at N=40 000

由圖4 可知，此工作空間大體可看作橢球體，圖形比較飽滿，空間中能達到的尺寸符合此機械臂的關節參數，驗證了所建機械臂對象的正確性，為之后的奇異性研究提供了試驗基礎。由圖5 可知，各投影面圖形分布均勻，無明顯空洞，得到機械臂末端點在X軸方向運動的最大范圍和最小范圍到坐標原點的距離分別為640.8 mm 和-640.8 mm，在Y軸方向運動的最大范圍和最小范圍到坐標原點距離分別為642.7 mm 和-642.7 mm，在Z軸方向運動的最大范圍和最小范圍到坐標原點距離分別為823.6 mm 和-465.6 mm。

3 機械臂雅可比矩陣的求解

雅可比矩陣表達的是其關節速度和末端端點速度的微分運動關系，因此可利用微分變換法[11-12]求出雅可比矩陣。由于此桌面型607 機械臂有6 個旋轉副，故只研究旋轉關節的雅可比矩陣求解。

若用x=（x1，x2，…，xn）T表示其末端端點的位置向量，θ=（θ1，θ2，…，θn）T表示其關節向量，則x 與θ有如下關系：

對式（5）進行微分可得式（6）：

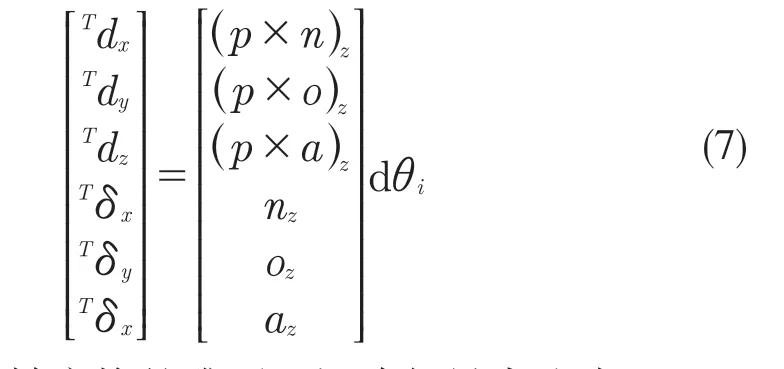
可得旋轉變換的雅可比矩陣矢量表達式：

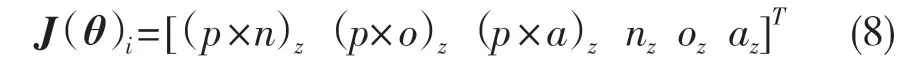
其中，（p×n）z=-pynx+pxny。同理可求（p×o）z及（p×a）z。

與關節6 的雅可比列矢量對應的變換矩陣為

分別將對應參數的n，o，a，p代入式（8），可得相應參數的雅可比矩陣的第6 列矢量：

對于關節5，可在A6基礎上求得其對應變換矩陣為

可求得關節5 對應的第5 列矢量：

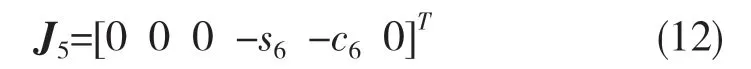
對于關節4，在A5的基礎上求得4T6：

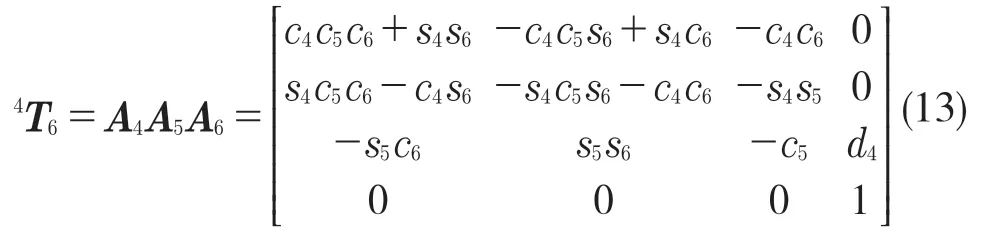
分別將對應參數的n，o，a，p代入式（8），可得相應參數的雅可比矩陣的第4 列矢量：

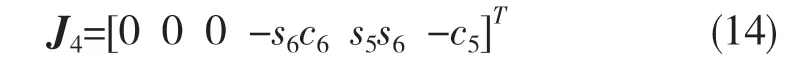
同理可求出關節3、關節2、關節1 雅可比矩陣的列矢量如式（15）—式（16）：

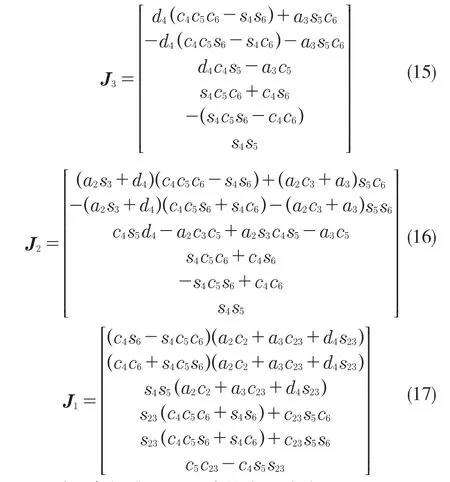
則可求得雅可比矩陣的表達式為

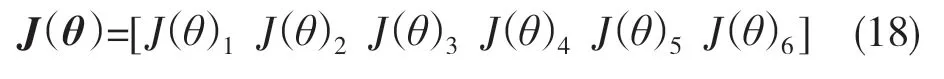
4 奇異位形識別與仿真

機械臂的奇異位置有邊界奇異和內部奇異2種。一方面機械臂每個關節都有其運動范圍，如表1 中機械臂的每個關節活動范圍所示，在這些范圍邊界處則可能產生關節的運動極限位形，即奇異位形。當機械臂對應關節分別處于θ1=±170°，θ2=±13 2 °，θ3=±6 7 °/-191 °，θ4=±190 °，θ5=±123°，θ6=±360°這些極限位置時，對應位置為極限位置奇異點，此處只列出關節1 和關節2 的極限位置，用MATLAB 仿真模擬極限位置情況，仿真結果如圖6 和圖7 所示。

圖6 關節1 邊界奇異位形Fig.6 Boundary singular posture of Joint 1

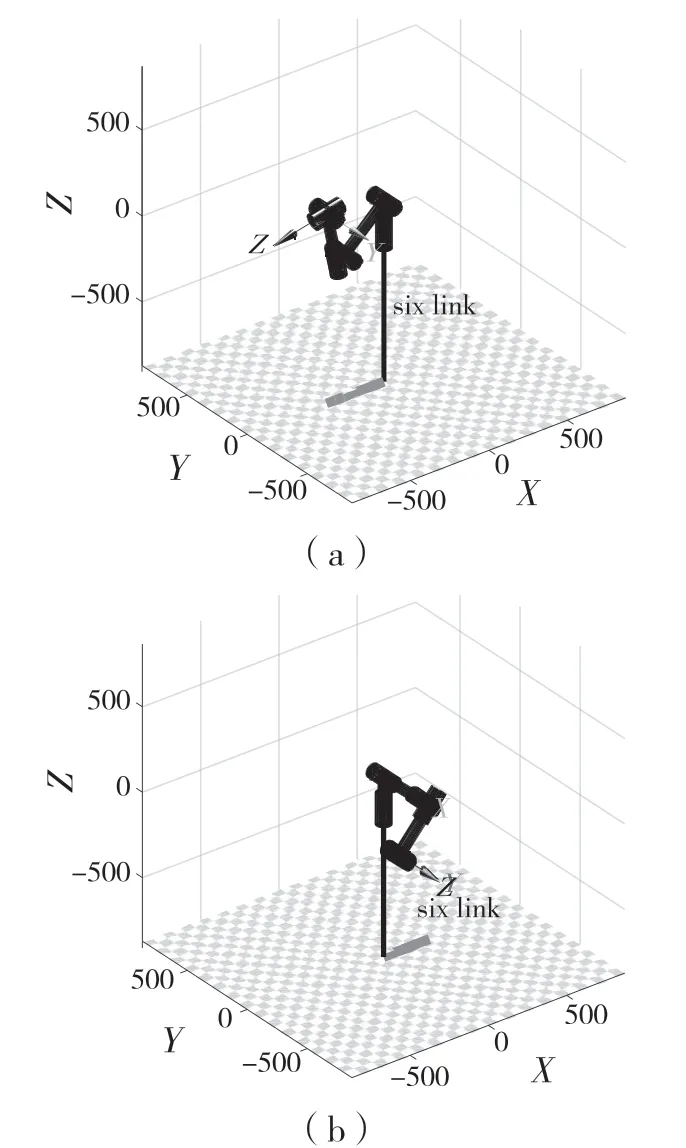
圖7 關節2 邊界奇異位形Fig.7 Boundary singular posture of Joint 2

關于內部奇異位置，由于機械臂在內部奇異位置時雅可比矩陣的行列式為零，因此令行列式（18）為零可得其內部奇異位置。令│J（θ）│=0，得到

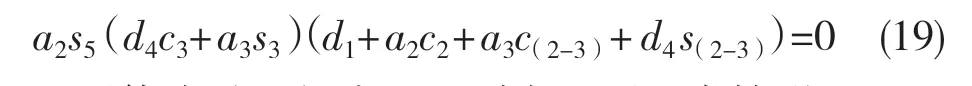
要使式（19）成立，則有以下3 類情形：

(1)當s5=0，即θ5=kπ。而θ5∈[-123 °，123°]。則θ5=0°。此種情形下，關節4 軸線與關節6 軸線處于共線狀態，用MATLAB 工具箱進行仿真分析，如圖8 所示，圖9 為共線示意圖。

圖8 關節4 和關節6 軸線共線仿真圖Fig.8 Collinear simulation diagram of axis of joint 4 and joint 6

圖9 關節4 和關節6 軸線共線示意圖Fig.9 Collinear diagram of axis of Joint 4 and Joint 6

（2）當d4c3+a3s3=0 時，得則θ3=arctan（d4/a3）。將a3=53 mm，d4=300 mm 代入，得θ3=1.395 9°。此時關節4、關節5 和關節6 的運動軸線交點與關節2和關節3的軸線屬于同一平面。運用MATLAB 對此奇異位形仿真，結果如圖10 所示，圖11 為示意圖。

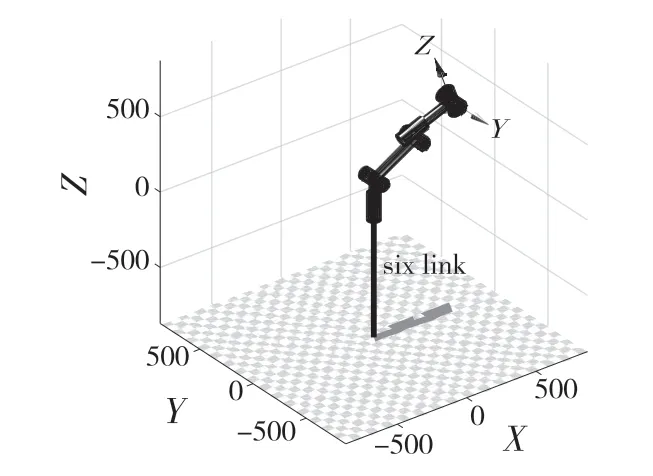
圖10 關節4、關節5 和關節6 的運動軸線交點與關節2 和關節3 的軸線屬于同一平面Fig.10 The intersections of motion axes of joint 4,joint 5 and joint 6 belong to the same plane as the axes of joint 2 and joint 3

圖11 示意圖Fig.11 Schematic diagram

（3）當d1+a2c2+a3c（2-3）+d4s（2-3）=0 時，由于其關節2 軸線和關節3 軸線平行，所以關節1 軸線和關節4 軸線是共線的，用MATLAB 進行仿真，結果如圖12 所示。圖13 為關節1、關節4 和關節6軸線共線圖。

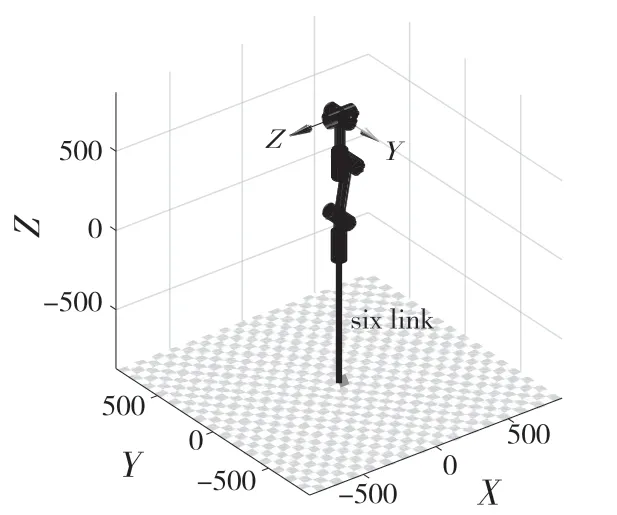
圖12 關節1、關節4 軸線重合Fig.12 Coincident axes of joint 1 and joint 4

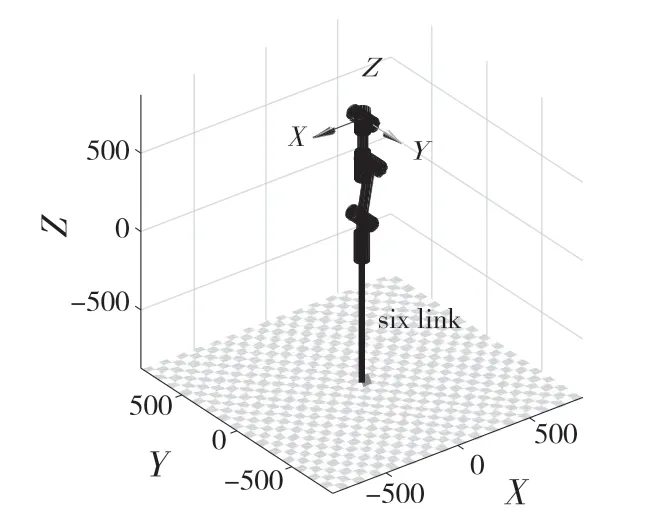
圖13 關節1、關節4 和關節6 軸線共線圖Fig.13 Collinear diagram of axes of joint 1,joint 4 and joint 6

5 結語

本文以桌面型607 串聯機械臂為研究對象，首先運用標準的D-H 參數法求得其正運動學方程的解，并對其進行驗證；其次，在MATLAB 中創建桌面型607 機械臂對象，研究其工作空間，得出其工作空間大體可看作橢球體，圖形比較飽滿，空間中能達到的尺寸符合此機械臂的關節參數，驗證了所建機械臂對象的正確性，為之后的奇異性研究提供了試驗基礎；接著利用微分變換法求出該雅可比矩陣，最后利用該矩陣行列式等于0，求得其奇異位形，并用MATLAB 進行了仿真模擬，驗證了方法的準確性。

通過分析仿真，此機械臂除了邊界奇異點外，主要存在3 種內部奇異位形。本文分析研究可幫助此桌面型607 機器人機械臂在執行任務時避免出現奇異位形，對機械臂后續避免奇異位形算法研究提供參考。