考慮區域協調的SAPF 分布式諧波動態優化治理

張巍舟，陶 駿，汪 清，吳 顯

（1.安徽大學電氣工程與自動化學院，合肥 232000；2.安徽大學電能質量教育部工程中心，合肥 232000；3.南方電網公司新型智慧城市高品質供電聯合實驗室（深圳供電局有限公司），深圳 518020）

隨著新能源的大量接入和配電網電力電子化趨勢，諧波污染的特點從傳統的數量少、分布集中轉變為數量多、分散化、全網化[1-3]。為了滿足高端制造業智能化、精密化的發展需求，建設高電能質量的優質電力園區勢在必行。

未來諧波污染將是影響園區電能質量的重要因素，傳統的諧波點對點治理方式是按照誰污染誰治理的原則，針對特定負荷污染源進行集中治理，提高電網電能質量水平[4-5]。由于配電網諧波污染所呈現的新特點，諧波傳遞引起的疊加污染危害也不容小覷，傳統的點對點治理方式的經濟性和治理效果受到限制[6-7]。在此背景下已有學者研究新的治理策略，文獻[8]的方法對并聯有源電力濾波器SAPF（shunt active power filter）并網點附近節點電壓畸變情況治理效果較好，但對線路其他節點治理效果有限；文獻[9]利用SAPF 實現諧波的分布式治理，但各個裝置獨立工作，未從全網協調角度考慮節點畸變情況。文獻[10]以全網節點電壓畸變率為目標，提出一種基于電壓檢測型有源濾波器實現全網諧波的分布式主從協同優化治理；文獻[11]建立諧波矩陣模型進行分析，利用SAPF 進行全系統優化治理，可以改善系統的整體電壓質量；文獻[12]建立分布式整流器網絡諧波模型，優化SAPF 的控制策略，實現全網諧波抑制，但文獻[10-12]均通過建模優化了SAPF 的輸出諧波電流，優化的結果依賴于模型與實際電網阻抗信息的匹配程度。

綜上，利用多個SAPF裝置，在系統層面進行分布式協調優化控制成為新形勢下諧波污染治理的關鍵手段，而網絡諧波優化治理問題是一個典型的非線性混合規劃問題[13]。通過污染建模和阻抗分析求解所得諧波治理結果依賴于模型的精確性[14-15]，若通過監測裝置獲取節點電壓數據優化SAPF 的實時輸出諧波電流，在線制定相應的諧波治理策略，減少系統的諧波污染是一條解決模型精確性不足問題的有效途徑。

本文考慮多SAPF 的分布式協調治理模式，基于諧波耦合與傳遞關系，在諧波阻抗矩陣的基礎上建立節點間諧波耦合關系，獲得諧波治理的關鍵節點即SAPF 的安裝地點；以配電網采集窗口內節點電壓數據為反饋信息，探索實時情況下節點間諧波耦合關系，根據關聯度分析結果確定各個SAPF 的治理區域，運用粒子群算法優化SAPF 的實時輸出諧波電流，達到對區域諧波污染的最優治理效果的同時實現全系統的諧波治理。

1 SAPF 布局策略

1.1 SAPF 系統側諧波治理原理

諧波源發出諧波電流在電網中傳遞的本質在于電路網絡中的電源和阻抗[16]。在合適的位置上安裝SAPF，對電網注入大小相同、相位相反的諧波電流進行抵消，從本質上實現諧波的治理。一個含有n個節點的配電網，根據配電網主要網絡元件的工作特性構建諧波模型，采用諾頓模型等效電力電子設備諧波源[17]，利用諧波網絡建模所得到諧波阻抗矩陣求解網絡的諧波潮流，即

式中：為節點i的h次諧波電壓；為諧波源節點j的h次諧波注入電流；為節點i和節點j的h次諧波互阻抗；為節點i的h次諧波自阻抗。

由式（1）可知，在n節點的配電網中，在h次諧波潮流下，諧波電流源節點j發出的h次諧波電流，通過諧波阻抗矩陣Zh可以計算得到節點i的諧波電壓，Zh體現了節點之間的諧波電壓電流耦合關系；當多個諧波源接入電網，節點諧波電壓決定于諧波源出力大小及其分布。當某個節點與其他節點表現出較強的耦合關系時，選擇在此接入SAPF并注入適量諧波電流能夠實現對區域內多個節點諧波電壓的高效治理；同時，依據節點間的耦合效應，進行配電網的治理分區，提高電網整體諧波電壓治理水平，實現多SAPF在系統側的協同。

1.2 聚類分區后選擇SAPF 安裝位置

根據SAPF 系統側諧波治理原理，需要考慮節點之間的諧波耦合關系，確定SAPF 的安裝位置和輸出容量。本文采用基于Ward距離的凝聚型聚類算法，利用系統諧波阻抗矩陣表現的節點諧波電壓、電流耦合特性，對配電網n個節點聚類劃分強耦合區域，通過計算區域內各節點耦合連接度實現SAPF的布局。

1.2.1 基于Ward 距離聚類劃分強耦合區域

本文所采用的凝聚型聚類算法步驟如下：

步驟1輸入節點阻抗矩陣后，以歐幾里得公式計算節點之間的電氣距離；

步驟2每個節點各成一類開始分類，基于Ward方法計算類與類之間的距離；

步驟3比較類間距離最小的2個類合并成為1個新類，此處的類間距離作為從劃分k到k-1個類的合并距離，并重新計算各個類之間的距離；

步驟4重復步驟3直到全部分為1類。

合并距離是指步驟3中每次合并2個類的類間距離，根據文獻[18]所述，依據Ward 距離進行類間合并相比于其他計算類間距離的方法所進行的合并正確性更高。比較每一步合并過程中的合并距離，當分區的個數從k到k-1的過程中，出現較大的合并距離，意味著此次分區的過程需要較大的合并類間距，且在此之前2個分區相互之間的距離相對較近，在這之后每次合并都需付出較大的合并距離才能完成，因此k個分區將是一個合理的劃分。

1.2.2 基于節點耦合連接段選擇SAPF 安裝位置

在劃分區域后應選擇區域內的強耦合關聯節點安裝SAPF，實現更高的治理效益。節點i在區域內的諧波耦合連接度Li[19]，以及節點i與節點j之間的電氣距離Zij,equ的計算可表示為

式中，Zi1、Zj1、…、Zin、Zjn均為諧波導納矩陣中的互阻抗。

在聚類算法中，首先，通過歐幾里得距離計算公式得到節點間的電氣距離；然后，由式（3）計算節點i與節點j之間的電氣距離Zij,equ；最后，由式（2）將節點i與所在分區內其余節點的電氣距離之和取倒數，得到節點i在區域的重要程度Li。Li的值越大，表明節點i與其余節點的諧波耦合作用越強，該節點所注入的諧波電流對其余節點的諧波電壓影響越大，是網絡中的關鍵節點。因此將此節點作為SAPF的安裝節點，實現SAPF系統性治理諧波的第1步。

2 基于動態分區的SAPF 分布式治理策略

在電網運行過程中，諧波源狀態變化和負荷投切導致諧波潮流動態變化。基于數據驅動的思想，本節研究如何根據節點諧波電壓反饋數據獲得SAPF實時控制指令，完成對多節點配電網系統性的動態治理，圖1為諧波動態治理系統。由圖1可知，協調控制器根據監測設備得到的節點諧波電壓時間序列數據進行分析和優化處理，以SAPF 安裝節點為中心劃分動態治理區域，確定節點治理權重后建立優化治理模型，實現配電網諧波動態分區治理。

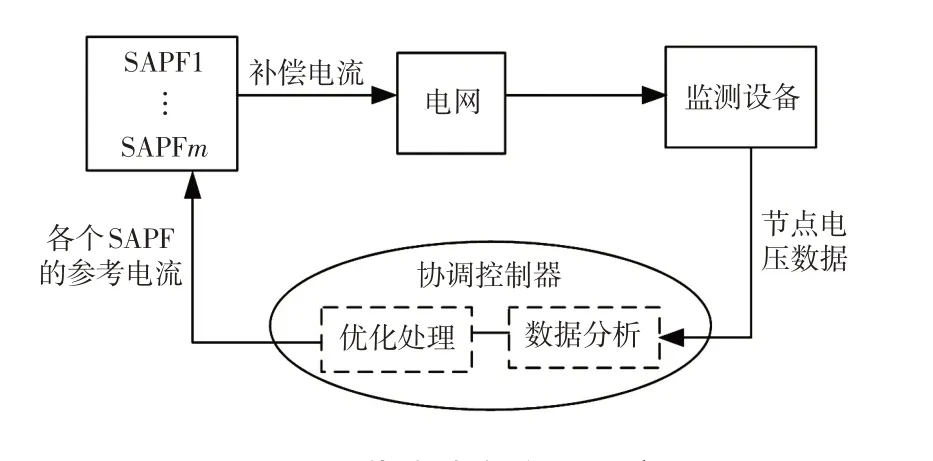
圖1 諧波動態治理系統Fig.1 Dynamic harmonic control system

2.1 數據分析過程

電能質量監測設備可以記錄節點諧波電壓時域數據。首先，采用灰色關聯分析方法[15]對比任意2個節點的諧波電壓時間序列變化的相關性獲得關聯度矩陣；其次，考慮SAPF 的安裝位置已定，運用映射型聚類分區[20]將與安裝節點關聯度高的節點劃分為一類，獲得SAPF 的動態治理區域以實現SAPF對區域內各節點的有效治理。

2.1.1 基于關聯度矩陣進行映射聚類分區

關聯度數據分析是根據因素之間發展趨勢的相似或相異程度，即“灰色關聯度”來衡量節點間的關聯程度。若2 個節點數據變化的趨勢同步程度較高，即二者關聯程度較高，則2 個節點間的諧波耦合程度越高。為了更準確地獲得分析結果，運用規范化方法將數據映射在[0-1]之間，即

式中，xi(k)為節點i在k時刻的采樣數據。

節點i在k時刻的關聯度系數εi(k)可表示為

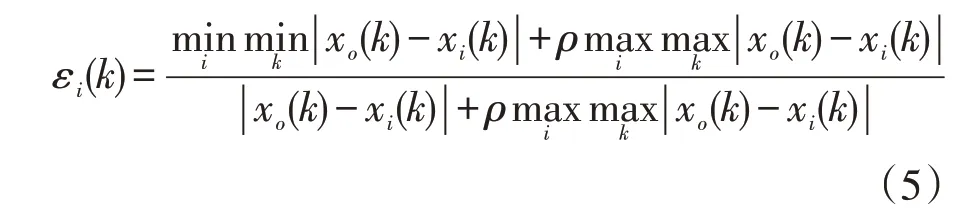
節點i的關聯度ri可表示為

式中，n為節點的個數。

在計算得到關聯度矩陣后需要對反映出的節點間諧波耦合程度進行劃分，根據映射型聚類算法處理關聯度矩陣，得到動態的治理區域。具體步驟如下：

步驟1根據第1.2 中n個節點配電網的SAPF布局策略，已知SAPF 的安裝位置和數量，以SAPF安裝位置為控制節點，進行劃分治理區域；

步驟2根據式（6）計算節點間關聯度，得到控制節點到每個被控節點的關聯度，以此作為分區依據；

步驟3比較各個被控節點到每個控制節點的關聯度，將被控節點劃分到關聯度最大的區域中；

步驟4重復步驟2～3，直到所有的節點計算完成為止。

在最后所得的分區結果中，同一分區能夠有效考慮被控節點與SAPF 安裝節點的關聯度，即2 個節點間諧波的耦合程度，保證SAPF 治理區域內節

點的耦合程度盡量高。

2.1.2 節點治理權重系數

在同一個區域內，由于各節點與SAPF 安裝節點的耦合程度不同，其治理改善程度也受到影響，同時各個節點的負荷對并網點諧波的耐受程度也不同。因此結合節點與控制節點間的關聯度和節點的負荷敏感因子作為SAPF治理各個節點的權重系數，所得到的節點權重能夠考慮到節點間諧波耦合關系和節點的負荷敏感度，避免個別節點的負荷敏感度高但耦合關系弱，出現治理效果不佳的情況。

利用綜合賦權法結合節點重要度和節點與控制節點間的關聯度，可得節點治理權重系數為

式中：ci為節點i的節點重要度；ri為節點i與所在區域控制節點之間的關聯度。

針對節點負荷設備對電網諧波敏感程度進行考察，引入節點敏感度因子α，其值反映了節點所接負荷設備對電壓畸變的敏感程度，α值越大表明該節點對畸變指標要求越高。本文采用節點敏感度因子比重的方法定義節點重要度權重系數cn，即

式中，αi為節點i的節點敏感因子。

2.2 優化模型的建立與求解

2.2.1 優化模型

根據數據分析過程中統籌全局信息所得到的分區結果和節點治理權重，在優化過程中以區域內節點平均諧波電壓畸變率為目標函數，解得SAPF的最優輸出諧波電流，以滿足各個節點的諧波治理需求，達到區域內平均諧波電壓畸變率最低。對于一個接入大量非線性負載的配電網，電網任意節點i的h次諧波電壓可以用復數形式[6]表示為

式中：為電網節點i的h次諧波電壓；為諧波電壓的實部；為諧波電壓的虛部。

根據第1節SAPF的配置模型，確定第k個節點配電網中SAPF 的安裝地點后，SAPF 的第h次輸出諧波電流可定義為

式中：m為SAPF 安裝個數；分別為SAPF 所在節點k處的輸出h次諧波電流的實部和虛部。

區域內節點i的h次諧波電壓的改善程度等于節點k所安裝的SAPF 輸出的h次諧波電流乘以節點i與節點k間的h次諧波阻抗，即

補償后的諧波電壓可表示為

2.2.2 目標函數

確定一個多節點配電網SAPF 的安裝地點，形成動態治理分區后，以并聯在系統節點上的SAPF所輸出的諧波電流為優化對象，為使區域節點電壓畸變達到最優，針對不同節點的諧波敏感度和關聯度設定各節點治理權重系數，將區域內各節點電壓總畸變率加權求和，取其最小值作為區域優化的目標函數，即

式中：fTHD,i為安裝在節點i處的SAPF 治理區域內的電壓總畸變目標函數；bi為節點i的治理權重系數，其大小由式（7）計算得到；THDu為節點i的電壓畸變率；Uh,i為節點i的h次諧波電壓；U1,i為節點i的基波電壓。

2.2.3 約束條件

SAPF 諧波補償過程中，其最大補償量不能超出容量的限值，即式中：SSAPF,i為第i個SAPF 輸出實際諧波補償容量；kSAPF,i為預留容量系數，以保證SAPF容量足以補償諧波擾動量；為第i個SAPF的額定容量；Ih,i為第i個SAPF的h次諧波電流值。

2.2.4 模型求解

采用粒子群算法求解第2.2.1 節所述的優化模型，應用監測數據針對區域的各節點諧波電壓畸變情況對SAPF 輸出諧波電流進行統一調節，實現平均諧波電壓畸變率最低，其流程如圖2 所示。圖中，U1,h，U2,h，…，Un,h為節點1，2，…，n的h次諧波電壓數據；ISAPF.1，ISAPF.2，…，ISAPF.m為所布局的m個SAPF的輸出諧波電流。

圖2 SAPF 動態治理過程Fig.2 Dynamic control process by SAPF

3 算例仿真分析

基于MATLAB 仿真軟件搭建仿真系統，設置8個節點的低壓配電網模擬園區配電網系統如圖3所示。其中，上級電網額定電壓10 kV，短路容量設為100 MVA，配電網通過1 臺10/0.4 kV，容量為1 MVA的Dyn11型變壓器連接到低壓配電網；單位長度的線路阻抗設置為0.64+j0.101 Ω，各節點之間的長度設置為50 m；對3、5、6、7、8節點均設置了諧波源，利用諾頓模型表征分散的諧波源；各節點有功功率為5 kW，無功功率為2.5 kVar；設置1、3、8節點接有敏感負荷，負荷敏感因子為7，其余為1。所得節點重要度如表1所示。

圖3 8 個節點配電網系統Fig.3 Diagram of 8-node distribution network

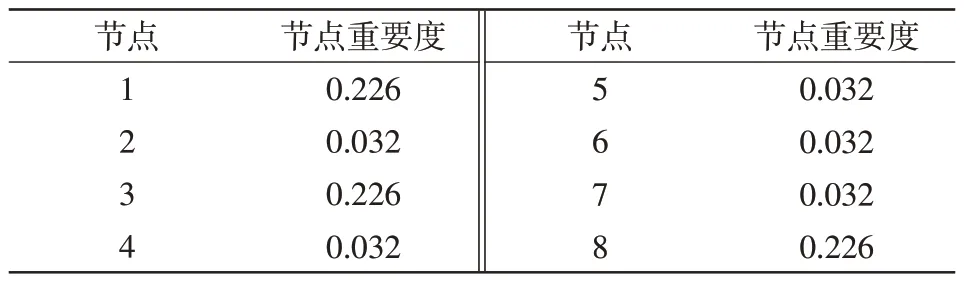
表1 節點重要度Tab.1 Importance degree of nodes

3.1 SAPF 布局選擇

采用諧波潮流建模方法和凝聚型聚類算法分區，層次聚類過程如圖4所示。由圖4可知，每次分區數減1的過程中合并成本都在緩慢升高；而分區數從2到1的過程中所需的合并成本遠大于之前的成本，由此可得分區數為2，分得的區域分別為{1，2，3，6}和{4，5，7，8}2 個區域；在區域內計算節點耦合連接度辨識得到關鍵節點分別為2和7這2個節點作為SAPF的安裝節點。

表2 區域1 節點耦合關聯度Tab.2 Coupling correlation degree of nodes in Area 1

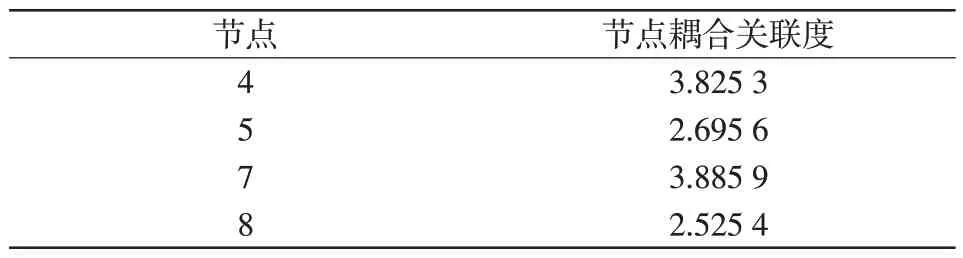
表3 區域2 節點耦合關聯度Tab.3 Coupling correlation degree of nodes in area 2

圖4 層次聚類過程Fig.4 Process of hierarchical clustering

為證明節點2 和7 選擇結果的正確性，對各個節點分別注入相同的諧波電流并紀錄其所在區域的平均諧波電壓畸變情況，如表4、5所示。由表4、5 可以看出，節點2、7 所輸出的諧波電流對各自區域的諧波電壓畸變影響最大，證明了區域關鍵節點選擇的合理性。

表4 區域1 節點平均諧波電壓畸變情況Tab.4 Average harmonic voltage distortion of nodes in Area 1

表5 區域2 節點平均諧波電壓畸變情況Tab.5 Average harmonic voltage distortion of nodes in Area 2

3.2 動態分區有效性驗證

根據園區配電網規劃背景，配電網系統的采集時間窗口設置為1 min；一個負荷數據系列包含1 440個點，參考非線性負載諧波電流的時變特性，每個諧波源隨機設定1 440 個點的變化情況；諧波源所發出的諧波電流包含5 次和7 次諧波，幅值變化范圍為基波電流的5%～15%，相位在0～2π 內隨機變化，以此模擬一個采集時間窗口內由電能質量監測裝置獲得的數據。采集各個節點的諧波電壓數據后進行關聯度分析得到關聯度矩陣如表6 所示；對關聯度矩陣進行聚類分析得到SAPF 的動態諧波治理分區結果如表7 所示。以區域電壓平均諧波含量作為目標函數，SAPF容量為約束，計算得到SAPF 的最優輸出；粒子群優化算法設定最大慣性權重ωmax為0.9，最小慣性權重ωmin為0.4，學習因子初始值為c1=c2=1.5，粒子群規模為200，最大迭代次數為150。

表6 各節點諧波電壓運行數據的關聯度Tab.6 Correlation degree of harmonic voltage operation data at different nodes

表7 動態分區結果Tab.7 Dynamic partitioning result

圖5、6 分別給出了在區域1 和區域2 單獨治理時的節點諧波電壓情況，同時設定對照組為在節點2、7 對諧波電壓就地治理；圖7 為就地治理策略和本文所提動態分區治理策略在治理前后對比情況。

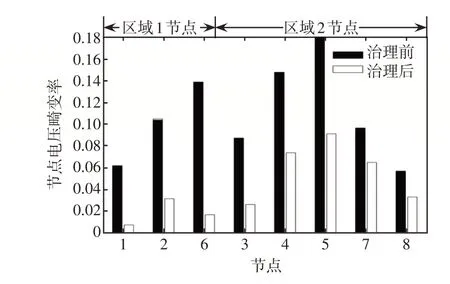
圖5 區域1 治理情況Fig.5 Control result in Area 1

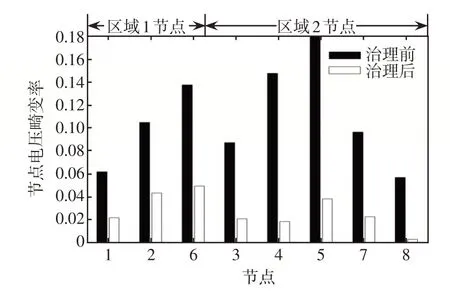
圖6 區域2 治理情況Fig.6 Control result in Area 2

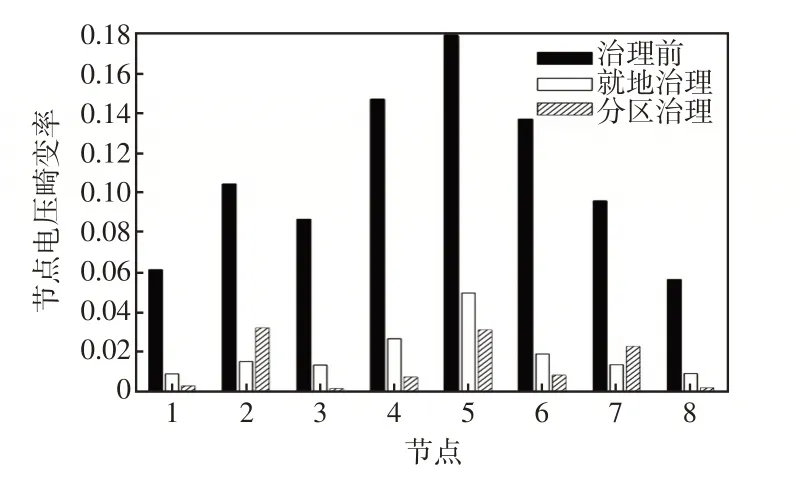
圖7 節點治理對比Fig.7 Comparison of control result at different nodes

由圖5 可知，在區域1 單獨治理時，節點1、2、6的諧波電壓畸變率得到了很好地改善，區域1節點諧波電壓平均畸變率為1.8%；區域2的節點3、4、5、7、8諧波電壓畸變率也得到了一定的改善。由圖6可知，在區域2單獨治理時，節點3、4、5、7、8的諧波電壓畸變率得到了很好地改善，區域2節點諧波電壓平均畸變率為2%；區域1的1、2、6節點諧波電壓畸變率也得到了一定的改善。

由圖7可知，在2個區域同時分區治理時，系統節點諧波電壓平均畸變率為1.2%，低于各自單獨時的節點諧波電壓平均畸變率，驗證了通過耦合特性對系統進行分區治理策略的有效性。同時可以看出在節點2、7就地治理策略中，對其他節點諧波電壓也起到很好的治理作用，治理后節點諧波電壓平均畸變率為2%，表明SAPF 布局策略的合理性；但節點5的諧波電壓畸變率仍很突出，顯示出就地治理策略仍有不足。根據本文所提出的動態分區治理策略得到的治理后各節點諧波電壓平均畸變率在1.2%，相比于就地治理更低；除了2、7 節點外其余節點的治理效果均優于就地治理，體現了動態分區治理策略的優勢。而SAPF對非本地節點治理會犧牲一定的諧波水平，因此在圖7 中節點2、7 這2 個安裝節點的諧波水平較高，但仍在諧波標準之內。同時針對敏感節點1、3、8有很好的的治理效果，表明了節點治理權重系數設定起到了很好的作用。

4 結論

本文在電力電子化配電網諧波污染情況下，利用節點間諧波耦合關系，控制多個SAPF 在系統側對諧波進行治理，提出SAPF 動態分區優化治理策略，相關仿真驗證了分區治理的有效性，得到如下結論。

（1）在SAPF 布局策略中以節點間諧波耦合關系為依據，運用凝聚型聚類分區算法并計算節點耦合連接度得到網絡中的關鍵節點，從而反映出此處輸出諧波電流對區域內其他節點諧波電壓變化影響力最大的特點。以此為SAPF的安裝位置避免了優化配置的繁重計算量，同時獲得接近最優的配置結果，為制定合理的治理策略起到了鋪墊作用。

（2）應用數據驅動的思想在多節點配電網中實現多個SAPF的系統分區協調治理。運用灰色關聯度算法處理諧波電壓反饋數據，關聯度矩陣反映了實時變化的節點諧波耦合關系。因此根據節點間關聯度劃分SAPF 動態治理區域，在保證區域內節點與SAPF安裝節點的強耦合特性的同時，建立SAPF區域優化治理模型，解決了在電力電子化諧波污染背景下，傳統點對點治理策略的低效和不經濟的缺陷。