巧思維切入，妙視角拓展
——一道向量題的深入學習

黃水華

(江蘇省江陰市祝塘中學,江蘇江陰，214415)

1 問題呈現

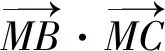
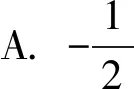
此題以三角形為問題背景，結合三角形的兩邊與夾角的已知條件合理創設情境，通過相應邊上的動點與對應三角形的兩頂點所對應的向量的數量積的構建，來確定對應的最值問題．問題比較常規，難度中等，巧妙設置“動點”，通過動靜結合，“動”中取“靜”，合理求解對應數量積的最值．

2 解題思維

思維視角一：基底思維

方法1：(數量積法)

解析：設MC=t∈[0，3]，

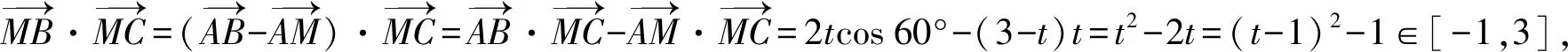
解后反思：隨著線段長度的變化引入對應的參數，結合平面向量的相關知識轉化為含參的二次函數的最值或取值范圍問題，借助配方處理并利用二次函數的圖象與性質來確定數量積的取值范圍．抓住平面向量的基底思維，結合平面向量的線性運算是解決平面向量問題中最常用的基本思維．

思維視角二：幾何思維

方法2：(相交弦定理法)

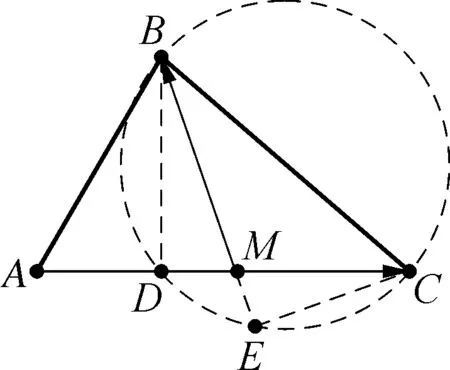
解析：如圖所示，過點B作BD⊥AC，垂足為D，可得AD=ABcos 60°=1，則有DC=2，

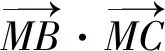
過點C作CE⊥BM，垂足為E，則知B、C、E、D四點共圓，結合圓的相交弦定理，可得MB×ME=MD×MC，

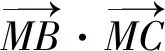
解后反思：根據題目條件合理構建平面幾何圖形，結合所求結論確定動點的位置，通過垂直的構建，結合四點共圓合理構建圓，利用圓的相交弦定理以及平面向量的投影加以轉化與應用，利用基本不等式的應用來確定對應的最值問題．抓住平面向量的幾何思維，利用三角形、圓以及投影等幾何要素來合理轉化與巧妙應用．

方法3：(極化恒等式法)

解析：由AB=2，AC=3，∠BAC=60°，

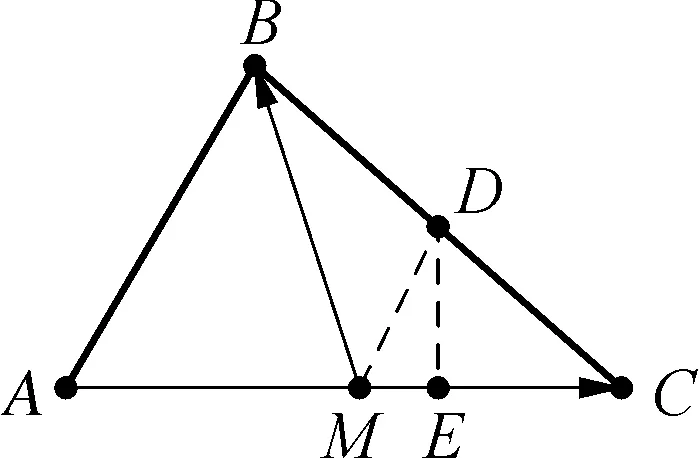
如圖所示，取BC的中點D，連接MD，過點D作DE⊥AC，垂足為E，

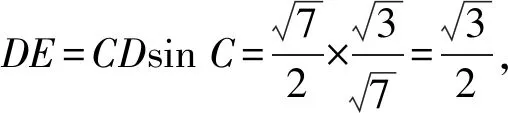
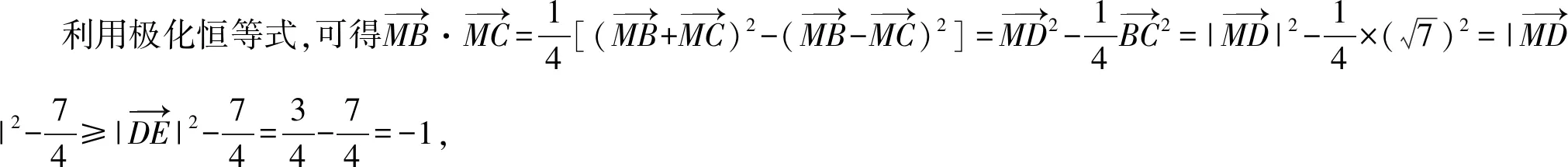
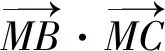
解后反思：根據題目條件加以合理構建平面幾何圖形，借助平面幾何的直觀，通過解三角形思維的應用以及直角三角形的性質特征，利用極化恒等式加以轉化，數形結合來確定對應數量積的最小值，實現問題的直觀轉化與數形結合．抓住平面向量的幾何思維，結合平面幾何圖形的直觀形象來數形結合，合理推理與巧妙應用．

思維視角三：解三角形思維

方法4：(解三角形法)

解析：設MC=t∈[0，3]，

由AB=2，AC=3，∠BAC=60°，

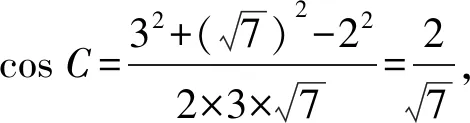
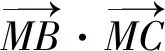
解后反思：隨著線段長度的變化引入對應的參數，結合解三角形中的余弦定理的應用求解對應的邊長與角的余弦值，進而確定對應邊的表達式，綜合余弦定理的向量式加以轉化，構建含參的二次函數的最值或取值范圍問題，結合配方處理并利用二次函數的圖象與性質來確定取值范圍．抓住平面向量的解三角形思維，從三角形視角切入來分析與求解，回歸平面向量相關概念的幾何意義來轉化與應用．

思維視角四：坐標思維

方法5：(坐標法)

解析：以頂點A為坐標原點，AC所在直線為x軸建立平面直角坐標系xAy，

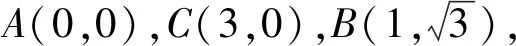
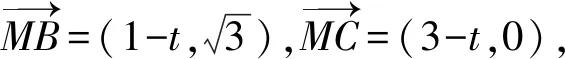
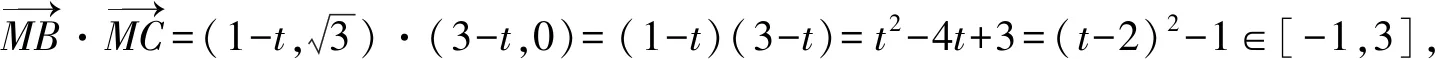
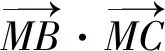
解后反思：將對應的三角形放入平面直角坐標系中去，結合對應點坐標的確定與設置，將幾何問題代數化，借助平面向量的坐標性質與運算加以轉化，進而確定一個含參的二次函數問題，借助配方法的巧妙處理，利用二次函數的圖象與性質來轉化與應用．抓住平面向量的坐標思維，結合平面向量的坐標表示與坐標運算，是代數法解決平面向量問題中一種基本技巧策略．

3 變式拓展

探究1：保持題目條件，改變所求平面向量的數量積的最值為取值范圍，使得問題更加全面，實現問題的進一步拓展與提升．

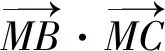
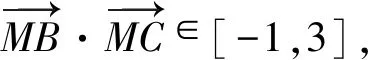
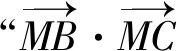
探究2：保持題目條件，進一步加以拓展，求解動點到三角形的三個頂點中任意兩個頂點所對應的向量的數量積之和的取值范圍問題，使得問題變得更加復雜多樣．

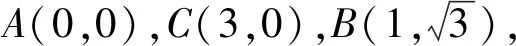
點評：這里也可以設置求解對應平面向量的數量積和式的最小值(或最大值)問題．通過坐標法處理最為合理有效，也是坐標思維的進一步綜合應用．

探究3：在變式2的基礎上，將動點M在規定的邊上運動，拓展到在三角形所在的平面上運動，進而得到以下對應的變式問題．

解析：以頂點A為坐標原點，AC所在直線為x軸建立平面直角坐標系xAy，

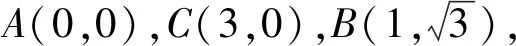
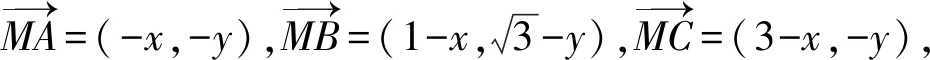
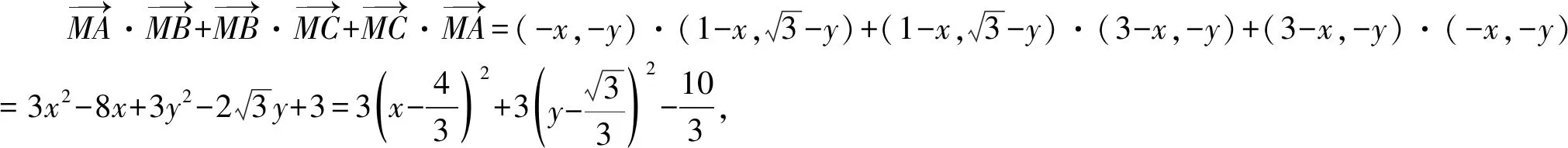
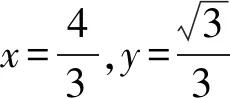
點評：對動點不加以限制.改變其他的限制變化情況，都可以合理創設新的變式問題.解決此問題可以巧妙借助坐標思維加以分析與處理．也可以嘗試其他思維方法.

4 教學啟示

4.1 思維視角總結，方法技巧歸納

解決平面向量時，經常利用基底、幾何與坐標這幾個常見的思維方式進行切入，有時還有解三角形思維、三角函數思維以及特殊思維等，從平面向量的線性運算、坐標運算或三角函數運算等來進行數學運算，或從平面幾何圖象的直觀形象來數形結合，充分展示平面向量同時兼備“數”的性質與“形”的特征這一雙重性質．

4.2 “一題多解”發散，“一題多變”升華

對平面向量問題的“一題多解”，進一步發散思維，融合數學基礎知識與基本技能，形成穩定的知識架構；而借助“一題多變”，進一步升華能力，真正達到會解、會用、會拓展等．在此層面上，進一步實現“一題多得”的良好效果．