伴隨孔對小孔節流氣體靜壓軸承內部氣旋現象的抑制
溫雅茗 連華奇 李育隆 容誠鈞
(北京航空航天大學能源與動力工程學院 北京 102206)
高速、精密、低摩擦的氣體軸承被廣泛應用于計量、超精密機床和半導體等領域[1-3]。但氣體軸承可靠性差、易失穩,容易出現氣錘振動和微幅自激振動的現象[4]。微幅自激振動是一種寬頻振動,其振動幅值在幾納米到幾十納米之間,嚴重制約軸承工作精度的提高[5]。
目前,國內外學者發現氣浮軸承的微幅自激振動現象與軸承壓力腔內部的氣旋現象密切相關。CHEN和HE[6]注意到氣浮支撐節流孔附近氣旋處溫度高于環境溫度,并說明該種現象會引起氣浮支撐的不穩定。LI等[7]運用大渦模擬,通過監測壓力腔截面上不同時刻的壓力波動與氣旋運動規律,得出氣旋的脫落導致軸承內氣體壓力波動并進而導致軸承微幅自激振動。中國工程物理研究院的孔中科[8]觀察壓力腔內部的氣旋區域氣體的流動方向,認為氣旋處氣體的流動會對氣腔壁產生沖擊載荷,誘發氣錘振動,使軸承失穩。龍威等人[9]用氣旋內外壓差代表氣旋強度,并通過改變供氣壓力使氣旋內外壓差Δp增大,當Δp從0.7 kPa增加至1.3 kPa時,氣膜的量綱一振動幅值從0.02增大至0.045。因此,可認為氣旋及其脫落是靜壓氣體軸承產生微振動的原因,氣旋強度越大,軸承的微振動振幅越大。
為了消除氣旋現象,國內外學者進行了大量研究,主要分為改變壓力腔形狀以及改進節流形式兩類。AOYAMA等[10]在壓力腔出口處增加圓角,抑制氣旋產生,增加了氣膜內氣體流動的穩定性。葉燚璽[5]研究了矩形、球形、菱形壓力腔內的氣旋強度,發現球形、菱形壓力腔內的氣旋強度更低。OTSU等[11]在節流孔出口處增加圓周槽狀淺腔,增大了軸承發生失穩的極限轉速。LI等[12]在壓力腔內部增加環形擾流臺,阻擋氣旋沿徑向的移動和發展,顯著降低了軸承氣膜內的壓力波動。改進節流形式方面,CHEN等[13]則將單孔節流改為孔徑等大的多孔陣列式節流,抑制了壓力腔內的氣旋尺度及脫落,減小了軸承的微振動。鄒麒等人[14]采用等直徑小孔環形陣列式節流,通過對比單孔節流軸承與陣列式節流軸承壓力腔內的壓力分布,得出小孔環形陣列節流能夠減小軸承的微振動。張方方[15]采用環形陣列小孔與多孔材料相結合的復合節流形式,進行大渦模擬并得到該種軸承的氣膜內壓力波動最大值為0.803 Pa,說明該種軸承的穩定性遠大于帶壓力腔的單孔節流軸承。在抑制氣旋發展,降低氣旋強度方面,目前的研究主要集中在改進壓力腔結構形式上。在節流方法上,目前學者大多關注采用陣列節流對軸承穩定性的提高,缺乏對軸承壓力腔內部氣旋現象及流動機制的研究。
為了解決壓力腔內大尺度渦結構引起的軸承微振動問題,本文作者從改進軸承節流方式的角度出發,提出了一種具有主進氣孔加伴隨孔復合節流形式的小孔節流氣體軸承,并對其進行仿真計算,重點分析壓力腔內部氣旋現象隨伴隨孔直徑和伴隨孔與主進氣孔間距的變化以及軸承的靜承載特性。
1 數值模型及模擬結果驗證
1.1 數值模型
無伴隨孔小孔節流氣體靜壓止推軸承是一種受到廣泛應用的經典結構,如圖1(a)所示。其結構參數包括:進氣孔直徑d0、進氣孔長度L0、壓力腔直徑d1、壓力腔深度δ、軸承外徑D、氣膜厚度h。取L0=1 mm,d1=1.2 mm,δ=0.2 mm,D=40 mm,h=25 μm。
文中提出了一種帶伴隨孔的復合節流靜壓止推軸承,結構如圖1(b)所示。主進氣孔周圍增加4個直徑小于主進氣孔的伴隨孔,伴隨孔的直徑記為d,伴隨孔長度與主進氣孔相同。其軸線沿周向均勻分布于距主進氣孔軸線一定距離的圓周上,該距離記為L。除新增伴隨孔結構外,該軸承的其他結構參數均與無伴隨孔小孔節流氣體靜壓止推軸承相同。
為研究伴隨孔直徑以及伴隨孔與主進氣孔間距L對軸承承載性能以及壓力腔內部流動的影響,伴隨孔直徑d的變化范圍為0.03~0.15 mm,間距L的范圍為0.35~0.5 mm。
采用結構化網格劃分模型,節流孔處使用O形網格提高網格質量,在軸承主進氣孔與壓力腔交界面、壓力腔與氣膜交界面以及近壁面處進行網格加密。計算網格模型如圖2所示,通過網格無關解驗證得到網格總數在160萬左右。
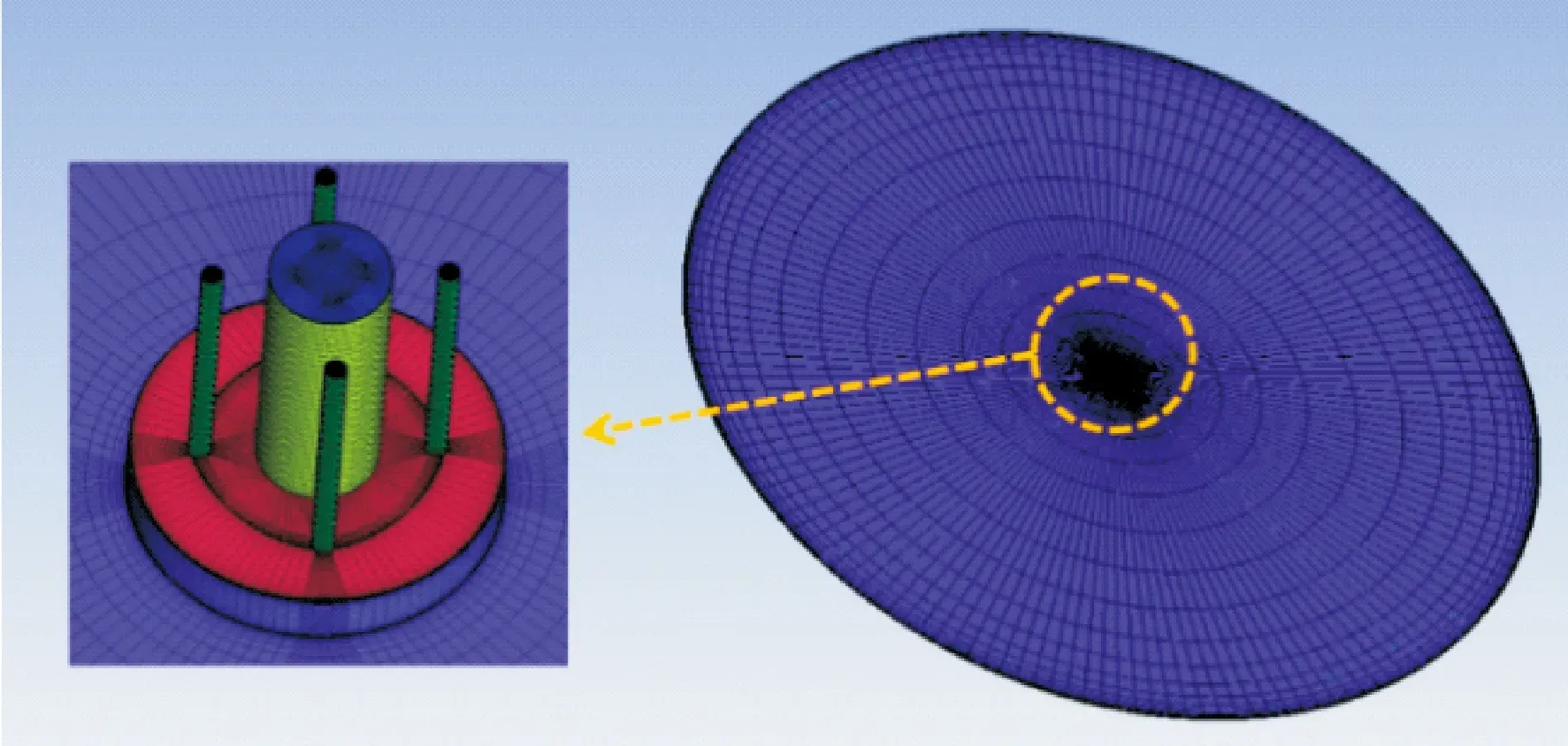
圖2 帶伴隨孔的復合節流靜壓止推軸承網格
采用Fluent進行求解,由于realizablek-ε模型能夠模擬射流撞擊、流動分離和二次流、旋流等復雜流動,同時適用于較為廣泛的流動類型[16],因此文中選取realizablek-ε模型進行計算。
控制方程選用帶能量方程、考慮黏性耗散的三維N-S方程。選用基于壓力的求解器,氣體選取可壓縮理想氣體,氣體常數為一般取值,選用simple算法進行壓力速度耦合計算,采用二階迎風格式以獲得更好的計算精度。全場最大殘差小于10-5時計算結束。設定節流孔進口壓力為5 MPa,溫度為300 K。
1.2 模擬結果驗證
對比文獻[17]中節流孔直徑為0.2 mm,壓力腔直徑為2 mm,壓力腔深度為1 mm的模型,在供氣壓力0.5 MPa,氣膜厚度14 μm條件下仿真分析了沿軸承徑向的壓力分布,并與文獻實驗結果進行對比,如圖3所示。受壓力進口延長段形狀和長度的影響,仿真結果在R=0~1 mm與實驗結果存在一定誤差,但整體能夠較好地反映壓力沿軸承徑向的變化規律,驗證了仿真計算正確性。
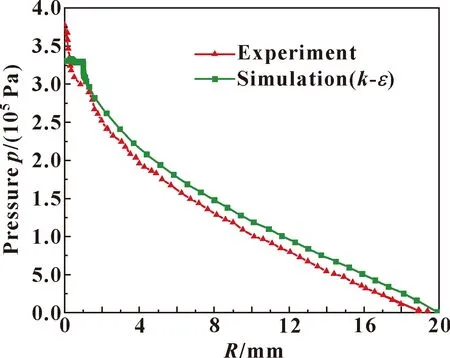
圖3 模擬結果驗證
2 承載特性分析
2.1 承載特性隨伴隨孔直徑的變化
固定軸承氣膜厚度h=25 μm,伴隨孔與主進氣孔間距L=0.375 mm,在0.03~0.15 mm范圍內改變伴隨孔直徑d,得到不同伴隨孔直徑下軸承承載力和出口流量的變化曲線,如圖4所示。
圖4表明,在氣膜厚度相同的條件下,承載力與出口流量呈正相關,總體呈現先下降再上升的趨勢,并在伴隨孔直徑d=0.1 mm時達到最小值。研究中保證進出口壓力一定,相對于無伴隨孔情況,帶伴隨孔的復合節流靜壓止推軸承進口面積更大但總出口流量卻更小,這是由于伴隨孔流量對主進氣孔流量存在抵消作用,而在d=0.1 mm工況下伴隨孔流量對主進氣孔流量的抵消作用最為明顯,該現象在下文的流場圖中也能體現。在伴隨孔直徑d<0.1 mm時,承載力持續下降,這時通過伴隨孔引入的流量不僅不能起到有效的承載作用,反而會破壞軸承內部原有的流動,導致承載能力下降。伴隨孔直徑d>0.1 mm后,承載力和出口流量呈上升趨勢。這是由于隨著伴隨孔直徑的增大,引入流量越來越多,這部分流量的承載作用相對其對于流場的擾動逐漸起到主導作用。
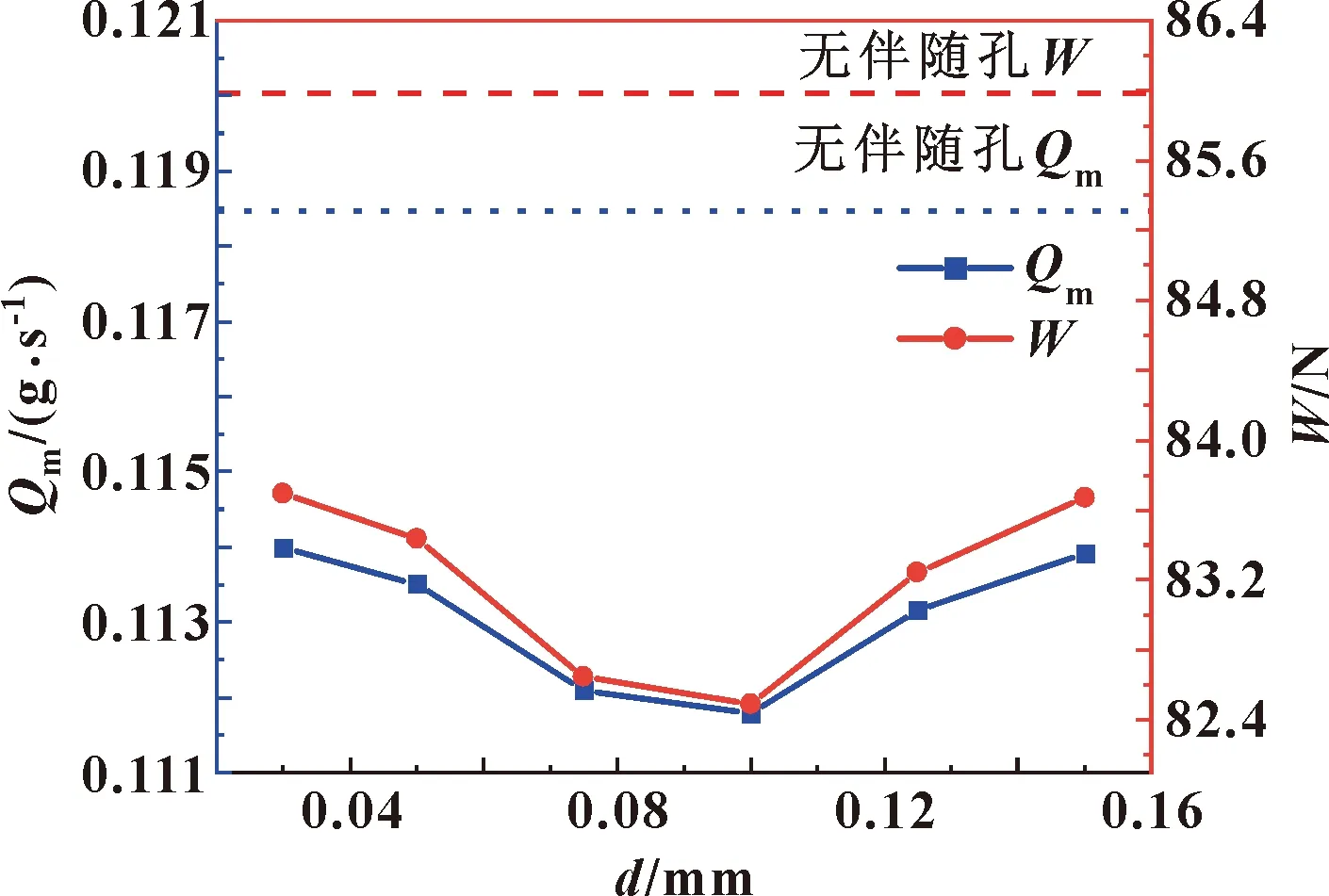
圖4 伴隨孔直徑對出口流量和承載力的影響
對比無伴隨孔小孔節流氣體靜壓止推軸承的承載特性,在主進氣孔周圍添加伴隨孔會引起軸承承載力和出口流量小幅下降,最大降幅分別為5.6%和4%。
2.2 承載特性隨伴隨孔與主進氣孔間距的變化
固定氣膜厚度h=25 μm,伴隨孔直徑d=0.075 mm,在0.35~0.5 mm范圍內改變伴隨孔中心與主進氣孔中心之間的距離L,得到不同孔徑下帶伴隨孔的復合節流靜壓止推軸承的承載力和出口流量的變化曲線如圖5所示。可以看出,軸承的承載力與流量正相關,兩者的變化規律近似相同。
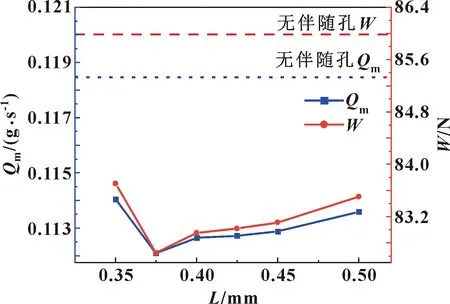
圖5 伴隨孔與主進氣孔間距對出口流量和承載力的影響
在伴隨孔與主進氣孔軸線間距L從0.35 mm增至0.375 mm過程中,流量和承載力下降并在L=0.375 mm處達到最小值;當L>0.375 mm時,流量和承載力隨L的增大而緩慢增大。這同樣是因為,在L=0.375 mm時,伴隨孔流量對主流流量的抵消L=0.375 mm作用最為明顯,因此總流量出現極小值,該現象在下文的流場圖中也能體現。不同伴隨孔與主進氣孔間距下,帶伴隨孔的復合節流靜壓止推軸承的出口流量和承載力相比于無伴隨孔情況最多分別減小了5.30%和3.70%。
3 流場分析
3.1 渦識別方法介紹
采用LIU等[18]提出的Ω渦識別方法對壓力腔內流場渦的強度進行判定,Ω的定義如下:
(1)
其中:
(2)
B=
(3)
ε=0.002Qmax
(4)
作為第三代渦識別方法,Ω方法的物理意義比Q、λ2、Δ和λci等第二代渦識別方法[19-22]更為清晰。Ω為旋轉部分渦量大小占總渦量大小的比例,顯然0≤Ω≤1,可以將其理解為渦量的濃度或渦的相對強度[23]。在該方法下,渦結構對Ω值的變化不敏感,通常取Ω=0.52~0.63顯示渦結構。ε為使分母不為0而引入的小的正數,由經驗公式(4)確定[24],其中Qmax為第二代渦識別方法Q方法在流場中的最大計算值。為保證最佳顯示效果以及便于分析,文中所有算例取ε=9×10-11,取Ω=0.52。
3.2 變伴隨孔直徑對流場的影響
固定軸承氣膜厚度h=25 μm,伴隨孔與主進氣孔間距L=0.375 mm,在0.03~0.15 mm范圍內改變伴隨孔直徑d,得到不同孔徑下的壓力腔對稱面內的Ω分布云圖如圖6所示。
由圖6(a)可以看出,在無伴隨孔的情況下,壓力腔內存在明顯的氣旋現象,該氣旋結構飽滿,幾乎占據整個壓力腔;在靠近氣旋的中心位置渦的相對強度最大,Ω接近于1。在添加伴隨孔后,該氣旋被引入的氣流分成了左右兩部分,并且每部分的強度相對于無伴隨孔的情況均有減小。流體沖擊至承載面上后,其流動方向發生改變。在伴隨孔與主進氣孔之間區域,伴隨孔流量的流動方向與主進氣孔流量流動方向相反,在對沖作用下產生了2個腎狀渦。同時,伴隨孔流量抵消了部分主流流量,造成軸承總出口流量減小。由圖6(b)可知,當d=0.03 mm時,由于從伴隨孔引入的流量過小,不能有效減小渦的強度,此時伴隨孔右側的旋渦強度仍然很大,旋渦中心存在著明顯的高Ω區域。由圖6(c)可知,當d=0.05 mm時,旋渦中心的高Ω區域的區域減小,渦的強度有所降低,但是整個旋渦結構仍然相當清晰。隨著直徑的繼續增大,當d=0.075 mm時,流場中右側旋渦結構開始被破壞,高Ω區域的范圍進一步縮小(見圖6(d)),可以認為此時壓力腔內的氣旋得到了明顯的抑制。如圖6(e)—(g)所示,在伴隨孔直徑d≥0.1 mm后,伴隨孔右側流場中的渦結構幾乎完全消失,隨著伴隨孔直徑的增大,流線也更加平直。當d=0.125 mm時,壓力腔內左右兩部分旋渦的尺度同時達到最小,強度最低。
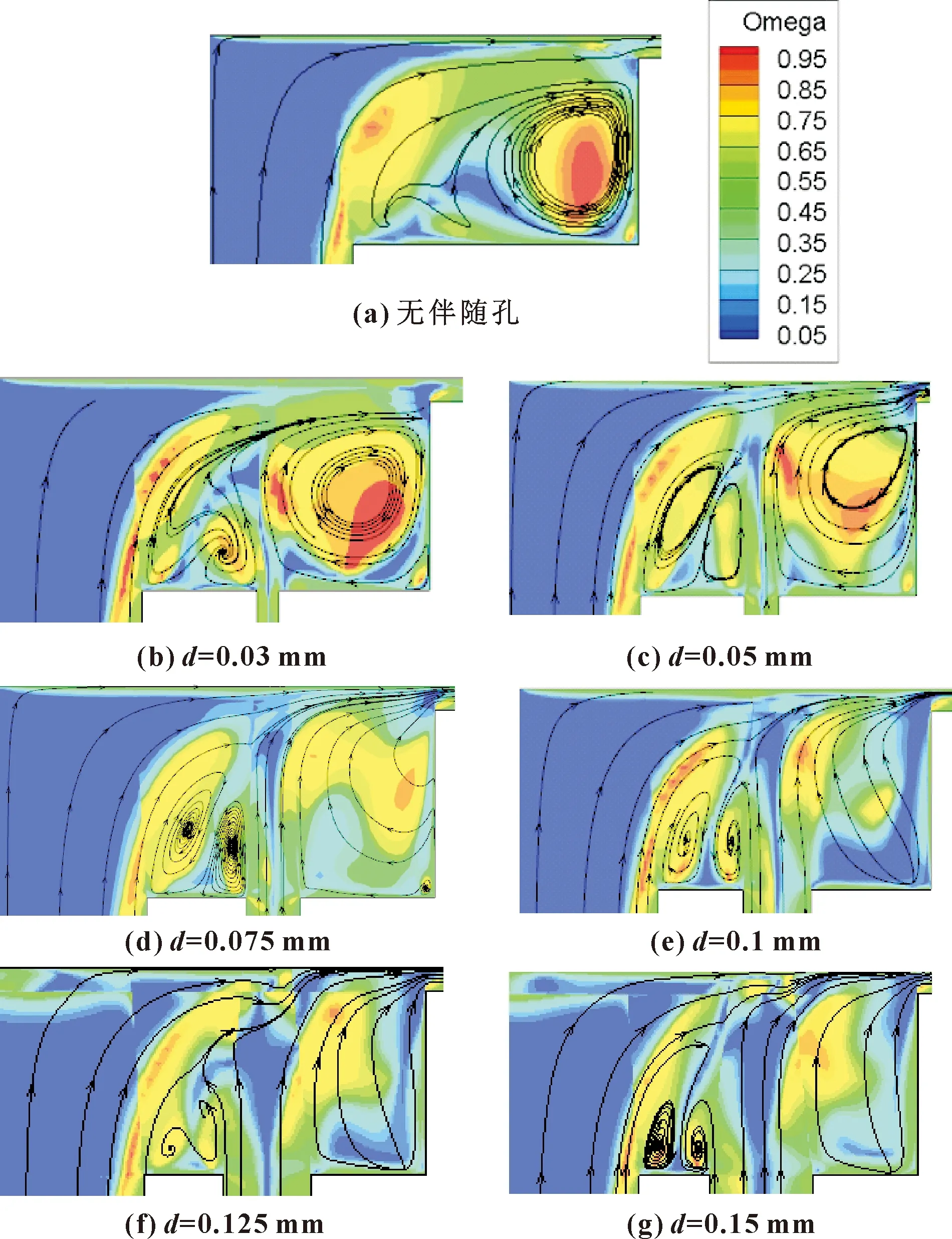
圖6 不同伴隨孔直徑時壓力腔對稱面Ω分布
綜合以上分析可知,采用帶伴隨孔的復合節流方式對壓力腔內的渦結構的發展有明顯的抑制作用,能夠減小氣旋尺度,增加軸承的穩定性。
由于氣旋區域的流體微團是繞氣旋中心轉動的,微團所受的離心力與流場內的壓力差相平衡,因此氣旋邊緣的壓力高,中心的壓力低。氣旋越強,氣旋周圍區域流體微團的運動速度越快,所受的離心力越大,因而氣旋內外的壓力差越大。氣旋所在區域往往形成一個低壓區。
下面通過氣旋中心與邊緣的壓差Δp來進一步定量說明氣旋存在處的流場壓力降低的強度。以Ω=0.52識別出氣旋邊界,提取出氣旋表面的壓力值并與流線匯聚處的壓力做差,即可得到邊緣與中心壓差如圖7所示。
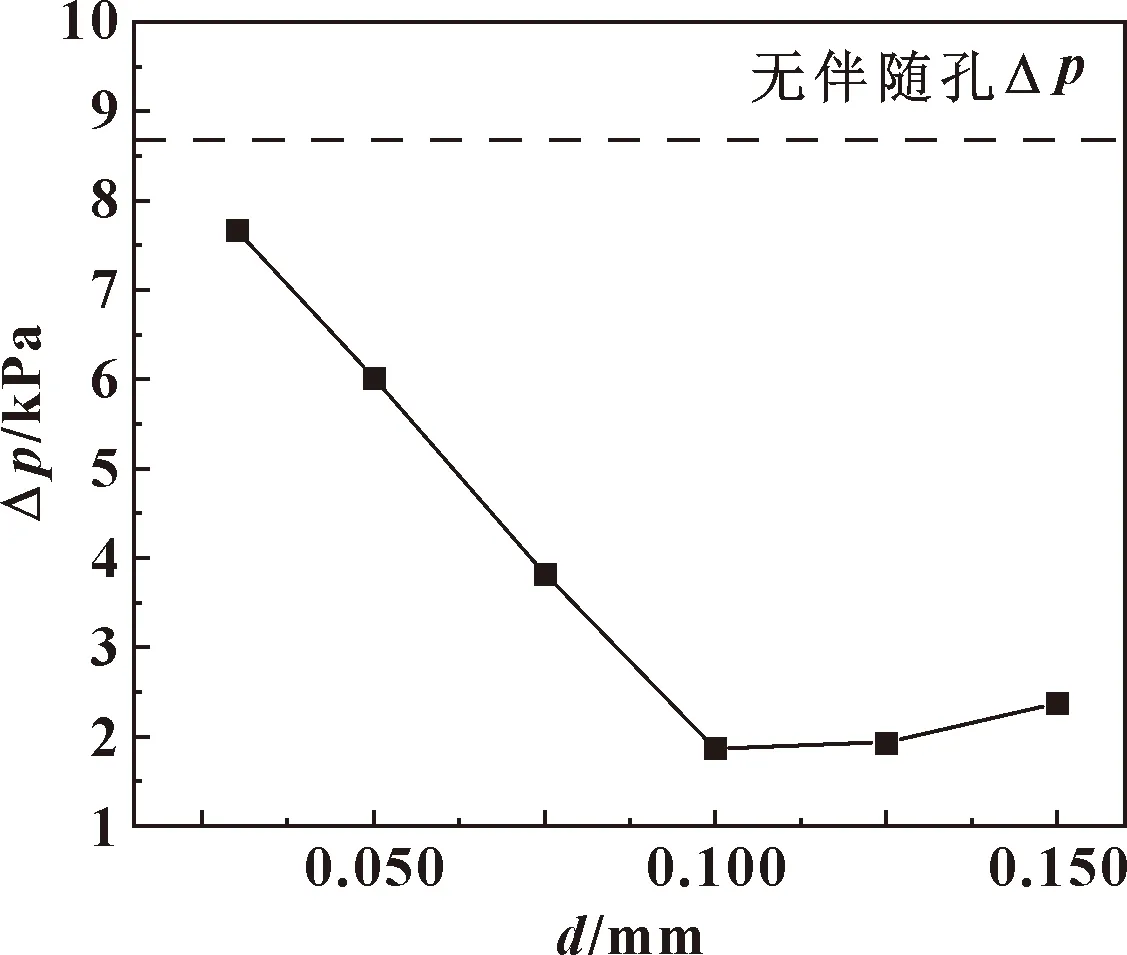
圖7 伴隨孔直徑對氣旋現象的影響
無伴隨孔小孔節流氣體靜壓止推軸承的氣旋內外壓差約為8.6 kPa,加伴隨孔后止推軸承的氣旋內外壓差均較無伴隨孔時明顯減小,其中伴隨孔直徑d=0.1 mm情況下氣旋內外壓差最小,相比與無伴隨孔時,氣旋內外壓差減少了78%。
3.3 變伴隨孔與主進氣孔間距對流場的影響
固定氣膜厚度h=25 μm,伴隨孔直徑d=0.075 mm,在0.35~0.5 mm范圍內改變伴隨孔中心與主進氣孔中心之間的距離L,得到壓力腔對稱面內的Ω分布云圖,如圖8所示。可以看出,添加伴隨孔后,壓力腔右側的高Ω值區域明顯縮小,壓力腔內的旋渦強度有顯著下降。隨著L的不斷增大,伴隨節流孔與壓力腔壁面間的渦結構基本消失,而伴隨孔與主流間的旋渦尺度卻不斷增大。L在0.35~0.375 mm范圍內時,伴隨節流孔與主流間旋渦的尺度較小,這是由于主進氣孔和伴隨孔軸線之間的間距較小,旋渦的發展空間有限。當L=0.375 mm時,伴隨孔與主進氣孔間位置處的兩腎狀渦的尺寸幾乎相當,對沖作用最強,故此時伴隨孔流量對主進氣孔流量的抵消作用最強,氣體軸承的總出口流量最小。當L>0.35 mm時,伴隨節流孔與主流間旋渦的尺寸明顯增大,強度增強,這是由于L的增大給旋渦提供了更大的發展空間。
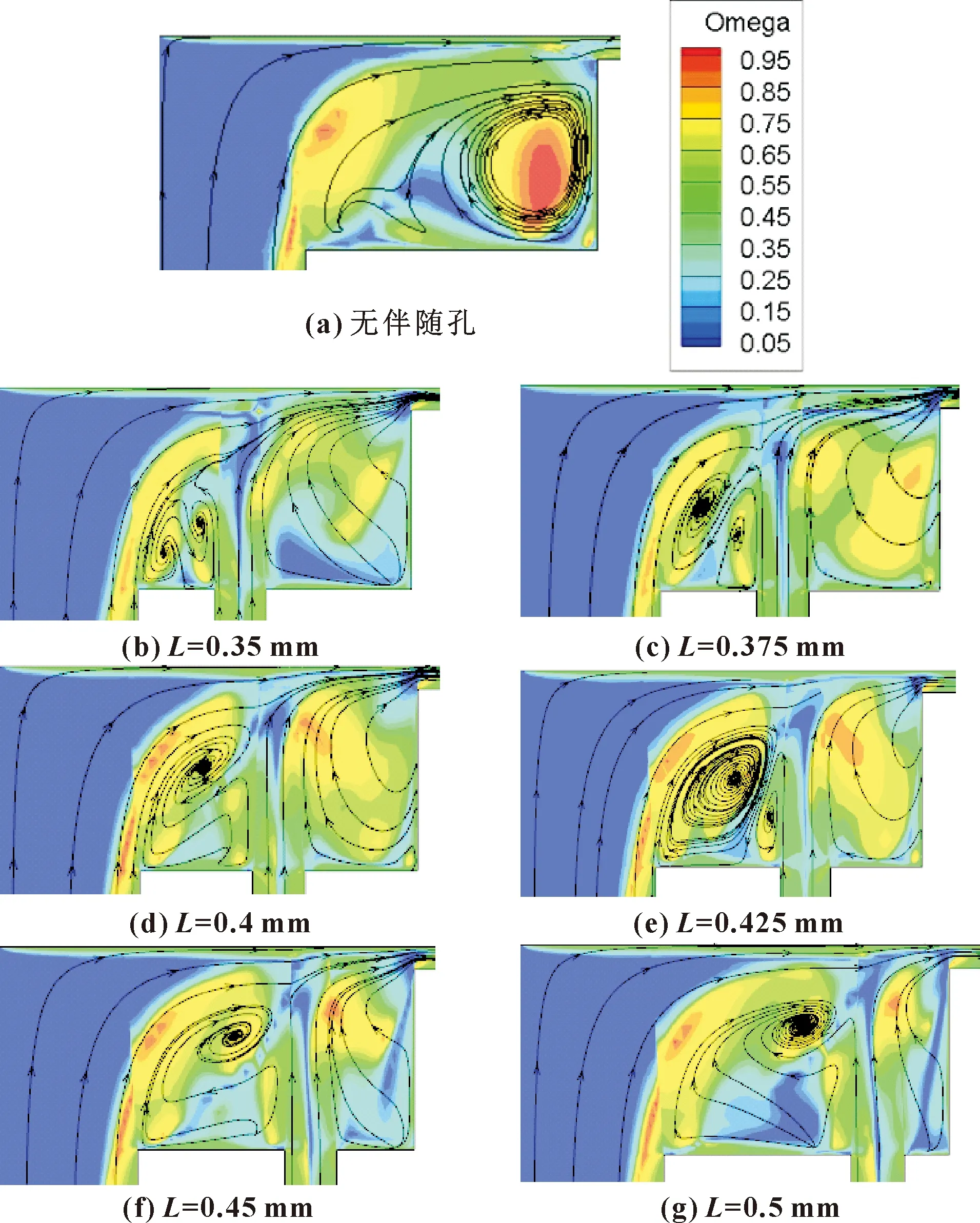
圖8 不同伴隨孔與主進氣孔間距下壓力腔對稱面Ω分布
下面通過氣旋中心與邊緣的壓差來進一步定量說明氣旋存在處的流場壓降的大小。旋渦內外壓差的變化曲線如圖9所示。旋渦內外壓差的變化曲線顯示的規律與云圖結果基本一致,總體呈現隨伴隨孔與主進氣孔間距增大而增大的趨勢。在L=0.35 mm時旋渦內外壓差最小,相比于無伴隨孔工況,氣旋內外壓差減少了71%。
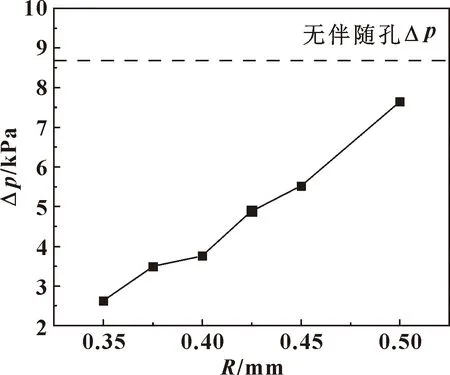
圖9 伴隨孔與主進氣孔間距對氣旋現象的影響
4 結論
(1)采用主進氣孔與伴隨孔復合節流的節流方式能有效抑制壓力腔內部的氣旋現象,相對渦強度明顯降低,氣旋內外壓差最大減小78%。
(2)采用主進氣孔與增加伴隨孔復合節流的節流方式會使承載力和出口流量小幅下降。隨伴隨孔直徑和伴隨孔與主進氣孔間距的增大,承載力與出口流量總體呈現先下降再上升的趨勢;在軸承氣膜厚度h=25 μm,伴隨孔與主進氣孔間距L=0.075 mm條件下,當d=0.1 mm時承載力與出口流量最小,降幅分別為5.6%和4%;在軸承氣膜厚度h=25 μm,伴隨孔d=0.075 mm條件下,當L=0.375 mm時,承載力和出口流量最小,降幅分別為5.3%和3.7%。
(3)固定其他條件不變,隨伴隨孔直徑的增大,軸承壓力腔內氣旋受到的抑制效果先增強后減弱;當伴隨孔直徑d<0.1 mm時,軸承壓力腔內氣旋受到的抑制效果隨d的增大而增強,當d≥0.1 mm時,氣旋的強度雖略有增加但仍處于較低水平;固定其他條件不變,隨著小孔與主孔距離的增大,對氣體旋的抑制作用不斷減弱,當L=0.35 mm時軸承壓力腔內氣旋受到的抑制效果最佳。

