前視成像中Keystone 變換殘余距離走動的頻域補償

李澤森 李悅麗 張金福

（國防科技大學電子科學學院,長沙 410073）

引 言

雷達具有全天候、全天時、遠距離的目標探測和定位能力，前視成像是指在飛行過程中雷達天線對前視方向進行扇形掃描并結合超分辨或單脈沖測角技術來提高前視方向的方位分辨率[1-2]，具有系統復雜度低、對航跡無特殊要求、方位分辨率改善顯著等優點.

對空載雷達前視成像而言，平臺高速運動會導致目標積累時間內出現嚴重的距離走動現象，影響圖像聚焦性能，因此需要對目標跨距離單元走動進行校正.Keystone 變換是一種有效校正目標線性距離走動的方法，最早由Perry 等人提出[3]并應用于合成孔徑雷達[4-6]，張順生等人將Keystone 變換引入到雷達微弱目標的長時間積累領域[7]，也取得了良好的積累效果.Keystone 變換具有以下優勢：1)可同時對多個目標進行線性距離走動補償；2)保留了目標回波的相位信息，便于實現相參積累；3)在較低信噪比時依舊適用.Keystone 變換因其優越的性能，又被廣泛應用于運動平臺前視成像中[8-10].

雷達脈沖重復頻率(pulse repetition frequency,PRF)限定了可觀測到的最高多普勒頻率，當運動平臺速度較高或者雷達采用低PRF 時，將發生多普勒模糊，此時直接觀測得到的多普勒譜的峰值頻率點不再為多普勒中心的真實值，必須進行解多普勒模糊[11].常用的解多普勒模糊方法有一維集算法、中國余數定理法等[12].相關研究對多普勒模糊數的影響進行了分析[13-14]，但沒有考慮模糊數與真實多普勒中心誤差的影響.在運動平臺前視成像模型中，平臺飛行速度屬于先驗信息，易獲得多普勒模糊數，但在解多普勒模糊時，采用Keystone 變換校正的模糊數補償可能引入速度殘差，導致目標定位誤差.現有解決方法通常選取平臺飛行速度對應的特定PRF，盡可能降低引入的速度殘差[10,15]，但并未深入討論解模糊所導致的速度殘差問題.

本文首先研究了在多普勒模糊的情況下，基于Keystone 變換進行前視成像距離走動校正可能產生的速度殘差問題，推導提出一種頻域補償Keystone變換殘余距離走動的方法.該方法可以消除Keystone變換所產生的速度殘差，通過理論分析與仿真實驗驗證了所提出方法的有效性.

1 前視成像距離走動誤差影響分析和補償方法

1.1 運動平臺前視成像幾何模型

前視高分辨成像通常是指雷達對前視方向采用掃描模式進行連續掃描，然后通過沿距離門的超分辨或單脈沖測角技術改善前視實孔徑雷達圖像方位分辨率的方法[2,10].

但是，由于雷達平臺的運動，目標在回波距離門上的位置會發生變化，如圖1 所示.機載雷達以勻速v從A點飛到B點的過程中，目標點P相對雷達的瞬時斜距為

圖1 運動平臺前視成像幾何關系模型Fig.1 Geometric model for forward-looking imaging of moving platforms

式中：R0為A點雷達平臺到目標P的瞬時斜距；tm為慢時間；θ為目標相對飛行軌跡所在坐標軸Y軸的斜視角；φ為雷達對目標的俯視角.對式(1)進行泰勒級數展開，可以得到

在雷達天線波束掃描過程中，由于平臺的前向飛行速度，回波中目標相對天線相位中心的距離會發生變化，式(2)中第2 項表示由前向飛行速度引起的線性項，稱為距離走動，其值與 θ 和φ均有關.在遠場成像時φ的變化相對較小，可以認為φ角相對固定，忽略其變化.在天線掃描成像的過程中，不同方位相同距離的目標回波會在同一時刻到達，但是它們在不同幀之間的距離走動各不相同，使得無法進行統一的校正.對這種空變距離走動進行補償的方法有兩種：頻域距離走動校正或Keystone 校正.

1.2 頻域距離走動校正

假設雷達發射線性調頻脈沖信號，雷達發射信號的時域表達式為

式中：δ(t)為 chirp 脈沖；m為脈沖序列；Tr為脈沖重復時間；fc為載波中心頻率.

雷達接收到距離壓縮后的時域回波可以表示為

式中：A為點目標的回波強度；p(·)為歸一化的回波包絡；=t-tm為快時間；tm=mTr.將式(4)沿快時間維t?做傅里葉變換，得到回波在距離頻域表達式為

式中：P(fr)為p()的傅里葉變換；fr為快時間t?的頻域.

式(2)中 θ角的變化范圍為前視方向目標區域成像角度范圍，通常小于15°，對應余弦值變化很小，因此在距離走動校正時可以忽略不同 θ角目標的距離走動差異，統一用正前方目標的距離走動曲線進行校正，此時式(2)可化簡為

式(7)中，指數項第二部分表明距離頻率與多普勒頻率之間存在耦合關系，文獻[16]中針對跨距離單元走動提出了一種頻域距離走動校正方法，該方法通過共軛消除距離頻率與多普勒頻率之間的耦合.

采用頻域距離走動校正的方法對式(5)中的回波包絡進行校正，消除距離頻率與多普勒頻率的耦合項，可以得到

由式(9)可以發現，頻域距離走動校正方法將會引入殘余包絡誤差 ΔR(tm)：

前視成像區域內 θ角較小，ΔR(tm)主要由第一項組成，且在速度較小時，式(10)中第一項接近于零，此時殘余包絡誤差可以忽略.但是當速度較大時，殘余包絡誤差急劇增大，所以此時采用頻域距離走動校正方法時將會引入較大誤差.為解決這一問題，前視成像通常采用Keystone 變換進行距離走動校正.

1.3 Keystone 校正方法和問題分析

令R(tm)=R0-vtmcos θcosφ，帶入式(5)中得

為消除距離頻率與多普勒頻率之間的耦合，對慢時間進行尺度伸縮變換，令

即Keystone 變換[3]，得到

Keystone 變換消除了距離頻率與多普勒頻率之間的耦合，補償了目標的線性走動.對高波段雷達，通常滿足fr?fc，式(13)滿足fc/(fc+fr)≈1，且指數項第二項與距離頻率無關.對式(13)進行傅里葉反變換得到

由式(14)可以看出，經過Keystone 變換距離走動校正后，目標在不同方位的位置均為R0，說明Keystone變換消除了距離頻率與多普勒頻率之間的耦合，補償了目標的距離走動.

實際上，雷達是以慢時間tm進行采樣的，fc/(fc+fr)×時刻并沒有實際的采樣值，通常需要采用sinc 內插算法實現Keystone 變換[17].

對于高波段雷達，由于PRF 小于多普勒中心頻率往往引起多普勒模糊問題，所以在進行sinc 插值的同時還應進行解多普勒模糊相位修正.在多普勒模糊的情況下，Keystone 變換實現方法[18]可以表示為

式中：F為多普勒模糊倍數；N為相參積累時間內脈沖個數.

由式(15)可以看出，對模糊數的依賴是Keystone算法的一個限制條件[7]，定義模糊數F為

式中：FR表示PRF；fdc表示多普勒中心頻率，

發生多普勒模糊時實際測得的多普勒中心頻率為fdn，fdw為多普勒帶寬，且有

式中，θ3為3 dB 波束寬度.

圖2 為前視掃描雷達解多普勒模糊產生速度殘差示意圖.當斜視角θ=0°、頻率為fc時，雷達回波的多普勒中心頻率為

天線主瓣內回波的多普勒帶寬為

發生多普勒模糊時測得的多普勒中心頻率為fdn0，多普勒模糊數對應的多普勒中心頻率為

式中：v′=v+Δv為對應的速度，Δv為模糊數補償后相比于真實速度引入的速度殘差，

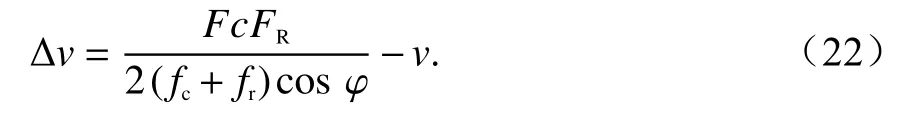
當斜視角 θ ≠0 °、頻率為fc時，所對應的多普勒中心頻率、多普勒帶寬、發生多普勒模糊時測得的多普勒中心頻率以及多普勒模糊數對應的多普勒中心分別為fdcθ、fdwθ、fdnθ、.由圖2 可見，當雷達斜視角增大時，多普勒中心頻率偏移減小，多普勒帶寬增大.因此在正前視方向，利用多普勒帶寬區分目標非常困難，同樣由于飛行方向左右兩側的斜視角都會引起相同多普勒中心偏移，多普勒波束銳化技術存在左右模糊問題.

當fdn0≠0時，因為多普勒模糊數F為整數，用式(15)解多普勒模糊將產生模糊數誤差，且有

如圖2 所示.

圖2 解多普勒模糊產生速度殘差示意圖Fig.2 Schematic diagram of the residual velocity generated by solving Doppler ambiguity

相關研究對多普勒模糊數的影響進行了分析[13-14]，但未考慮模糊數誤差的影響，多普勒模糊情況下所產生的殘余距離走動校正誤差是由于解多普勒模糊時產生了速度殘差.針對產生的速度殘差進行分析，在未發生多普勒模糊時，式(11)中存在距離頻率與多普勒頻率耦合的相位項為

解多普勒模糊后，相位項變為

式(27)說明，經過Keystone 變換校正后，如果模糊數對應的多普勒中心頻率與實際多普勒中心頻率不同，則會引入速度殘差 Δv，將影響最終的目標定位結果.

2 頻域補償Keystone 變換殘余距離走動校正的方法

根據前文的分析，單純采用平臺飛行方向的速度作為參考速度進行頻域距離走動校正，會導致與角度相關的殘余包絡誤差，且這一誤差隨掃描角度增大而增大，在高速平臺上尤其明顯；而采用Keystone變換校正時，由于存在多普勒模糊，解多普勒模糊時可能會產生速度殘差，也會導致空變的目標定位誤差.本節提出一種頻域補償Keystone 變換殘余距離走動的方法，可以消除解多普勒模糊相位修正時所產生的速度殘差，實現目標距離向準確定位.

存在多普勒模糊的情況下，由式(11)與式(27)可以得到經過Keystone 變換后的回波頻域為

雖然距離頻率與多普勒頻率的耦合經過Keystone變換后得到消除，但引入了第二個指數項中距離頻率與速度殘差的耦合.

采用1.2 節中的頻域距離走動校正方法，對式(28)中的速度殘差進行校正：

Keystone 變換的結果經過頻域距離走動校正，消除了速度殘差與距離頻率之間的耦合.同時相比于直接用頻域距離走動校正方法，此時的速度殘差Δv遠小于平臺飛行速度v，殘余包絡誤差 ΔR′(tm)為

對比式(10)，頻域補償時所引入的殘余包絡誤差大大降低.

經過上述處理，最終頻域補償Keystone 變換距離走動校正方法可表示為

頻域補償Keystone 變換距離走動校正方法步驟如下：

1) 將距離壓縮后的雷達回波沿快時間維進行傅里葉變換；

2) 對慢時間進行尺度伸縮變換消除距離頻率與多普勒頻率之間的耦合；

3) 存在多普勒模糊時進行相位修正解多普勒模糊，同時使用sinc 插值方法實現Keystone 變換；

4) 用頻域距離走動校正方法補償Keystone 變換所引入的速度殘差.

3 仿真驗證

3.1 點目標仿真實驗

為驗證所提方法，采用單脈沖前視成像算法進行仿真實驗，仿真所用雷達系統參數如表1 所示.雷達放置在機載平臺上，平臺勻速飛行，發射信號中心頻率fc為18 GHz，脈寬為1 μs，帶寬為50 MHz.雷達掃描范圍為-15°～15°，PRF=2 600 Hz，在地面上以[0，1 700] m 為中心設置3×21 點方陣，目標點的強度為1，點之間方位向、距離向間隔均為30 m.方位向測角采用調頻Z變換重建和差多普勒估計并進行比幅測角的方法[15].

表1 前視掃描成像仿真實驗參數Tab.1 Simulation experimental parameters for forwardlooking scanning imaging

當PRF=2 600 Hz時，設置不同的平臺飛行速度v，分別求出fdc=2v fccosφ/c，多普勒模糊數(其中 〈·〉 表示四舍五入取整)，Δv=(ΔFcFR)/(2fccosφ)，具體參數取值如表2 所示.

表2 平臺不同飛行速度產生的速度殘差Tab.2 Residual velocity by different speeds of the platform

圖3 所示為平臺不同飛行速度下傳統Keystone變換校正結果與頻域補償Keystone 變換校正結果對比.圖3 (a)、(b)、(c)所示為Keystone 變換方法校正結果，由于引入了速度殘差 Δv，導致距離走動校正結果發生偏移. Δv越大，偏移越明顯，Δv的正負導致了不同的偏移方向，Δv為正時產生順時針偏移，Δv為負時產生逆時針偏移.圖3 (d)、(e)、(f)所示為相同參數下采用頻域補償Keystone 變換校正結果，可見所提出的頻域校正方法消除了速度殘差引起的距離誤差，實現了目標準確的距離向定位.

從圖3 (a)與圖3 (d)中分別截取方位向為-300 m的三個目標點繪制歸一化剖面圖，結果如圖4 所示.三個目標點的真實距離分別為1 670 m、1 700 m、1 730 m.可以看出：傳統Keystone 變換校正的三個目標點在距離向均產生了3 m 的偏移；而頻域補償Keystone 變換由于消除了速度殘差引起的距離誤差，實現了距離向的準確定位.

圖3 傳統Keystone 變換與頻域補償Keystone 變換校正結果對比Fig.3 Comparison of the correction results of Keystone transform and the modified Keystone transform

圖4 v=250 m/s 時方位向-300 m 目標歸一化剖面圖Fig.4 Normalized profiles of the targets with an azimuth of-300 m,v=250 m/s

圖5 所示為頻域校正方法與頻域補償Keystone變換校正方法結果對比，設置平臺飛行速度v=270 m/s.截取方位向分別為-300 m、-270 m、-240 m，距離向分別為1 670 m、1 700 m、1 730 m 的3×3 點方陣做等高線圖.可以看出：在機載平臺高速運動時，頻域校正方法產生的殘余包絡誤差較大，導致聚焦效果變差；而頻域補償Keystone 變換方法，僅用頻域校正方法處理速度殘差 Δv，產生的殘余包絡誤差較小，具有更好的聚焦效果.

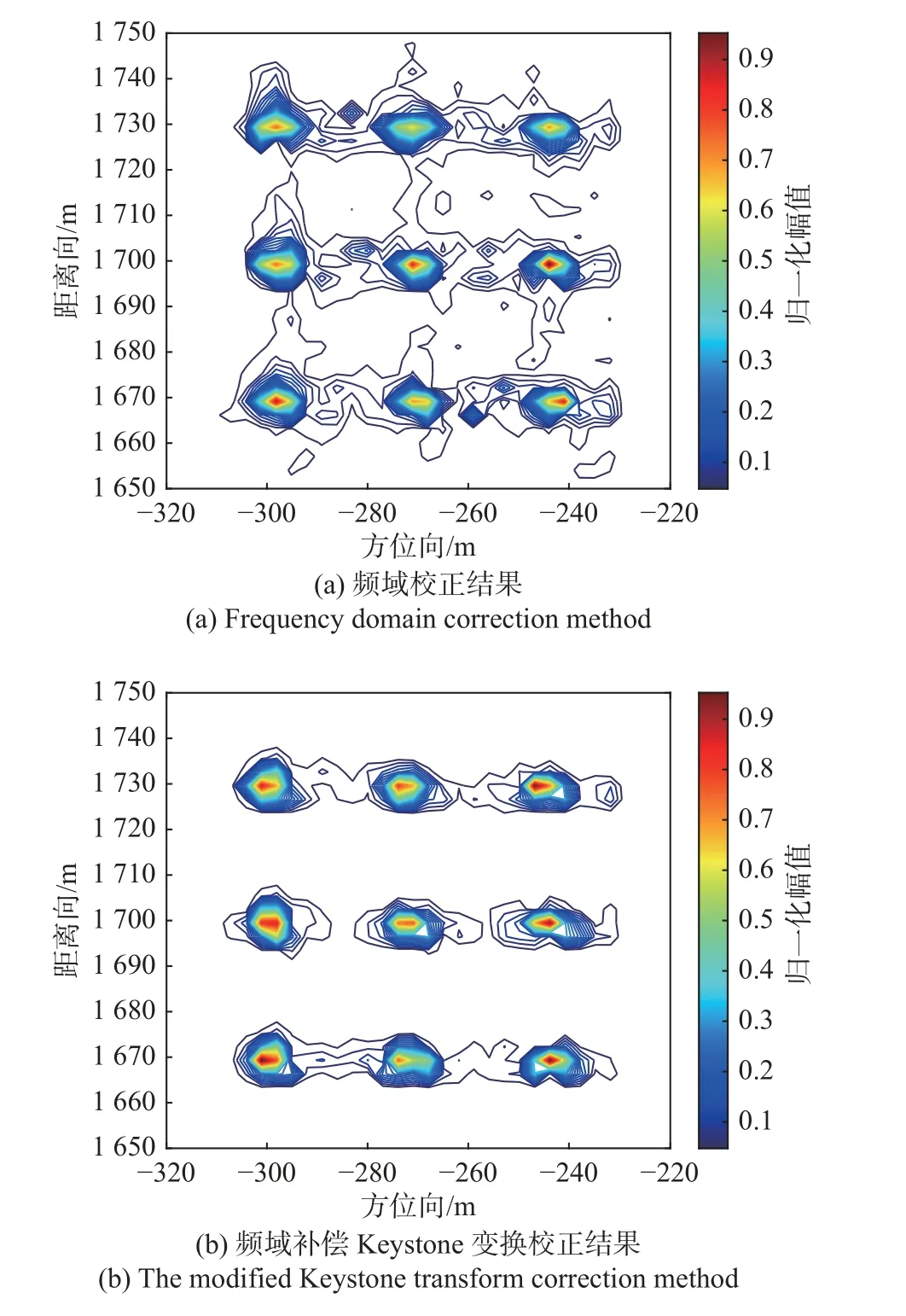
圖5 頻域校正方法與頻域補償Keystone變換校正方法結果對比Fig.5 Comparison of the correction results of frequency domain correction and the modified Keystone transform

為進一步證明所提算法的有效性，分別計算距離向1 700 m，方位向-300 m、-270 m、-240 m 處目標采用頻域校正方法與頻域補償Keystone 變換校正方法校正結果5 倍插值后的距離向積分旁瓣比(integral sidelobe ratio,ISLR)，

式中：Ptotal為總功率；Pmain為主瓣功率，主瓣寬度以峰值為中心，大小取兩倍3 dB 帶寬.兩種方法距離向ISLR 結果如表3 所示，圖6 所示為距離向1 700 m、方位向-300 m 的目標5 倍插值后的距離向剖面圖.在同一方位向處，頻域補償Keystone 變換校正方法的距離向ISLR 均低于頻域校正方法的距離向ISLR，說明頻域補償Keystone 變換校正方法能量更集中，聚焦效果更好.同時，頻域校正方法的距離向ISLR 隨著方位向的降低而減小，這是因為隨著斜視角 θ的減小，式(10)所示的殘余包絡誤差變小，聚焦效果變好.

表3 頻域校正方法與頻域補償Keystone 變換校正方法的距離向ISLR 對比Tab.3 ISLR comparison between frequency domain correction method and the modified Keystone transform

圖6 距離向1 700 m、方位向-300 m 的目標距離向剖面圖Fig.6 Target distance direction profiles with a distance of 1 700 m and azimuth of -300 m

3.2 場景仿真實驗

點目標仿真實驗驗證了頻域補償Keystone 變換方法的有效性，接下來驗證所提出方法用于重建擴展目標的可行性.仿真采用一幅Ku 波段的SAR 圖像作為原始場景，對圖像進行降采樣處理，圖像分辨率為3 m×3 m，如圖7 (a)所示.圖像數據置于以[0，1 700] m 為中心的地面，平臺飛行速度為100 m/s，其余參數與表1 中相同，成像結果用dB 圖表示.

圖7 仿真場景校正結果對比Fig.7 Comparison of correction results in simulation scenes

圖7 (b)與圖7 (c)分別為傳統Keystone 變換方法與頻域補償Keystone 變換方法成像結果，紅色虛線為目標真實場景位置.傳統Keystone 變換方法校正結果產生了偏移而頻域補償Keystone 變換方法可以準確地重建目標場景.實驗結果驗證了頻域補償Keystone 變換方法重建擴展目標時的有效性.

4 結 論

機載運動平臺雷達前視掃描成像時，由于運動平臺速度較高，常會引起多普勒模糊.在進行距離走動校正時，使用傳統Keystone 變換方法將引入速度殘差，造成距離走動校正失準.現有解決方法通常選取特定的PRF 與平臺飛行速度，盡可能降低引入的速度殘差，但限制了系統選擇的靈活性.本文首先分析了速度殘差產生的原因，進一步提出了一種頻域補償Keystone 變換殘余距離走動的方法，可適應不同的PRF 與平臺運動速度，該方法可以消除Keystone 變換所引入的速度殘差，實現目標距離向的準確定位，理論分析與仿真實驗驗證了該方法的有效性.如何消除二次包絡誤差，實現更好的聚焦效果，以及實現復雜機動情況下的距離走動校正，這將是我們下一步的研究方向.