可重構力學超材料的設計與波動特性研究1)

肖伯雅 楊 洮 馮亞菲 劉 宇 徐文帥 陳 猛,2) 姜 恒,3)王育人

* (中國科學院力學研究所微重力實驗室,北京 100190)

? (中國科學院大學工程科學學院,北京 100049)

** (中國人民解放軍92228 部隊,北京 100072)

引言

力學超材料由于其超常的物理屬性,如負泊松比[1-2]、剪切模量消隱[3]、負壓縮性[4]、可調剛度[5-7]、輕質高強[8]等,結構往往具備良好的抗變形、耐疲勞或耐高壓能力,在航空航天輕質高強結構[9-10]、隔振吸能結構[11-13]、深海耐壓結構[14-15]等領域有著廣泛的應用.其中具有可調剛度的可重構雙穩態結構可以通過外加力場的方式主動調控整體結構的構型,這一獨特屬性給研究人員提供了極大的設計自由度,大大拓展了功能材料的設計空間,因此近年來雙穩態結構受到科研人員的廣泛關注.

彎曲梁模型作為典型的雙穩態結構于2004 年由Qiu 等[16]提出,利用深反應離子刻蝕(DRIE)制備了微米級的雙穩梁,進行了試驗和仿真計算,其測試結果與仿真結果基本一致.起初雙穩態梁結構主要應用于微機電系統(MEMS),Wu 等[17]利用雙穩態梁結構設計制造出了微懸臂致動器,可以應用于低功率雙穩態繼電器中.Huang 等[18]通過雙穩態梁結構與杠桿結構組成的雙穩態裝置,用來制作微機電系統中具有雙穩性和推入推拉功能的設備.后續科研人員對雙穩態梁結構也進行了力學方面的研究,Yang 等[19]利用熱塑性聚氨酯彈性體橡膠(TPU)成功制備了彎曲梁雙穩態結構,研究了結構幾何參數對整體力學性能的影響.之后Darwish 等[20]將鋼板作為骨架,用尼龍材料制備了彎曲梁可重構結構,研究了多成分材料結構穩態轉變過程中的力學特性.Zhang 等[21]用PLA 材料作為骨架,將0.1 mm 厚的鋼板加工成彎曲梁結構,兩者合成的新型多穩態結構相比于之前的同類結構多了傾斜的穩態構型.Hua 等[22]研究了彎曲梁結構在隔振和吸能方面的性能,發現當拱高與曲梁厚度之比為3.6 時結構具備最優的隔振吸能性能.Chen 等[23]利用彎曲梁結構設計出了多層圓環式的多穩態結構,系統研究了幾何參數對穩定狀態的影響,提出了三層超材料結構實現多穩態功能的有效方法.Yang 等[24]設計制造了可編程的周期性排列一維多穩態圓柱結構,可以實現穩定且可重復使用的構型轉變.

同時,帶隙可主動調控的結構一直都是科研人員關注的熱點,而彎曲梁雙穩態模型的出現為主動調控提供了一條新途徑,在此之前實現主動調控的方式普遍都是通過外加各種物理場的形式來改變特殊胞元材料的密度和模量來實現的.Chen 等[25]提出了基于壓電材料以及電流變彈性體的主動彈性超材料,同時進行了理論分析和數值驗證,可以用來設計目標帶隙結構以及特殊的波導裝置.Xia 等[26]利用聲學傳輸線法(ATLM)研究了溫度對聲學超材料產生帶隙的影響,結果發現溫度變化對結構的色散特性具有顯著影響,為主動控制聲學超材料的設計提供了新的方法.Zhang 等[27]通過在環氧樹脂桿上周期地布置含有負電容的壓電分流單元,構造了壓電聲子晶體桿結構,通過理論和仿真計算證明通過改變不同諧振頻率的壓電分流單元的個數,獲得多個局域共振帶隙,增強帶隙可調諧性.在彎曲梁雙穩態結構提出之后,大量的研究集中在構型轉變對結構色散特性的影響上.Meaud 等[28]研究了彎曲梁雙穩態結構不同構型下的色散關系,仿真結果表明兩種構型下結構的色散特性發生了改變,該結構可以應用于聲學開關.Tan 等[29]提出了一種基于屈曲的可編程負剛度超材料,通過橫向約束實現了結構構型的轉變,結果表明穩態轉換可以調控彈性波的傳播,并指出在主動調控聲學超材料方面引入形狀記憶材料值得嘗試.Liu 等[30]研究了周期性雙穩態結構的非線性彈性響應,特別是沖擊波響應方面,結果表明結構一定程度上可以衰減沖擊波的強度,可以用于精密設備的保護.Hu 等[31]利用形狀記憶材料(SMP)制備了彎曲梁雙穩態結構,結構無需外加物理場的激發就可以實現構型的自主轉變,同時系統地研究了模型的色散關系.針對不同構型的彎曲梁雙穩態結構色散特性研究基本都局限于二維的平面構型之中,而二維的可重構結構在外力驅動調控之下由于其端部缺乏約束以及平面厚度較窄等因素,結構往往會發生橫向變形和面內彎曲,導致達不到穩態轉變的變形要求.Hua 等[32]設計出了圓柱式的空間多穩態結構,探討了多穩態結構作為吸能結構的應用前景并研究了幾何參數對結構吸能性能的影響.Giri 等[33]也對圓柱式多穩態結構進行了研究,主要分析了多層可重構結構中單層幾何參數的設置對整體構型轉變順序的影響,同時也對其吸能性能進行了對比.圓柱式空間可重構結構的提出解決了以往二維平面可重構結構容易產生多余變形的問題,周期性排列的平面可重構結構可以相互為對方提供端部約束.但是針對三維空間構型的可重構結構的研究集中在其力學性能方面,特別是結構的吸能性能,而對其色散特性的研究工作進行得很少.

因此,本文設計了基于彎曲梁結構的六角空間可重構模型,研究其構型轉變過程中的力學特性以及不同構型形式下的色散特性.第一節構建中心受壓直梁模型,從理論出發探明可重構結構構型轉變的基理,并設計了六角的空間可重構結構;第二節介紹了標準拉伸試驗以及結構力學性能及聲學性能方面的仿真計算,并進行了相應的討論分析;第三節總結本文的研究成果.本工作采用數值仿真方法,研究了六角空間雙穩態結構的力學特性與色散特性,以期為后續的進一步研究提供參考數據.

1 理論分析及結構設計

1.1 雙穩態機制研究

基于彎曲梁可重構機制進行理論分析,建立中心受壓、兩端固定的彎曲梁模型,探明穩態轉變的內在機理,彎曲梁模型如圖1 所示.

圖1 雙穩態屈曲梁模型Fig.1 Bistable buckling beam model

梁的基本微分方程為

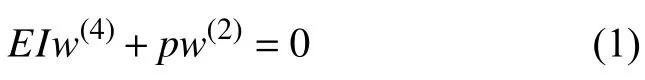
式中,E為材料的楊氏模量,I=bt3/12 為梁的橫截面慣性矩,w為梁的撓度,p為梁的軸向力.其滿足的幾何條件為

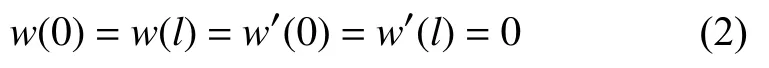
其通解為

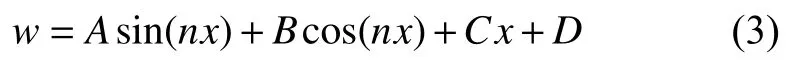
最終求得撓曲線方程的兩類解.第一類為

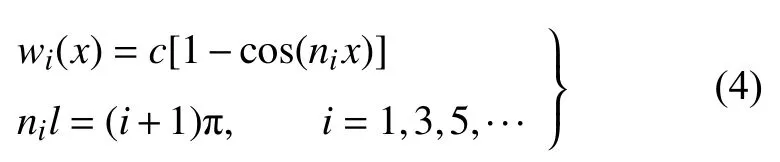
第二類為

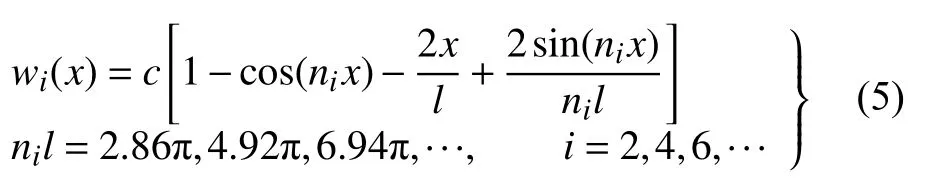
式中c為待定常數.

曲梁的初始形狀為

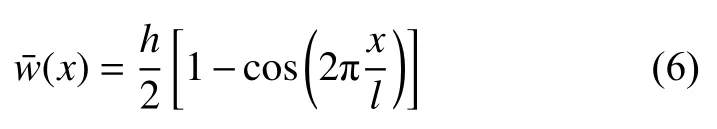
變形過程中軸向變形為dp,則變形過程中曲梁的真實長度為

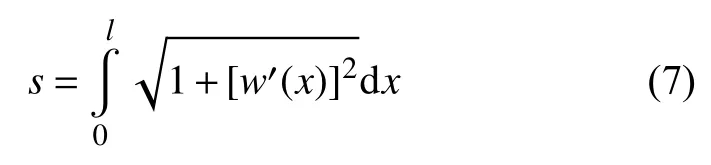
曲梁在受到力f作用變形時,撓曲線可表示為式(4)和式(5)中解的疊加,即

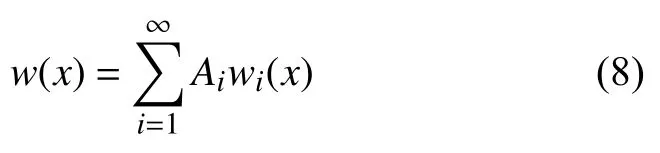
式中,Ai為疊加各項的系數,曲梁中點的位移d可表示為

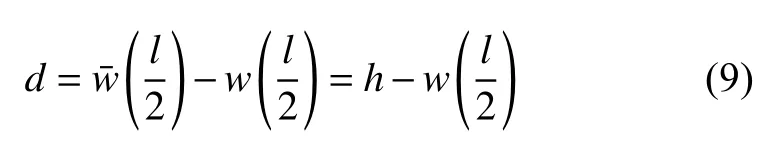
根據胡克定律,軸向力為

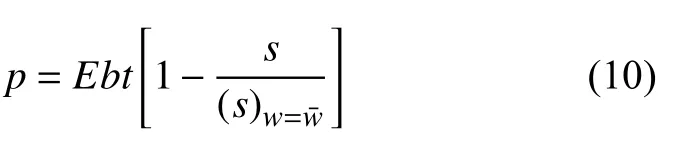
曲梁的軸向變形為dp,在變形過程中由于軸向力壓縮產生的壓縮應變能為

由于彎曲產生的應變能為

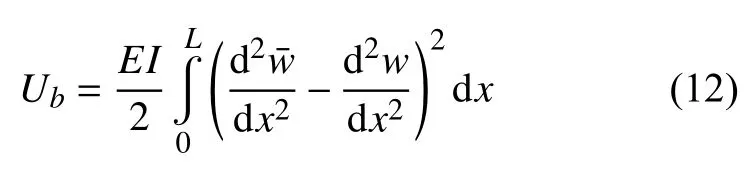
由外力f做功引起的勢能變化為

系統的總能量表達式為

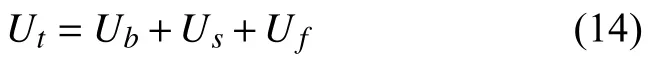
令 ?Ut=0 ,由 ?(Ai)|i=1,5,9,···=0解得各項的系數Ai

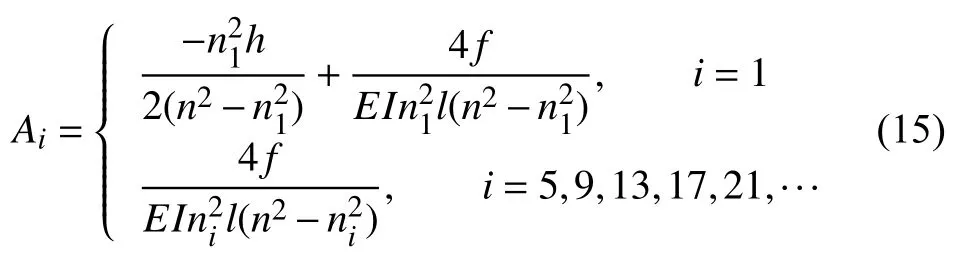
當i=2,3,4,6,7,··· 時,有

在變形過程中軸向力只能連續變化,因此第一種形式的力-位移關系是

由于梁的變形主要取決于前三階屈曲模態,聯立式(9)、式(15)和式(17)并忽略高階模態(即Ai取0),解得

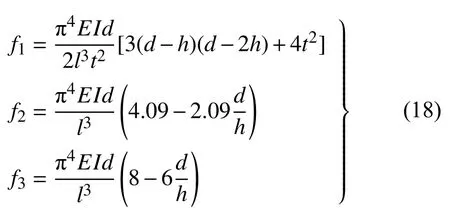
定義拱高厚度比Q=h/t,當Q取值不同時,力-位移曲線也會發生相應變化,如圖2 所示.

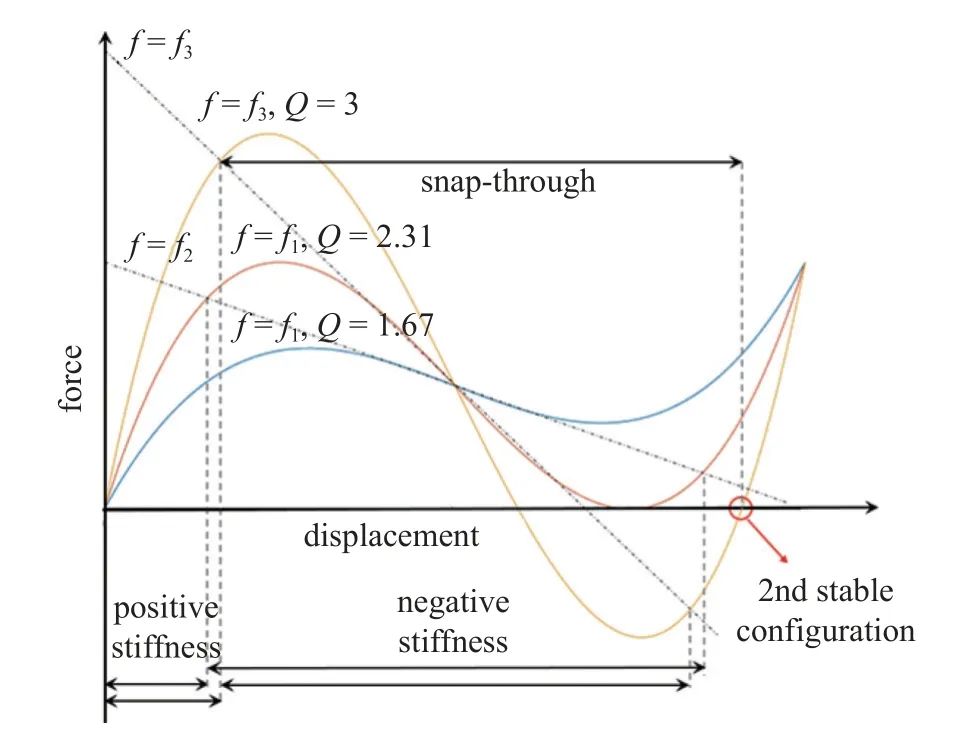
圖2 彎曲梁的不同力-位移特性Fig.2 Different force-displacement behaviors

由力-位移曲線圖可以看出,當Q達到第二階屈曲變形的臨界值2.31 時,力-位移曲線此時正好與x軸相切,Q大于2.31 的情況下,梁的變形情況由第三階屈曲模態決定,比如Q=3 時,變形過程力出現負值,表明結構此時已經具備了雙穩態特性.在發生由第二階屈曲模態和第三階屈曲模態所決定的變形過程中結構具備明顯的正剛度階段以及負剛度階段,特別是在Q=3 的情況下,其負剛度階段即為結構發生突彈跳變(snap-through)的過程,在圖2 中紅圈標注處,當結構力值再次為0 時,此時結構的勢能達到另一個極低點,意味著結構此時轉變為另一個穩定的構型.

1.2 六角型模式轉換結構設計

外力作用下單個二維的可重構結構在變形的過程中往往會發生面內彎曲,而且最大承載力也比較小,這些問題限制了模式轉換功能性材料的應用范圍.因此,為了保證整體結構變形的穩定性,提高結構的承載峰值力,基于二維的可重構結構單胞設計了六角型的模式轉換結構,結構的具體幾何參數如圖3(a)所示,曲梁的跨長為l,拱高為h,自身厚度為t,上下框架結構的寬度均為a,結構整體厚度為b,通過SolidWorks 得到的整體架構如圖3(b)所示.

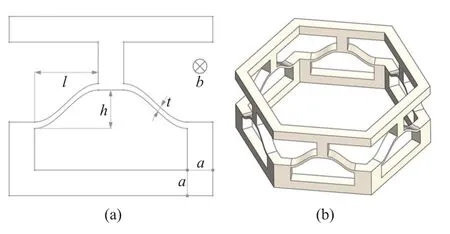
圖3 六角型結構示意圖Fig.3 Hexagonal structure

2 標準拉伸試驗與數值仿真

2.1 標準拉伸試驗

選用萬華化學公司熱塑性聚氨酯彈性體橡膠(TPU)作為制備雙穩態結構的打印材料.TPU 材料的彈性模量可以通過單軸拉伸實驗測得,參考GB/T 528—2009 設計了單軸拉伸試件,試件的幾何尺寸如圖4 所示.

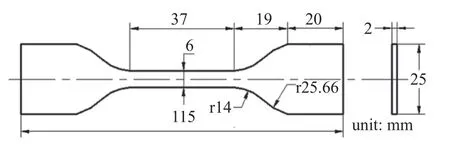
圖4 基于GB/T 528—2009 的拉伸試樣的尺寸Fig.4 Dimensions of tensile specimen based on GB/T 528—2009

為獲得材料的力學參數進行了標準拉伸試驗,拉伸的速度設為20 mm/min,采用引伸計記錄單軸拉伸過程中標定段的位移,最終測得試樣的平均彈性模量為145.2 MPa,泊松比為0.46.圖5 為測試照片.

圖5 標準拉伸測試Fig.5 Standard tensile test

2.2 結構力學性能數值仿真分析

通過雙穩態機制的理論分析得知: 彎曲梁單胞的幾何參數(彎曲梁的厚度t、拱高h)對結構的力學性能起著決定性作用,為探明六角型結構幾何參數對其整體力學性能的影響,采用控制變量方法,設定t=1 mm,b=4 mm,l=10 mm,h從2 mm 到9 mm,步長為1;a為1 mm 到5 mm,步長為0.5.利用ABAQUS/Explicit 研究不同幾何參數下結構變形過程中的力學行為.仿真過程中通過在模型上表面耦合點施加位移載荷的方式實現整體結構的變形,同時在模型底部施加固定約束(如圖6 所示).依照標準拉伸測試測得數據,采用 neo-Hookean 超彈性模型對材料本構進行擬合,網格劃分選用8 節點線性減縮積分實體單元(C3D8R).

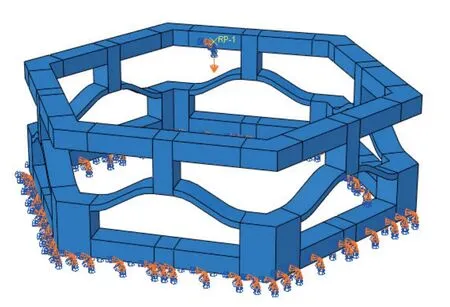
圖6 ABAQUS 仿真示意圖Fig.6 ABAQUS simulation schematic diagram

對不同幾何參數六角型結構進行系統化的仿真分析,得到了兩者之間對應關系的相圖(圖7).

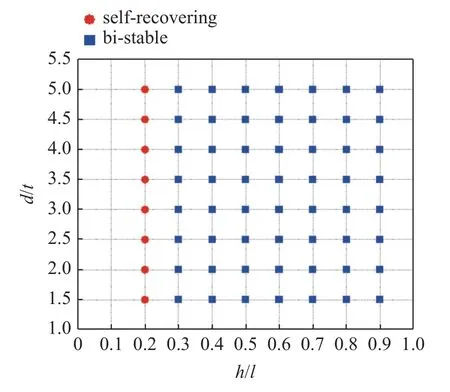
圖7 幾何參數與力學性能相圖Fig.7 Phase diagram of geometric parameters and mechanical properties

結果顯示當曲梁自身寬度t固定為1 mm,跨長l固定為10 mm,其拱高h與曲梁跨度l比值比較小如0.2 時,隨著下壓位移的增加結構呈現出負剛度特性,但作用力始終為正值,說明結構此時具備自恢復特性;而當兩者比值達到0.3 后,隨著下壓位移的增加結構也呈現出負剛度特性,不同的是作用力出現了負值的情況,說明結構具備雙穩態特性.通過幾何參數與力學性能之間關系的研究分析,可以根據目標性能設計出構型合理的可重構超材料結構.

2.3 結構色散關系數值仿真分析

通過上述力學性能數值仿真分析得知具備雙穩態特性的結構可以實現可控變形的能力,圖8 展示了六角型空間結構的構型轉變行為,而其構型的改變會導致色散特性出現變化,為了研究構型改變對色散特性的具體影響情況,利用有限元數值仿真對雙穩態結構進行了色散關系分析,在上下表面施加floquet 周期性邊界條件,對結構豎直方向(z方向)色散特性進行數值計算,得到不同構型下結構的色散曲線.圖9 和圖10 分別給出了a=2 mm,h=4 mm 情況下拉伸和壓縮兩種構型下的色散關系曲線.

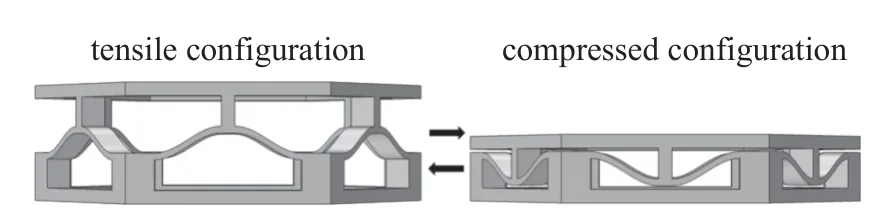
圖8 幾何構型轉變Fig.8 The geometric configuration switching

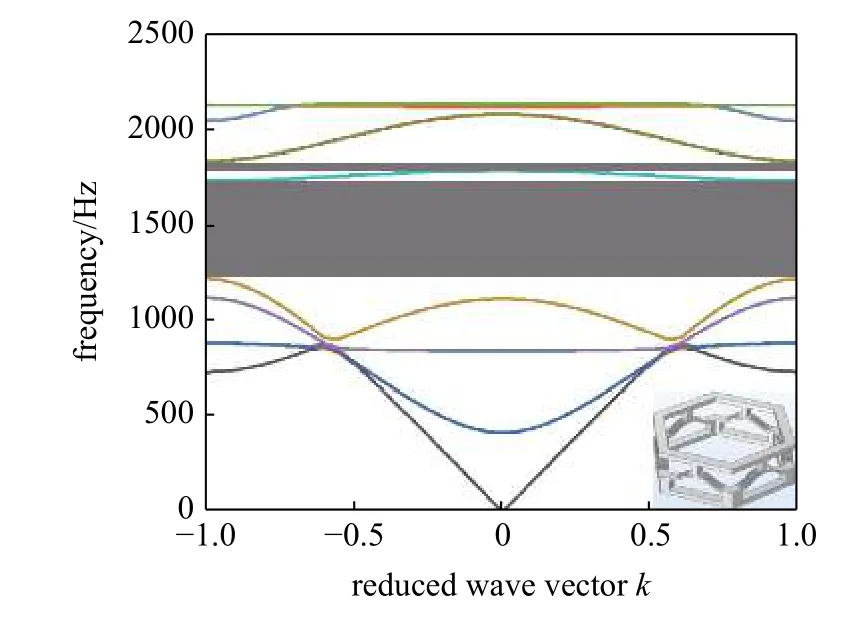
圖9 拉伸構型下的色散關系曲線Fig.9 Dispersion relationship curve in stretched configuration

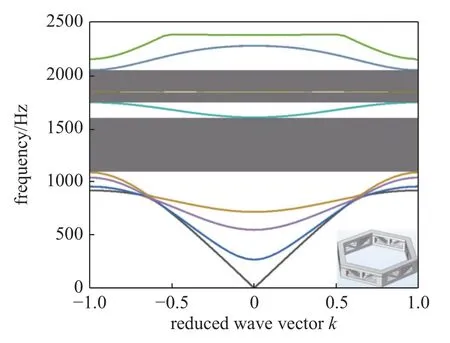
圖10 壓縮構型下的色散關系曲線Fig.10 Dispersion relationship curve in compressed configuration

結果顯示在拉伸構型下結構在計算頻率范圍內形成了兩個完全帶隙,分別位于1224.29～1740.16 Hz,1794.16～1842.44 Hz.其中第一帶隙位于第六支與第七支色散曲線之間,第二帶隙位于第七支與第八支色散曲線之間.而壓縮構型下在計算頻率范圍內則產生了三個帶隙,分別位于1087.22～1603.46 Hz,1745.19～1846.91 Hz 和1850.53～2047.68 Hz.其中第一帶隙介于第六支與第七支色散曲線之間,第二帶隙介于第七支與第八支色散曲線之間,第三帶隙介于第九支與第十支色散曲線之間.可以看出結構構型從拉伸轉變為壓縮的過程中,結構的第一帶隙向低頻方向移動,壓縮構型下的第二帶隙相比于拉伸情況下禁帶頻率范圍有所增加,另外由于構型的轉變導致結構的晶格常數發生了變化,從而改變了其色散模式,在壓縮構型的情況下產生了新的第三帶隙.

仿真結果初步說明可以通過結構構型的調整來改變結構的波動特性,實現對波的主動控制.此外拉伸構型下兩個帶隙中心頻率對應的波長分別為0.282 m,0.198 m.而拉伸構型下晶格尺寸為0.018 m,說明結構可以在亞波長尺度下形成帶隙,可以推斷出這些帶隙是由局域共振機制引起的.為了進一步驗證六角型雙穩態結構的帶隙形成機制,對其截至頻率處的振動模態進行了研究分析,如圖11 所示,從左至右依次給出了拉伸構型下兩個帶隙截至頻率處的振動模態圖,可以看出在第一帶隙的振動模態主要表現為上下質量塊的振動,而在第二帶隙的振動模態圖中可以看到框架結構保持靜止而單胞的中間連接部分在振動,結合之前對中心頻率處波長的計算數據可以判定拉伸構型下的第一帶隙是由于上下框架結構作為質量塊振動引起的局域共振,而第二帶隙則是由于彎曲梁部分振動引起的局域共振.同時構建了兩種構型的動力學特性分析模型以進行頻率響應(frequency response)計算,如圖12 所示兩者的動力學特性分析模型均為單胞沿z軸周期性排布形成的,陣列數量為10.將模型中底部單胞下表面的邊界定義為激勵位置,施加沿z軸正向的指定加速度,加速度數值為0.1 mm/s2,并在此邊界定義積分條件作為頻響計算的初始值.同樣將模型端部第一個單胞的下表面作為響應位置,定義積分條件作為頻響計算的響應值.

圖11 模態振型Fig.11 Modal diagram

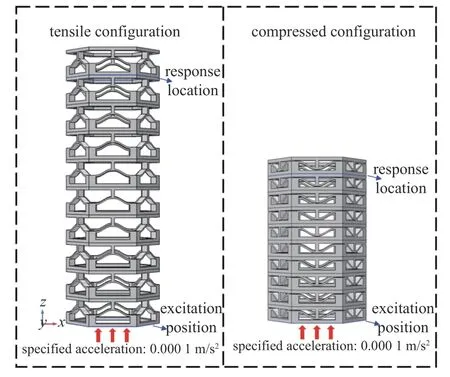
圖12 色散特性分析模型Fig.12 Dispersion characteristic analysis model

得到的結果如圖13 所示,頻響計算更為直觀地展現了結構構型改變對自身色散特性帶來的變化,從拉伸構型到壓縮構型的轉變過程中,帶隙是朝著低頻方向移動的.

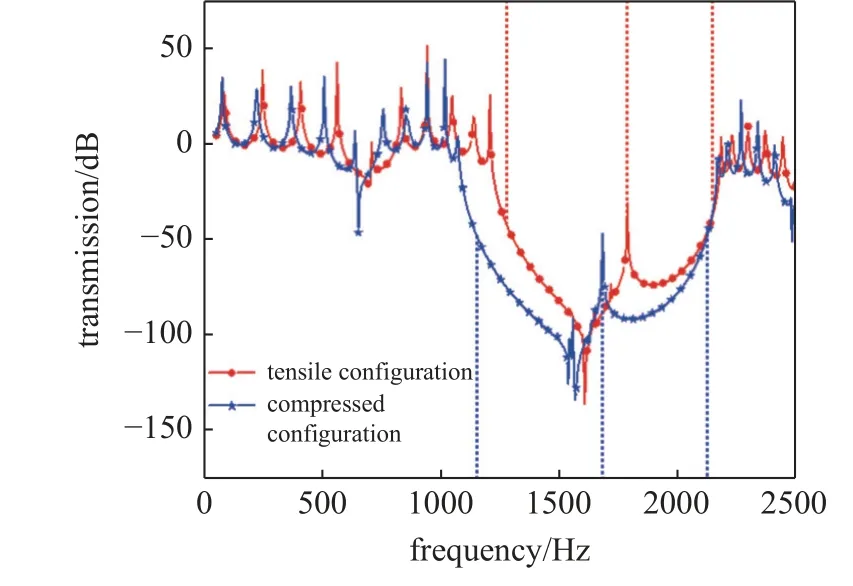
圖13 頻響曲線Fig.13 Frequency response curve

另外,對其他不同幾何參數的結構也進行了相應的帶隙計算分析,通過柱狀圖的形式展示了帶隙隨著幾何參數的變化情況,如圖14～圖17 所示.

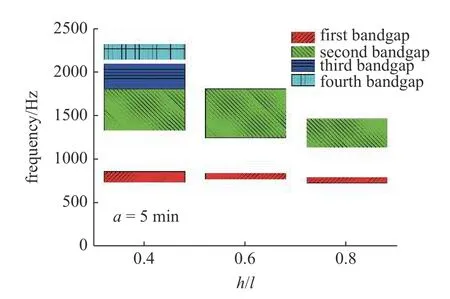
圖14 拉伸構型下帶隙變化柱狀圖Fig.14 Histogram of band gap change in tensile configuration

圖14 為t=1 mm,a=5 mm,l=10 mm 情況下,結構在拉伸構型下產生的帶隙隨著拱高h的變化示意圖,在h=4 mm 即h/l=0.4 時結構產生了四個帶隙,分別位于744.86～867.38 Hz,1336.86～1815.21 Hz,1820.92～2106.35 Hz 以及2148.52～2325.64 Hz 處;當h為6 mm 即h/l=0.6 時,結構僅產生了兩個帶隙,分別位于777.95～852.12 Hz,1255.36～1814.53 Hz處;當h為8 mm 即h/l為0.8 時,結構產生了兩個帶隙,位于735.93～803.74 Hz,1145.05～1468.66 Hz 處.可以看出在拉伸構型下,隨著拱高h的增加,結構的帶隙總體是朝著低頻移動的,而且h為4 mm 時結構在1800 Hz 之上產生的兩個帶隙隨著h的增加消失了.圖15 為t=1 mm,a=5 mm,l=10 mm 情況下,結構在壓縮構型下產生的帶隙隨著拱高h的變化示意圖,可以看出隨著拱高h的增加,帶隙數量逐漸減少,當h為8 mm 時結構僅產生了一個帶隙.

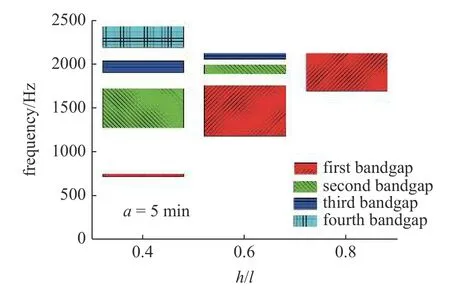
圖15 壓縮構型下帶隙變化柱狀圖Fig.15 Histogram of band gap change in compressed configuration

圖16 給出了t=1 mm,h=6 mm,l=10 mm 的情況下,結構在拉伸構型下產生的帶隙隨著框架寬度a的變化示意圖.當a為2 mm 即a/t=2 時結構產生了一個帶隙,位于1254.93～1665.67 Hz 處;當a為3 mm 即a/t=3 時結構也產生了一個帶隙,位于1216.04～1772.81 Hz 處;當a為4 mm 即a/t=4 時結構產生的帶隙位于1270.88～1836.05 Hz 處;當a為5 mm 即a/t=5 時結構產生了兩個帶隙,其中第一帶隙位于777.95～852.12 Hz,第二帶隙位于1255.36～1814.53 Hz 處.總體來看框架寬度對結構的帶隙的影響作用甚微,除了在a=5 mm 的情況下產生了一個新帶隙之外,其他情況下帶隙的位置和帶寬變換均不大.圖17 給出了t=1 mm,h=6 mm,l=10 mm 的情況下,結構在壓縮構型下產生的帶隙隨著框架寬度a的變化示意圖.可以看出與拉伸構型相同,框架寬度a對結構帶隙的影響不大,隨著a的持續增加,帶隙總體是朝著高頻移動的,但移動幅度也很有限.

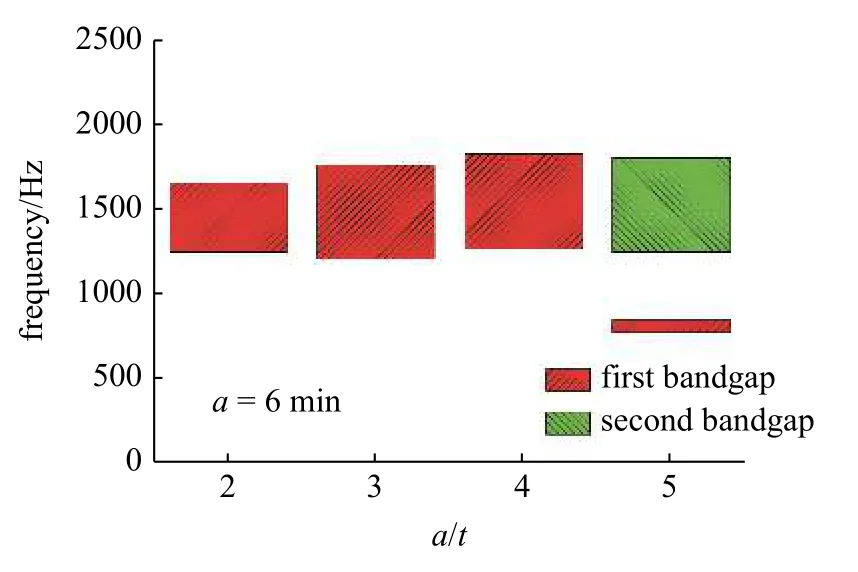
圖16 拉伸構型下帶隙變化柱狀圖Fig.16 Histogram of band gap change in tensile configuration

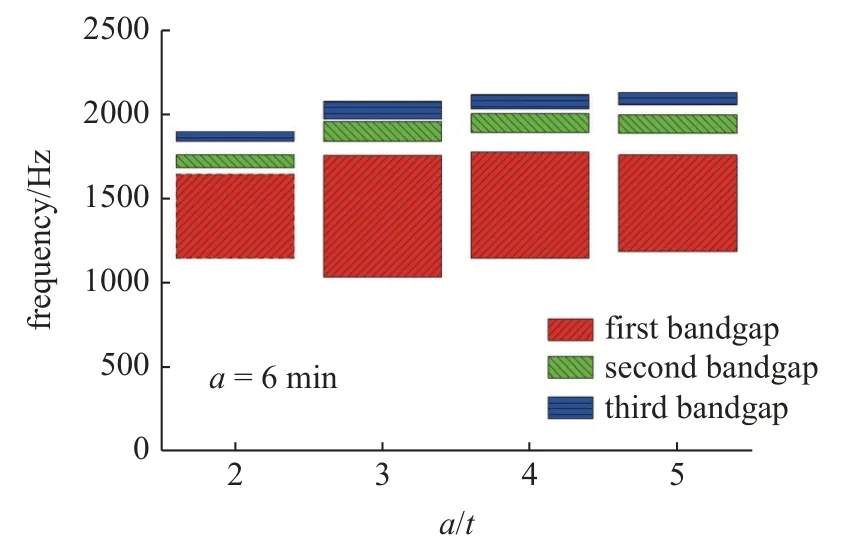
圖17 壓縮構型下帶隙變化柱狀圖Fig.17 Histogram of band gap change in compressed configuration

結構構型轉換及幾何參數的變化對色散關系產生的影響證明,可以通過改變具備雙穩態特性結構的構型來主動調控波的傳輸特性,另一方面也可以根據目的帶隙來逆向設計合理幾何參數的雙穩態結構.

3 結論

本文基于彎曲梁雙穩態結構設計了六角型可重構結構,并利用有限元數值仿真進行了力學性能與色散特性分析.首先研究了六角型可重構結構幾何參數對其整體力學性能的影響,得到了具備自恢復、雙穩態特性的具體結構幾何參數;之后在具備雙穩態特性結構的基礎上進行了兩種構型下的色散關系分析,研究構型變化對結構色散關系的影響并進行了相應的頻率響應計算.得到的結論可以總結如下.

(1) 通過研究幾何參數對結構力學性能的影響,得到了具備不同力學性能的結構幾何參數,在彎曲梁自身寬度t為1 mm 且跨度l為10 mm 的基礎上,當h/l大于等于0.3 時即h取值大于等于3 mm 時結構即呈現雙穩態特性,而h取值為2 mm 時結構則呈現自恢復特性.

(2) 具備雙穩態特性的結構在兩種構型下的色散曲線發生明顯變化,在t=1 mm,a=2 mm,h=4 mm,l=10 mm 的情況下,其壓縮構型下的帶隙相比于拉伸構型下,具備明顯的朝向低頻移動趨勢.兩種構型幾何特征的改變導致其晶格常數出現差異,進而影響到結構整體的色散特性,導致帶隙的位置、范圍以及數量均發生變化.

(3) 通過對六角型可重構結構力學性能和色散特性的分析,初步證明可以通過調整結構的幾何參數實現對整體力學性能的主動設計和色散特性的主動調控,可以根據應用需求設計合適的結構構型.