基于CFS-PML 的高階有限元在地質雷達數值模擬中的應用研究

韓曉冰 郭濤 李航 梁冰洋 周遠國

（西安科技大學通信與信息工程學院,西安 710600）

引言

地質雷達(ground penetrating radar，GPR)數值模擬是用電磁計算來研究地下介質分布規律的一種方法，通過將數值計算獲得的模擬結果與實際研究區域的檢測結果進行對比，能夠有效地分析GPR 技術的實際應用效果，可為實際應用中檢測數據的地質解釋奠定理論基礎，該方法逐漸成為近年來地球物理勘探領域的研究熱點[1-3].常用的數值模擬方法包括有限差分法[4]、有限元法(finite element method,FEM)[5-6]等.在GPR 建模過程中，為了減少計算量，通常會采用完美匹配層(perfectly matched layer，PML)[7-8]對模型進行截斷，PML 的吸收效果直接影響整個模型的計算精度.

然而，PML 邊界條件在數值模擬過程中，仍存在一些復雜問題，例如，對倏逝波都不能很好地吸收[9]，因此在文獻[10]中提出了基于單軸完美匹配層(uniaxial perfectly matched layer，UPML).UPML 不需要對吸收介質中的波場進行分裂，因此，計算簡潔、內存消耗降低.并且在衰減系數中引入了吸收因子，使得UPML 邊界能夠較好地衰減倏失波、低頻波等干擾波.文獻[11]利用高階時域有限差分(finitedifference time-domain,FDTD)法結合UPML 邊界條件實現GPR 正演數值模擬，優化迭代UMPL 吸收邊界，完善了三維模擬在計算效率與吸收效果的雙重要求.文獻[12]采用了基于交替方向隱式FDTD(alternating direction implicit-FDTD,ADI-FDTD)法，引入UMPL 消除了截斷邊界處的強反射現象.但UMPL 媒質的角形區域仍需頻時轉換，迭代求解大型線性方程組，增加了內存消耗.

雖然UPML 對于倏失波、低頻波等干擾波具有一定的吸收效果，但吸收效果依然不是特別完美.復頻移PML(complex frequency shifted-PML，CFS-PML)技術主要利用坐標展寬來增強倏失波在場中的衰減，其可以吸收低頻信號在邊界表面的反射，同時對大角度掠射波有很好的吸收效果[13](主要通過頻移參數 α降低掠射波，入射到PML 界面時產生的非均勻波).文獻[14]利用雙線性變換技術增加CFS 因子，以避免場分裂情況，并且實現了柱坐標系下的CFS-PML吸收邊界，與傳統UMPL 邊界相比，CFS-PML 邊界條件具有更好的吸收性能.文獻[15]實現了CFSPML 在三維海洋可控源電磁建模中的應用，有效地抑制住了人工邊界效應，與Dirichlet 邊界相比，降低了內存消耗，提高了計算效率.文獻[16]改進了CFSPML 邊界條件，并成功將其應用于瞬變電磁法的三維有限差分虛擬波域(finite difference-fictitious wave domain,FD-FWD)建模中.采用均勻半空間模型，數值結果表明在FD-FWD 中，CFS-PML 邊界條件具有比PML 更好的吸收效果.

GPR 數值模擬時，吸收邊界產生的人為反射波會影響整個模型的計算精度.為進一步改善GPR 三維數值模擬邊界條件的吸收效果，同時優化計算效率，本文引入高階有限元法(higher order finite element method，HO-FEM).HO-FEM 是FEM 的一種改進形式，不同之處在于其采用高階正交多項式作為基函數[17].一方面提高了算法的效率，另一方面提高了離散網格內的建模精度，降低建模時對網格的依賴，且兼顧了常規FEM 對復雜地質模型模擬的靈活性[18]，該方法可使計算精度較高且計算量大幅減少[19].相較于HO-FEM 利用PML 作為吸收邊界[20]，CFSPML 能更有效地處理倏失波衰減的問題.HO-FEM算法雖然已經應用于多種電磁場數值模擬中[21-22]，但在GPR 三維數值模擬中的研究尚未涉及.因此，本文做了以下兩部分工作：1)將復頻移坐標拉伸系統引入到PML 域內，使得頻移參數 α對倏失波進行有效衰減；2)將CFS-PML 算法與HO-FEM 法進行結合，以此來求解三維GPR 數值模擬問題，提高計算精度與效率.

1 理論方法

1.1 HO-FEM 方法

從微分形式麥克斯韋方程組出發，利用時變因子 eiwt，得到如下控制方程：

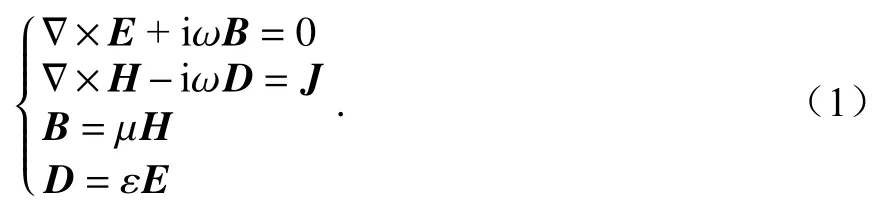
式中：E為 電場強度，V/m；ω為角頻率；B為磁通量密度，Wb/m2；H為磁場強度，A/m ；D為電通量密度，C/m2；J為電流密度，A/m2；μ 為磁導率；ε為介電常數.對式(1)中第二個方程取旋度，得到關于磁場矢量赫姆霍茲方程

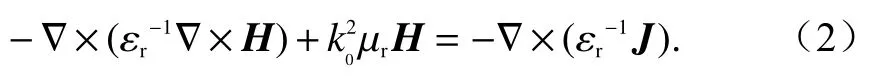
式中：εr為相對介電常數；為真空中的波數；μr為相對介磁常數.與FEM 相同，對整個計算域進行區域離散，得到很多子區域，稱之為單元.采用伽遼金加權殘差法處理式(2)，令e單元內的加權殘差積分為零，即

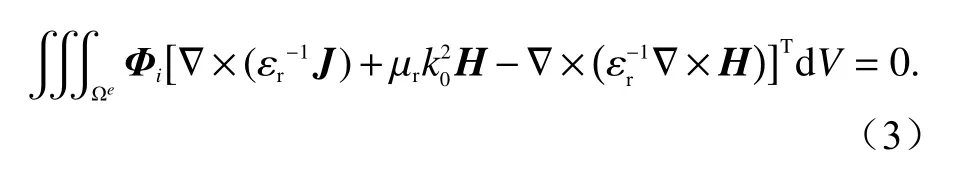
式中：Φi為加權基函數；Ωe是單元計算域.對式(3)展開如下：

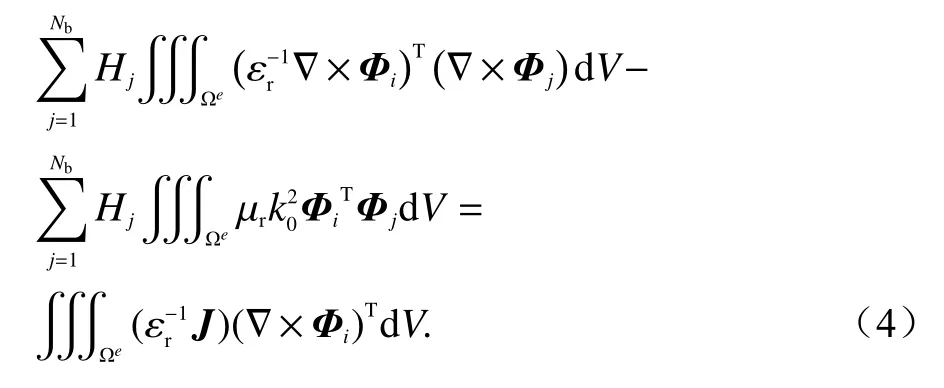
式中：Nb表示單元外邊界棱邊數.使用伽遼金加權殘差法時，規定采用的加權基函數和近似解展開函數相同，這里采用高斯-洛巴托-勒讓德(Gauss-Lobatto-Legendre,GLL)高階插值多項式作為加權基函數，一維參考空間上的N(N≥2)階GLL 基函數

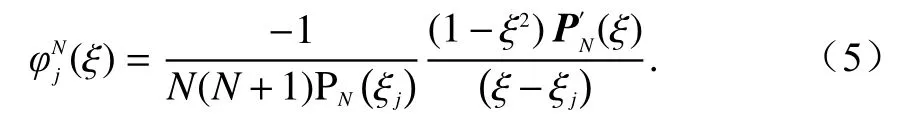
式中：PN(ξj)為Legendre 多項式；ξj為GLL 插值節點；j=0,1,···,N.

將所有單元進行集成，離散系統矩陣如下：

由式(1)控制方程推導得到磁場矢量赫姆霍茲方程，結合式(3)伽遼金加權殘差法，引入式(5)中的GLL 高階插值多項式，得到式(6) HO-FEM 的離散系統矩陣形式，最終我們將HO-FEM 算法應用于整個計算域內.

1.2 HO-FEM-CFS-PML 計算方法

CFS-PML[23]的主要思想是在人工邊界內水平和垂直方向引入一個復雜的坐標拉伸系統.例如，x方向拉伸因子e(x)為

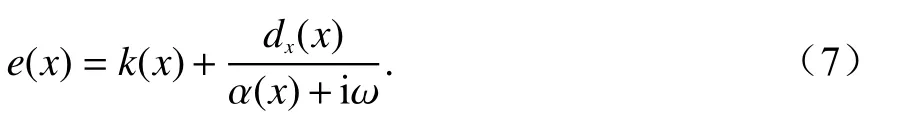
在電磁建模中主 要考慮到 參數k(x)和dx(x)，且k(x)和dx(x)均取正數，在本文中k(x)取值為25，與 文獻[16]一致.

α(x)參數的本質是吸收倏逝波并改善掠射角處的吸收性能[24]，表達式為

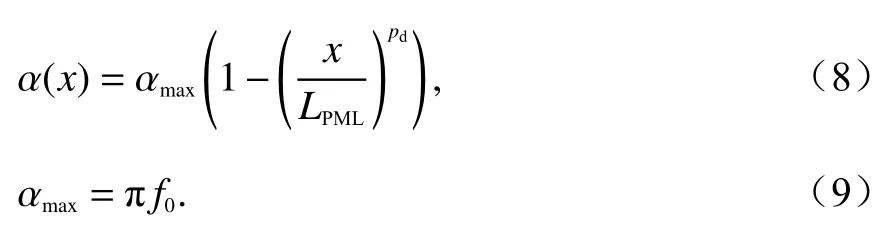
式中：LPML為 每側PML 區域厚度；pd取值一般為2 或3[16]；f0為電磁波主頻率.

dx(x)作為x方向的衰減阻尼因子，表達式為

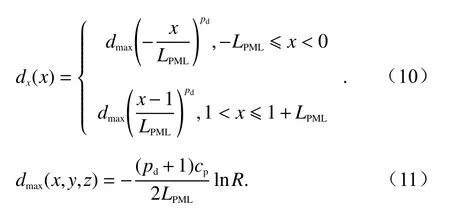
式中：cp為 電磁波傳播速度；R是反射系數.式(10)中的1 為計算域x方向長度縮放為1.從式(10)看出，上述公式中dx(x)須在PML 域內取值.對于三維模型而言，PML 域內擁有三種媒質分區，分別是平面區、棱邊區和角頂區，每個分區都應有d(x)作為衰減阻尼因子進行電磁波的衰減.

在HO-FEM 中引入CFS-PML 后，赫姆霍茲方程可以表示為

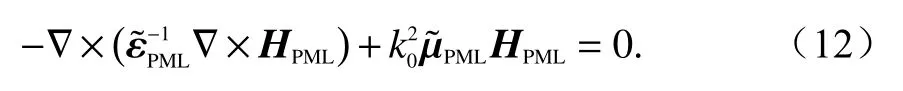
式(12)只針對PML 域內赫姆霍茲方程式.為使PML內邊界與計算域外邊界形成阻抗匹配，引入CFSPML 方法后三維空間中的相對介電張量以及相對介磁張量為：

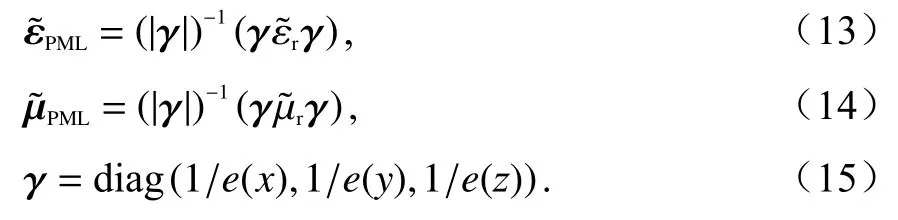
結合HO-FEM 方法，采用伽遼金加權殘差法處理，將式(6)中的質量矩陣和剛度矩陣修正為：

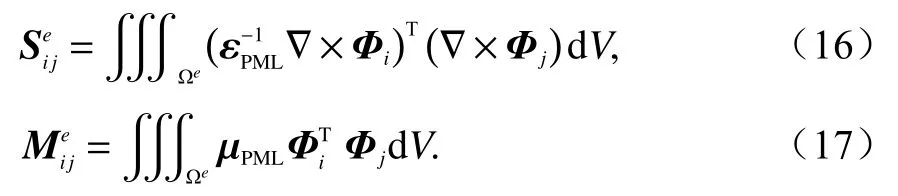
通過以上公式，我們將CFS-PML 復頻移坐標拉伸系統引入到HO-FEM 中的PML 域內，對坐標空間中的電性參數進行復頻移拉伸，從而改善介質本構張量的矩陣特性，增強了整個PML 域對倏逝波的吸收性能.本文并未描述參考空間與物理空間的轉換，具體可參考文獻[20].

2 數值算例

在這一節中，我們設計了兩個GPR 模型，第一個模型采用三維分層介質結構，第二個模型采用三維復雜異常體介質結構.將本文的CFS-PML 方法與傳統PML 方法在數值精度上做對比，為方便起見，兩種算例都采用線源作為發射源，極化方向都為y方向，并與商業軟件WCT 進行比較，來驗證該方法的準確性.同時，對比特定頻率下反射誤差、相對誤差，來驗證本文算法的有效性和精確性.所有算例的仿真都在Intel(R) Xeon(R) Gold 6248R 的CPU 工作平臺進行.

2.1 分層介質GPR 模型

算例1 三維分層介質GPR 模型如圖1 所示，計算區域為4 m×4 m×2 m.以o為坐標原點，z=1 m 為分界面，規定三個方向均為正方向.上層空間為空氣，空氣層厚度1 m.下層空間為土壤，并且在分界面下方0.5 m 處設置水平層厚0.1 m 的礦體.在分界面上方0.125 m 處，沿x方向兩端設置50 個接收點，每點相距0.08 m，接收點中心位置坐標為(2，2，1.125).發射頻率設置為40 MHz，電流強度為25 A，長度為1 m的發射線源沿y軸放置于分界面上方0.01 m 處，其中心位置坐標為(2，2，1.01).表1 給出了算例1 具體的電性參數[25].

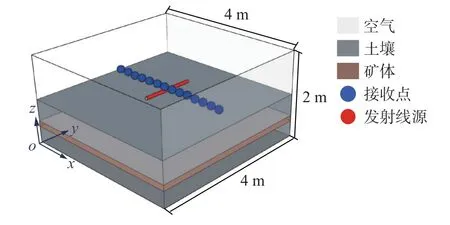
圖1 分層介質GPR 模型Fig.1 Layered media GPR model

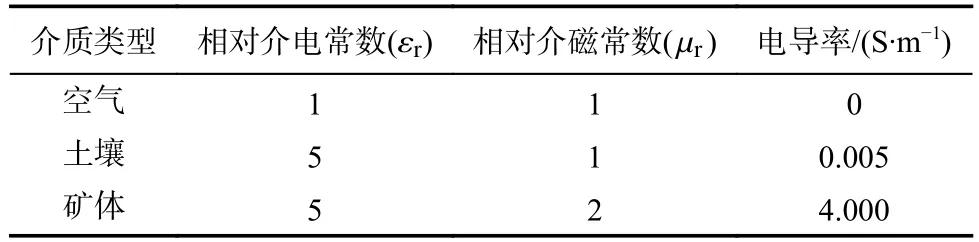
表1 算例1 電性參數Tab.1 Electrical parameters of case 1

由圖2 可知，兩種邊界條件的數值模擬結果均表明HO-FEM 算法應用在GPR 數值模擬時具有較高精度.其中LMGF 求解器為WCT 中分層介質格林函數，主要應用于分層介質的電磁仿真.

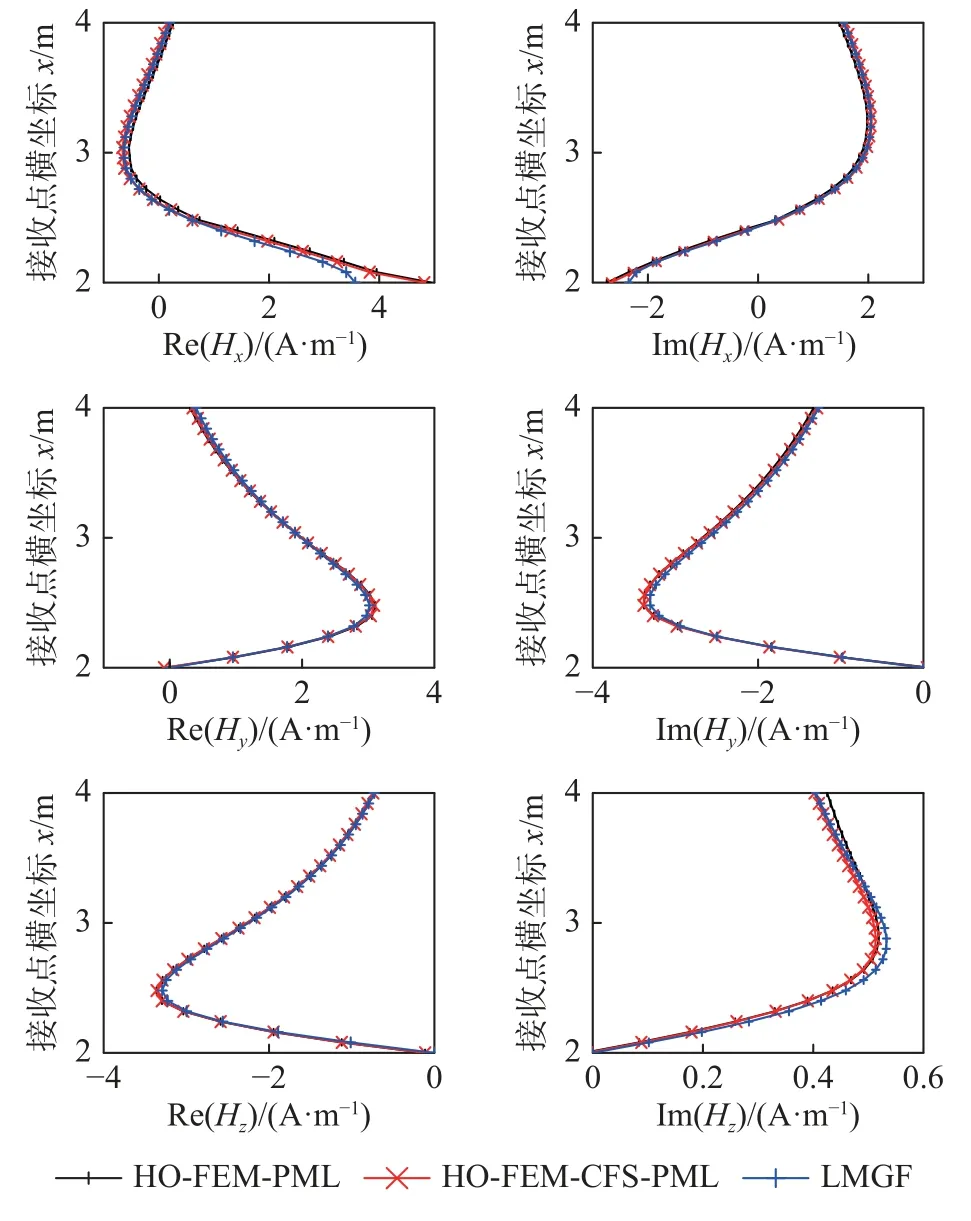
圖2 算例1 各接收點處磁場強度實部和虛部模擬結果Fig.2 Simulation results of the real and imaginary parts of the magnetic field strength at each reception point(case 1)

本文算法反射誤差理論計算公式采用文獻[26]方法，如式(18)所示：

式中：Hi為 觀測點對應的磁場強度；為解析解中每個觀測點對應的磁場強度；為解析解中磁場強度的最大值.

觀察圖3 的反射誤差可知，由于頻移參數 α的影響，CFS-PML 相比于傳統PML 計算的各分量能夠降低10～30 dB.由圖4 可以看到，Hx、Hy、Hz相對誤差分別小于0.72%、0.63%、0.46%，表明CFS-PML 吸收邊界有效地抑制了人工邊界效應，使得吸收性能更加優異.因此，本文所使用的CFS-PML 吸收邊界在整體的接收點處所得的效果要優于PML 吸收邊界.

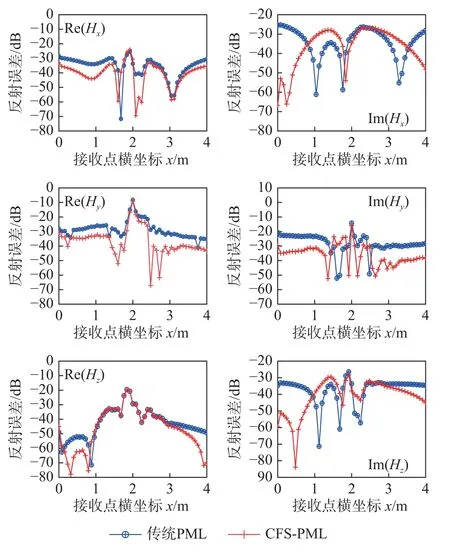
圖3 算例1 各接收點處磁場強度實部和虛部反射誤差對比Fig.3 Comparison of real and imaginary reflection errors of magnetic field intensity at each reception point(case 1)

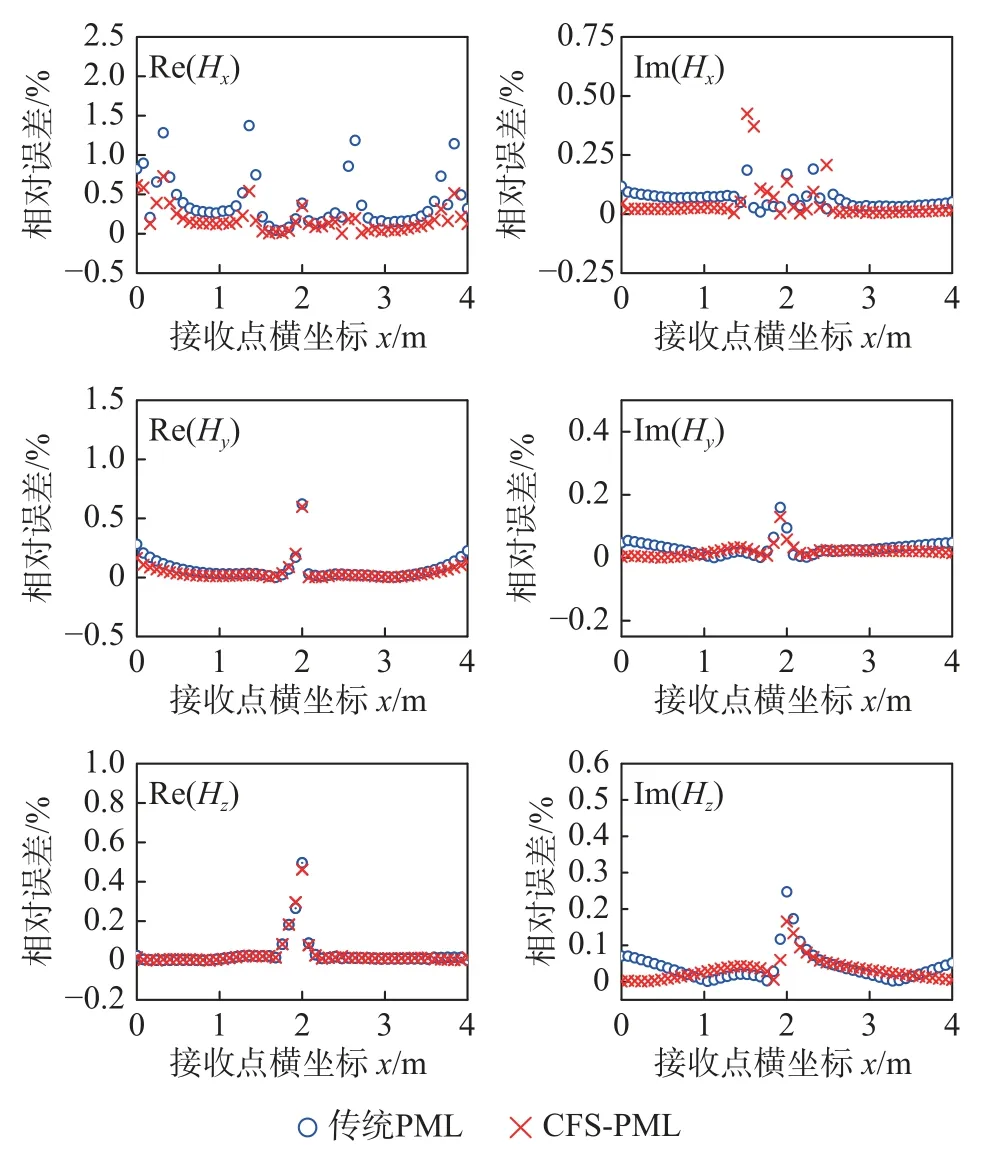
圖4 算例1 各接收點處磁場強度實部和虛部相對誤差對比Fig.4 Comparison of the relative errors of the real and imaginary parts of the magnetic field strength at each reception point(case 1)

與此同時，在本次算例中，CFS-PML 方法與傳統PML 方法的計算耗時分別為18 044 s 和21 734 s，時間節省約為17%；內存消耗分別約為9.8 GB 和11.0 GB，內存節省約為11%.

2.2 起伏地巖GPR 模型

算例2 三維起伏地巖GPR 模型如圖5 所示，計算區域為4 m×4 m×4 m.以o為坐標原點，z=2.5 m為分界面，規定三個方向均為正方向.上層空間為空氣，空氣層厚度1.5 m，下層空間土壤厚度為1.1 m，地巖隆起部分上方寬度為0.5 m，隆起高度為0.12 m，地巖未隆起的厚度為1.4 m.在模型結構上采用的是不規則網格剖分，假設在巖層下方存在一個棱柱形異常體，用以模擬地質空洞.發射中心頻率設置為62 MHz，電流強度為25 A，長度為1 m 的發射線源沿y軸放置在分界面上方0.01 m，發射線源中心位置坐標為(2，2，2.51).接收點中心位置坐標為(2，2，2.625)，采用50 個接收點，間隔為0.08 m，沿著x方向展開長度為4 m.表2 給出了算例2 具體的電性參數[25].采用商業軟件WCT 中CN-FDTD 算法與本文提出的算法進行對比.

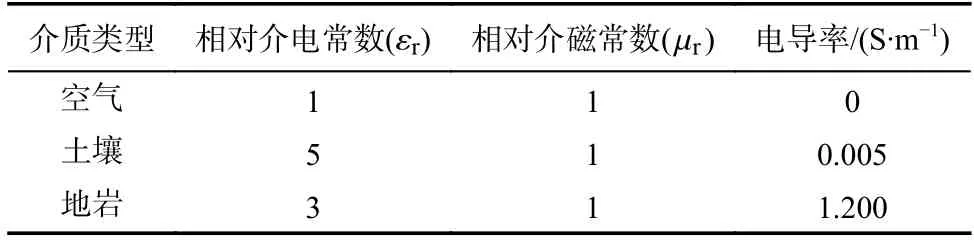
表2 算例2 電性參數Tab.2 Electrical parameters of case 2

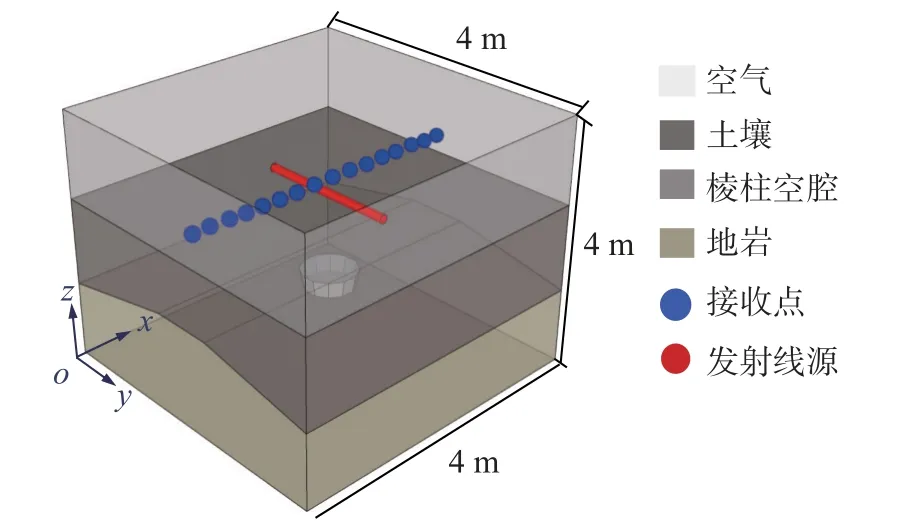
圖5 起伏地巖GPR 模型Fig.5 GPR model of uphill terrane

算例2 雖然受地形改變的影響，但通過對比CNFDTD 算法結果，HO-FEM 算法仍能保持高精度.在測試過程中可以看到，PML 吸收效果并不能達到100%的吸收效率，但從實驗結果來看，圖6 觀察到磁場強度變化較快的區域，CFS-PML 仍能很好地吻合CN-FDTD 結果，表現出較高的精度.圖7 展示了傳統PML 與CFS-PML 在觀測點的反射誤差，從中可以看到CFS-PML 的反射誤差相比PML 較小.三維起伏地巖模型含有復雜有耗的結構，并且采用的不規則網格剖分也會使得傳統的PML 邊界產生一定的誤差，然而CFS-PML 中的頻移參數 α使截斷區域產生頻率相關的衰減，提高掠射角處吸收性能，使得CFS-PML 在傳統的PML 基礎上反射誤差能夠降低10 dB 左右，并且相對誤差能夠控制在合理的范圍.從圖8 可以看出CFS-PML 邊界條件下Hx、Hy、Hz相對誤差分別小于0.99 %、0.52 %、0.74 %，也體現了較高的精度.與此同時，算例2 中，CFS-PML 方法與傳統PML 方法的計算耗時分別為54 243 s 和77 211 s，時間節省約為30%；內存消耗分別約為14.6 GB 和16.8 GB，內存節省約為14%.

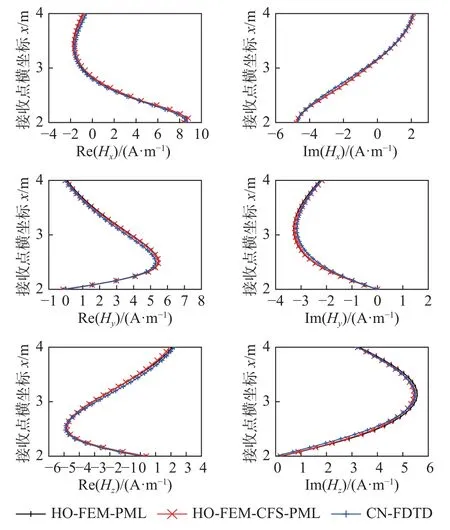
圖6 算例2 各接收點處磁場強度實部和虛部模擬結果Fig.6 Simulation results of the real and imaginary parts of the magnetic field strength at each reception point(case 2)

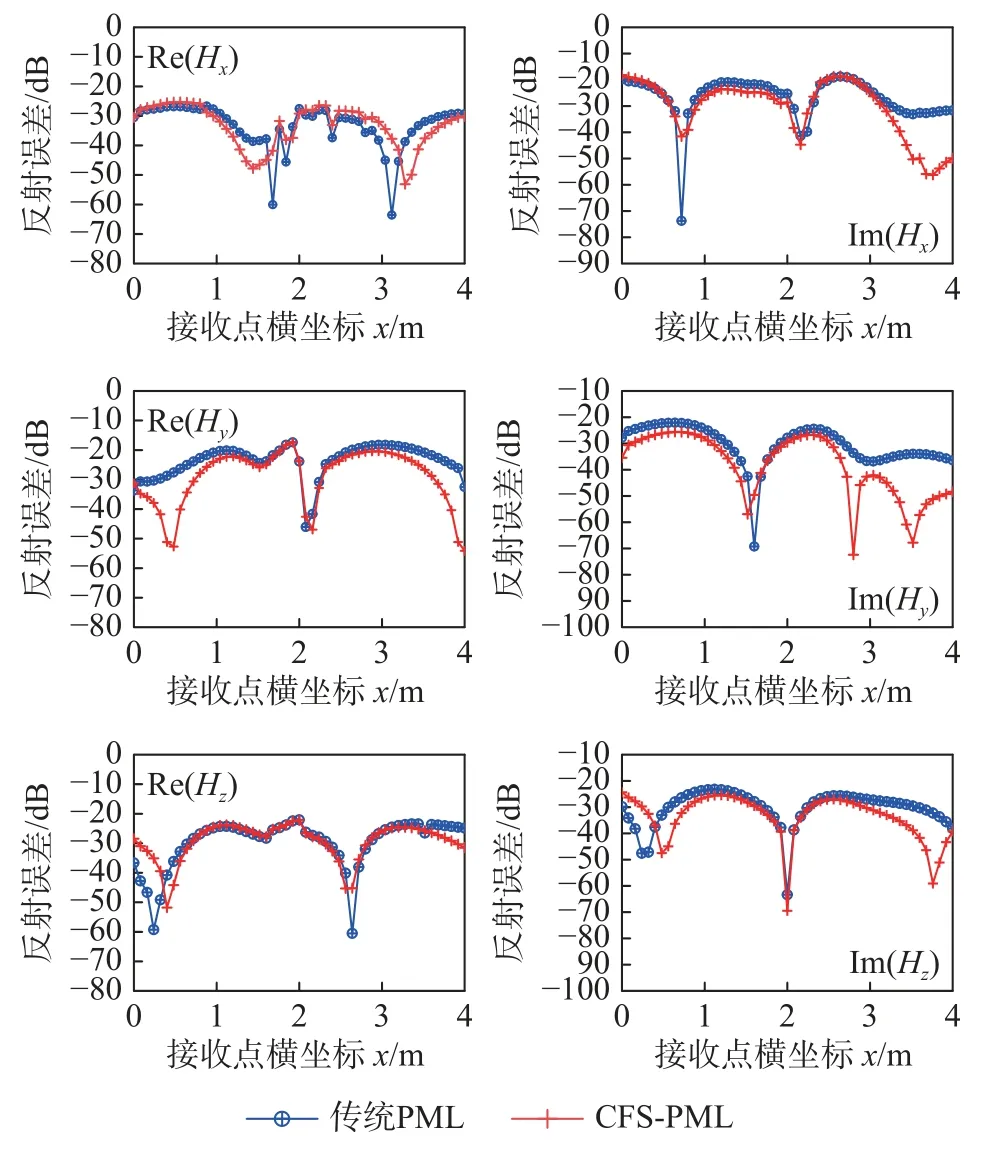
圖7 算例2 各接收點處磁場強度實部和虛部反射誤差對比Fig.7 Comparison of real and imaginary reflection errors of magnetic field intensity at each reception point(case 2)

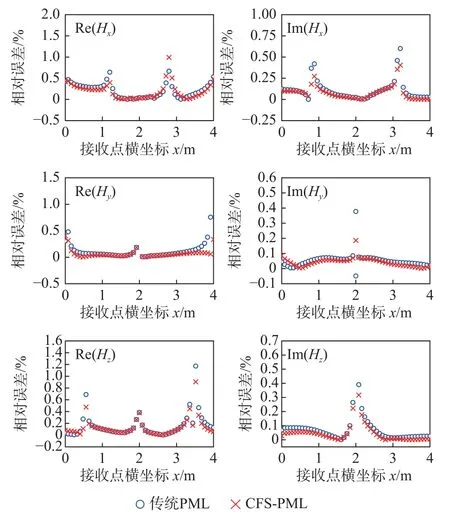
圖8 算例2 各接收點處磁場強度實部和虛部相對誤差對比Fig.8 Comparison of the relative errors of the real and imaginary parts of the magnetic field strength at each reception point(case 2)

3 結論

本文在頻域HO-FEM 算法的電磁場模擬中成功實現CFS-PML 人工邊界條件，極大地改善了PML 的吸收性能，提高了電磁場GPR 數值模擬的計算效率.與商業軟件WCT 數值模擬結果對比表明，CFSPML 邊界條件的應用具有更高的計算精度和效率，驗證了本文所提出算法的準確性和可靠性.兩個算例的數值結果表明至少能夠降低10 dB 的反射誤差，計算效率上分別提升17%、30%.

值得注意的是，本文公式推導僅考慮各向同性介質，并未考慮各向異性介質材料.此外，本文基于CFS-PML 的HO-FEM 并未采用加速并行等技術，以后這將成為我們研究的方向.