基于最小軌道交叉距離的小行星順訪探測目標預篩選方法

張佳文 鄭建華 李明濤

(中國科學院國家空間科學中心 北京 100190)

(中國科學院大學 北京 100049)

0 引言

一些深空探測任務為提高有效性，在完成主任務的轉移途中邊飛行邊探測，進行小天體多目標探測。例如，伽利略號（Galileo）衛星從地球轉移至木星途中順訪了小行星951 Gaspra 和243 Ida；嫦娥二號衛星在成功完成日地L2 點飛行探測后，對小行星4179 Toutatis 實現了飛越探測[1]。這類深空探測任務的軌道設計中，在主任務標稱軌道附近，一般通過軌道遞推求解探測器與小行星的相對距離來確定潛在探測目標[2-4]。

文獻[2]在伽利略號衛星軌道設計中，將小天體飛越探測目標搜索策略分為三步。第一步，針對4000 顆左右的小天體，分別計算其與探測器之間的相對距離，保留相對距離小于1.5×107km 的候選目標星。第二步，遍歷地球發射時間與木星到達時間，計算探測器與上一步篩選出的小天體之間距離最近時的時間與相對距離，選出可實現零距離或近零距離飛越的待選目標以及相應的地球發射時間和木星到達時間組合。第三步，針對待選目標星，將飛越小天體時間、距離、方位作為優化變量，對軌道進行重新優化設計。

文獻[3]對嫦娥二號衛星探測小行星目標的選擇主要分為三步。第一步，在小行星軌道特征和高精度軌道遞推模型基礎上，結合衛星壽命約束，選取近地小行星進行軌道遞推，搜索滿足2012 年10 月至2013 年6 月與地球最近距離小于1.5×107km 的目標。第二步，根據嫦娥二號衛星成像約束與潛在目標星的物理特征，確定小行星飛越探測的潛在備選目標。第三步，根據日–地–月系統轉移軌道兩點邊值問題的求解，通過分析潛在備選目標飛越探測的機會與速度增量，得到嫦娥二號衛星再拓展任務飛越探測目標小行星為4179 Toutatis。

文獻[4] 在得到2020—2025 年間向木星飛行燃料最省方案中較好的引力輔助序列為金星—地球—地球后，結合多任務探測，研究探測器在飛向木星途中穿越小行星主帶飛越探測小行星的軌道設計中，將探測器飛越小行星活動區域軌道段平均劃分，對276002 顆小行星計算在每一時間節點的位置，與探測器位置進行比對，統計二者相對距離小于可接近標準3×106km 的目標作為候選目標星，再從搜索結果中選擇飛越目標，重新設計軌道。

實際工作中，當探測器飛行軌跡范圍內的小行星數目龐大，并且標稱軌道弧段長時，直接通過軌道遞推的方式篩選目標計算量非常大。針對此問題，文獻[5] 在嫦娥二號探測小行星任務轉移軌道設計中，根據已編目小行星的軌道分布，首先基于近日距和遠日距篩選出地球軌道附近的小行星，作為進一步精確計算小行星目標的前提，再基于飛行任務約束選擇合適交會目標。這種預篩選方法對于地球附近的探測任務順訪小行星目標選擇效率的提升有效果，但對于飛往外太陽系的探測任務不適用。

因此，針對直接通過軌道遞推的方式來篩選目標計算量非常大的問題，本文提出在軌道遞推計算二者相對距離之前，基于小行星軌道的形狀和空間位置計算二者軌道在空間中的幾何最近距離，預篩選出滿足飛越探測距離約束的探測目標思路。研究中兩軌道在空間中幾何最近距離即最小軌道交叉距離（Minimum Orbital Intersection Distance，MOID），在Hedo 等[6]提出的求解兩橢圓軌道間MOID 的SDG（Space Dynamics Group）方法上進行改進，推導出可適用于雙曲線軌道的MOID 計算公式。依據此理論基礎，提出基于MOID 計算的小行星順訪探測目標預篩選方法，并以一條飛向日球層邊緣的深空探測任務軌道方案作為仿真算例。仿真結果證實了預篩選操作通過減少需要軌道遞推計算的小行星個數，降低了計算量，提高了順訪探測目標確定的效率[7]，并且由于MOID 計算公式對雙曲線軌道的適用性，此方法也適用于飛往外太陽系等復雜軌道類型的探測任務。

1 最小軌道交叉距離求解

最小軌道交叉距離，指兩天體密切軌道上最近兩點之間的距離。此問題的研究可用于預報具有潛在危險的小天體與地球發生碰撞事件[8]和計算空間碎片撞擊在軌航天器的概率[9]。

MOID 問題求解方法主要分為獲得距離函數所有臨界點的代數法[10-12]，迭代找到全局最小值的數值法[13,14]，以及代數與數值相結合的混合法[15]。文獻[10]通過求解軌道近點角為變量的經典三角方程，得到兩軌道間距離最小值；文獻[11]將尋找兩橢圓軌道間距離臨界點問題轉化為確定八次三角多項式的根的理論過程；文獻[12]應用幾何代數法搜索單變量16 次多項式實根，基于快速傅里葉變換給出兩軌道間距離臨界點。文獻[13]巧妙利用兩軌道間最小距離線的正交性迭代計算，評估小行星與行星間近距離接觸概率；文獻[14]提出一種快速的幾何方法，但是求解的準確性與計算速度成反比；文獻[15]采用一種主要通過在每個黃道子午面上一特定距離來近似軌道之間實際距離的數值方法，結合并行計算加快計算速度。

在上述研究背景下，2018 年Hedo 等[6]提出了SDG 方法，利用迭代法將空間內兩個橢圓軌道之間最近距離的求解轉化為求解其中一個橢圓上所有點與另一個橢圓之間的最近距離，可實現兩共焦點橢圓軌道MOID 的快速準確計算。針對兩個軌道中至少有一個軌道具有低偏心率的情況，Hedo 等[16]2020 年提出分別通過臨界偏近點角和平方距離的偏心率漸進展開式進行計算的方法。

到目前為止，包含雙曲線軌道組合的MOID 計算問題的相關研究工作較少，文獻[17]提出了通過查找距離函數所有駐點，即查找16 次代數多項式方程所有根的方法，但是由于程序原因，算法會帶來一定的數值誤差。

在深空探測任務中，探測器有沿雙曲線型軌道運動的情況。此時，雙曲線軌道與橢圓軌道之間的最近距離無法直接通過SDG 方法求得。鑒于SDG 方法中算法的靈活性，本文基于圓錐曲線運動模型改進SDG 方法，推導出雙曲線型軌道MOID 的計算公式。

1.1 橢圓形MOID 問題的SDG 方法

為便于描述，分別命名兩天體的橢圓軌道中一個為基準橢圓，另一個為次要橢圓，二者稱謂可互換。

SDG 方法可以概括為以下兩個算法[6]。

算法1 計算空間中任意點與基準橢圓之間的最近距離。

算法2 基于算法1，計算次要橢圓上所有點與基準橢圓之間的最近距離，集合中最小值即為所求MOID。

執行算法前，需要將次要橢圓上的點坐標變換到基準橢圓所在坐標系內，此過程涉及以下三類坐標系。

（1）慣性坐標系Fx0y0z0。以兩橢圓軌道公共焦點為坐標系原點，坐標軸滿足右手定則，[i0,j0,k0]為對應的單位矢量。經典的軌道根數（包括軌道傾角ij和 升交點經度Ωj以 及近點幅角ωj）是參考這個坐標系給出的，這里j=1 對應基準橢圓，j=2 對應次要橢圓。

（3）基準橢圓的中心坐標系Ox1y1z1。以基準橢圓的幾何中心為坐標系原點，坐標軸與基準橢圓軌道的近焦點坐標系Fp1q1h1坐標軸平行。二者定義以及相對位置關系如圖1 所示。

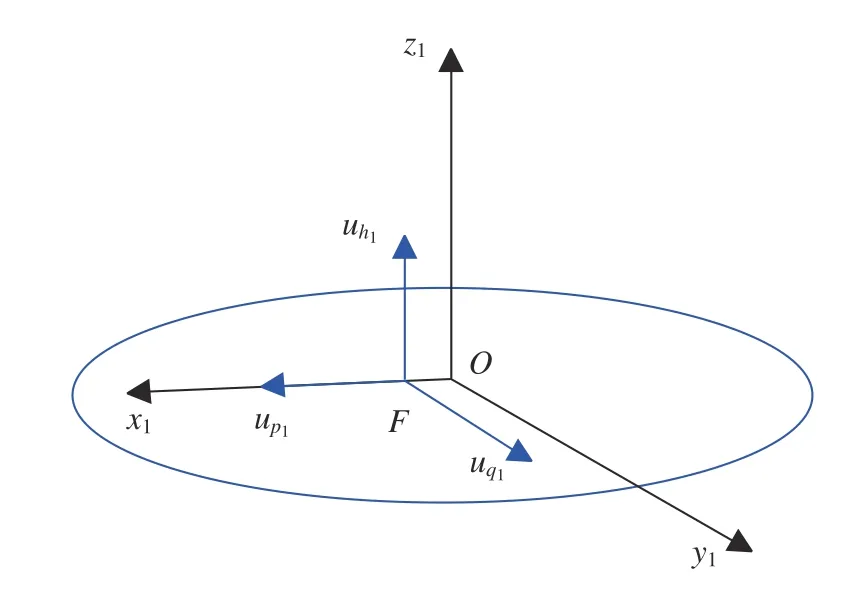
圖1 基準橢圓近焦點坐標系與中心坐標系的空間位置關系Fig. 1 Position relationship between perifocal reference and central frame of primary ellipse

其中，RZ(α)為 繞坐標軸Oz順時針旋轉α弧度的旋轉矩陣。

計算次要橢圓上的點E2與基準橢圓之間最近距離時，需將該點坐標轉換到基準橢圓中心坐標系Ox1y1z1中 ，點E2對 應的位置矢量可表示為OE2=F E2+OF，各個分量為式中，a1和e1分 別為基準橢圓的半長軸和偏心率；a2，e2，u2分 別為次要橢圓的半長軸、偏心率和點E2對應的偏近點角。

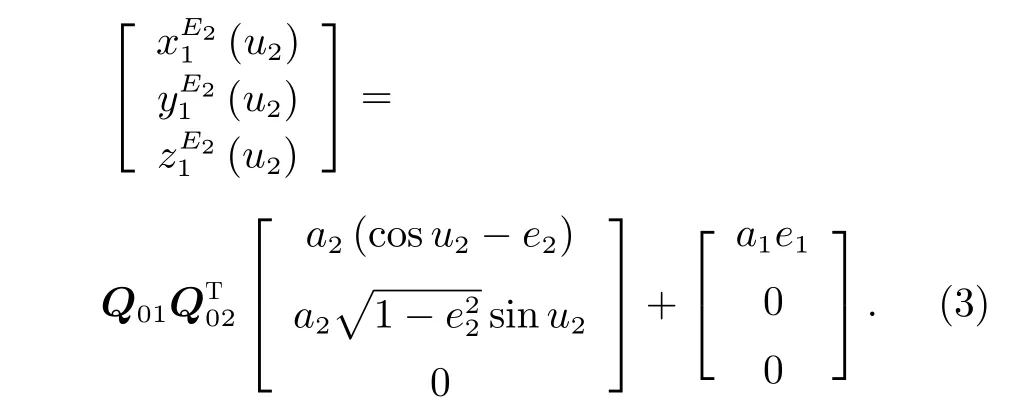
將空間中一點P0投影到基準橢圓所在平面，記投影點為P，則點P0到基準橢圓的距離被分解為兩個正交方向的分量，即點P0到點P的垂直距離和點P到基準橢圓的距離。對于給定的點P0，其與基準橢圓所在平面的垂直距離固定，因此點P0至基準橢圓的最近距離求解可轉化為投影點P至基準橢圓的最近距離求解問題。平面內一點與橢圓之間的距離如圖2 所示。

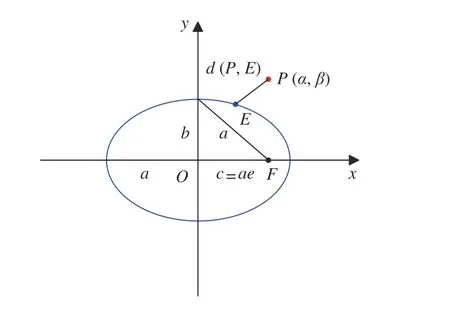
圖2 平面內一點與橢圓之間距離Fig. 2 In-plane distances between an ellipse and a coplanar point

在基準橢圓中心坐標系Ox1y1z1中，Ox軸、Oy軸分別與基準橢圓的長軸和短軸重合，基準橢圓關于Ox軸和Oy軸對稱。因此，求解投影點P與基準橢圓之間最近距離時，只對投影點P在第一象限的情況進行討論，落在其他象限的情況可根據橢圓對稱關系獲得。

用a，b，e分別表示基準橢圓的半長軸、半短軸和偏心率。用偏近點角u描述基準橢圓軌道上點E(x,y)的坐標，有式中滿足c=ae。

當基準橢圓為圓形，或者投影點P落在坐標軸Ox或Oy軸上時，距離極小值有解析解。表1 列出了這幾種特殊情況下的距離極小值解，表1 中xE′和yE′分 別表示距離為極小值dE′時對應的基準橢圓上點E′的橫縱坐標，uE′為該點的偏近點角。

表1 平面內一點與橢圓之間最近距離的封閉解情況Table 1 Cases of minimum distance between an ellipse and a coplanar point with closed-form solution

當投影點P落在第一象限內（α ＞0,β ＞0）時，極值條件式（6）沒有封閉解，需通過多項式求根或數值迭代法求解極值條件。在滿足求解精度情況下，數值迭代法的計算效率更高，迭代算法采用高度收斂的Halleys 方法[18]，迭代增量為

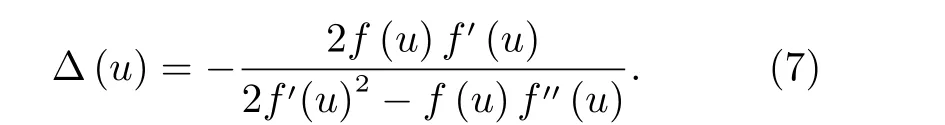
算法迭代計算的條件為

Δ(u)／=0?f(u)f′(u)／=0，迭代終止條件為

Δ(u)=0?f(u)f′(u)=0。f′(u′)=0f(u′)／=0u′

而當 ， 時，由于 不是方程的根，迭代不應停止，為避免此情況下迭代終止，增加判斷

1.2 雙曲線型MOID 問題的求解方法

鑒于SDG 方法應用場景的局限性以及求解方法的高效性，將該方法求解思路借鑒到雙曲線軌道MOID 求解中，針對不同的軌道類型，改進相應計算公式。

當基準軌道為橢圓而次要軌道為雙曲線時，雙曲線軌道上點H2坐標轉換到基準橢圓中心坐標系Ox1y1z1中 ，該點對應的位置矢量表示為OH2=F H2+OF，式（3）中各分量的表達式可以轉化為

當雙曲線軌道作為基準軌道時，SDG 方法的計算公式將不再適用，算法1 需要計算平面內點到達雙曲線（一支）的最近距離。

為描述方便，將基準天體雙曲線軌道稱為基準雙曲線，并認為基準雙曲線軌道位于左支，太陽位于左焦點，雙曲線軌道的定義如圖3 所示。

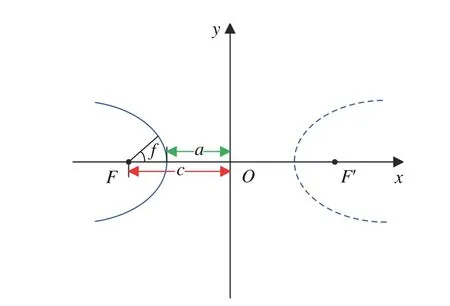
圖3 探測器相對于中心天體（焦點F）的雙曲線軌道Fig. 3 Hyperbolic orbit of the spacecraft relative to the central body ( focus F )

在此約定下，基準雙曲線中心坐標系Ox1y1z1中，次要橢圓上點E2的 位置矢量為OE2=F E2+OF，各分量為

基準雙曲線的對稱軸與中心坐標系的Ox軸平行，焦點F位于Ox軸負半軸，分別用a，b表示基準雙曲線的半長軸與半短軸。用偏近點角u表示基準雙曲線上點H(x,y)的坐標分量，有

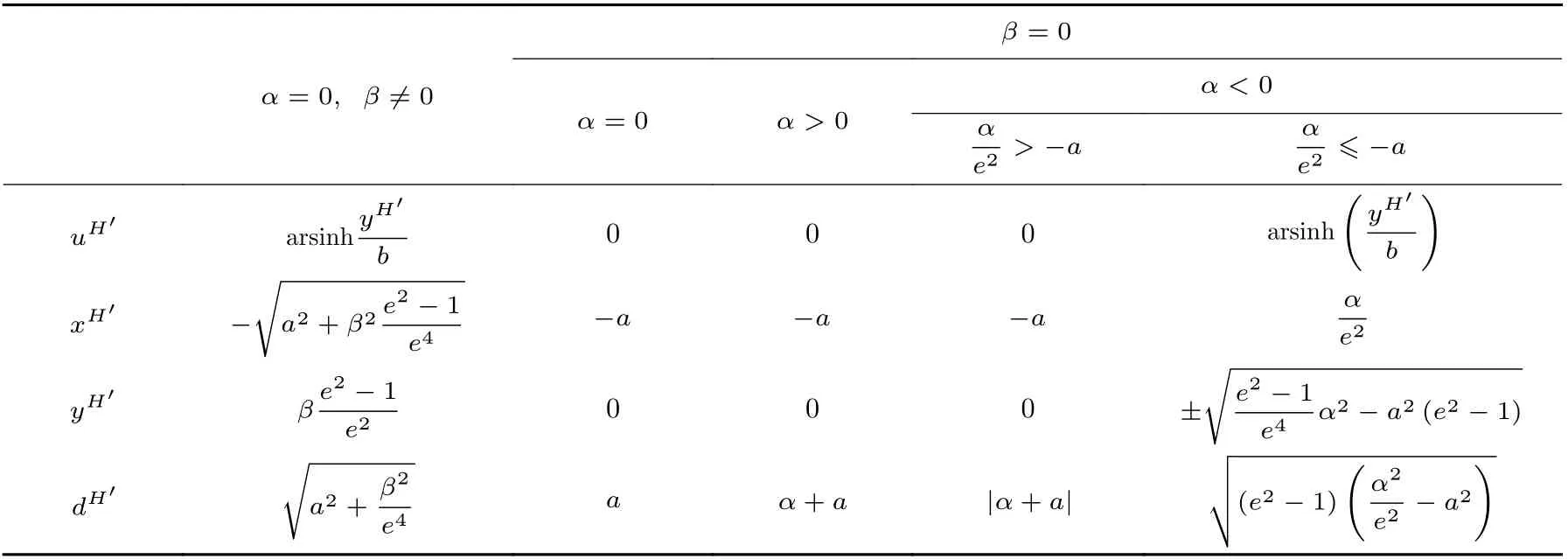
表2 平面內一點與雙曲線（左支）之間最近距離的封閉解情況Table 2 Cases of minimum distance between a hyperbola (left branch) and a coplanar point with closed-form solution

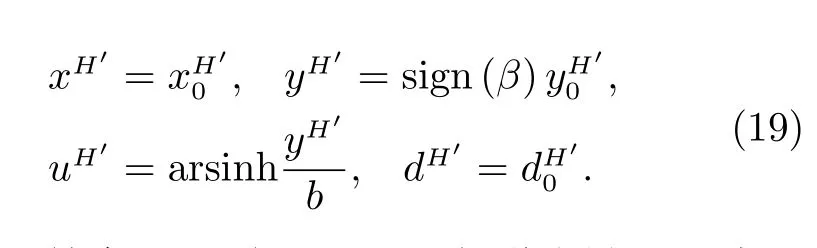
綜上，結合SDG 方法對基準軌道為橢圓的討論，以及本工作中針對基準軌道為雙曲線討論的兩種情況，可以實現對基準軌道類型為橢圓或雙曲線，次要軌道類型為橢圓或者雙曲線的MOID 問題進行快速準確求解。

1.3 結果驗證

文獻[19]可以對任意一對橢圓軌道之間的最小軌道交叉距離進行計算。為檢驗編寫程序的正確性與精確度，將計算結果與文獻[19]的結果進行比較。表3 中記錄了幾組軌道算例的結果，其中橢圓軌道根數依次為半長軸、偏心率、軌道傾角、升交點經度、近點幅角。半長軸單位為AU（Astronomical Unit），角度單位為度。為與本工作中的計算結果進行區分，將文獻[19]中MOID 結果標記為MOID 參考值。

表3 結果顯示，所編寫程序的計算結果與文獻[19]結果的誤差率不超過1.1×10–5%，可證實計算程序和算法的正確性。對于包含一條雙曲線軌道的MOID 計算，分別以該雙曲線軌道為次要軌道和基準軌道兩種方式進行計算，并將兩種計算結果列于表4。表3 和表4 中軌道根數的記錄順序為半長軸（單位AU）、偏心率、傾角（單位°）、升交點經度（單位°）、近點幅角（單位°）。表4 中結果驗證了求解雙曲線軌道MOID 計算公式的正確性與計算精度。

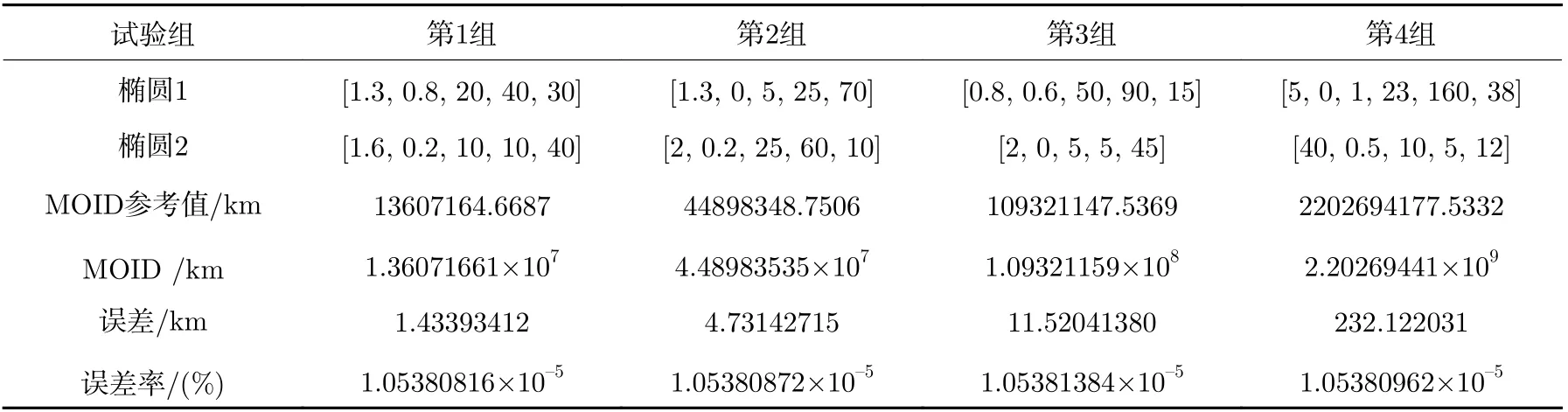
表3 橢圓軌道間MOID 計算結果Table 3 Calculation results of MOID between ellipses

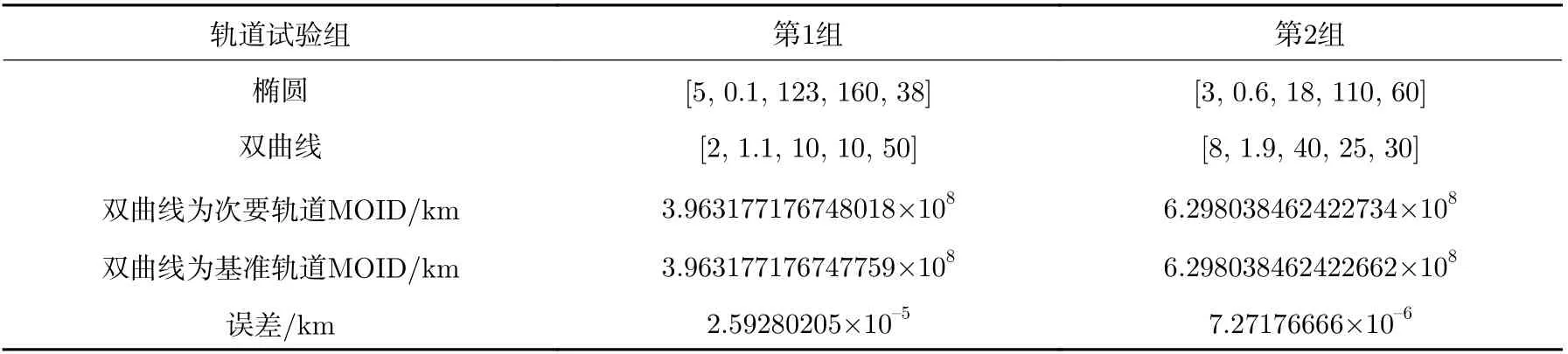
表4 橢圓軌道與雙曲線軌道間MOID 計算結果Table 4 Calculation results of MOID between ellipse and hyperbola

2 基于MOID 計算的小行星順訪探測目標預篩選方法

將空間內兩條軌道之間的最小軌道交叉距離應用到小行星順訪探測目標的預篩選問題中，計算小行星和探測器軌道之間的最小軌道交叉距離，與設定的可接近標準進行比較：如果MOID 大于可接近標準，說明二者相對距離大于順訪探測的距離要求，從探測目標群中淘汰該顆小行星；如果MOID 小于可接近標準，小行星和探測器之間可達到的真實最近距離可能滿足接近標準，需保留進行下一步軌道遞推求解二者相對距離。

由此，基于MOID 計算的小行星順訪探測目標確定可通過如下6 個步驟實現（見圖4）。

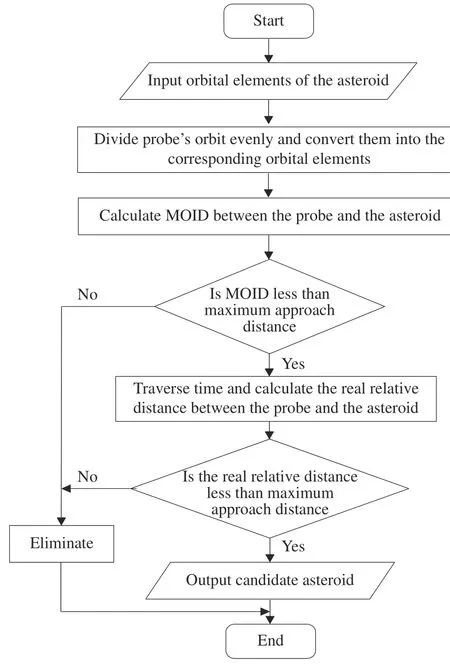
圖4 基于MOID 計算的小行星順訪探測目標篩選流程Fig. 4 Screening process of asteroid follow-up exploration targets based on MOID calculation

第一步 確定探測器飛越小行星活動區域的軌道與相應的飛行時間。

第二步 將探測器軌道平均劃分為n段，記節點時間為ti， 每一點的位置速度矢量分別記為r(ti)，v(ti)， 其中i=1,2,...,n。

第三步 由于探測器軌道可能是開普勒軌道與非開普勒軌道的組合，因此將每一節點的位置速度矢量轉為該點吻切軌道的軌道根數，以小行星軌道為基準軌道，探測器軌道為次要軌道，遍歷時間節點計算二者MOID 值，MOID 值集合中的最小值即為這一段探測器軌道與該顆小行星軌道之間的幾何最近距離。

第四步 對所有小行星進行第三步計算，保留幾何最近距離小于所設定可接近標準的小行星，完成預篩選過程。

第五步 對于從預篩選步驟中保留下來的小行星，通過軌道遞推計算每一時間節點上的位置矢量，記為rj(ti)，其中j為小行星編號。

第六步 判斷探測器與小行星的距離是否滿足設定的接近標準，如果滿足，則作為目標候選星，否則舍棄。

3 仿真算例

以一條2026 年發射飛往日球層邊緣的脈沖軌道作為仿真算例。探測器從地球逃逸后，經金星－地球－地球借力（Venus-Earth-Earth Gravity Assist，VEEGA）飛往木星，隨后經木星、海王星借力飛往日球層尾部方向（黃經為79°，黃緯為–5°）。針對探測器在海王星借力后飛至日球層邊緣[20]段軌道進行小行星順訪探測軌道設計，對應的小行星群體主要是位于海王星軌道之外的外海王星天體（Trans-Neptunian objects，TNO）。探測器整段軌跡的詳細參數列于表5。

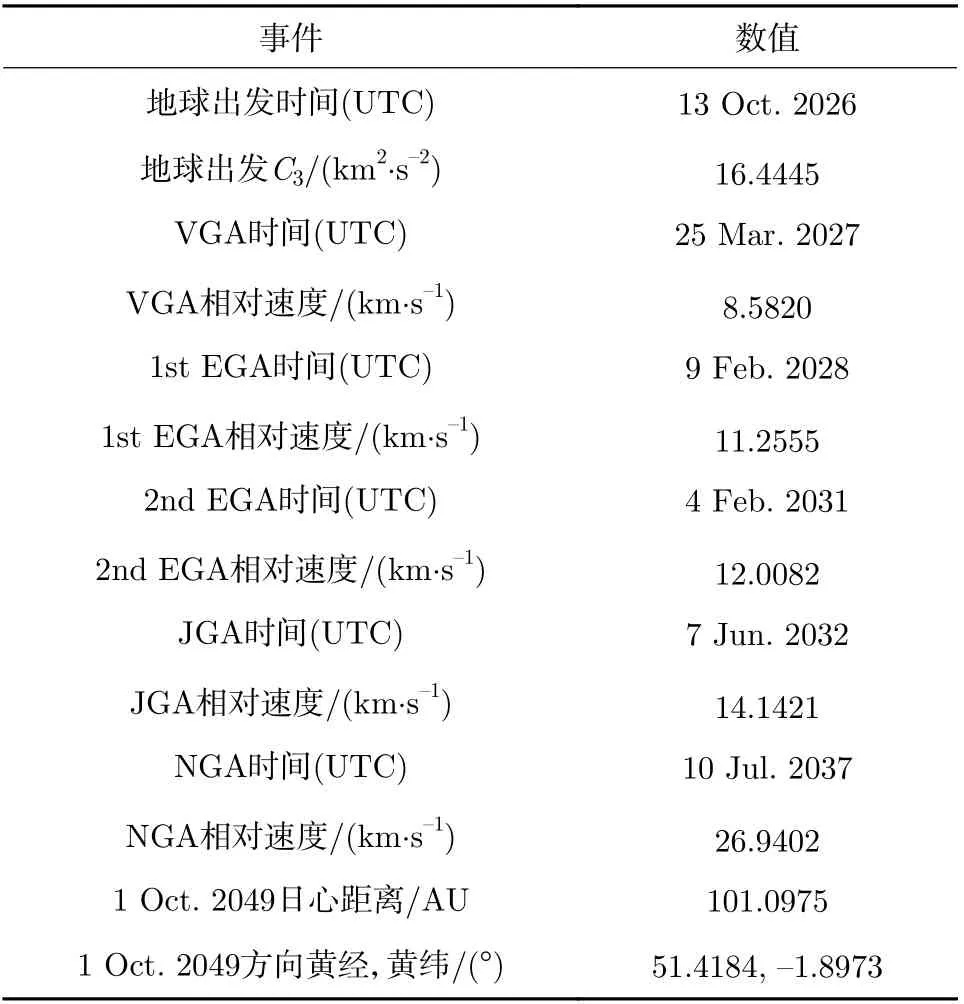
表5 仿真算例軌道詳細參數Table 5 Detailed parameters of simulation example

從國際天文聯合會（International Astronomical Union，IAU）的小天體中心（Minor Planet Center，MPC）網站[21]下載得到2503 顆外海王星天體的軌道數據，仿真中以太陽中心引力二體模型遞推計算小行星位置速度矢量[22]，在真實的太陽系動力學環境中，一些小行星（例如近地小行星、半人馬天體）所受攝動較大，簡單的二體模型可能導致小行星狀態計算有偏差[23]。為檢驗所提出小行星探測目標預篩選方法的效率與正確性，這里作此簡單處理，后續在進一步選擇探測目標、設計軌道方案時應對力學環境進行完整建模。探測器經海王星借力飛行近4500 天后距日心101 AU，針對此段軌道設置1 天的時間步長，標稱軌道被劃分為4467 個節點。仿真實驗的硬件環境為Intel(R) Core(TM) i7-5557 U CPU @ 3.10 GHz，8 GB 內存， 64 位IOS 系統。設置不同的小行星順訪探測可接近標準，分別用基于MOID 計算的目標預篩選方法和直接軌道遞推的傳統篩選方法進行計算，相應計算時間列于表6。

由表6 中結果可以看出，仿真算例中預篩選操作將計算時間大幅縮短，當可接近標準為2×108km 時，預篩選方法所需計算時間不到傳統方法計算時間的1/3，基于MOID 計算的小天體順訪探測目標預篩選操作有效提高了小天體探測目標確定效率。由于外太陽系空間尺度比較大，2×108km 的可接近標準在此任務軌道中是合理的，依此標準先篩選出部分目標，再微調軌道，最終可以實現消耗不多的速度增量近距離飛越小行星。表7 給出接近距離小于2×108km的小行星，圖5 為探測器接近小行星狀態。

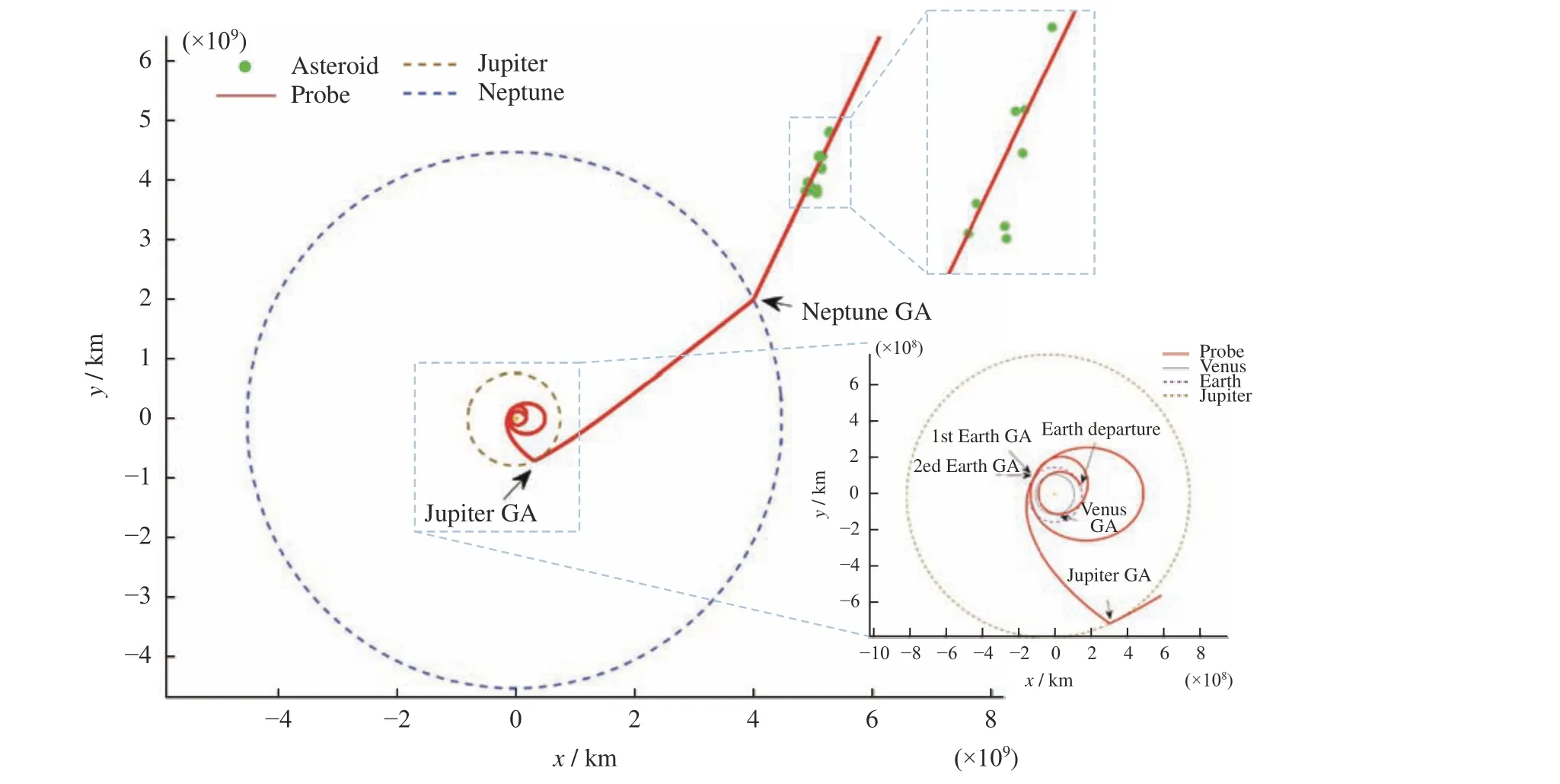
圖5 探測器飛越小行星搜索狀態Fig. 5 Search results of TNOs flyby

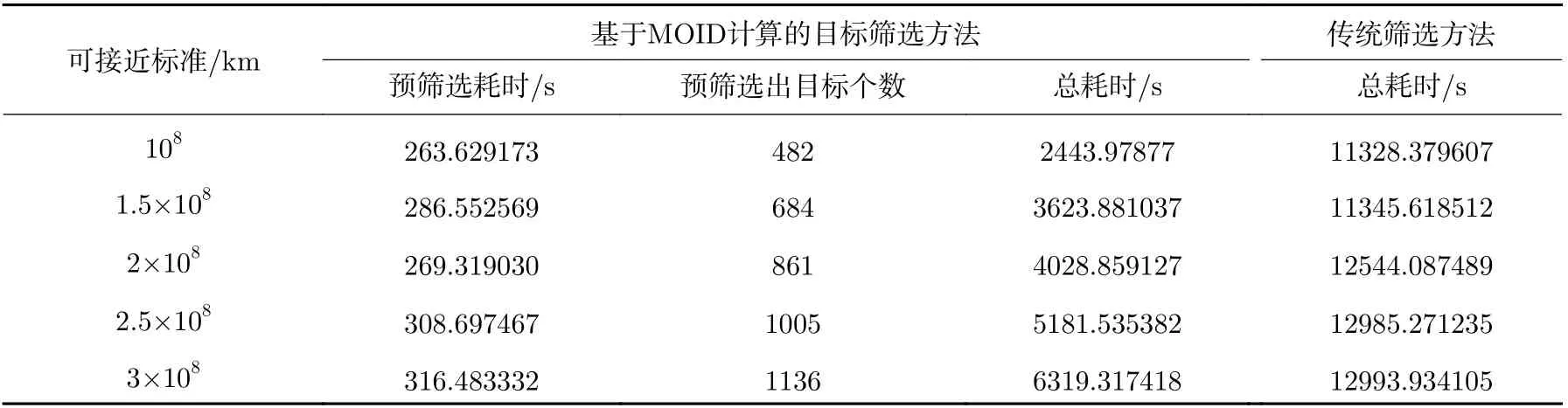
表6 小行星順訪探測目標篩選計算時間Table 6 Calculation time of asteroid follow-up exploration targets screening

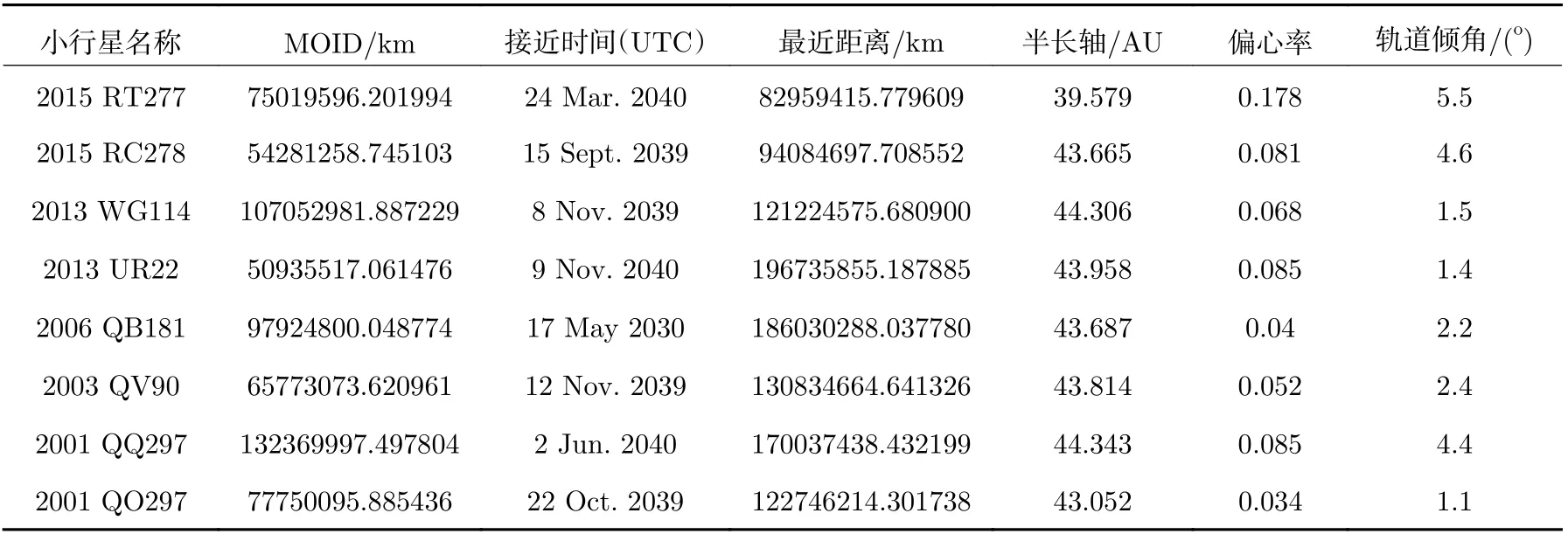
表7 接近距離小于2×108 km 的小行星Table 7 Approaching asteroids less than 2×108 km away

篩選得到飛越目標后，從搜索結果中選擇一顆或幾顆小行星作為飛越目標，重新優化設計探測器在海王星至日球層邊緣的飛行軌道。一般設計流程為：基于圓錐曲線拼接模型[24]進行軌道初步設計，在日心飛行段只考慮太陽引力，當探測器與行星日心位置相同時進行借力飛行[25]，與小行星日心位置相同時即認為飛越小行星；在軌道精確設計階段，以初步設計結果作為初值，考慮觀測、成像條件和探測器實際機動能力、受力情況及小行星真實力學環境等具體因素，詳細設計飛越小行星的軌道。

4 結 論

針對小行星順訪探測目標確定問題中，遍歷小行星和時間節點計算探測器與小行星之間最近距離時計算量大、效率低的缺點，推導了適用于雙曲線軌道最小軌道交叉距離計算的公式，提出了基于 MOID的小行星順訪探測目標預篩選方法，主要結論如下。

（1）雙曲線軌道MOID 計算公式的推導拓展了MOID 問題在軌道設計的應用場景。

（2）提出基于 MOID 計算的小行星順訪探測目標預篩選方法，減少了對整個小行星群體遍歷個體和時間節點求解探測器與小行星相對距離的計算量，節省了計算時間，提高了小行星順訪探測目標確定的效率。

（3）以一條運行近4500 天的標稱軌道為仿真算例，設置時間步長為1 天，從2503 顆外海王星天體中篩選順訪探測目標，當可接近標準設置為2×108km時，基于MOID 計算的預篩選方法耗時不到傳統方法計算時間的1/3。