VMD方法在旋轉機械振動信號處理中的研究*

駱東松 張樹濤

（蘭州理工大學電氣工程與信息工程學院 蘭州 730050）

1 引言

旋轉機械振動信號處理及診斷是檢測與識別機械故障的關鍵部分，旋轉機械設備運行狀態的特征信息主要從振動信號中可以提取，這些振動信號的正確處理和故障分析會影響旋轉設備的運行。不僅可以預測設備突然發生的故障，并且能夠降低設備故障引起的損失。在研究強復雜工作環境下微弱振動信號的采集時［1～4］，鑒于隨機共振系統參數由于預設不理想而經常處理效果不好的不足，提出了變分模態分解振動信號處理方法。本文采用VMD方法來解決傳統振動信號處理端點效應問題，將VMD算法添加到振動信號處理的算法過程中，通過對這些算法的研究，并可將VMD方法應用到旋轉機械振動信號的降噪處理及故障診斷分析中［5～9］。

2 VMD原理

變分模態分解（VMD）時把信號分解過程引入至變分模型中，采用“非遞歸”的方法，通過變分模型尋優的過程實現原信號的分解。當解決變分問題時，每個模態分量的中心頻率和帶寬被交替地迭代更新，最后獲得具有稀疏特征和準正交性的K個固有模態函數（IMF）［10］。VMD算法求解具體過程如下。

2.1 構造

VMD構造過程是在累積IMF與原始信號相等的條件下，求取各IMF帶寬之和最小值。求解過程如下。

1）進行希爾伯特變換獲得單邊信號頻譜；

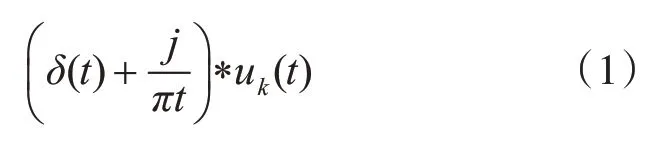
2）將各固有模態頻譜添加其預估的中心頻率ωk使固有模態頻譜移動至基頻帶；

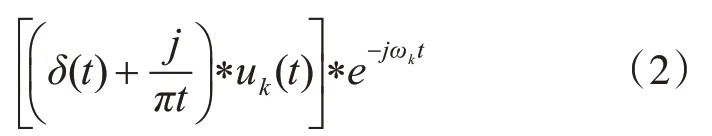
3）利用范數L2梯度的平方，求解各IMF帶寬得到約束性變分模型［11］；

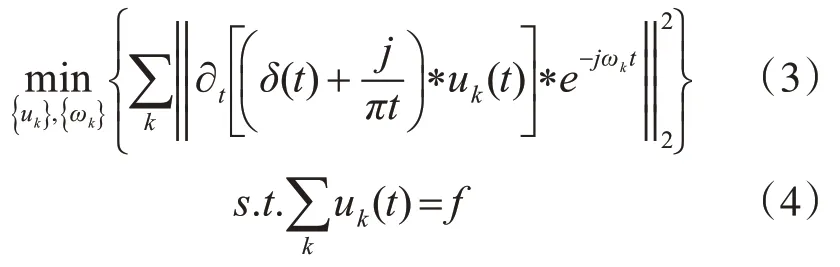
其中，{uk}={u1，u2，…，uk}表示K個模態函數的集合；{ωk}={ω1，ω2，…，ωk}表示K個中心頻率集合；δ(t)表示沖擊函數；*表示卷積運算。

4）將有約束的變分模型轉換為非約束變分模型［12］。

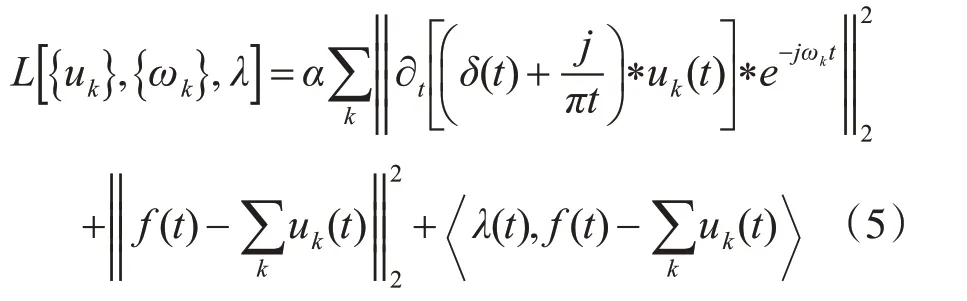
式中，α保證變分模型的收斂性，λ確保條件的約束力。

2.2 求解

VMD求解過程通過采用交替求解、、，求解增廣拉格朗日表達式的‘鞍點’，從而分解非約束變分模型，其實現過程如下。

2）由下式更新uk、ωk：

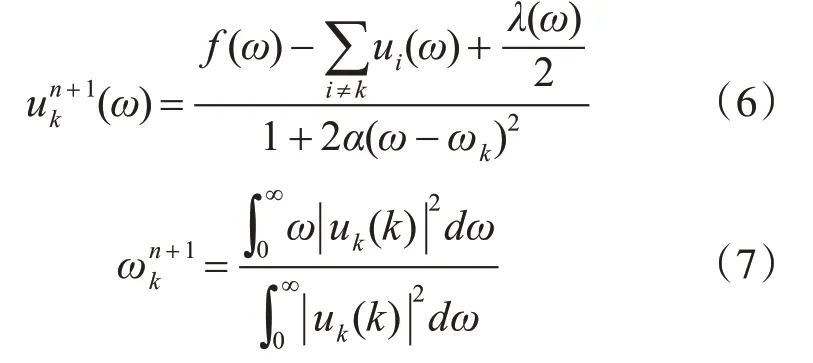
3）由式（8）更新λ：

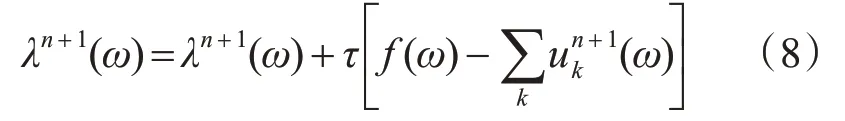
4）重復上述步驟式（2）、（3）直到滿足式（9）條件：

變分模態分解將復雜信號自適應地分解為若干個調幅調頻信號，制模態混疊現象。但是，懲罰因子α和分量個數K預設不好會直接影響處理效果。

3 VMD參數設定

3.1 K的確定

利用VMD算法提取信號特征時，傳統確定模態數K弊端在于工作量龐大，可靠性較低，而且需要大量的時間投入，因此，本文提出K值的確定方法：

1）選擇適當的K值，VMD可以避免由于混疊的相互影響而難以區分相鄰模式的情況，從而降低弱信號特征提取的難度。

2）保留原始信號的特征信息，而VMD分解應避免由于丟棄有用信息而導致的故障特征信息提取不完全，從而影響診斷效果。

因此，如式（10）和式（11）所示，分別給出了軸承和齒輪的模態數K的計算公式。

其中，Fs采樣頻率，Z為滾動體個數，fn為軸承故障特征頻率，fm為齒輪嚙合頻率。

根據香農采樣定理，分別可由式（10）和式（11）來估算出軸承和齒輪的可由式（10）估算VMD模態數K的值。

3.2 α的確定

VMD算法中α的取值也會直接影響到最終的分解結果，α的取值確保了在強噪聲干擾下信號的正常分解，α主要體現的是VMD分解的非線性和非凸性。1）當取的K值較小時：α的取值也較小時，會出現在VMD分解的過程中頻譜出現重疊現象，形成信息共享；當α的取值較大時，會出現在VMD分解的過程中頻譜信息的確實，采集到的振動信號特征信息不全。2）當取的K值較大時：如果α的取值也較小時，則模態分量信噪比將大大降低，分解出的頻譜中幅值較小的特征信息容易被平滑或減弱；如果α的取值較大時，分解的頻譜中較為重要的頻譜部分會出現重合現象，兩邊的弱譜很容易被覆蓋導致對于故障信息的錯誤分析。

因此，影響α的主要因素總結如下：

1）根據VMD分解后的結果表明，α的取值不能大于采樣的長度。

2）α確定VMD每種模式的頻率分辨率。VMD分解后，獲得的每個模態分量的離散點數為α，這將最終在相同采樣頻率的條件下影響每個模態譜線的頻率間隔。

所以，在確定好模態分解數K后，在樣本容量的范圍內將α的值從高調整至低，同時觀察不同值下的頻譜情況。在不丟失重要特征信號的頻譜前提下，α的取值越大，特征信號的頻率分辨率就越高，得到的結果越好。

3.3 τ的確定

不同的時間步長τ會對VMD分解產生不同的影響，在旋轉機械振動信號對于重構精度沒有特殊的要求時，可以取τ的值為0就可以達到效果，τ的值主要是確定乘法算子λ的更新，而λ是用來強制執行約束的變量，當τ=0時，λ將停止更新，VMD的分解結果更為理想。

4 VMD仿真分析

采用調幅調頻的多頻率疊加信號模擬存在多噪音振動信號進行仿真分析，模擬仿真如式（12）所示，選擇Fs為1000Hz，設置標準差為0.8，1000個采樣點的隨機噪聲。通過VMD方法對模擬含噪聲信號的分解過程，對比在模態混疊、端點效應以及抗干擾性等方面優劣。

模擬含噪信號仿真的時/頻域波形如圖1所示，由于選擇的模擬含噪信號較為簡單，因此噪聲幅值整體較小，從頻域波形圖中可以看到110Hz、145Hz、180Hz、205Hz的頻率分量。調幅調頻規律性明顯。

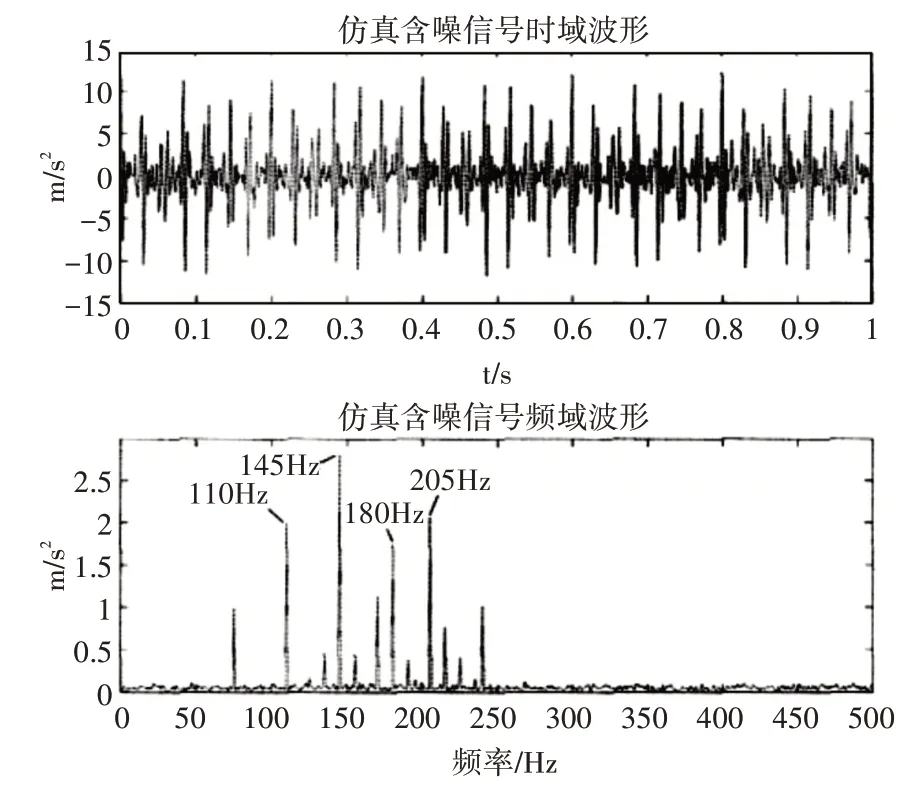
圖1 仿真信號時、頻域波形圖

根據前文的取值方式，分別取K=4、α=1000、τ=0，采用VMD算法進行對含噪模擬信號分解。仿真頻域圖結果如圖2所示。VMD方法根據信號頻率的高低將疊加頻率依次分開，圖中可直觀地看出頻率分別為110Hz、145Hz、180Hz、205Hz的分量，每個頻率所對應的是x1、x2、x3、x4分量疊加，從圖中可以看出分解結果明顯，無其他明顯混合噪聲。因此VMD算法能把振動信號中噪聲頻率相近成分分離，克服了傳統的端點效應問題和模態混疊問題［15～16］。

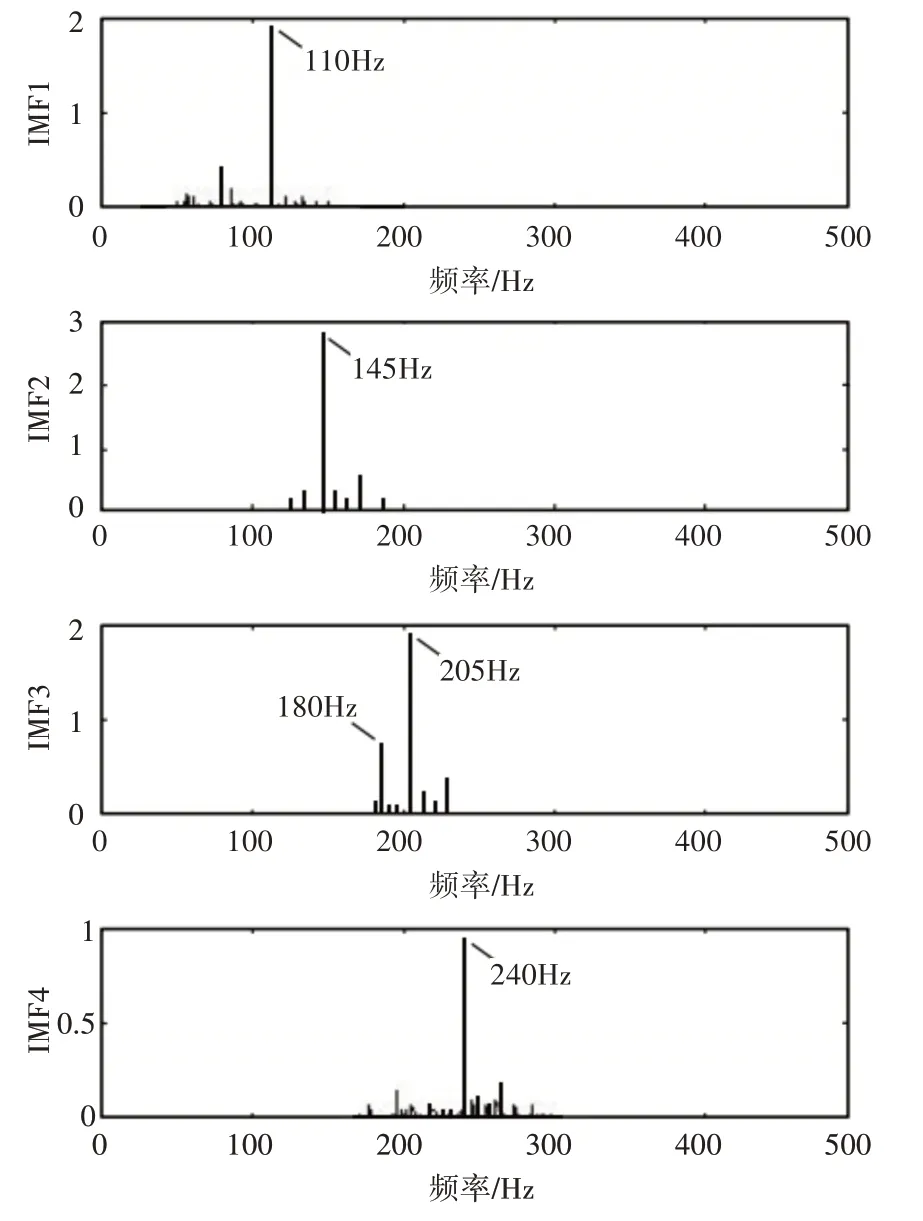
圖2 仿真信號VMD分解結果頻域圖

5 結語

本文采用VMW方法，彌補了傳統方法在旋轉機械振動信號處理中的不足之處，減少了傳統算法的工作量，提高了效率和可靠性。從VMD算法的基礎內容開始，通過對變分問題的構造和求解描述了VMD算法的基本原理，然后結合機械振動經驗分析過程對于參數K、α、τ進行優化，給出簡單取值的方法，最后通過取出的數值帶入相應的多頻疊加信號中進行VMD分解驗證，確定出算法的優越性。