基于MATLAB 的6R 機械臂運動學的仿真研究＊

胡宇航 張尚盈② 張曉艷

（①武漢工程大學機電工程學院，湖北 武漢 430205；②武漢譽瓊科技有限公司，湖北 武漢 430205）

近些年機械臂廣泛應用于多個生產領域，這是因為它使用方便、動作靈敏，并且能適應各種復雜多變的工作環境，能有效地減少勞動力、提高生產效率。在工業拆卸及大物件搬運等起重比要求高的環境中，大多使用液壓機械臂。

為了提高液壓機械臂的結構性能、作業精度等，其運動學的研究尤為重要。對于機械臂的建模及正逆運動學的研究方法選擇上，不論是D-H 建模還是其他的建模方式；數值解析法還是幾何法，或是神經網絡、遺傳算法求逆解，都各有利弊。大部分專家學者在進行對機械臂運動學的研究中都采取了不同的方法。對機械臂建模而言，郭發勇等[1]使用一種實體建模的方式（CFDH）使機器人建模更直觀準確，但建模步驟會繁瑣一些；Li F T 等[2]采用改進的D-H 法和幾何映射算法對液壓機械臂建模。對運動學分析而言，郭志強等[3]和趙修琪等[4]采用矩陣逆乘的方式求逆解，此過程易懂明了，但出現了漏解現象；張普行等[5]用空間幾何求反解，避免了大量矩陣乘和求矩陣逆；Peng J Q 等[6]對6 自由度機械臂劃分成兩個3 自由度，用解析法對其求逆解；黨浩明等[7]用中間變量替代齊次矩陣連乘，有效縮短逆解運算時間；Zarrin A 等[8]提出一種逆運動學的優化幾何解法，在笛卡爾坐標系下增加2 個角度輸入，增加機械臂工作空間，優化其效率，逆運動學求解大大降低了定位誤差；Duka A V 等[9]采用基于神經網絡方式求逆解，并對其軌跡進行跟蹤驗證，結果非常穩定。

本文以6R 液壓機械臂為研究對象，針對其正逆運動學進行研究和分析。首先，用改進的D-H 參數法構建機械臂運動學模型及正運動學方程，運用幾何法和解析法結合的方式求出運動學逆解，然后調用機器人工具箱對正逆解進行求解，分析對比計算值與真實值。最后，通過關節空間軌跡規劃進行仿真，驗證此建模及運動學分析的機械臂運動平穩有效，為之后運動規劃及實時控制打下堅實基礎[10]。

1 機械臂運動學分析

1.1 機械臂基本結構及建模

液壓機械臂是一款6R 關節串聯機械臂，其三維模型如圖1 所示，它的主要組成包括腰部（回轉）、大小臂（俯仰）以及手腕等部分，各相鄰桿件通過轉動關節連接，在工業拆卸、搬運等領域具有廣泛的應用。機械臂全液壓驅動，除肩部采用直線液壓缸、腕部旋轉采用液壓馬達，其余關節全部采用擺動液壓缸。

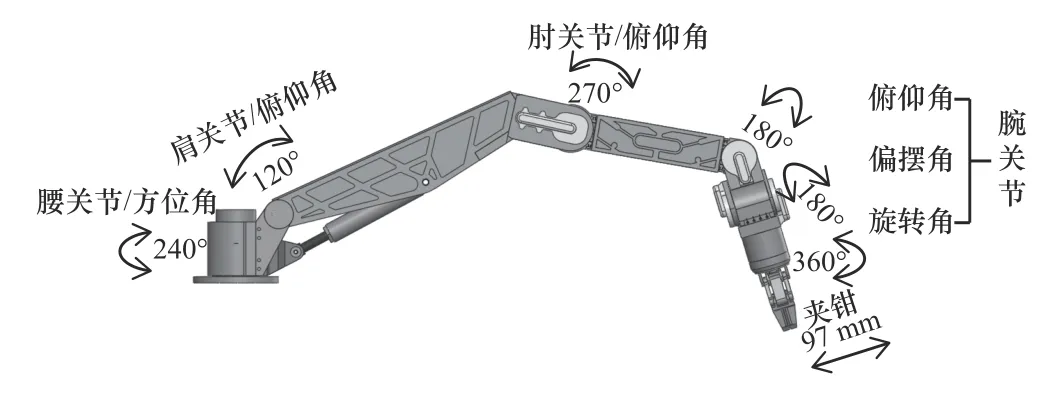
圖1 液壓機械臂三維模型

根據圖1、2 的機械臂三維模型及其尺寸參數，通過改進的D-H 參數法，建立機械臂坐標系，i-1系與i系之間的變換關系可以用平移和旋轉來表示。其建模的具體步驟如下：

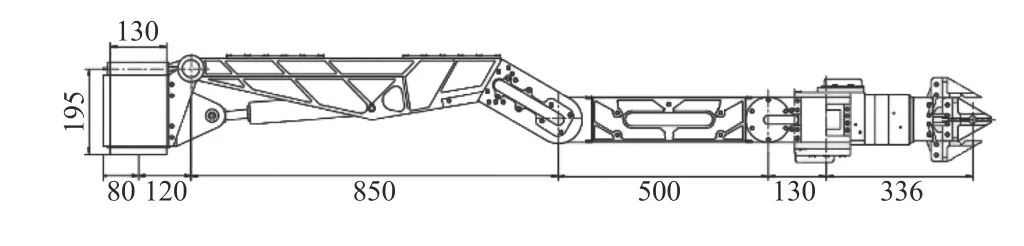
圖2 液壓機械臂平面尺寸

（1）令i-1系繞zi-1軸旋轉 θi，使xi-1與xi平行，其算子為Rot(zi-1,θi)。

（2）沿著zi-1軸平移di，使xi-1軸與xi軸重合，其算子為Trans(0,0,di)。

（3）沿著xi軸平移ai-1，使二者原點重合，其算子為Trans(ai-1,0,0)。

（4）沿著xi軸旋轉 αi-1，使得i-1系和i系重合，其算子為Rot(xi,αi-1)。

構建的機械臂坐標系簡圖如圖3 所示，構建的連桿參數及關節變量如表1 所示，其中 αi-1表示連桿坐標系之間的扭轉角度，θi表示各關節的旋轉角度，ai-1表示相鄰關節之間的連桿長度，di表示相鄰連桿之間的偏移量。在表中各參數之中，只有 θi為變值，ai-1、αi-1和di均為定值。

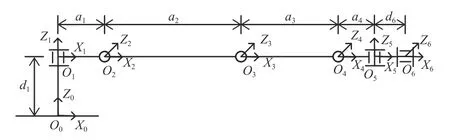
圖3 機械臂坐標系簡圖

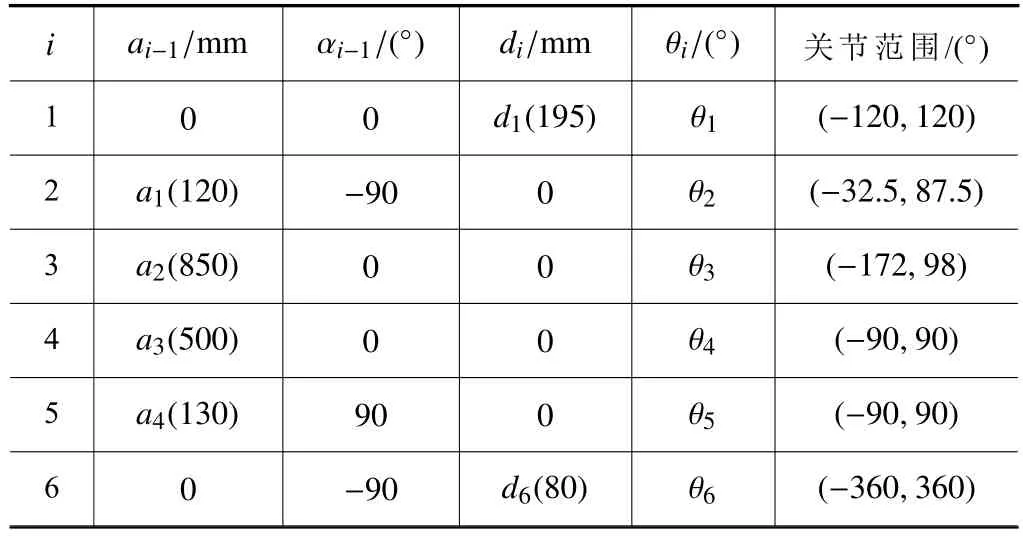
表1 液壓機械臂D-H 參數

1.2 機械臂運動學正解

機械臂的正運動學是通過兩連桿坐標系間的變換矩陣相乘得到末端位姿矩陣的過程。由于本文運用改進的D-H 參數法，其變換矩陣的通式用式（1）表示。

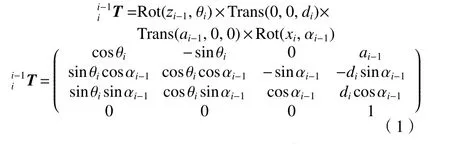
將表1 中各連桿的D-H 的4 個參數代入式（1）中，可依次得到如下各連桿變換矩陣。

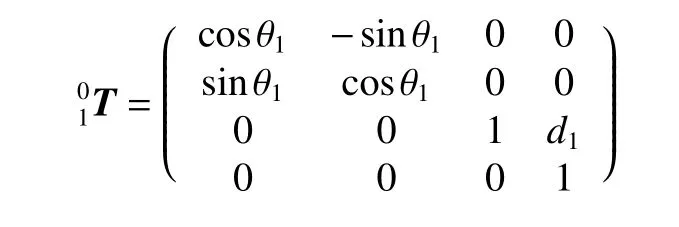
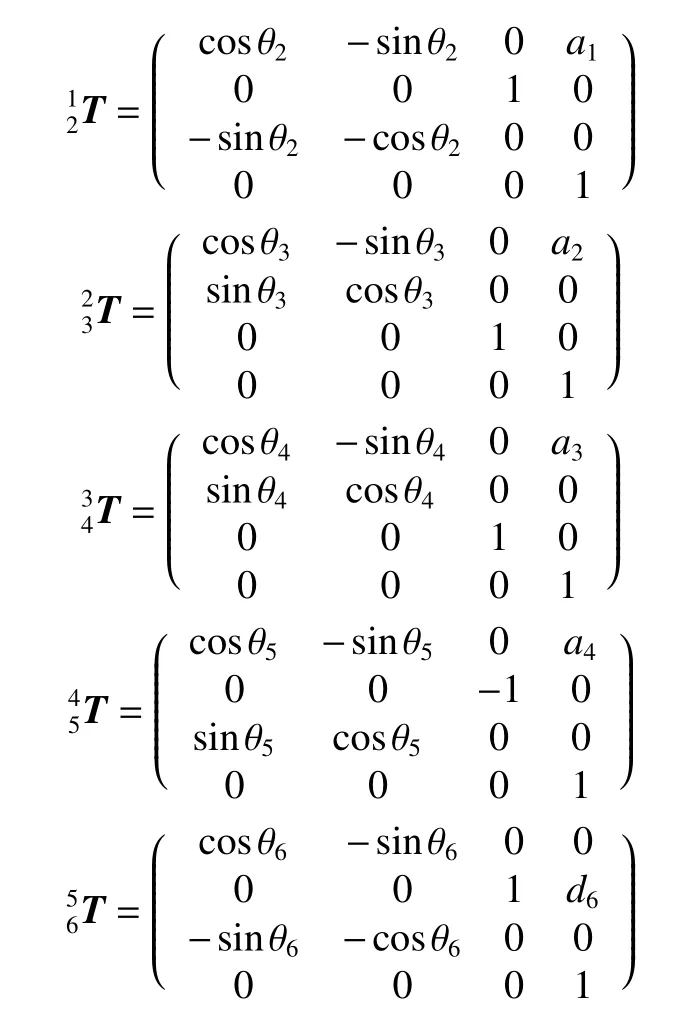
將以上各連桿變換矩陣依次相乘得到機械臂正解，如式（2）所示。

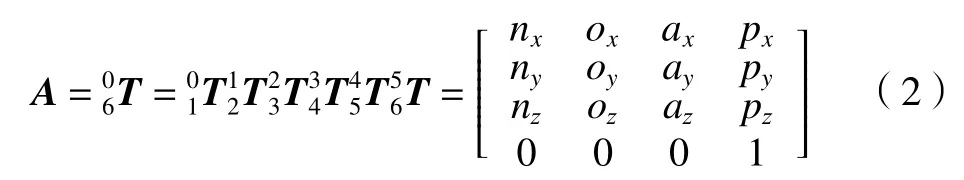
式（2）中：

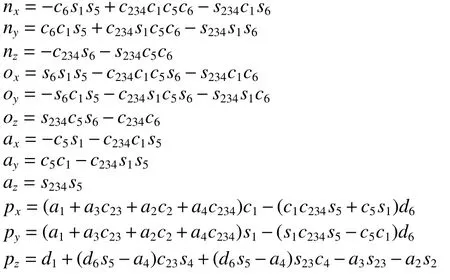
其中：c234=cos(θ2+θ3+θ4)，s234=sin(θ2+θ3+θ4)，c23=cos(θ2+θ3)。

1.3 機械臂運動學逆解

機械臂運動學求逆解是通過已知的末端位姿矩陣來求解各個關節的旋轉角度。求逆解的方法一般包括幾何法、解析法等。幾何法一般是將D-H 參數通過空間幾何轉換到平面上來求解；而解析法是通過變換矩陣得到的三角函數方程來求解。本文則通過幾何法和解析法結合的方式來求解機械臂運動學逆解，這樣可以大大減少其計算量。

（1）計算θ1,θ5,θ6

由于關節2～4 是俯仰關節，通過俯視角度觀其始終在一條直線上。關節5 為偏擺關節，關節6 為回轉關節連接在關節5 上，可知關節6 相對于關節5 的相對位姿是固定的。當給定末端位姿，可通過齊次變換得到關節5 相對于基座下的位姿，再通過圖4 就能確定 θ1的表達式。

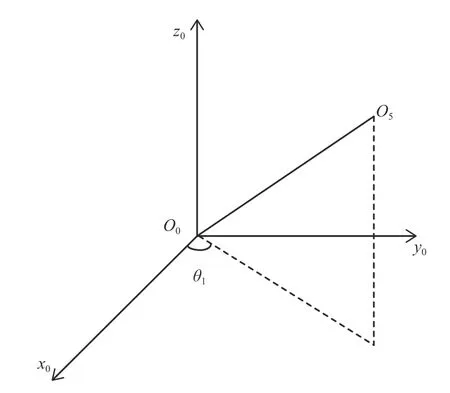
圖4 關節5 在基座坐標系下的投影

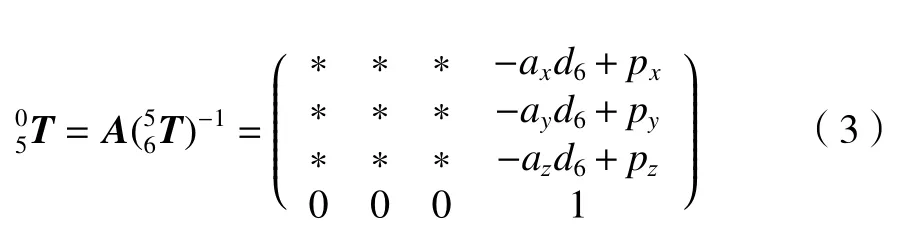
通過式（3）可得

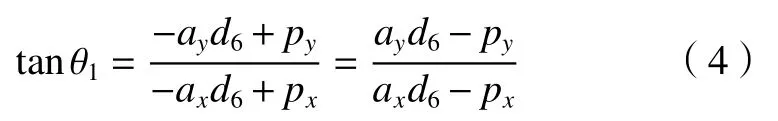
通過式（4）可得

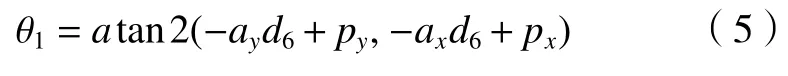
或

（2）計算θ2,θ3,θ4

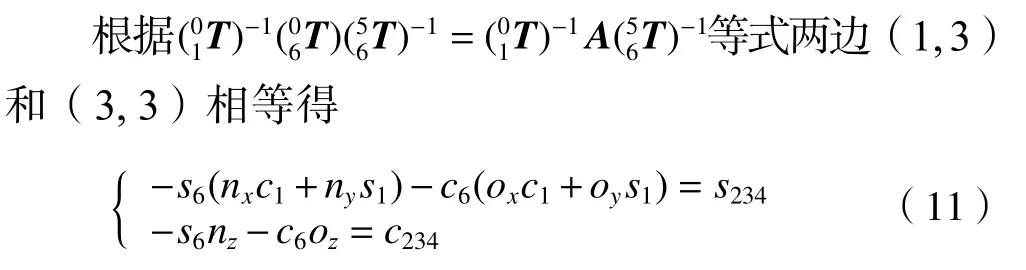
再根據（1,4）和（3,4）相等后移項得

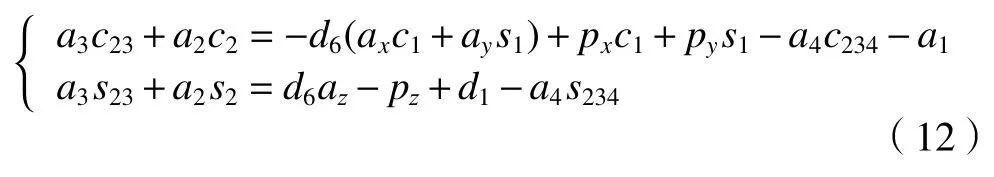
令X1和X2分別與式（12）右部分相等得

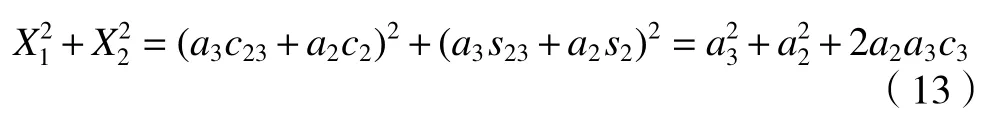
從而通過（13）求解θ3

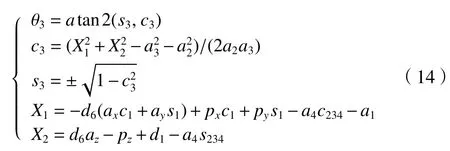
根據式（12）～（14）可求出θ2

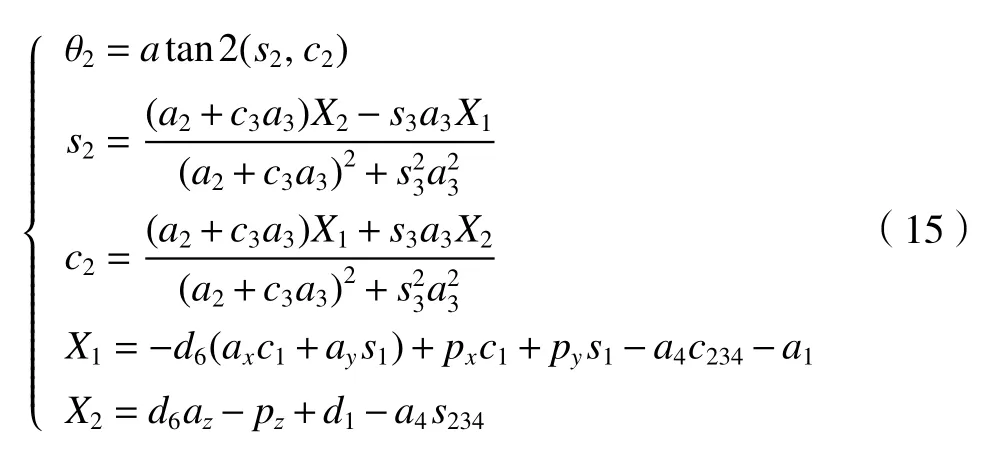
再根據式（13）～（15）可求出θ4

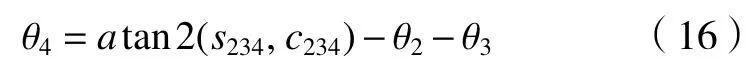
通過以上幾何法和解析法結合的方式已求出此液壓機械臂全部關節角，從以上各式可看出存在多解的情況，經過組合可生成8 組逆解，具體的求解流程如圖5 所示。大部分的機械臂都會存在多個逆解，會讓機械臂的末端位姿有多種選擇。但是在實際運動過程中，要充分考慮到機械臂參數的約束，會有部分逆解在機械臂可達空間之外，或是末端位姿不符合操作任務的要求，所以對求得的逆解需要進行驗證。

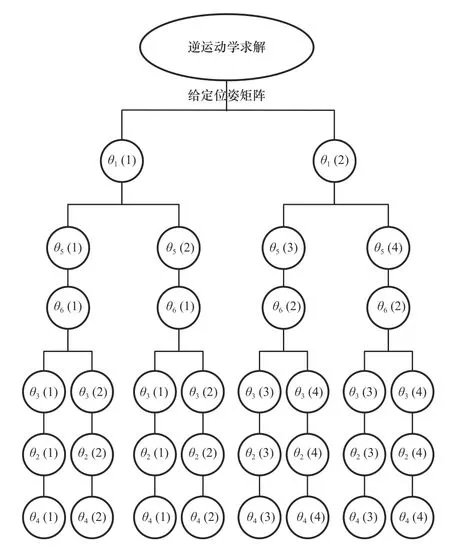
圖5 運動學求逆解流程圖

2 機械臂運動學仿真

2.1 建立運動學模型

在MATLAB 軟件中，使用機器人工具箱Robotics Toolbox 對機械臂進行運動學建模，它包含機器人所需要的多種運動學函數。根據表1 所給出的數據，運用機器人工具箱對機械臂建模，得到的初始模型如圖6 所示。

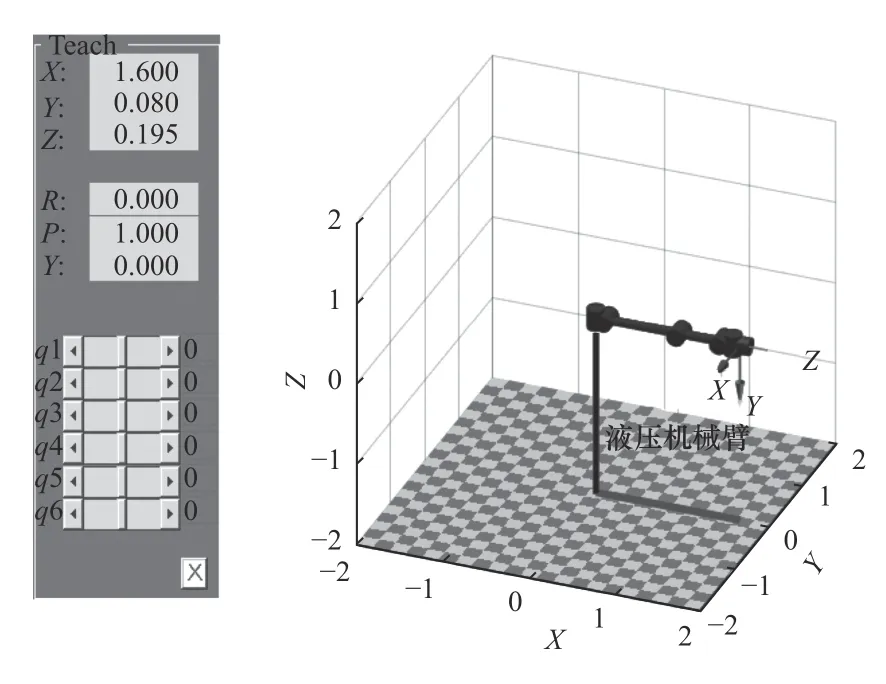
圖6 機械臂初始姿態

2.2 機械臂正運動學驗證

對機械臂進行正運動學的驗證，只需要將一組關節角代入式（10），得到的位姿矩陣與MATLAB得到的是否一致，若一樣則正運動學驗證正確。

取隨機一組關節角q1=[0 0 0 0 0 0]，代入到運動學正解公式中得到末端姿態矩陣T1，與機器人工具箱所得到的末端位姿矩陣（如圖6）一樣，驗證了機械臂正運動學方程與運動學模型的正確性。

2.3 機械臂逆運動學驗證

取q2=[30 60 45 75 45 120]*pi/180代入到機器人工具箱中進行求解，可得到末端位姿矩陣T2

將上述得到的位姿矩陣代入到（1.3）節中的計算公式，可計算出對應的運動學逆解。在MATLAB對機械臂逆解計算得出結果如表2 所示。

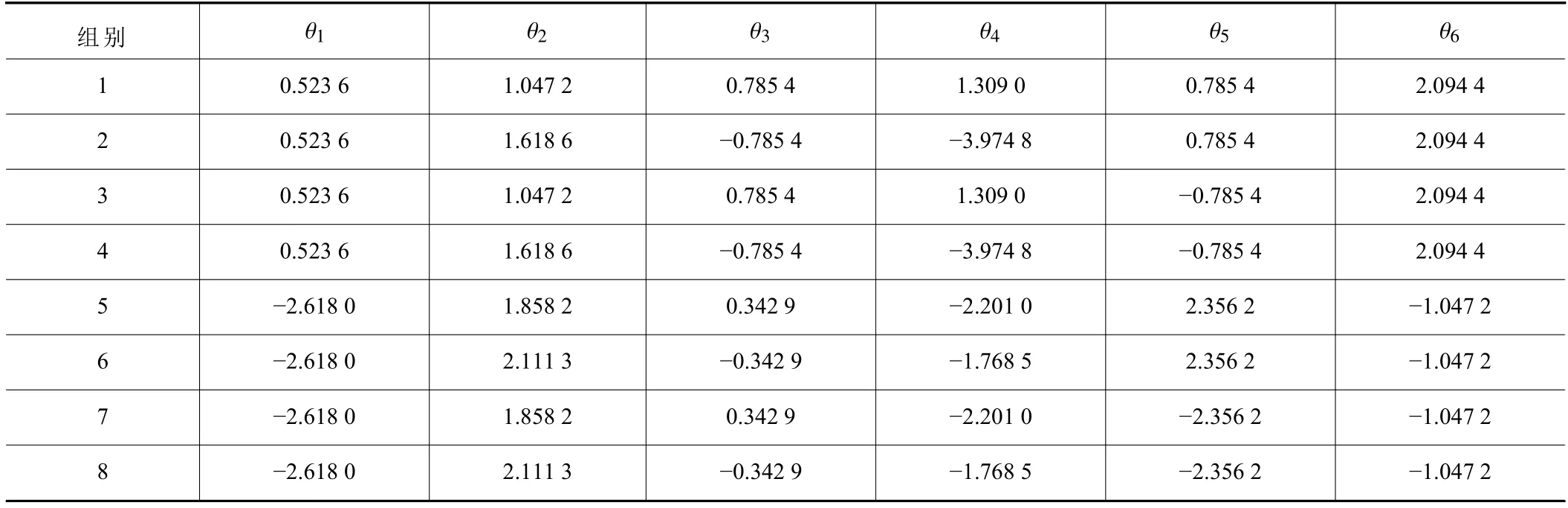
表2 運動學逆解數值

根據表2 的數據可知，對于每組末端位姿均可求出8 組逆解。當然在實際應用中，對機械臂的約束不同，機械臂能到達的關節角度只會是其中的一部分。經過數據對比，發現q2的取值與表2 第一組一致，至此驗證了建立此種逆運動學的正確性。

2.4 軌跡規劃及仿真

這里所指的軌跡規劃方法是指機械臂在運動時，對其位置、角速度及角加速度進行規劃，通過得到的曲線觀察其具體的運動狀態[11-12]。

選用關節空間軌跡規劃，在空間中選擇任意兩點，在機器人工具箱中調用函數對機械臂進行軌跡規劃。設關節空間中初始點所對應的關節轉角為q1=[0 0 0 0 00]，末端點所對應的關節轉角為q3=[45 -60 90 60 -36 -30]，得到的機械臂末端運動軌跡如圖7 所示。

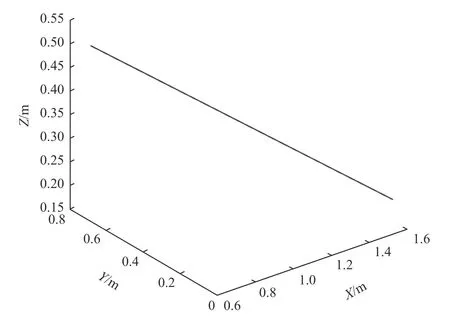
圖7 機械臂末端運動軌跡

需要對機械臂的6 個關節進行分析，分別對其位移、角速度及角加速度進行仿真。由圖8 可知，機械臂在運行過程中，6 個關節所有關節的角位移、角速度、角加速度隨時間變化曲線能平穩運行，不存在間斷和突變。由以上分析可知此液壓機械臂及末端執行器可連續平穩的完成作業任務。

圖8 液壓機械臂各關節仿真曲線

3 結語

本文以液壓機械臂為研究對象，基于改進D-H法對其進行運動學建模，建立正運動學方程。通過空間幾何法和數值解析法結合的方式求出其8 組逆解，在MATLAB 編寫程序驗證了正逆運動學的正確性。借助機器人工具箱，在關節空間中進行機械臂運動軌跡的仿真，通過觀察各關節角位移、角速度和角加速度的平滑曲線，驗證了機械臂參數的合理性。