兩有限熱源間的不可逆磁Ericsson制冷循環的優化分析

葉興梅，張麗敏，方玉宏，陳景東

(閩南師范大學物理與信息工程學院，福建 漳州 363000)

0 引言

磁制冷是一種先進制冷技術，具有高效節能、綠色環保和結構緊湊等優越特性[1-2]，因而關于磁制冷的研究成為低溫技術領域非常活躍的一個課題。磁Ericsson制冷循環因其制冷溫區寬、易控制等優點備受青睞。一些學者應用有限時間熱力學理論對其進行研究，得到一些有意義的結論。例如，嚴子浚和楊惠山[3-4]研究熱阻、非理想回熱和回熱時間對磁Ericsson制冷機性能的影響，導出Ericsson制冷循環的基本優化關系。張燕燕[5]研究了一般傳熱規律下的磁Ericsson制冷機的優化性能，探討熱阻和非理想回熱對一類磁Ericsson制冷機的影響。袁都奇[6]建立了受熱漏、熱阻及回熱損失等主要不可逆因素影響的順磁質Ericsson 制冷循環模型，分析各種不可逆性對Ericsson制冷循環性能影響的本質差異。莊小玲等[7]應用Langevin函數的近似式以及熱力學分析方法，揭示有限速率熱傳導、不平衡回熱、回熱器效率及熱漏等對鐵磁Ericsson制冷循環性能的影響。徐志超等[8]據朗之萬理論導出鐵磁材料的磁化強度和熵表式，揭示有限熱源、回熱器效率、外磁場強度等參量對磁Ericsson制冷循環熱經濟及相應的熱力學性能的定量影響。XIA等[9]探討了熱阻、非理想回熱、回熱器損失、熱漏及工質內部不可逆耗散等對磁Ericsson制冷循環性能的影響。YE等[10]建立了受外部熱源有限熱容、熱阻、固有回熱損失、附加回熱損失和工質內不可逆等影響的磁Ericsson 制冷循環模型，導出制冷率和制冷系數及制冷率與輸入功率間的優化關系。在磁Ericsson制冷循環的進一步研究中，有必要更全面地考慮各種不可逆因素對制冷機性能的影響。為此，本文建立以滿足居里定律的順磁質為工質的Ericsson制冷循環新模型，綜合考慮熱源熱容量有限、熱阻、非理想回熱、回熱器損失、熱漏及工質內不可逆性等不可逆因素，分析各種不可逆因素對制冷循環制冷率和制冷系數的影響。

1 順磁材料的主要熱力學性質

理想順磁質的磁化強度M可用布里淵函數BJ(x)表示，即

M=ngμBJBJ(x),x=gμBJH/(kT)，

(1)

其中，n為單位體積順磁質的原子或離子數，g為朗德因子，μB為玻爾磁子，J為角動量量子數，H為磁場強度，k為玻耳茲曼常數，T為絕對溫度。

當x?1時，布里淵函數為

(2)

在這種情況下，(1)式可簡化為

(3)

(3)式就是熟知的居里定律，其中，C為居里常數。

根據(3)式并忽略順磁質的體積變化，應用順磁質的熱力學基本方程可推出滿足居里定律的順磁質的熵為

(4)

其中，S0(T)僅是溫度的函數，μ0為真空磁導率。

再由(4)式可得，順磁鹽的等磁化強度熱容CM僅是溫度的函數，而等磁場強度熱容

(5)

不僅是溫度T的函數，還與磁場強度H相關。

許多順磁鹽在溫度低于1 K時居里定律還相當準確，甚至有些在0.01 K以下時仍可適用[3]，而磁Ericsson制冷循環大多用于20 K以上的溫區。所以本文基于居里定律對順磁質Ericsson制冷循環進行優化分析，所得到的結論具有較大的適用范圍。

2 不可逆磁Ericsson制冷循環

不可逆磁Ericsson制冷循環模型如圖1所示，工質進行兩個等溫和兩個等磁場強度過程。

圖1 不可逆磁Ericsson制冷循環T-H圖

在圖1中，過程a→b表示溫度為T1的等溫磁化過程，磁場強度由H1升到H2，同時工質放出熱量Q1致使變溫高溫熱源的溫度從TH1上升到TH2；過程b→c表示H=H2的等磁場強度過程，溫度由T1降至T2，并向回熱器放出熱量Qbc；過程c→d表示溫度為T2的等溫去磁過程，磁場強度由H2降至H1，在此過程工質吸收熱量Q2使得變溫低溫熱源的溫度從TL1下降到TL2；過程d→a表示H=H1的等磁場強度過程，溫度由T2升到T1，并從回熱器吸收熱量Qda。根據對數平均溫差法[10-11]，則有

(6)

(7)

本文的磁Ericsson制冷循環以遵從居里定律的順磁鹽為工質，則由(4)(5)式得到的工質與高、低溫熱源及回熱器交換的熱量可分別表示為

(8)

(9)

(10)

(11)

由于H2>H1，從(10)(11)式可知，Qbc>Qda，即回熱器吸收的熱量大于從回熱器放出的熱量，因此以單一順磁鹽為工質的Ericsson制冷循環不具有理想回熱的條件[3]。由于回熱器經一循環后要恢復原狀，否則無法維持正常的工作。因此，回熱器中多余的熱量

(12)

必須及時地釋放到低溫熱源去，這樣就造成了非理想回熱。

由于有限速率熱交換，回熱器的回熱損失不能忽視，假設由此引起的附加回熱損失正比于非理想回熱Qr，即可表示為

ΔQr=(1-ηr)Qr,

(13)

其中，ηr為回熱器的回熱效率，ηr≤1。

回熱過程也需要一定的時間，設兩個等磁場過程進行的時間為[10]

(14)

其中，γ為與溫度無關的常數。

考慮到高低溫熱源之間存在熱漏，假設每循環從高溫熱源到低溫熱源的熱漏損失為[6]

QL=qlτ,

(15)

其中，ql為熱漏率；τ為循環周期，τ=t1+t2+t3+t4。

進一步，考慮到磁工質在制冷循環過程中不可避免地存在渦流等耗散，使得工質內部存在不可逆性，為了定量描述這種內不可逆性，引入內不可逆因子：

(16)

3 制冷率和制冷系數的數學表達式

聯立(6)至(16)式，可求得每循環的凈放熱量和凈制冷量為

QH=Q1-ΔQr-QL,

(17)

QC=Q2I-1-ΔQr-Qr-QL.

(18)

進而得到制冷率和制冷系數表達式分別為

(19)

(20)

其中，y為兩等溫過程的溫度比，

將(19)式代入極值條件?R/?T2=0可求得

T2=(bTH1+TL1)/(1+by),

(21)

再將(21)式代入(19)(20)式，可得到制冷率和制冷系數數學表達式分別為

R=kHTL1(yI-1-A1(y-1))((1+by)2/(y-TH1/TL1)+B(y-1))-1-ql,

(22)

(23)

其中，B=kHA2TL1。

利用(22)(23)式，可進一步定量分析回熱效率、內不可逆因子、磁場強度、熱漏率以及高、低溫端熱交換因子對不可逆磁Ericsson制冷循環性能參數的影響。

4 討論

4.1 優化的工作區域

I=1.05；ηr=0.95；εH=εL=0.9；ql/(CLTL1)=0.000 5；B=10。圖2 溫度比對制冷率和制冷系數的影響

4.2 高、低溫端熱交換器有效因子對循環性能的影響

I=1.05；ηr=0.95；ql/(CLTL1)=0.000 5；B=10。圖3 高、低溫端熱交換有效因子對R*～ε曲線的影響

表1 高、低溫端熱交換有效因子對制冷機4個重要性能參數的影響

4.3 內不可逆因子和回熱器效率對循環性能的影響

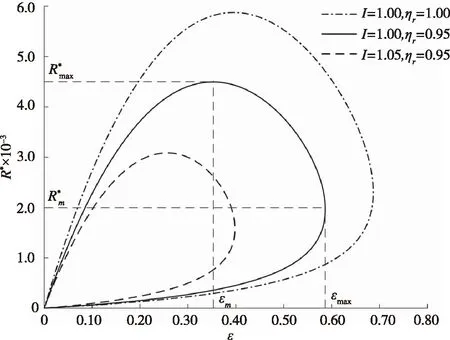
εH=εL=0.9；ql/(CLTL1)=0.000 5；B=10。圖4 內不可逆因子和回熱器效率對R*～ε曲線的影響

表2 內不可逆因子和回熱器效率對制冷機4個重要性能參數的影響

4.4 熱漏對循環性能的影響

εH=εL=0.9；I=1.05；ηr=0.95；B=10。圖5 熱漏對R*～ε曲線的影響

4.5 磁場強度比對循環性能的影響

εH=εL=0.9；I=1.05；ηr=0.95；ql/(CLTL1)=0.000 5；4μ0γkHTL1/C=120 T2；μ0H1=2 T。圖6 磁場強度比對R*～ε曲線的影響

4.6 特例

當外部熱源的熱容量為無限大，且忽略內不可逆性和熱漏時，即當CH,CL→∞，I=1，ql=0，由(22)(23)可得：

(24)

5 結語

本文建立了包含有限熱源、熱阻、非理想回熱、回熱器損失、工質內不可逆性和熱漏等不可逆因素在內的磁Ericsson制冷循環，應用對數平均溫差法和最優控制理論，導出了制冷率和制冷系數的具體表達式。通過數值算例和圖形詳細分析了高、低溫端熱交換器的有效因子、內不可逆性和回熱器效率、熱漏率和磁場強度比對磁Ericsson制冷循環性能的影響。研究結果表明，磁Ericsson制冷循環的制冷率和制冷系數隨著高、低溫端熱交換器有效因子的增大而增大，制冷率的增幅大于制冷系數；當內不可逆因子增大或回熱器效率降低時，制冷率和制冷系數都顯著減小；當熱漏不為零時，制冷率與制冷系數之間的優化關系曲線為扭葉形，熱漏增大，最大制冷系數所對應的無量綱制冷率增大，而其他三個性能參數隨之減小；當磁場強度H1給定，磁場強度比越大，循環優化區域越寬。綜上所述，盡可能提高回熱器效率和磁場強度比以及高、低溫熱交換有效因子，減小內不可逆因子和熱漏對不可逆磁Ericsson循環性能是大有益處的。