基于CFD的變后掠翼單速度最優后掠角預測模型

盛子豪，范 庚，漢 田

（海軍航空大學，山東 青島 266041）

對變后掠翼飛行器的研究始于20 世紀40 年代，德國研發了世界第1 種變后掠翼戰斗機——Me P.1101，50年代，美國貝爾公司在此基礎上設計出貝爾X-5。60 ～70 年代，變后掠翼飛行器進入了發展的黃金期，最具代表性的如F-14、米格-23、蘇-24 等。之后，由于技術受限，變后掠翼逐漸被固定翼取代。近年來，隨著計算機輔助、材料和芯片等技術的發展，使得變后掠翼飛行器迎來了新的發展機遇，美國、俄羅斯等國已爭相開展對可變后掠翼的研究[1-4]。

國內學界在變形翼方面的研究，如：朱華、劉衛東等通過比較智能材料作動器的性能，提出利用超聲電機驅動飛行器變形[5]；吳俊、陸宇平提出1 種分布式協同控制方案來控制機翼變形[6]。以上研究都具有一定的代表性。

變后掠翼作為變形翼的1 種，受到更多地關注。1980年，我國以強-6作為第一代變后掠翼飛行器。近年來，董彥非等人利用CFD 技術，對多條件下變后掠翼飛行器的機翼后掠角控制進行了探究，通過插值法補充數據并采用遺傳算法進行全局尋優[7-9]。在后掠翼可變的結構設計上，王釗提出1 種自適應變后掠翼機構，能根據最佳變后掠角規律，實現被動控制飛機的變后掠過程[10]。

變后掠翼飛行器在民航領域應用較少，更多的是應用于軍事。遠距離突防性能是未來武器發展趨勢，續航則是關鍵性能。美國最新的增程式導彈是在原有域外攻擊巡航導彈的基礎上，對射程、精準度、戰斗部穿透力和任務規劃等方面進行了升級，它在結構上的最大特點就是采用了水平翼布局，這種改變大大提升了武器性能。該型導彈的寬翼展對飛機的結構及掛載能力提出了更高要求。更為先進的聯合空面防區外導彈（JASSM）則對此進行了改進，雖同樣采用了水平翼布局，但不同之處在于它采用了伸縮翼，這樣可以減小彈倉的占用空間，不僅適配更多機型，而且同時又可達到遠距離攻擊的目的。但該型導彈的彈翼只具備伸縮特性，并不能根據當前導彈工況來改變后掠角度[11]。我國學者也在導彈領域進行了相關探索：王江華、谷良賢等以遺傳算法與模式搜索法相結合的混合優化策略改進了1種伸縮彈翼模型的控制策略[12]；李偉明等采用粒子群算法形成1 種基于迎角與后掠角控制的彈道優化設計方法[13]；夏美從生存性、可用性、殺傷力及對抗環境下表現等方面論證了亞音速反艦導彈更具優勢[14]。同時，從美軍導彈的武器特性中可以了解到，該類型武器均是亞音速巡航。所以，本文飛行器考慮到長續航因素，將速度范圍定為亞聲速以下。

國內研究多采用遺傳算法和插值法對變后掠翼在全速度下進行全局尋優。本文在1種新型變后掠翼飛行器模型基礎上，尋求變后掠翼飛行器在單速度下更為簡單的全局尋優方法。嘗試使用多項式數學模型替代原有模型進行，并通過CFD仿真軟件對其進行仿真與驗證。總體研究思路如下：

1）設計新型變后掠翼飛行器模型，通過Solid-Works軟件建模；

2）選定飛行器迎角、速度和后掠翼的后掠角度范圍及變化步長；

3）設置模擬流體力學仿真邊界、網格、來流狀態等參數；

4）對不同狀態下的飛行器模型進行CFD模擬；

5）選取在不同狀態下最佳后掠翼后掠角度；

6）對所有結果進行后處理，并建立該飛行器在單一速度下的后掠翼最優后掠角預測模型；

7）將預測模型結果與CFD 計算結果進行對比，驗證模型準確性。

1 變后掠翼飛行器建模

對飛行器進行了彈翼布局選型，彈翼、尾翼設計，機體（包含頭部、機身、尾部）設計。參數如圖1所示。

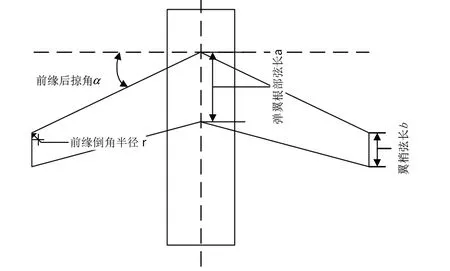
圖1 飛行器尺寸參數Fig.1 Size parameters of the aircraft

整體上，飛行器的尺寸設置參考了部分通用機體尺寸，在細節上做了如下規劃：

1）選用激波影響相對較小，內部空間相對較大的拋物線形頭部作為外形；

2）選用阻力小、拋物線形作為尾部；

3）尾翼結構采用了對稱翼型剖面NACA0009，根梢比1.25；

4）彈翼根梢比η=a b=1.5 ，前緣倒角半徑r=150 mm；

5）機翼翼型剖面采用NACA6409（屬典型非對稱翼型剖面）；

6）飛行器兩翼前緣后掠角度α，其可變范圍是[15°，45°] ，為方便描述，本文所稱后掠角均指前緣后掠角。

建模后飛行器，如圖2所示。

圖2 變后掠翼飛行器模型Fig.2 Model of variable-sweep wing aircraft

當彈翼完全展開時，飛機處于大展弦比的狀態，理論上該狀態適用于低速飛行，有利于提供良好的升阻比；當彈翼折疊，展弦比變小，根梢比變大，理論上該狀態適用于高速飛行[15]。同時，為了不影響機身的氣動布局，在該飛行器機身中下部預留一部分艙內空間，以安放彈翼。

為了得到定量評判，本文以升力、阻力、升阻比及俯仰力矩作為評價氣動性能的指標。在不同速度，迎角、彈翼后掠角度下，對飛行器氣動性能進行全覆蓋式的仿真，根據仿真結果來探究后掠角度規律并進行預測及驗證。

2 仿真理論基礎及條件范圍設定

本文采用COSMOS作為CFD仿真計算軟件。其理論基礎為Navier-Stokes方程[16]：

仿真也考慮了湍流的模擬，湍流模型為強度-長度模型以及湍流耗散模型。本文為減小湍流影響，選用了默認的強度-長度模型，湍流強度為0.1%，湍流長度為0.003 5 m[17]。

網格劃分可以使用結構網格、非結構網格及混合型非結構網格[18]。這里選用結構網格，在模型曲面處進行多級網格細分。仿真前，其他預設環境條件，見表1。

表1 其他預設環境條件Tab.1 Other preset environmental conditions

因為全覆蓋式仿真計算量大，所以在最終仿真前要對仿真范圍、方式進行進一步規定，根據模型結構、飛行條件選定范圍，如表2所示。

表2 計算仿真范圍Tab.2 Simulation range

須說明：

1）為了避免數據過多，彈翼后掠角度變化步長設置為2.5°，飛行器速度變化步長馬赫數為0.2；

2）經篩選，共選取39個關鍵點進行CFD仿真，每個關鍵點都要在0°～14°迎角條件（步長2°，共8 次）下進行仿真，共進行312次仿真。

3 仿真結果

仿真結果表明，升阻比的大小受速度、迎角、后掠角度影響，其中迎角對升阻比影響較大。同樣，不同后掠角度、速度下的最大升阻比對應的迎角也是不同的。現將仿真結果進行后處理，如果速度和后掠角不變，將迎角從0°～14°（步長為2°）變化過程中所得到的升阻比作為1組數據的話，可得39組數據。如當飛行馬赫數為0.4，后掠角為15°時，將由迎角變化所得的8個升阻比數據作為1組，如表3所示。

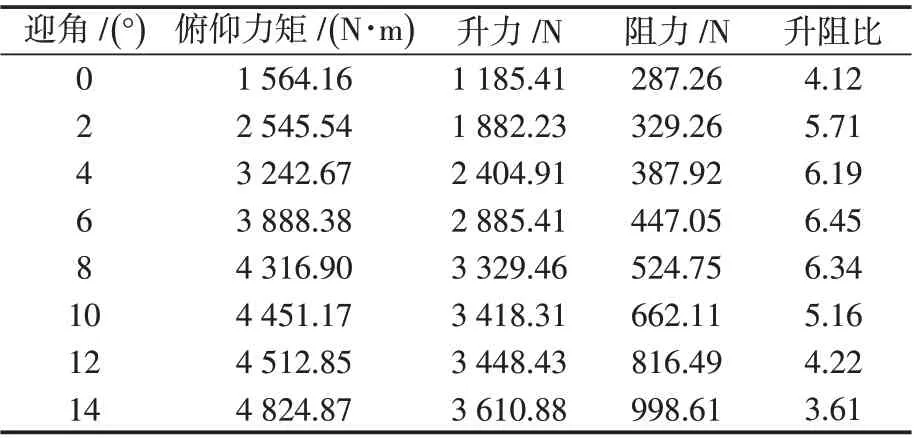
表3 飛行馬赫數為0.4、后掠角15°，隨迎角變化所得仿真結果Tab.3 Simulation results with the angle of attack when the Mach mumber is 0.4 and the swept-back angle is 15°

由于本文旨在預測最大升阻比的變化趨勢，所以只取每組數據中數值最大的升阻比及其當時對應的速度及后掠角度進行研究。可得出在不同速度、后掠角下每組數據和數值最大的升阻比對應的升力、阻力、俯仰力矩和升阻比變化趨勢，如圖3（此圖未標注每個數據對應的迎角）所示。

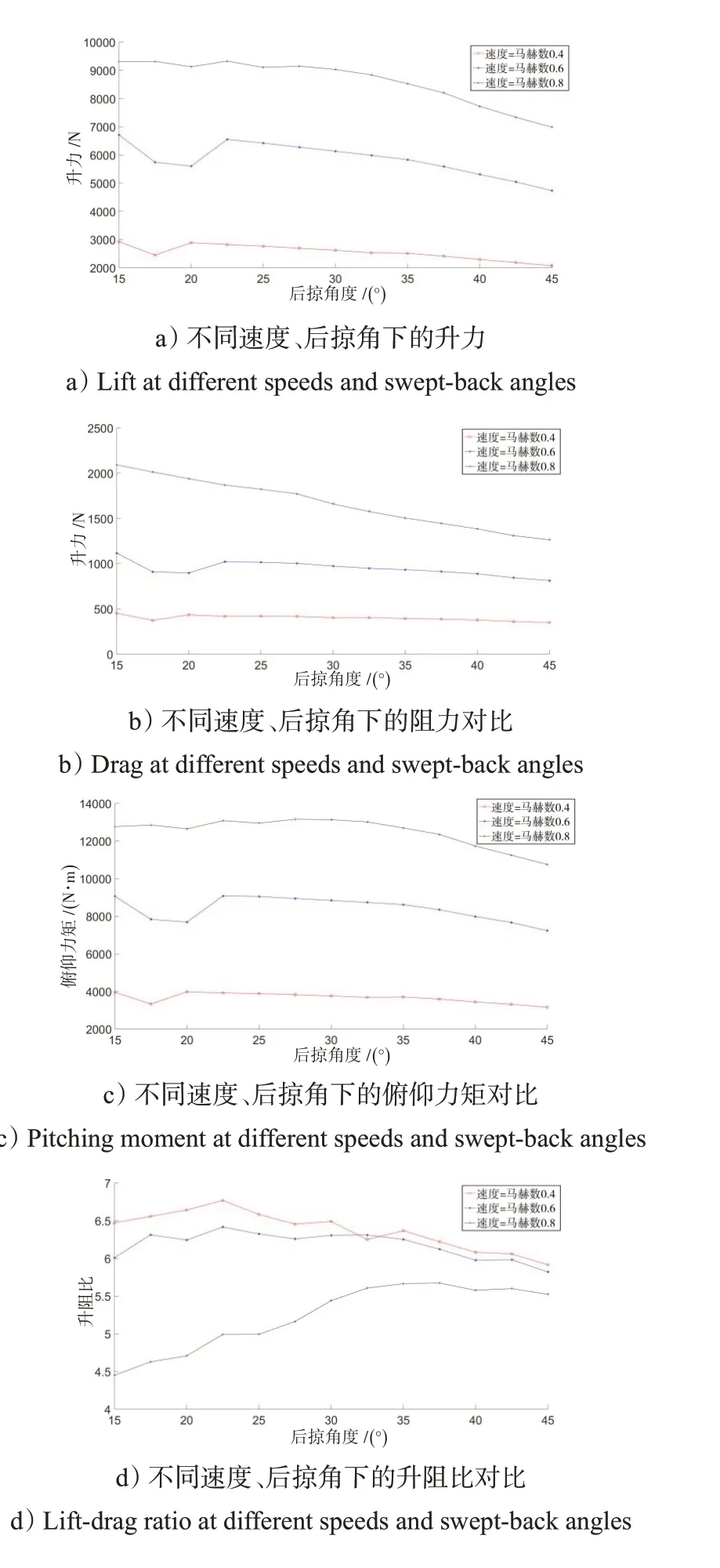
圖3 不同速度、后掠角度下各項仿真結果Fig.3 Simulation results at different speeds and sweep-back angles

仿真結果得出：該飛行器在飛行馬赫數為0.4 時最大升阻比約為6.76，迎角約為6°，此時彈翼前緣后掠角度為22.5°；飛行器在飛行馬赫數為0.6 時最大升阻比約為6.41，迎角約為6°，此時彈翼前緣后掠角度為22.5°；飛行器在以馬赫數為0.8 時最大升阻比約為5.703，迎角約為4°，此時彈翼前緣后掠角度為37.5°。

通過上述分析可知，在以上的取值范圍內，會有1個升阻比的極大值，但它是否是唯一的極大值，這需要知道各組數據中最大的升阻比的變化規律，而變化規律僅通過這39 組數據的離散結果是無法得到的。可以利用CFD軟件進行大量仿真實驗，再通過曲線擬合得到的結果，找出其中的規律，最終確定變化策略。由于這一過程需要耗費大量的計算資源及時間，所以，本文提出另1種方法，根據已有數據建立數學模型，預測最優的后掠角度。

4 預測模型及驗證

為了驗證該方法的可行性并減少計算量，根據已有的仿真結果，將升阻比及對應的迎角數據進行整合，得到曲線，如圖4所示。

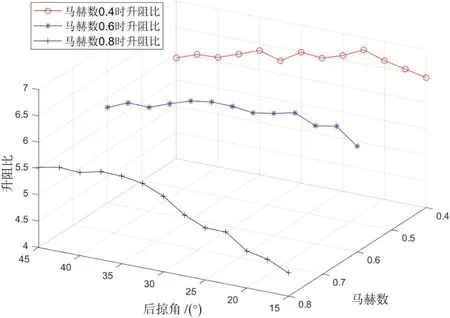
圖4 變后掠翼飛行器升阻比Fig.4 Lift-drag ratio of variable-sweep wing aircraft

根據條件范圍可知，仿真過程中，將彈翼后掠角度的步長設置為2.5°，所得到的值是非連續性的。預測模型建立的思路是根據對上述各組數據取某一速度下的結果進行擬合，通過連續曲線就能找到在該速度下的最值點，即最大升阻比。

多項式曲線、插值曲線、局部加權回歸曲線為數學模型的建立提供了參考依據。通過對比不同曲線，判斷擬合后曲線與仿真曲線的誤差及方差，最終，確定采用多項式曲線對數據進行擬合較為合適。經過次數為1～9 的擬合后，發現從4 次多項式擬合曲線趨勢可以接近仿真曲線，雖然5 次及以上多項式的擬合值與仿真值在均方差和確定系上表現數更優，但是明顯出現了“過擬合”的現象。在馬赫數為0.4 時，擬合曲線與仿真數據，如圖5所示。

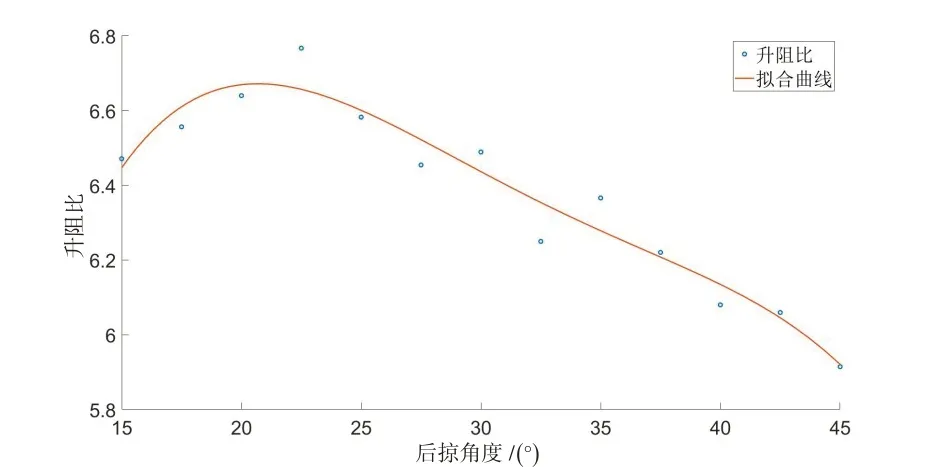
圖5 4次多項式曲線擬合Fig.5 Fitting curve of quartic polynomial

同理，在飛行馬赫數為0.6和0.8時，4次多項式依然能夠較好地擬合升阻比在后掠角度變化時的趨勢，因而，飛行器升阻比在不同前緣后掠角的擬合曲線確定為4次多項式。

根據所得曲線，可以確定該飛行器在飛行馬赫數為0.4 時，曲線極值點為后掠角約為21°時獲得，為6.67。在此后掠角下，當迎角為6°時，最大的升阻比為6.832。可以預測出該模型在不同速度、彈翼后掠角度下的飛行器后掠翼的最優后掠角度。

根據同樣的方法，將飛行馬赫數為0.6和0.8時的擬合值與仿真驗證結果進行對比，如表4所示。

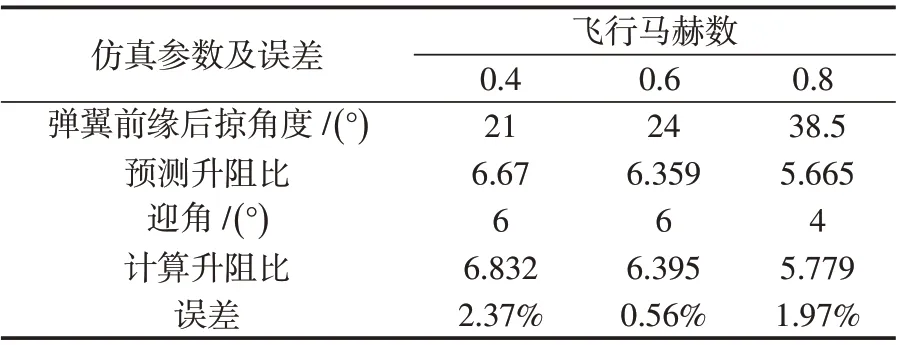
表4 仿真結果對比Tab.4 Comparison of simulation results and calculated values

從上述結果可知，將4 次多項式的擬合及仿真計算結果進行對比，可得在3 種速度下的誤差均小于3%，說明4次多項式模型基本可以滿足對后掠翼飛行器在不同速度下最優后掠角度的預測。

5 結論

本文基于1 種新設計的飛行器，探究了變后掠翼單速度最優后掠角變化規律，并通過仿真得到基于4次多項式的數學模型，可大致擬合該規律。經過驗證預測模型所得最優后掠角與仿真計算值誤差在3%以下。這種單速度模型相比于利用遺傳算法等方式進行全局尋優更為簡單，為單速度場景下變后掠翼后掠角控制率提供了理論上的數學模型參考。由于受實驗場所和器材等因素限制，本文模型準確性仍須通過風洞試驗實測才能得到最終驗證。后續，將結合更復雜的曲面建模、深度學習等知識領域對變后掠翼控制規律做進一步研究。