基于線性約束最小方差原則的穩健快速自適應脈沖壓縮方法
裴家正, 黃 勇,*, 陳寶欣, 關 鍵, 陳小龍
(1. 海軍航空大學航空作戰勤務學院, 山東 煙臺 264000; 2. 中國人民解放軍92337部隊, 遼寧 大連 116000)
0 引 言
基于大時寬-帶寬積信號的脈沖壓縮技術可以同時保證雷達系統對較遠雷達探測距離和較高距離分辨率的要求。作為脈沖壓縮技術的常用方法,匹配濾波(matched filter, MF)是在點目標和高斯白噪聲條件下,以最大化輸出信噪比為準則的最優線性濾波器[1-3]。
然而實際應用中,MF的輸出存在強目標距離旁瓣遮蔽其他弱目標等問題。為了更好地抑制旁瓣,多種失配濾波方法[4-8]在一定程度上實現了抑制效果。此外,較有代表性的便是基于迭代最小均方誤差(iterative minimum mean square error, RMMSE)準則的自適應脈沖壓縮(adaptive pulse compression, APC)方法[9],該方法迭代地利用鄰近距離單元的功率值為每個距離單元設置自適應濾波器,構造自適應零陷壓低旁瓣。隨后Blunt不僅將APC方法推廣至共享頻帶的多基地雷達中[10],又研究了自適應脈沖壓縮修復(pulse compression repair, PCR)方法[11]將MF的輸出結果作為發射波形進行APC,對多普勒失配和系統誤差具有更強的穩健性;還提出了先進行多普勒補償,再進行APC抑制運動目標的距離旁瓣[12-13]。為進一步降低APC方法較高的計算量,Blunt等結合降維算法提出了快速APC (fast APC, FAPC)方法,主要包括抽取分塊FAPC(decimation FAPC, DFAPC)方法和連續分塊FAPC(contiguous block FAPC, CFAPC)方法[14-15]。FAPC方法在減少計算量的同時保持了APC的大部分性能增益,但降低了算法的自由度,會在較密集的散射環境中抑制小目標。因此Higgins等后續提出了基于最小方差無畸變響應(minimum variance distortionless response, MVDR)原則的CFAPC(MVDR-CFAPC)方法[16],將增益保留在小目標上,從而提高了檢測性能。
在APC方法基礎上,近年來的研究不僅有借鑒空域陣列的處理方法提高了APC方法抑制干擾、雜波的能力[17];也有借鑒線性貝葉斯理論、并行運算等降低APC方法的計算量[18-19];還有探索多輸入輸出雷達體制下的APC方法[20-21],這些改進不但解決了相應的問題,還依然具備較好的旁瓣抑制效果。但以上研究大部分在討論APC方法性能時都默認距離單元內回波采樣點位于目標點上。對于常見的連續時間相位調制波形,如線性調頻(linear frequency modulation, LFM)信號波形等,由于目標點隨機分布于距離單元內,因此在回波采樣的過程中極有可能回波采樣點沒有位于目標點上,造成二者失配的情況(也可稱為采樣失配)。在APC處理中,如果出現采樣失配,基于回波數據的APC濾波器將難以形成深凹口,其性能損失十分明顯。為此,Henke等將基于最小二乘的失配濾波方法和APC方法應用于調頻波形,提出對回波過采樣抑制采樣失配所引起的距離旁瓣[22],但是對回波過采樣所帶來的計算量十分顯著。李秀友等通過設置主瓣寬度和干擾零點約束條件,提出了一種基于線性約束最小方差(linearly constrained minimum variance, LCMV)準則的APC方法[23],以解決采樣失配和強目標距離旁瓣遮蔽弱目標的問題,然而該方法需要估計強弱目標的相對強度和位置,實際中難以劃分合適的強弱目標相對值。
本文在MVDR-CFAPC方法的基礎之上進行改進。MVDR-CFAPC方法在LFM信號波形采樣失配時具備一定的穩健性,但是其穩健性并不穩定。為此,本文借鑒導向矢量失配情況下基于線性約束最小方差原則的穩健自適應波束形成算法,在不對回波過采樣的前提下提出將基于LCMV原則的CFAPC方法應用于LFM信號的脈沖壓縮處理中,在LFM信號回波采樣匹配和失配情況下都具備較為穩定的距離旁瓣抑制性能。本文最終通過仿真和實測數據實驗驗證了該方法的穩健性。
1 采樣失配問題的相關分析
假設場景中共有L個距離單元,在每個距離單元中有Nsample個采樣點,每個距離單元取一個采樣點。采樣的發射信號波形可以通過準確抽取每個距離單元內的第1個采樣點取得,發射信號波形的N維采樣點組成的矢量可以表示為s=[s(0),s(1),…,s(N-1)]T。采樣的回波信號波形也是在每個距離單元中Nsample個采樣點里抽取其中的一個,如果回波信號波形的采樣點位于目標點上,則視為采樣匹配。采樣匹配時距離單元l(l=0,1,…,L-1)處的雷達回波信號y(l)為
y(l)=xT(l)s+v(l)
(1)
式中:x(l)=[x(l),x(l-1),…,x(l-N+1)]T表示場景真實距離維響應的N點連續采樣;v(l)為距離單元l處的加性高斯白噪聲。MF的脈壓輸出表示為
xMF(l)=sHy(l)=sHAT(l)s+sHv(l)
(2)
式中:y(l)=[y(l),y(l+1), …,y(l+N-1)]T為回波的N點連續采樣且y(l)=AT(l)s+v(l);A(l)=[x(l),x(l+1),…,x(l+N-1)];v(l)=[v(l),v(l+1),…,v(l+N-1)]T為噪聲矢量;(·)H為共軛轉置運算。
MVDR-APC方法通過構造代價函數J(l)=E[|x(l)-wH(l)y(l)|2]推導最優濾波器系數,E(·)表示期望[9,24]。在單位增益無畸變約束wH(l)s=1下,利用拉格朗日乘數法最小化代價函數[25]可得
(3)
式中:Ry(l)=Rx(l)+R(l)為回波協方差矩陣,R(l)=E[v(l)vH(l)]為噪聲協方差矩陣,Rx(l)為信號協方差矩陣:
(4)
其中,ρ(l+n)=|x(l+n)|2為距離單元(l+n)處的功率值;sn為以s為基礎進行移位的N維矢量:
(5)
由于無法準確確定目標點在距離單元內的分布,如果采樣的LFM信號回波波形在Nsample個采樣點中抽取的采樣點不是目標點,那么二者之間就是失配的。令回波采樣點與目標點之間的失配時間為Δt(-0.5Ts<Δt≤0.5Ts,Ts為回波采樣間隔),如圖1(a)所示,回波采樣點超前目標點時Δt為負;如圖1(b)所示,回波采樣點落后目標點時Δt為正。

圖1 采樣失配時間Δt示意圖
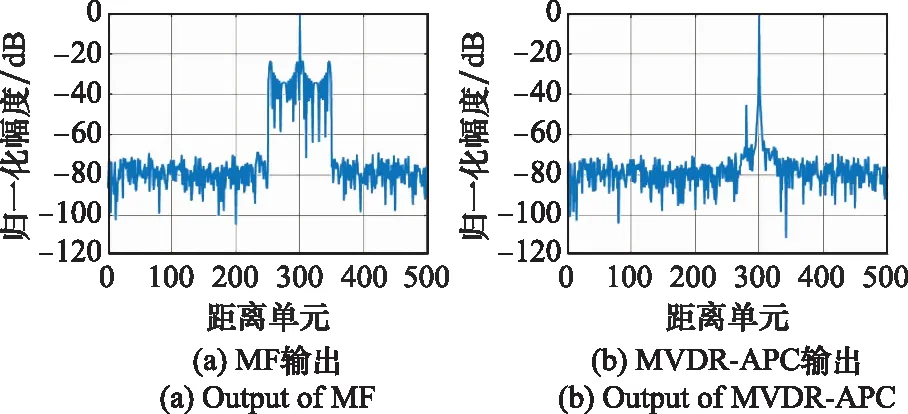
以平靜海面上一艘海盜游艇隱藏在貨輪周圍企圖掩蓋行蹤的情況為例,仿真場景中設置一強一弱兩目標A和B,信噪比分別為60 dB和15 dB。圖2為仿真回波采樣點和強目標點之間采樣匹配和失配0.5Ts情況下(不存在脈內多普勒頻率)的脈壓輸出。在采樣匹配情況下MF(包括加Taylor窗的MF)脈壓輸出帶有明顯的距離旁瓣,而MVDR-APC方法抑制了距離旁瓣。但在采樣失配0.5Ts情況下,MVDR-APC方法的脈壓輸出中強目標也產生了較大的距離旁瓣,遮蔽了弱目標,與采樣匹配的情況相比,性能明顯下降。

圖2 采樣匹配和采樣失配0.5 Ts時MF,加Taylor窗MF, MVDR-APC的輸出
2 LCMV-CFAPC
為了在LFM信號的APC處理中抑制因采樣失配而引起的距離旁瓣,本節首先證實MVDR-CFAPC方法對LFM信號波形采樣失配具備一定的穩健性;而后改進MVDR-CFAPC方法,得到更穩健的LCMV-CFAPC方法。
2.1 針對LFM信號脈壓的MVDR-CFAPC方法
CFAPC方法將APC處理的N維信號模型連續分割成M塊,并且每一塊中的元素個數為K=N/M,得到的第m塊(1≤m≤M)信號模型[14]為
(6)
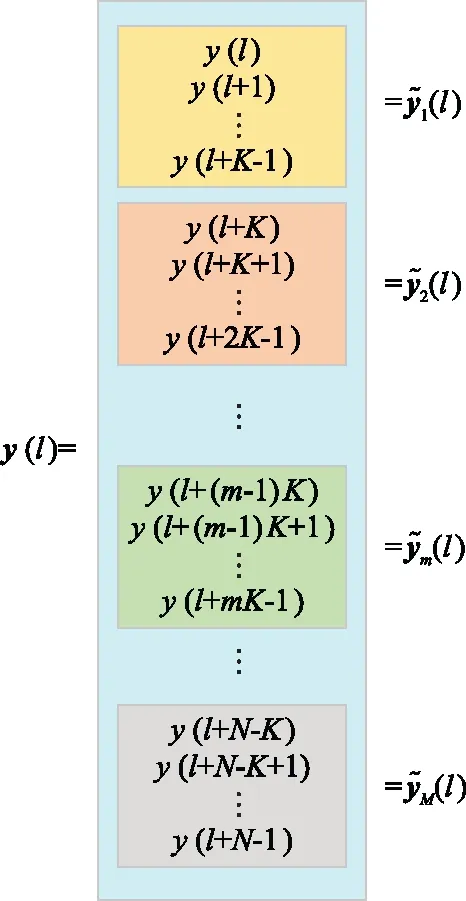
圖3 回波信號的連續分塊示意圖
MVDR-CFAPC方法的代價函數通過拉格朗日乘數法表示為
(7)
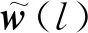
(8)
其中,
(9)
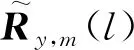
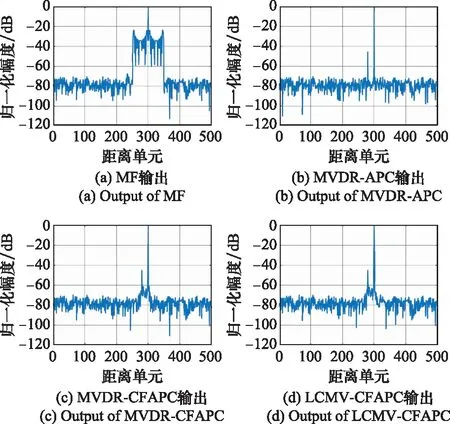
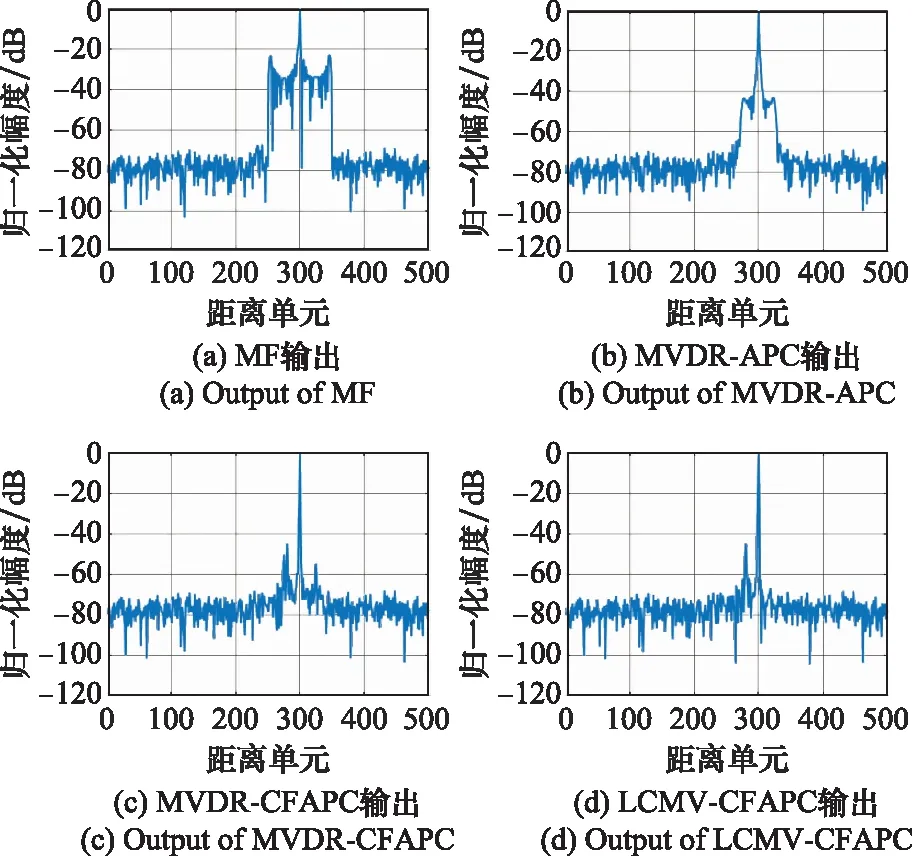
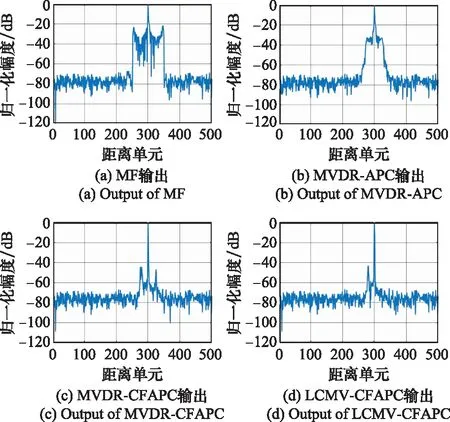
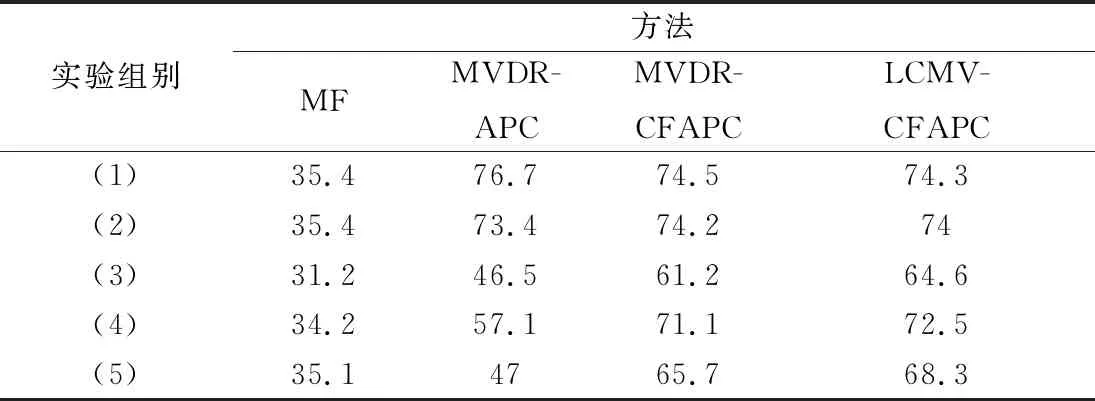
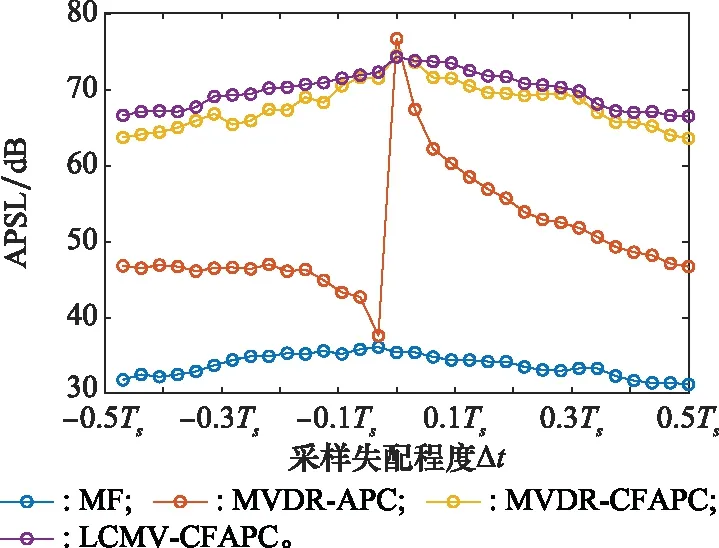
相比相位編碼信號,LFM信號多普勒容忍性更強,但是對采樣失配問題更敏感。在LFM信號回波采樣失配時,MVDR-CFAPC方法相比MVDR-APC方法處理時間較短(因為K 圖4為MVDR-CFAPC方法在圖2場景中強目標點采樣失配0.5Ts時M取不同值的脈壓輸出結果。當分塊數M取接近于波形長度N的最大約數,即M=N/2時,在采樣失配時間維放置的零點最多,相比M取其他值脈壓主瓣寬度以及旁瓣抑制更優。 圖4 采樣失配0.5 Ts時MVDR-CFAPC方法中 M取不同值的輸出 但當采樣失配時間為其他值(為節省篇幅圖5以采樣失配0.2Ts和-0.25Ts情況為例),在強目標點左右各N/2處旁瓣有所抬升,可見MVDR-CFAPC方法在(-0.5Ts, 0.5Ts]的采樣失配區間內的性能并不穩定,因而需要繼續改進得到更穩健的輸出。 圖5 采樣失配0.2 Ts和-0.25 Ts情況下的MVDR-CFAPC輸出 為了保證APC方法在采樣失配區間內都能保持更好的穩健性,本節借鑒導向矢量失配情況下的穩健自適應波束形成算法[26-31],在MVDR-CFAPC方法中的無畸變約束條件基礎上施加更多的約束條件[32],得到LCMV-CFAPC方法,通過增加的約束抑制不希望存在的距離旁瓣以獲得更穩定的脈壓輸出。 (1) 設置零點約束條件 (10) 由此,LCMV-CFAPC方法的全維代價函數為 (11) (3) 利用拉格朗日乘數法,全維代價函數重新寫為連續分塊之和的形式: (12) (13) 式中:Cm是由約束條件矩陣C的第(m-1)K+1行到第mK行組成的第m個子陣,且 (14) (15) 式中:sm,k是以sm(s的第(m-1)K+1個到第mK個元素組成的第m個分塊矢量)為基礎進行移位的K維矢量: sm,k=[s((m-1)K-k),s((m-1)K-k+1),…,s(mK-k-1)]T (16) 若在移位過程中,k<-N+mK或k>(m-1)K使得(m-1)·K-k,(m-1)K-k+1,…,mK-k-1中的一個或多個索引值為小于0或大于N-1時,需要將sm,k中對應位置的元素用0補齊。 (4) 設置分塊協方差的置零條件 ρ(l+k+(m-1)K)=0, 0<|k+(m-1)K| (17) (18) (6) 迭代運算 當連續分塊數M取N/2時,LCMV-CFAPC方法的脈壓主瓣寬度仍然為最優。按照(1)~(5)計算每個距離單元的最優權矢量,迭代5~6次便可通過LCMV-CFAPC方法實現較穩健的脈壓輸出。 為了較全面地分析LCMV-CFAPC方法的性能,本節首先考慮各個方法分別在圖2場景中采樣匹配、脈內多普勒失配、采樣失配0.5Ts、采樣失配0.2Ts、采樣失配-0.25Ts等仿真情況下的脈壓性能。所有仿真場景下將強目標左右N-1個距離單元范圍內計算平均峰值旁瓣電平(average peak sidelobe level, APSL)作為性能指標,作為估計值,需要多次仿真取平均,一次仿真的APSL計算為 (19) 式中:lmax為強目標所在距離單元;SNR(lmax)為強目標的信噪比;I為lmax左右N-1個距離單元集合,且不包含其他目標主瓣位置;SNR(i)為距離單元i處的信噪比。之后本節在多目標采樣失配程度互異的仿真條件下比較各個方法的距離旁瓣抑制效果。最后借助實測數據實驗,進一步對比分析方法性能。 仿真場景中一共有L=500個距離單元。LFM信號帶寬B為5 MHz,時寬τ為10-5s,時寬-帶寬積Bτ=50,N=50。令采樣頻率Fs等于帶寬B即可使一個距離單元中有一個回波采樣點,且采樣間隔Ts=1/B。為了仿真模擬信號的數字采樣過程,Fs為160 MHz,則Nsample=32,一個距離單元中有32個回波采樣點。為了簡化問題的表述,假設目標點位于距離單元中的第17個采樣點。如果回波采樣點是通過抽取每個距離單元中的第17個采樣點取得,則為采樣匹配情況;如果回波采樣點不是第17個采樣點,則為采樣失配情況。 (1) 采樣匹配情況下的性能仿真 按照圖2的仿真場景,兩目標A和B信噪比分別為15 dB和60 dB,位于第280個和第300個距離單元。在采樣匹配情況下,目標無脈內多普勒頻率時,各方法的脈壓性能如圖6所示。 圖6 采樣匹配時各方法的脈壓性能 圖6中MF輸出存在強目標旁瓣遮蔽弱目標的現象,APSL為35.4 dB。全維度的MVDR-APC方法在采樣匹配情況下的脈壓效果最好。MVDR-APC,MVDR-CFAPC和LCMV-CFAPC方法在采樣匹配時的脈壓輸出APSL分別為76.7 dB,74.5 dB,74.3 dB, 3種方法都可以抑制強目標旁瓣,還原出弱目標的主瓣。 (2) 脈內多普勒失配下的性能仿真 本組實驗令目標A脈內多普勒800 Hz,目標B脈內多普勒1 000 Hz,對回波采樣點與目標點采樣匹配的情況繼續進行分析。 在具有脈內多普勒頻率時MVDR-APC方法的脈壓輸出強目標距離旁瓣存在但不明顯,APSL為73.4 dB,相比于無脈內多普勒頻移時下降3.3 dB。由于CFAPC方法對脈內多普勒頻率的容忍性更強,MVDR-CFAPC和LCMV-CFAPC方法的脈壓輸出結果較好,APSL分別為74.2 dB和74 dB。 (3) 采樣失配0.5Ts下的性能仿真 目標A和B的脈內多普勒頻率與(2)相同,回波信號波形采樣失配0.5Ts情況下各個方法的脈壓性能如圖8所示。 圖7 脈內多普勒失配時各方法的脈壓性能 圖8 采樣失配0.5 Ts時各方法的脈壓性能 根據圖8與圖7的對比可得出,脈內多普勒失配與采樣失配同時存在時,采樣失配對APC方法的影響占據主導地位。此時MVDR-APC方法的脈壓旁瓣已經完全遮蔽了附近的弱目標。MVDR-CFAPC和LCMV-CFAPC方法仍然可以在脈內多普勒頻率與采樣失配同時存在時達到較好的旁瓣抑制性能,但是二者的輸出之間仍然存在較細微的差別。 (4) 采樣失配0.2Ts下的性能仿真 目標A和B的脈內多普勒頻率與(2)相同,回波信號波形采樣失配0.2Ts情況下各個方法的脈壓性能如圖9所示。圖9中最明顯的是MVDR-CFAPC方法的脈壓輸出在強目標左右N/2處出現了新的距離旁瓣,其APSL為71.1 dB。而LCMV-CFAPC方法因為添加了抑制旁瓣干擾的約束,仍然可以達到較好的旁瓣抑制性能,其APSL為72.5 dB。 圖9 采樣失配0.2 Ts時各方法的脈壓性能 (5) 采樣失配-0.25Ts下的性能仿真 本組實驗采樣失配時間-0.25Ts,且目標A、B的脈內多普勒頻率與(2)相同。圖10中MVDR-CFAPC方法強目標左右N/2處距離旁瓣也存在。雖然APSL為65.7 dB,稍好于采樣失配0.5Ts的情況,但LCMV-CFAPC方法能夠在失配時間為-0.25Ts時保持更好的旁瓣抑制性能,APSL保持在68.3 dB。 圖10 采樣失配-0.25 Ts時各方法的脈壓性能 為更直觀地比較,以上不同實驗組各個方法的APSL如表1中所示。綜合比較而言,LCMV-CFAPC方法更具備穩健性。 表1 各個方法在仿真實驗中脈壓輸出的APSL 考慮不同采樣失配時間下不同方法的性能,根據以上仿真場景得出無脈內多普勒時以上4種方法的APSL僅隨采樣失配時間Δt變化的關系。從圖11可以明顯看出,MVDR-APC方法在采樣匹配的情況下脈壓效果極佳,可是一旦發生采樣失配問題,其脈壓的APSL急劇下降。由于MVDR-CFAPC方法與LCMV-CFAPC方法是降維版本,采樣匹配情況下的APSL都稍低一些;但是在采樣失配情況下APSL數值更大且相比MVDR-APC方法的變化更平緩,說明兩種方法都更穩健。Δt在采樣失配區間變化時,LCMV-CFAPC方法的APSL比MVDR-CFAPC方法的更大一些。另外,圖9和圖10中MVDR-CFAPC方法脈壓輸出旁瓣有所抬升,綜合之下LCMV-CFAPC方法仍然更加穩定。 圖11 APSL與采樣失配時間Δt的關系圖 本節實驗在場景中隨機設置12個目標,目標的信噪比和脈內多普勒頻率分別在[15 dB, 60 dB]和[-1 000 Hz, 1 000 Hz]的區間內隨機取值。在多目標每個目標點的采樣失配時間在(-0.5Ts, 0.5Ts]區間之間隨機取值的情況下各個方法的脈壓輸出性能對比如圖12所示。圖中經過脈壓后可被明顯發現的目標被紅色圓形標出。 圖12 采樣失配與脈內多普勒同時發生時多目標不同方法的脈壓性能 在目標較多時MVDR-APC方法的脈壓性能退化依然嚴重,MVDR-CFAPC方法的脈壓輸出也存在強目標脈壓旁瓣遮蔽部分弱目標的現象。為通過數值比較各種方法在多目標采樣失配場景下的性能,本節計算每個目標的APSL取平均值作為量化比較的性能指標。在MF的輸出中4個弱目標被強目標旁瓣遮蔽,目標APSL平均值為18.97 dB,進一步說明了MF的脈壓具有較高旁瓣的問題。MVDR-APC方法的輸出中4個弱目標同樣被強目標旁瓣遮蔽,目標APSL平均值為25.99 dB。MVDR-CFAPC方法雖相比MVDR-APC方法較好,但其輸出中仍然有兩個弱目標被強目標旁瓣遮蔽,目標APSL平均值為35.47 dB。綜合比較而言LCMV-CFAPC方法性能最優,其輸出中各目標的主瓣都比較明顯,目標APSL平均值為40.04 dB。可以看出,在整個仿真實驗中,MVDR-CFAPC和LCMV-CFAPC方法對于脈內多普勒頻率和采樣失配同時存在時相較于MVDR-APC方法都更加穩健,但總的來說LCMV-CFAPC方法的穩健性更好。 本節實驗選取部分采自X波段雷達實測數據,分別利用MF,MVDR-APC,LCMV-CFAPC 3種方法對該實測數據進行脈沖壓縮處理。此X波段雷達所發射信號波形的時寬帶寬積為75,且實測數據中共存在4個目標,大致位于場景中的第480,第550,第590和第1 050個距離單元處。3種方法的脈壓輸出如圖13所示,圖中的綠色圓形標記出了經過MF方法和MVDR-APC方法脈壓輸出無法發現的目標。由圖13可知,MF方法的脈壓輸出中強目標的脈壓旁瓣直接遮蔽了綠色圓形標記的弱目標;MVDR-APC方法稍好一些,強目標的脈壓旁瓣被有效地抑制,但仍然遮蔽了綠色圓形標記的弱目標;LCMV-CFAPC方法的脈壓輸出中可以較輕易地發現該弱目標,進一步證實LCMV-CFAPC方法的脈壓輸出更清晰,處理實測數據時該方法的脈壓處理性能仍然更加優異。 圖13 處理雷達實測數據時不同方法的脈壓性能 由于APC方法設計迭代運算,分析時只分析一次迭代運算中的計算成本。在時域中實現的MF相當于僅有一次迭代,而且其計算成本為每個距離單元進行N次乘積,對每個距離單元其計算成本為N[15]。常規的MVDR-APC方法可根據矩陣求逆定理進行秩一更新[9],快速計算每個單獨的距離單元的N×N維協方差矩陣。針對每個距離單元,其計算成本為6N2+14N[15]。 MVDR-CFAPC方法對協方差矩陣分塊,對應于第l個距離單元的信號協方差矩陣與第l-K個距離單元的協方差矩陣的子陣之間具有如圖14所示的對應關系,因此前K個距離單元之后每個距離單元的協方差矩陣只需更新一個K×K維矩陣[15]。另外MVDR-CFAPC方法也可以進行快速矩陣更新,其計算成本為N2(3/M+3/M2)+N(1+13/M)[15]。 圖14 CFAPC中與子陣的對應示意圖 LCMV-CFAPC方法一方面增加了零點約束條件,另一方面是分塊協方差的置零操作。二者的計算成本一共為N2/M+N2/M2+2N,使得LCMV-CFAPC方法的計算成本為N2(4/M+4/M2)+N(3+13/M)。算法中M=N/2,可見針對單個距離單元,LCMV-CFAPC方法一次迭代的計算成本明顯低于MVDR-APC方法,仍屬于快速APC方法。 為了進一步分析算法復雜度,表2~表4列舉出第4.1~第4.3節中各個方法在MatlabR2019b和COREi7-9750H環境下多次運行得到的一次迭代平均耗時比較。 表2 第4.1節中各方法一次迭代的平均耗時 表3 第4.2節中各方法一次迭代的平均耗時 表4 第4.3節中各方法一次迭代的平均耗時 從表2和表3仿真實驗耗時對比中看出,相比于MF,APC方法耗時確實較長。雖然MVDR-CFAPC和LCMV-CFAPC方法的平均耗時長于MVDR-APC方法,但是其迭代次數是MVDR-APC方法的兩倍。如果按照一次迭代耗時來比較,LCMV-CFAPC方法耗時介于MVDR-CFAPC和MVDR-APC方法之間。 根據表4實測數據實驗耗時對比仍然可以得到相同的結論,對于第4.3節實測數據處理,由于實驗測試是通過有限的軟硬件來實現的,表4中的結果可作為參考。耗時結果跟環境配置緊密相關,具體到實際運用中的耗時還是要結合具體算法,實驗過程以及數字信號處理計算平臺繼續優化。 LFM信號在現代雷達信號處理中應用廣泛。信號回波波形采樣點與目標點之間采樣失配對APC影響十分明顯。本文在LFM信號脈沖壓縮處理的應用場景下,借鑒導向矢量失配情況下的穩健自適應波束形成算法,以CFAPC為基礎先增加了零點約束條件,又對分塊協方差矩陣設置置零條件,從而提出了一種LCMV-CFAPC方法。仿真實驗和實測數據一致表明,該方法不需要對回波過采樣,不僅在采樣匹配情況下保持正常的脈壓性能,還可以在采樣失配情況下保持優于常規APC方法的穩健性,相比于常規MVDR-CFAPC方法,本文所提方法的性能也更加穩定。不過目前FAPC的耗時相比于傳統方法仍然較長,后期研究將著重于探索匹配濾波與FAPC相結合,進一步提高算法效率。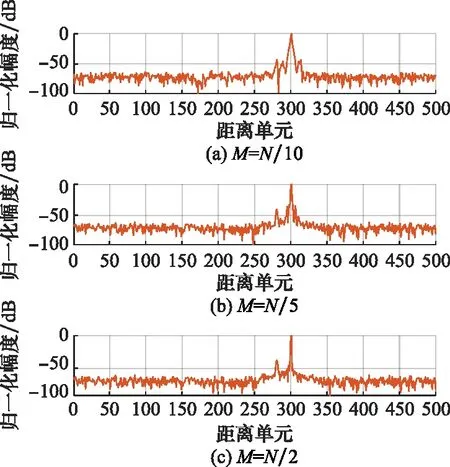
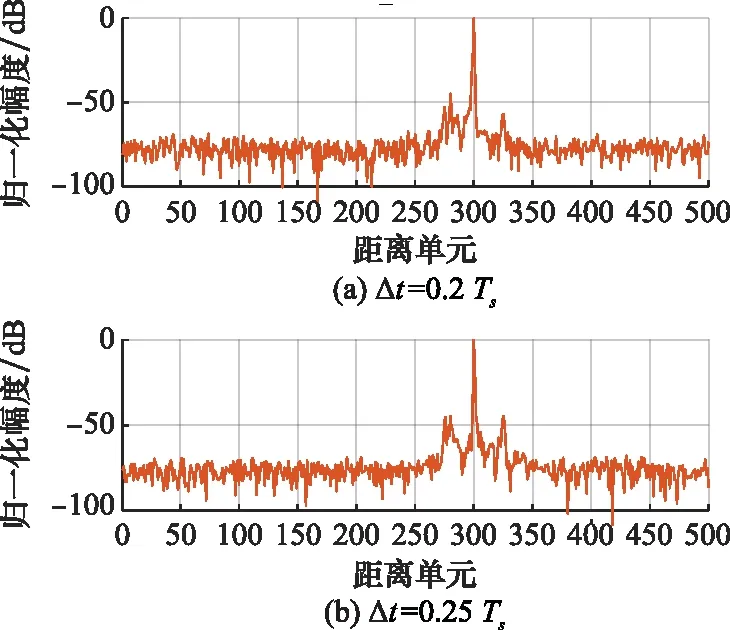
2.2 針對LFM信號脈壓的LCMV-CFAPC方法

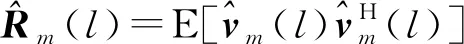
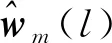
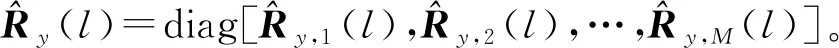
3 實驗分析
3.1 仿真場景下的方法性能對比

3.2 多目標采樣失配下的方法性能對比
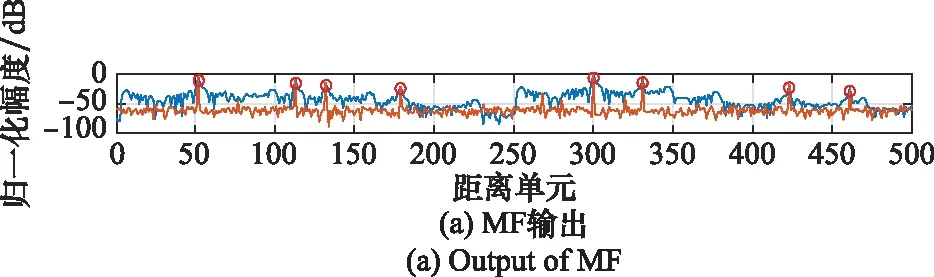
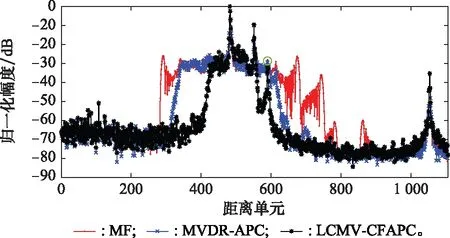
3.3 實測數據下的方法性能對比
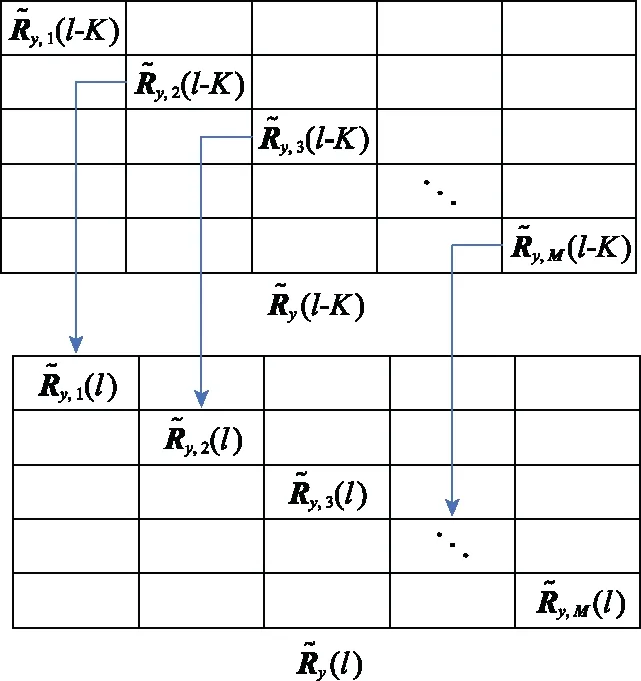
3.4 算法復雜度分析
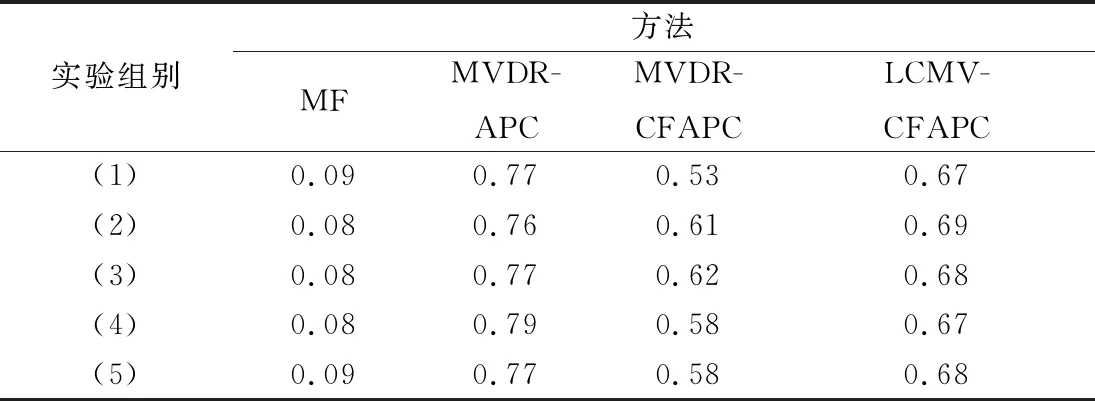


4 結 論

