網絡體系效能評估改進FDNA模型

邱祿蕓, 方志耕, 陶良彥, 陶秋澄

(南京航空航天大學經濟與管理學院, 江蘇 南京 211100)

0 引 言

信息技術的高速發展和廣泛應用使得復雜系統的集成、管理和評估問題愈發突出。現代戰爭中“聯合全域作戰(joint air defense operations, JADO)”、現代通訊中“天地一體化(sky-earth integration, SEI)”等進一步表現為“為了達成某種目標,由相互獨立又相互協作的一些系統組織在一起的更高層次的系統組合”,這種組合被稱為“體系”。體系概念經由Ackoff[1]的“一組集成的系統概念”,到Eisner等[2]的“體系內系統具有相互依賴性”,再到Maier[3]的“體系具備5項關鍵特性:組件系統的運行獨立性、管理獨立性、地理分布、涌現行為、進化性”而逐漸成熟。對體系效能做出準確評估是改進體系結構、優化指揮決策、完善行動控制的重要前提。而傳統的針對單一系統的效能評估方法無法滿足“巨系統”即體系的評估需求,亟待開展針對體系特性的新的效能評估研究。

目前,效能評估方法主要有數學解析法[4-5]、仿真分析法[6-7]、復雜網絡法[8-9]等類型。功能依賴網絡分析(functional dependency network analysis, FDNA)方法作為一種結合經驗的數學模型,可對體系內組件系統的依賴關系進行建模和度量。該方法最早產生于風險管理領域,由Garvey和Pinto為了研究因系統之間的依賴性引起的連鎖反應而提出[10-11]。在級聯失效的研究上,有別于Markov方法對失效傳遞給后續系統的概率進行建模[12-13],FDNA方法直接對依賴關系的失效影響進行建模。該方法基于圖論知識、馮·紐曼-摩根斯坦(von Neumann-Morgenstern, vNM)效用理論和風險管理最弱環規則(weakest link rule, WLR)展示了體系中組件系統的多層級依賴關系,體現了體系的“互聯互動”“松散耦合”等特性。Guariniello等對FDNA方法進行了完善,提出了“自主效能(self-effectiveness, SE)”[14]“數據可用性(availability of data, AOD)”[15]“依賴影響(impact of dependency, IOD)”[16]等概念,并應用于航空航天領域[17]。文獻[18]應用于金融網絡體系,文獻[19]應用于社交網絡體系,文獻[20]引入“降解指數(degradation index, DI)”用作局部依賴關系和全局關鍵節點的媒介,文獻[21]將依賴關系進一步區分為“使能依賴”和“增強依賴”。在國內,也有不少學者開展了相關研究。張旺勛等豐富了“絕對自主效能”和“相對自主效能”的概念[22-23],并應用于衛星導航體系[24]。文獻[25]引入“退化系數”,分析了裝備體系任務能力依賴性,文獻[26]研究了參數獲取的辦法,文獻[27]研究了依賴關系的波及效應。

分析研究現狀可知,以往的基于FDNA方法對體系效能進行評估存在以下不足:① 研究重點放在了對節點間的依賴關系分析上,而對效能結果作了單一性假設,這與實際不相符;② 沒有考慮組件系統的多態問題,雖對“自主效能”概念進行了探索性分析,但是只停留在概念的界定上,沒有考慮組件系統自主效能變化的內在邏輯,缺乏對組件系統是否存在多個狀態、狀態間是否以不同的速率進行轉移、不同狀態的效能衰減速度是否不同等問題的研究;③ 在進行體系效能評估時,沒有考慮體系內組件系統的重要度問題。文獻[14]雖也通過節點效能變化對其余節點的影響來識別關鍵節點,但其僅在主觀上依靠影響節點個數和數值范圍進行判斷,缺乏嚴密的邏輯推理和數學證明。

因此,在使用FDNA方法對網絡體系效能進行評估時,有以下改進要點:① 對體系效能進行評估,不能基于簡單系統“分解、靜態、孤立”的方式,必須用“整體、動態、依賴”的分析方法。體系是復雜動態環境衍生的技術框架[28],應構造包含時間變量的函數來了解、描述其演化過程;② 考慮組件系統的多態問題,基于組件系統狀態轉移的內在機理給出自主效能衰減函數的推理和自主效能衰減系數的定義,改進傳統FDNA方法中的計算表達式;③ 體系缺乏“可加性”,體系的效能值并非所有組件系統效能值的簡單相加[29]。應考慮組件系統對體系的影響,識別組件系統的重要性。最后,以文獻[14]提出的五節點航天網絡體系為例,驗證了所提方法的可行性。

1 網絡體系效能評估特性分析

在對網絡體系效能進行評估時,要綜合考慮以下幾組看似矛盾,實則辯證統一的特征。

1.1 獨立性及依賴性

Maier認為,組件系統的運行獨立性和管理獨立性是體系區別于系統的主要特征[3]。在單一系統內部,其各要素相互依存,無法實現獨立運行。但對于體系來說,其組件系統具備松散耦合的特點[30],其獨立運行時的效能變化對體系效能產生較大影響。因此,有必要將組件系統自主效能的變化作為一重要研究對象。

同時,體系是互相依賴的系統的集成[31],各組件系統之間存在上下游或其他邏輯的依賴關系,通過協作或交互方可提供體系完成任務所需的效能,必須考慮各節點間的依賴關系[32-33]。

1.2 動態性及穩態性

體系是不斷演化的,具備動態性,其效能評估會受到組件系統本身(如損毀率、修復率等狀態轉移強度參數)及其依賴關系(依賴強度、依賴關鍵度)等相關參數的影響。應該拋棄效能單一性假設,科學的評估不應當是一次性的,而是持續的、動態的監測。

同時,常見的體系內的組件系統往往是有限狀態,通過分析狀態的一步轉移概率,了解系統狀態的特性,建立穩態概率的方程等方式,通常可以求出穩態解,了解當時間趨于無窮時,體系效能的穩態情況。

1.3 不確定性及規律性

體系的定義有很多,但“不確定性”是諸多概念的共識。應當把體系及組件系統的效能本質上看作隨機變量,且網絡拓撲結構的特性注定會帶來級聯效應[34],引發不確定影響。

同時,體系雖具有“涌現性”,但對其效能評估開展研究時,應側重把握主要規律。例如,了解網絡體系的拓撲結構規律、了解組件系統的狀態轉移規律、了解組件系統的重要度排序規律等,對這些問題的回答能夠為發現體系的運行規律和揭示體系效能演化機理創造有利條件。

1.4 傳統FDNA模型的改進方向

根據傳統FDNA模型的簡要介紹及網絡體系效能評估的特性分析,可以對傳統FDNA模型針對體系進行效能評估時的優缺點及改進方向做簡要分析,如表1所示。“改進方向”為本文重點研究內容。

表1 傳統FDNA模型針對體系效能評估問題的優缺點

2 改進FDNA評估模型構建

2.1 網絡體系效能評估框架

評估過程分為5步:體系描述、組件系統的多態分析、FDNA方法的改進、組件系統的關鍵性識別、網絡體系效能的評估。具體如圖1所示。

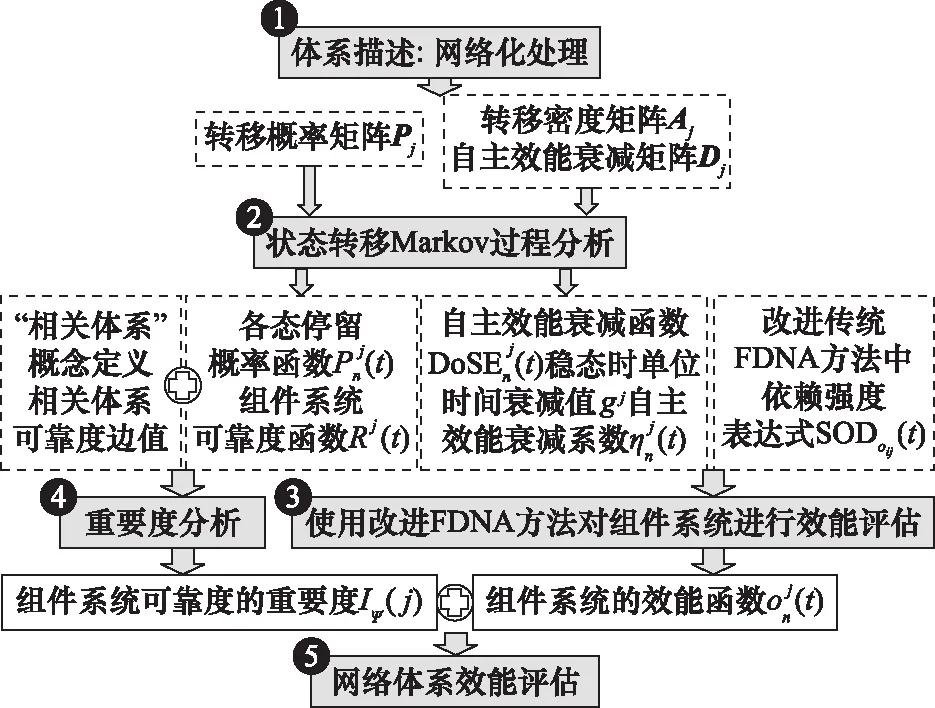
圖1 體系效能評估框架

(1) 體系描述

要對網絡體系進行效能評估首先需要明確評估對象。評估對象可以是聯合作戰體系、衛星通信體系等獨立系統之間、諸多系統與所處環境之間具備復雜關系、相互作用及深刻影響的體系。為把模糊、不確定的棘手問題簡化為清晰、明確的模型,應將體系中組件系統抽象成節點,組件系統之間的關系抽象成邊。

(2) 組件系統的多態分析

網絡體系內組件系統的特征在于運行和管理的獨立性,應重點考慮其自主效能的隨機特性。根據組件系統的失效情況劃分為不同狀態,輸入轉移概率矩陣,通過Markov過程分析,可得到組件系統在不同狀態下的停留概率函數,進而求得可靠度函數,為組件系統可靠度的重要度計算提供依據。

(3) FDNA方法的改進

為克服傳統FDNA方法中依賴強度表達式中的固定參數導致的效能計算不準確的問題,重點關注組件系統自主效能衰減機理,通過狀態轉移密度矩陣及自主效能衰減矩陣,推導出自主效能衰減函數及系數,為傳統FDNA方法中的依賴強度表達式的改進提供支撐。

(4) 組件系統的關鍵性識別

網絡體系中每個組件系統的可靠度不同,對體系的影響也不同。在對整個網絡體系效能進行評估時,必須要識別出組件系統的關鍵性。定義了“相關體系”的概念并求得可靠度,對組件系統的可靠度求偏導,得到組件系統的重要度。

(5) 網絡體系效能的評估

根據組件系統始于不同狀態時的自主效能衰減函數及重要度權重,求出整個網絡體系的效能函數。

2.2 組件系統的多態及效能衰減分析

假設在某體系中有k個組件系統,所有組件系統在任一時刻可以有w個狀態(如圖2所示,0態為最佳狀態,w態為完全失效狀態,其余為中間態)中的一個狀態。

圖2 組件系統的多態轉移示意圖

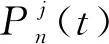
(1)

假設初始條件即t=0時,組件系統為0態,即

(2)

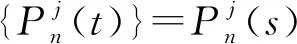
體系或組件系統會在運行過程中發生故障、磨損、老化、被攻擊乃至失效等的情況,組件系統的自主效能會發生下降,稱此現象為自主效能衰減(decline of self-effectiveness, DoSE),DoSE為一個分布在[-100,0]區間的、以utils為單位的數值。

當組件系統Nj具有以下轉移密度矩陣Aj及自主效能衰減矩陣Dj:

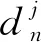
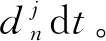
(3)

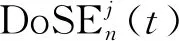
(4)

根據式(4)及矩陣Aj、Dj,可得

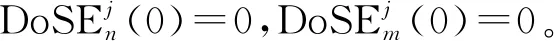
當t增大,組件系統Nj的自主效能平均衰減率為每小時1.43 utils,與初始狀態無關。當Nj開始于n態時,10小時后自主效能的衰減量為9.499 utils,當Nj開始于m態時,10小時后自主效能的衰減量為20.702 utils。

一般情況下,重視對長期穩態特性的分析,令組件系統Nj的自主效能衰減函數為

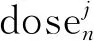
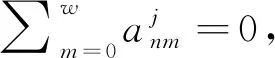
(5)

在式(5)兩端乘以組件系統各個狀態下的穩態概率和,得

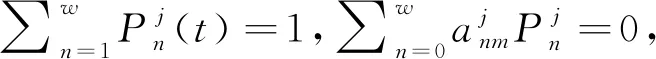
(6)

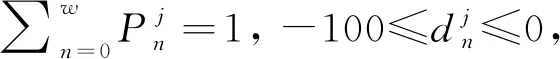
2.3 考慮效能衰減的模型參數改進

傳統FDNA方法結構如圖3所示,定義了接受節點與供給節點間兩類依賴關系:依賴強度(strength of dependency, SOD)和依賴關鍵度(criticality of dependency, COD),分別由α和β兩個參數表示,0≤α≤1,0 utils≤β≤100 utils。

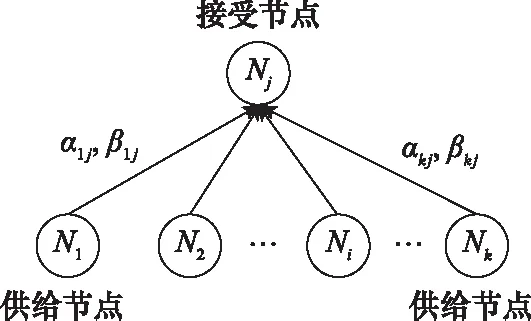
圖3 FDNA基本模型

圖3中,節點Nj的效能依賴于k個供給節點效能,即

Oj=Min(SODOj,CODOj)

(7)

其中:

(8)

傳統FDNA方法主要關注節點間的依賴關系及級聯效應,默認節點本身的效能為100 utils,即不考慮節點本身的效能變化。然而在如聯合作戰體系、衛星網絡體系等實際的體系環境中,普遍存在節點受到外界攻擊、干擾或內在磨損、故障等諸多非依賴性關系造成的效能減退影響的情況。因此,有必要考慮節點自身的效能衰減。Guariniello、張旺勛等均對“自主效能”開展了不同程度的研究,將其定義為“不考慮任何依賴關系時,節點自身的性能狀況”,為一個0到100的值。節點Nj的輸出性能由SODOj和CODOj兩部分共同決定,其中SODOj表示的是供給節點、依賴關系和接受節點自身共同作用對Nj的效能輸出;而CODOj表示的是供給節點和依賴關系對Nj的制約或限制,接受節點在該部分沒有貢獻。因而,學者多針對SODOj的表達式開展改進研究。Guariniello用SEj直接替代了SODOj計算公式中的“100”,雖考慮了接受節點的自主效能,卻較簡單粗暴,沒有考慮當自主效能極低時,依賴關系的有限性。張旺勛將接受節點的自主性能作為一個基礎,依賴關系基于此按比例發揮作用,但該方法未考慮節點自主效能的衰減性、隨機性,且將依賴強度速率設計為節點自主效能的比例關系,缺乏機理依據。

改進后的SODOij(t)的表達式如下:

(9)

基于圖4數據,根據Garvey[10]、Guariniello[14]、張旺勛[23]及本文提出的式(9),四者計算結果的對比如表2所示。

圖4 兩組件系統的依賴關系

表2 4種方法的對比

由表2可以看出,當接收節點正常,而供給節點效能降低時,前3種方法與本文方法在t=0時的計算結果相同,由于接收節點自主效能存在衰減現象,本文方法在t為5及10時,接收節點效能有不同程度的下降。當接收節點的自主效能降低時,Garvey方法不考慮此因素,默認接受節點只受供給節點影響,有明顯不足。Guariniello方法考慮了接受節點的自主效能,但仍有缺陷,如當接受節點完全失效,即SEj=0時,仍能通過依賴關系獲得高達90 utils的效能,顯然和實際情況相違背。張旺勛方法認為“接收節點是整個依賴關系的根本和基礎,而不僅僅是部分”,因而當接收節點完全失效時,即便受到供給節點的支持,效能仍為0 utils。本文方法認同張旺勛法思路,計算結果相同。但當接收節點與供給節點均有不同程度的下降時,張旺勛法將接受節點的效能下降速度設為自主效能的0.01倍,科學性有待考究,當供給節點效能為60 utils,接受節點自主效能為30 utils時,接受節點在依賴關系的影響下,降至19.2 utils,結果與常理不符,本文方法考慮了“供給節點效能高于接受節點自主效能,可以提供貢獻”,認為在t=0時,接受節點效能提升為57 utils,但受自主效能衰減影響,在t=10時,會降至37.83 utils。

2.4 組件系統的關鍵性識別

基于組件系統的多態分析、自主效能衰減機理分析以及改進的FDNA方法,可以求出單個組件系統在依賴關系的影響下的效能。為計算網絡體系的效能,充分考慮各個組件系統的特殊性,需識別組件系統的關鍵性。

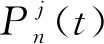
(10)

定理 2相關體系。若體系Ψ在組件系統xi(i=1,2,…,n)處為常量,即在所有(0i,X)上,Ψ(1i,X)=Ψ(0i,X),則第i個組件系統xi對于體系Ψ結構是不相關的,否則就是相關的。其中:

Ψ(0i,X)≡(x1,…,xi-1,0,xi-1,…,xn)

Ψ(1i,X)≡(x1,…,xi-1,1,xi-1,…,xn)

該定理的證明簡單,證明過程省略。該定理證明了相關體系中的每一組件系統都是不可或缺的。

定理 3體系結構函數的和式表達式。對于一切n階結構函數Ψ,所有的xi(i=1,2,…,n)皆有

Ψ(X)=xiΨ(1i,X)+(1-xi)Ψ(0i,X)

重復應用得

這個和式包含了所有n階的二值向量,約定00≡1。

定理 4相關體系被并聯、串聯體系的性質所界定。對任意階的相關系統Ψ(X)有：

證明在結構函數

中,若yj=1,有

或

對于對偶函數,亦有

即

或

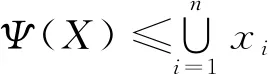
證畢

定理 5相關體系可靠度的邊值。令Ψ為一相關體系,在定理4的基礎上,很容易得到:

(11)

式(11)含義為:相關體系的可靠度被體系的割集與路集界定,高于割集而小于路集。

定理 6組件系統可靠度的重要度。體系內組件系統的可靠度不同,對體系造成的影響也不同。將體系中組件系統Nj的可靠度的重要度定義為

(12)

2.5 改進的網絡體系效能評估FDNA模型

在充分考慮網絡體系內各個組件系統的可靠度的重要度的基礎上,改進后的網絡體系效能評估FDNA模型如下所示：

組件系統的效能函數為

(13)

其中:

(14)

網絡體系的效能函數為

(15)

3 實例分析

以Guariniello和DeLaurentis提出的經典五節點航天網絡體系為例[14],該網絡包括地面設施(N1)、兩顆衛星(N2和N4)、一架無人機(N3)和一艘船(N5)。鏈接表示通信和數據依賴:衛星和無人機需要來自地面設施的數據,無人機也使用衛星導航,船從無人機和一顆衛星獲得數據。

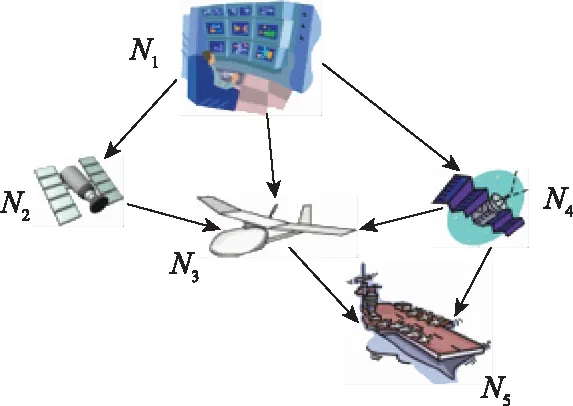
圖5 五節點航天體系

圖6 對應的FDNA模型及相關參數

設N1～N5的初始自主效能為90 utils、80 utils、95 utils、90 utils、75 utils。狀態轉移矩陣Pj分別為

3.1 組件系統的多態及效能衰減分析

由于組件系統N3既是接收節點又是供給節點,所處的網絡結構地位較特殊,因此以N3為例進行分析。根據PN1、式(1)、式(2),可得該組件系統在各態的停留概率時間函數：

圖7 組件系統N3在各狀態的停留概率函數

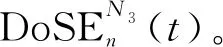
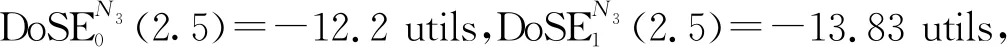
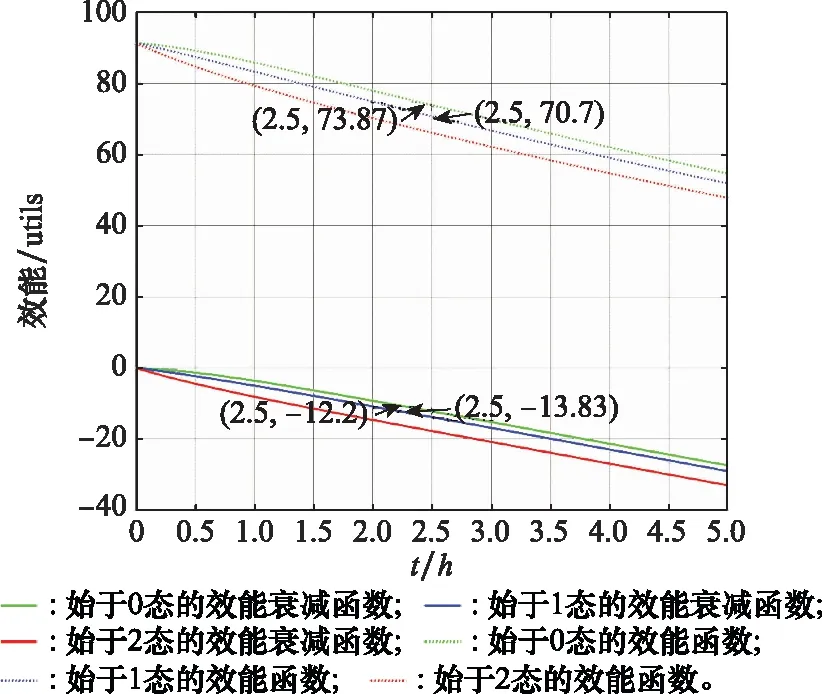
圖8 組件系統N3的自主效能衰減曲線與效能曲線

根據式(6)可求得穩態時,該組件系統單位時間效能衰減期望值,其他組件系統的計算類似。表3為該體系內5個組件系統(假設均始于0態)的重要效能參數對比,包括自身效能、效能衰減量(t=2)、不考慮依賴關系的效能值(t=2)、考慮依賴關系的效能值(t=2)、單位時間效能衰減期望值(穩態)。

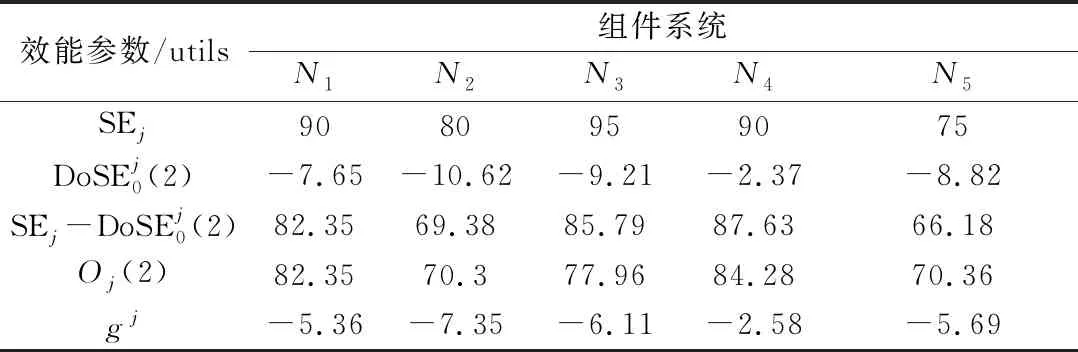
表3 組件系統的重要效能參數對比

據表3數據的第3行(僅考慮自身效能衰減時的效能)和第4行(既考慮自身效能衰減又考慮節點間依賴關系的效能)可知,N1作為供給節點,效能僅與自主效能衰減值有關,不受依賴關系影響。N2與N5由于自主效能較低,接受了來自于供給節點的數據支撐,使得效能值在自主效能衰減的基礎上,略有所提升。N3與N4的供給節點自主效能衰減較大,使得此二節點的效能值在自主效能衰減的基礎上,受依賴關系制約,略有下降。穩定狀態時,單位時間自主效能衰減量最大的是N2,最小的是N4,可以為運行期間的維修策略提供數據參考,例如加強對N2的維修保養或做好備件供應。

3.2 可靠度的重要度分析及體系效能評估

該網絡體系的最小路集為{N1,N2,N3,N5}, {N1,N4,N3,N5}, {N1,N3,N5}, {N1,N4,N5},最小割集為{N1}, {N5}, {N3,N4}。由式(11)可得下界(3個最小割集先并后串組成的結構)和上界(4個最小路集先串后并組成的結構),等效結構圖如圖9所示。

圖9 體系的等效結構圖

根據式(12),對于組件系統Ni的重要度IΨ(Ni)有:

將相關參數代入計算,可得各組件系統的重要度區間。再根據式(13)～式(15),可得組件系統始于不同狀態時,網絡體系效能的上下界限的演化情況,如圖10所示。圖10中,紅色、藍色、黃色區域分別為組件系統始于0態、1態、2態時的網絡體系效能區間,整體隨時間變化呈下降趨勢。t=5時,始于0態的體系效能區間為[59.92, 66.77],始于1態的體系效能區間為[56.28, 63.2],始于2態的體系效能區間為[53.23, 60.81]。3個區域高度按0態、1態、2態遞減且有所重疊,符合網絡體系內組件系統的多態轉移及效能衰減特征。

圖10 體系效能上下界曲線

4 結 論

本文的3項重點工作為:① 研究了網絡體系內組件系統的自主效能衰減機理。開展了Markov過程分析,提出了自主效能衰減函數及系數的概念,給出了相關公式和推導過程,優化了傳統FDNA方法中依賴強度的表達式,克服了傳統方法默認“自主效能為固定參數100 utils”及“自主效能一成不變”的缺陷;② 計算了組件系統可靠度的重要度。界定了“相關體系”“相關體系可靠度的邊值”等概念,考慮了不同組件系統對體系的影響力,給出了網絡體系效能的評估公式;③ 以經典五節點航天網絡體系為例,進行了模型驗證。可以為聯合作戰體系、衛星網絡體系等類似網絡體系提供效能評估與預測、重要節點識別、運行管理與維修等的現實問題的數據支撐與策略參考。

該方法在對網絡體系進行效能評估時,可以較好地兼顧體系“獨立性及依賴性”“動態性及穩態性”“不確定性及規律性”等的特性,發揮傳統FDNA在分析體系中依賴關系的優勢,克服傳統方法存在的忽視組件系統的運行獨立性、未考慮體系層面、效能結果單一性假設等缺點。構建的網絡體系效能評估改進FDNA模型可以為類似的評估工作提供一定的參考價值。