網絡化多傳感器-多武器協同防空任務規劃

董 晨, 帥逸仙, 周金鵬, 賴 鵬, 程仙壘

(1. 上海機電工程研究所, 上海 201109; 2. 軍事科學院系統工程研究院, 北京 100101)

0 引 言

空中威脅和軍事技術的發展促使防空體系向網絡化方向演化[1],以協同作戰能力(cooperative engagement capability, CEC)為核心的海軍一體化火力控制-制空(naval integrated fire control-counter air, NIFC-CA)[2]、陸軍一體化防空反導(integrated air and missile defense, IAMD)[3]是上述體系的代表,這些體系以網絡為中心,各要素互聯互通、分散部署,提升整體作戰能力。近年來出現的馬賽克戰[4]概念更加強調以分布式作戰管理取代集中式指揮控制,利用動態、協調和具有高度自適應性的可組合力量,提升生存能力[5]。

通過對典型網絡化防空體系的研究發現,對體系各組成要素的任務進行合理規劃與控制,能夠顯著提升體系的防空效能。傳感器、武器等要素的協同是其中的重要部分,基于通用的算法和共享的戰術數據,在多個分散的平臺上同時產生相同的決策,形成不同平臺傳感器、武器的協同計劃,可實現多傳感器對目標的接力跟蹤、跨平臺的傳感器到武器打擊引導、多武器對目標的協同抗擊,因此網絡化多傳感器-多武器協同防空任務規劃應作為重點問題開展研究。

目前,針對多傳感器資源管理、協同跟蹤等問題,以探測精度最高、協同探測效能最大等為目標,形成多傳感器的協同探測計劃,保證探測任務有序執行[6-13]。針對多武器火力規劃、動態武器-目標分配等問題,以最小化發射時間、最大化攔截效益等為目標,形成武器-目標分配方案[14-21]。針對網絡化作戰條件下防空火力分配,對目標-制導節點-火力節點間的優化匹配問題開展研究[22],提出協同制導體制下的武器運用決策方法[23]及武器通道組織模型[22]。此外,文獻對網絡化條件下的“目標-傳感器-武器”匹配問題進行研究,實現某一時刻或階段上的探測、火力資源最優分配[21-24]。但是,對多傳感器-多武器協同任務規劃有待進一步研究,這一問題在“目標-傳感器-武器”匹配的基礎上,要求在交戰全過程中對傳感器跟蹤時段、武器攔截時段進行合理規劃,避免作戰資源在時間上的沖突,使對目標的跟蹤時間滿足武器制導需求,且防空效能最優化,最終形成以“目標-傳感器及跟蹤時段-武器及攔截時段”表示的多傳感器-多武器協同交戰計劃,這增加了問題的復雜程度。

針對上述問題,本文提出網絡化多傳感器-多武器協同防空任務規劃方法。考慮任務要求、裝備性能、運用限制等約束,構建多武器攔截與多傳感器跟蹤任務規劃模型,前者以攔截時刻最早或次數最多為目標,輸出武器-目標配對、攔截時段及跟蹤時間要求,后者以滿足跟蹤時間要求為目標,輸出傳感器-目標配對及跟蹤時段。設計基于時段優選拼接和分支定界法的多傳感器-多武器協同任務規劃算法,通過武器攔截時段優選加多步傳感器跟蹤時段優選與拼接,形成多傳感器-多武器協同交戰計劃,支持多傳感器接力跟蹤、跨平臺打擊引導、多武器協同抗擊。假定預警機支援下的艦艇編隊協同防空場景,設置多種威脅目標及攔截任務,驗證本文提出方法的有效性。

1 問題描述

以NIFC-CA為例,對于由艦艇、預警機、戰斗機等組成的任務群,各平臺通過CEC網絡實時共享數據,基于通用的算法開展多傳感器-多武器協同防空任務規劃,為來襲目標規劃最優的防空武器及攔截時段,實現多武器對目標的協同抗擊,滿足期望的攔截效果,同時為目標規劃最優的傳感器(或傳感器序列)及跟蹤時段,使對目標的跟蹤時間滿足武器攔截目標的制導需求,實現多傳感器對目標的接力跟蹤以及跨平臺的傳感器到武器打擊引導。

為不失一般性,在后續研究中假設任務群由多個作戰平臺組成,通過指揮控制系統對m部具備跟蹤制導功能的傳感器和n部艦空導彈武器系統組網管理,且已獲得p個最具威脅的來襲目標信息,估計目標的航跡。

2 協同任務規劃方法

2.1 規劃信息

作為網絡化多傳感器-多武器協同任務規劃的輸入,定義以下的規劃信息。

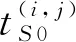
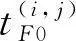
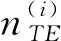
2.2 任務規劃模型

將網絡化多傳感器-多武器協同防空任務規劃分解為相關聯的多武器攔截和多傳感器跟蹤兩部分,分別構建任務規劃模型。多武器攔截任務規劃模型用于在多約束條件下尋找最佳的武器-目標配對,規劃對目標的攔截時段并提出跟蹤時間要求。多傳感器跟蹤任務規劃模型用于在多約束條件下尋找最佳的傳感器-目標配對,規劃對目標的跟蹤時段,盡可能滿足對目標的跟蹤時間要求。通過上述配對,可將不同平臺的武器和傳感器通過目標關聯起來,實現跨平臺打擊引導等網絡化作戰模式。

2.2.1 多武器攔截任務規劃模型

多武器攔截任務規劃是在多約束條件下,根據對不同類型目標的攔截要求,優化多平臺的武器攔截時段,形成多部武器對多批目標的協同攔截計劃,并根據武器對目標的攔截時段提出跟蹤時間要求。該問題對應的優化模型如下:

(1)

s.t.

-DF*TF0≤0

(2)

DF·I-NFR≤0

(3)

I·DF-I=0

(4)

NTE-I·(DF*NF)≤0

(5)

式中:0與I分別為合適維的零向量和單位向量;*為兩個同維矩陣或向量的相同行列元素相乘。

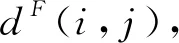
(6)

(7)

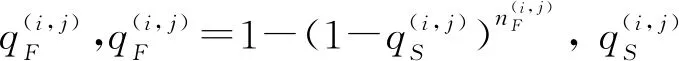
式(2)與式(3)為武器能力約束,分別代表武器對目標具備攔截條件以及攔截能力。式(4)為武器運用約束,代表對任一目標都應分配一部武器進行射擊,避免目標漏防,同時也避免多部武器同時射擊一個目標導致彈藥浪費。式(5)為任務要求約束,代表對各目標的射擊次數不應少于期望射擊次數。

設式(1)～式(5)優化問題的解為DFO,則規劃的對目標的起始交戰時刻向量TE0和終止交戰時刻向量TEf,TE0、TEf∈Rp均為行向量,有

TE0=I·(DFO*TF0)

(8)

TEf=I·(DFO*TFf)

(9)

TE0和TEf的第i個元素tE0(i)和tEf(i)分別代表規劃的對第i個目標的起始交戰時刻和終止交戰時刻。

為滿足武器攔截目標的跟蹤時間要求,需要在武器與目標交戰之前使傳感器跟蹤目標并為武器提供引導,起始引導時刻與起始交戰時刻之間需留出武器的準備時間,在武器與目標交戰之后結束跟蹤目標并終止引導。定義起始引導時刻向量TG0和終止引導時刻向量TGf,TG0、TGf∈Rp為行向量,其第i個元素tG0(i)、tGf(i)分別代表對第i個目標的起始引導時刻和終止引導時刻,有

TG 0=TE0-TFP·DFO

(10)

TGf=TEf

(11)

2.2.2 多傳感器跟蹤任務規劃模型

多傳感器跟蹤任務規劃是在多約束條件下,優選多平臺的傳感器跟蹤時段,形成多部傳感器對多批目標的協同跟蹤計劃,使傳感器對目標的跟蹤時段滿足武器攔截任務規劃提出的跟蹤時間要求。該問題對應的優化模型如下:

(12)

s.t.

-DS*TS 0≤0

(13)

DS·I-I≤0

(14)

I·DS-I=0

(15)

I·(DS*TS 0)-TG 0≤0

(16)

TG 0-I·(DS*TSf)<0

(17)

TSAf*(DS·I)-(DS*TS 0)·I<0

(18)

式(12)中,矩陣DS∈Nm×p為優化變量,其元素非0即1,記其第i行第j列元素為dS(i,j),僅當dS(i,j)=1時代表分配第i個傳感器跟蹤第j個目標。JS為優化目標,有

(19)

式(19)代表對目標的跟蹤時間最大程度滿足跟蹤時間要求。其中, | 定義為兩個同維矩陣或向量的相同行列元素相除。

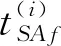
設式(12)～式(18)優化問題的解為DS O,則規劃的對目標的起始跟蹤時刻矩陣TT0和終止跟蹤時刻矩陣TTf,TT0、TTf∈Rp均為行向量,為節約傳感器資源且滿足任務要求約束,有

TT 0=max{I·(DS O*TS 0),TG 0}

(20)

TTf=min{I·(DS O*TSf),TGf}

(21)

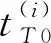
2.3 規劃算法設計

武器攔截任務規劃和傳感器跟蹤任務規劃是NP(non-deterministic polynomial)-complete問題[25],這類問題可由粒子群算法、退火算法、遺傳算法等智能優化算法求解[26-31],但這類算法的隨機性、近似性不能保證在多個分散的作戰平臺上產生相同的決策,因此需采用精確算法求解網絡化多傳感器-多武器協同防空任務規劃問題。而且本文研究的網絡化多傳感器-多武器協同防空任務規劃主要解決戰術/火力層面的作戰資源協調問題,問題的規模有限,采用精確算法能在可接受的時間內求得最優解。

本文設計基于時段優選拼接和分支定界法的多傳感器-多武器協同任務規劃算法,基于多武器攔截任務規劃模型和多傳感器跟蹤任務規劃模型,通過武器攔截時段優選加多步傳感器跟蹤時段優選與拼接,實現網絡化多傳感器-多武器協同防空任務規劃。算法流程圖如圖1所示。

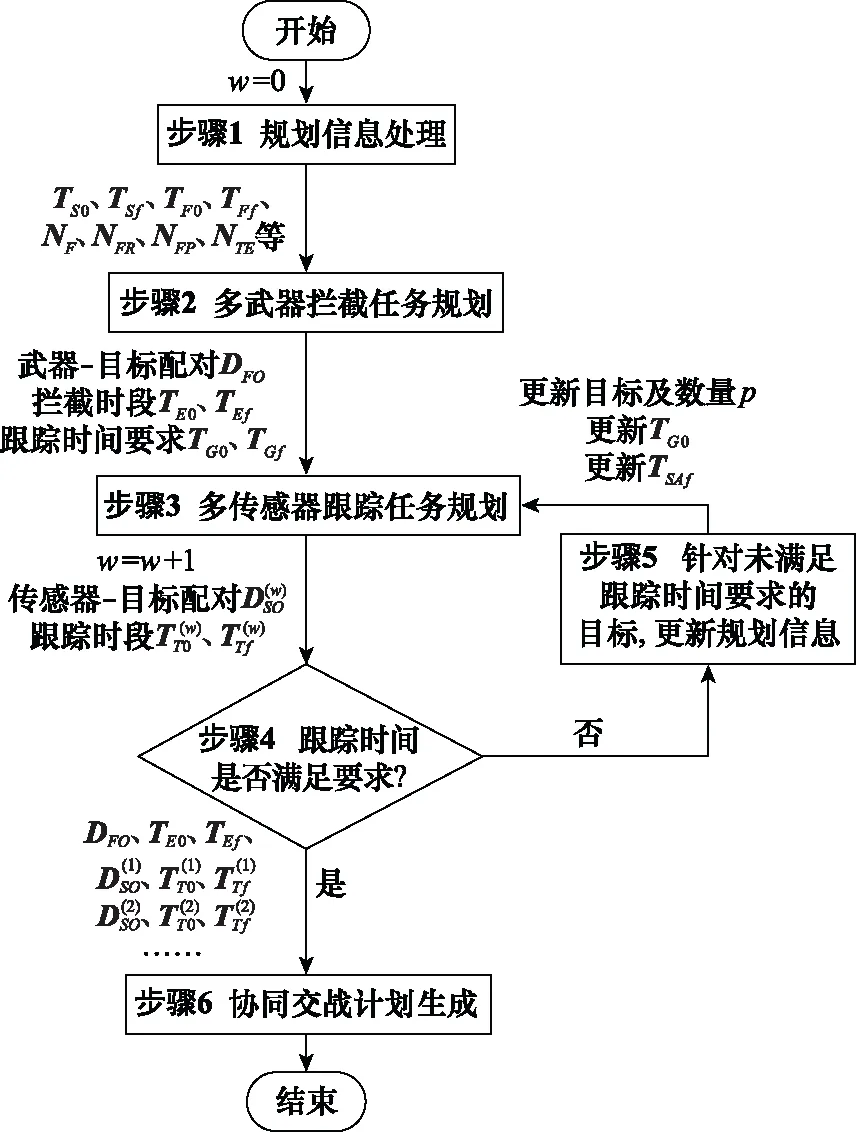
圖1 算法流程圖

算法將網絡化多傳感器-多武器協同防空任務規劃分解為步驟2的多武器攔截任務規劃和步驟3～步驟5的多步多傳感器跟蹤任務規劃兩個主要部分,對問題進行解耦。在第一部分,優選武器攔截時段,形成對目標的攔截計劃,并計算對目標的跟蹤時間要求;在第二部分,根據跟蹤時間要求,優選傳感器跟蹤時段,盡可能滿足對目標的跟蹤時間要求,若一次規劃未滿足要求,則更新多傳感器跟蹤任務規劃模型,再次優選傳感器跟蹤時段,直至跟蹤時間要求滿足為止,對前述多次規劃得到的傳感器跟蹤時段進行拼接,形成對目標的跟蹤計劃。最后,依靠步驟6的協同交戰計劃生成,形成多傳感器-多武器協同交戰計劃。該算法的具體步驟如下。

步驟 1規劃信息處理。根據目標信息、裝備信息、任務要求等生成規劃信息,包括TS 0、TSf、TF0、TFf、NF、NFR、TFP、NTE等。

步驟 2多武器攔截任務規劃。建立式(1)～式(5)所示的多武器攔截任務規劃模型,采用分支定界法計算最優解DFO,按式(8)和式(9)計算TE0、TEf,并按式(10)和式(11)計算TG 0、TGf。

步驟 3多傳感器跟蹤任務規劃。建立式(12)～式(18)所示的多傳感器跟蹤任務規劃模型,采用分支定界法計算最優解DS O,按式(20)和式(21)計算TT 0、TTf。

步驟 4跟蹤時間要求滿足判斷。將DS O代入式(19)中的DS,計算JS;若JS<1,說明步驟3得到的多傳感器跟蹤計劃不滿足跟蹤時間要求,轉步驟5;若JS≥1,則跟蹤時間要求已滿足,轉步驟6。

步驟 5規劃信息更新。按下式計算對各目標的跟蹤制導時間滿足程度,定義向量Q∈Rp。

Q=[I·(DS O*TSf)-TG 0]|(TGf-TG 0)

(22)

Q的第i個元素q(i)代表對第i個目標的跟蹤制導時間滿足度,若q(i)<1,則對第i個目標的跟蹤時間不滿足跟蹤時間要求;針對全部未滿足跟蹤時間要求的目標:

步驟5.1目標數更新,按照未滿足跟蹤時間要求的目標的數量更新p值;

步驟5.2起始引導時刻更新,假設對第i個目標,其起始引導時刻tG0(i)更新為

tG0(i)=tTf(i)-δ

(23)

式中:tTf(i)為步驟3規劃的對第i個目標的終止跟蹤時刻,δ為兩部傳感器接力跟蹤目標的交班過渡時間;

步驟5.3傳感器工作狀態更新,對步驟3已分配跟蹤任務的傳感器,依據該傳感器對目標的終止跟蹤時刻更新TSAf中的相應元素;

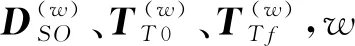
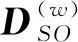
3 規劃示例

假設3艘驅逐艦在1架預警機支援下執行對空防御任務,在此場景下驗證本文提出的方法,檢驗規劃結果是否滿足前述約束并實現了優化目標。

3.1 任務場景1(攔截轟炸機群)

3.1.1 條件假設

假設有6批轟炸機以300 m/s的速度從方位角90°的扇面內對3艘驅逐艦實施突擊。設驅逐艦可同時跟蹤并攔截10批目標,預警機可同時跟蹤20批目標,假設各驅逐艦為不暴露自身位置,艦載雷達不開機,依靠預警機探測信息引導各驅逐艦艦空導彈攔截轟炸機。將目標編號為T1～T6,作戰平臺、傳感器及武器編號如表1所示。

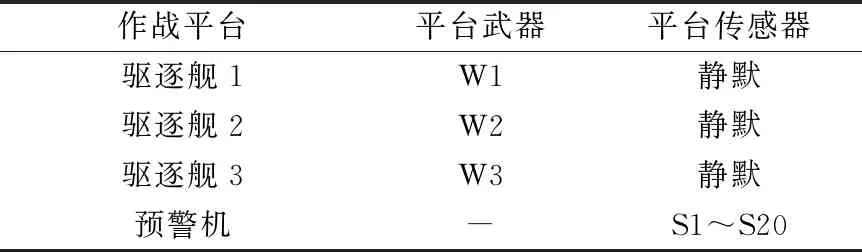
表1 場景1作戰平臺、傳感器、武器的編號

3.1.2 算法參數

依據假設條件,算法的參數及其取值如下:目標數量p=6,武器數量n=3,傳感器數量(含虛擬傳感器)m=20,武器對目標的起始交戰時刻矩陣TF0中各元素和終止交戰時刻矩陣TFf中各元素取值如表2所示,攔截機會矩陣NF中各元素取值如表3所示,武器攔截能力向量NFR中各元素均為10,武器交戰準備時間向量TFP中各元素均為30 s,期望射擊效果向量NTE中各元素均為4,傳感器對目標的起始跟蹤時刻矩陣TS 0中各元素均為1 s,終止跟蹤時刻矩陣TSf中各元素均為300 s,兩部傳感器接力跟蹤目標的交班過渡時間為5 s。

表2 武器對目標的攔截時段(場景1)

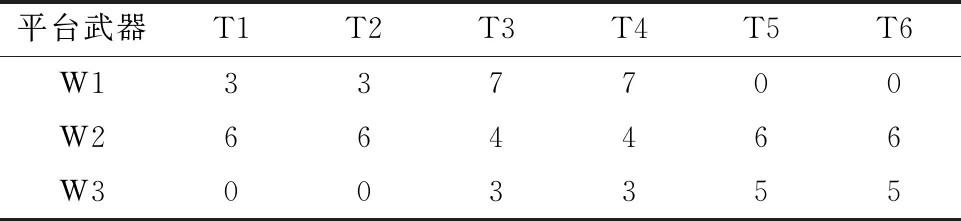
表3 武器對目標的攔截機會(場景1)

3.1.3 規劃結果

以平均攔截時刻最早為目標規劃多傳感器-多武器協同交戰計劃,結果如圖2所示。在Intel i3處理器、4G內存PC機上,利用Matlab 7.6.0軟件完成規劃耗時1.02 s。圖2(a)中,橫坐標為時間軸,縱坐標為目標軸,有T1～T6共6個目標。紅色實線為規劃的武器對目標的攔截時段,執行攔截任務的武器編號W1～W3標注在相應的紅線中部。藍色實線為規劃的傳感器對目標的跟蹤時段,執行跟蹤任務的傳感器編號S1～S20標注在相應的藍線中部。由圖2(a)可見,對各目標均分配了武器進行攔截,對目標T1～T6的攔截機會分別為6、6、4、4、5、5,滿足對各目標攔截次數不少于4次的要求,平均攔截機會為5次,對目標的平均交戰起始時刻為75 s。對各目標均分配傳感器進行跟蹤,對各目標的持續跟蹤時間滿足武器作戰要求,即對一個目標,規劃的跟蹤時段比攔截時段提前30 s開始、規劃的跟蹤時段與攔截時段同時結束。圖2(b)中,驅逐艦以黑色方框表示,預警機以黑色圓圈表示,紅虛線代表對目標飛行航線的攔截部分,藍實線代表對目標飛行航線的跟蹤部分。

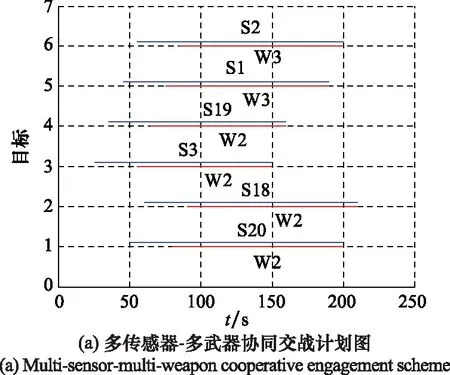
圖2 場景1下的規劃結果(攔截時機優化)

結合表1和圖2,可形成如表4所示的多傳感器-多武器協同交戰計劃。

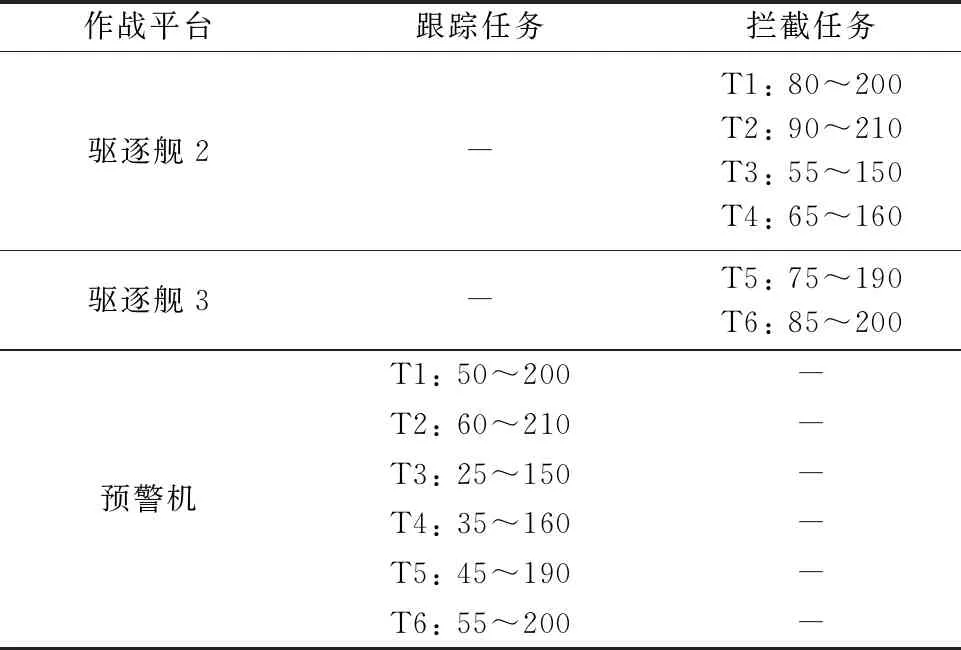
表4 場景1下的協同作戰計劃

作為對比,以平均攔截機會最大為目標規劃多傳感器-多武器協同交戰計劃,結果如圖3所示。各項約束條件均滿足,對目標T1～T6的攔截機會分別為6、6、7、7、6、6,平均攔截機會增加到6.3次,對目標的平均交戰起始時刻則延后到95 s。

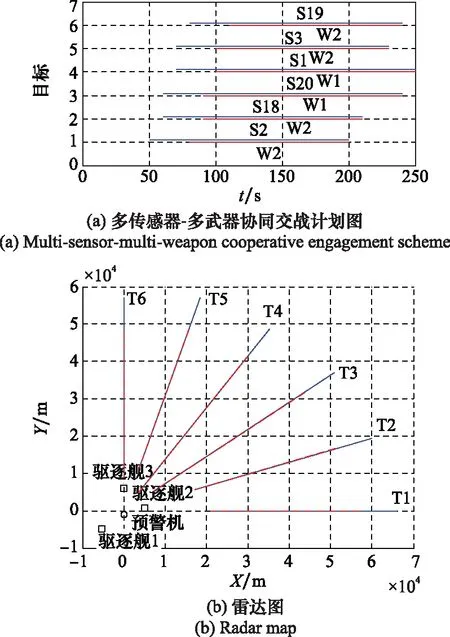
圖3 場景1下的規劃結果(攔截機會優化)

對比上述兩種優化目標下的規劃結果可見,算法分別實現了對攔截時機和攔截機會的優化,且武器和傳感器裝備能力、裝備運用、任務要求等約束均得到滿足。

3.2 任務場景2(抗擊反艦導彈群)

3.2.1 條件假設

假設有24批反艦導彈以250 m/s的速度從方位角270°的扇面內對3艘驅逐艦實施攻擊。設驅逐艦可同時跟蹤并攔截10批目標,預警機可同時跟蹤20批目標。將目標編號為T1～T24,作戰平臺、傳感器及武器編號如表5所示。

表5 場景2作戰平臺、傳感器、武器的編號

3.2.2 算法參數

依據假設條件,算法的參數及其取值如下:目標數量p=24,武器數量n=3,傳感器數量(含虛擬傳感器)m=50,武器對目標的起始交戰時刻矩陣TF0中各元素和終止交戰時刻矩陣TFf中各元素取值如表6所示,攔截機會矩陣NF中各元素取值如表7所示,武器攔截能力向量NFR中各元素均為10,武器交戰準備時間向量TFP中各元素均為30 s,期望射擊效果向量NTE中各元素均為5,傳感器對目標的起始跟蹤時刻矩陣TS 0中各元素和終止跟蹤時刻矩陣TSf中各元素取值如表8所示,兩部傳感器接力跟蹤目標的交班過渡時間為5 s。

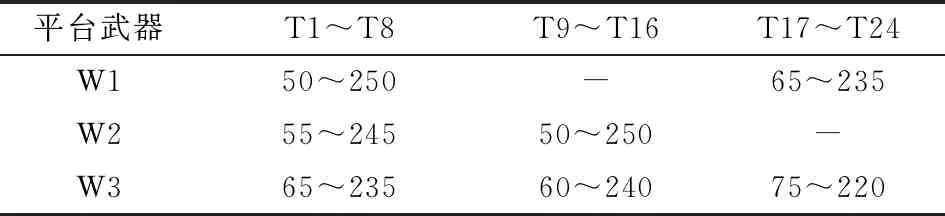
表6 武器對目標的攔截時段(場景2)

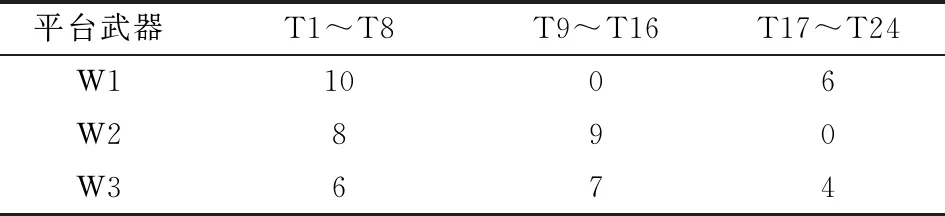
表7 武器對目標的攔截機會(場景2)

表8 傳感器對目標的跟蹤時段

3.2.3 規劃結果

以平均攔截機會最大為目標規劃多傳感器-多武器協同交戰計劃,結果如圖4所示。在與任務場景1相同的計算條件下,完成規劃耗時3.04 s。

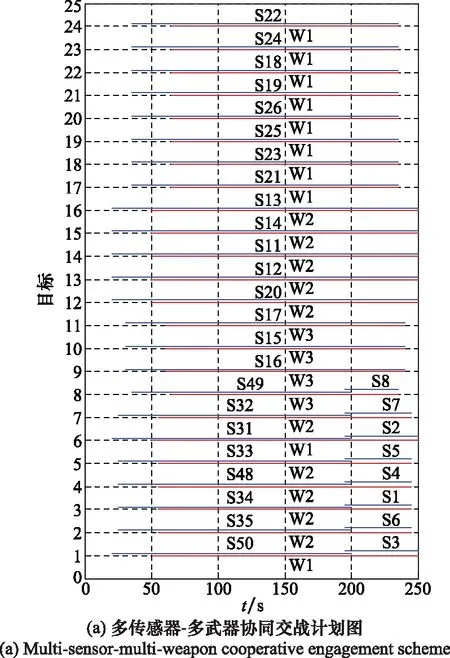
圖4 場景2下的規劃結果(攔截機會優化)

圖4(a)中,橫坐標為時間軸,縱坐標為目標軸,有T1～T24共24個目標。紅色實線為規劃的武器對目標的攔截時段,執行攔截任務的武器編號W1～W3標注在相應的紅線中部。藍色實線為規劃的傳感器對目標的跟蹤時段,執行跟蹤任務的傳感器編號S1～S50標注在相應的藍線中部。由圖4(a)可見,對各目標均分配了武器進行攔截,對各目標的攔截機會分別為T6和T8各10次、T13～T16各9次、T1～T5和T7各8次、T9～T12各7次、T17～T24各6次,滿足對各目標攔截次數不少于5次的要求,平均攔截機會達到7.5次。對各目標均分配傳感器進行跟蹤,其中對目標T1～T8的跟蹤是由屬于不同平臺的傳感器接力完成的,交班過渡時間滿足5 s的要求,對各目標的持續跟蹤時間滿足武器作戰要求,即對一個目標,規劃的跟蹤時段比攔截時段提前30 s開始、規劃的跟蹤時段與攔截時段同時結束。圖4(b)中,驅逐艦以黑色方框表示,預警機以黑色圓圈表示,位置同圖3(b);紅虛線代表對目標飛行航線的攔截部分,藍實線代表對目標飛行航線的跟蹤部分。

結合表6和圖4,可形成如表9所示的多傳感器-多武器協同交戰計劃。

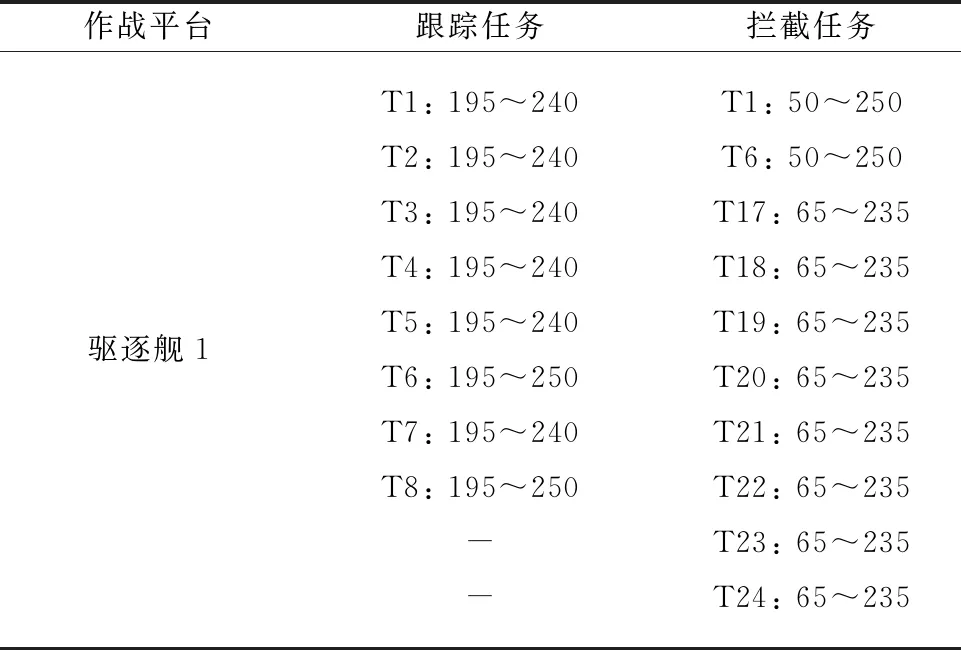
表9 場景2下的協同作戰計劃

續表9

作為對比,將驅逐艦2的探測能力減弱,壓縮其對目標的探測遠界,從而延后其對目標的起始跟蹤時刻,更新后的傳感器對目標的起始跟蹤時刻矩陣TS 0中各元素和終止跟蹤時刻矩陣TSf中各元素取值如表10所示,其他參數保持不變,以平均攔截機會最大為目標規劃多傳感器-多武器協同交戰計劃,結果如圖5所示。各項約束條件仍滿足,由于驅逐艦2對目標的起始跟蹤時刻延后,對T9～T16的跟蹤計劃發生較大變化,由原驅逐艦2獨立跟蹤,變為由預警機負責200 s之前的跟蹤任務,之后由驅逐艦2負責對T9、T10、T13～T16接力跟蹤,由驅逐艦3負責對T11、T12接力跟蹤,交班過渡時間仍滿足5 s的要求。最終對目標的跟蹤和攔截效果與圖4(b)相同,這里不再重復繪制雷達圖。

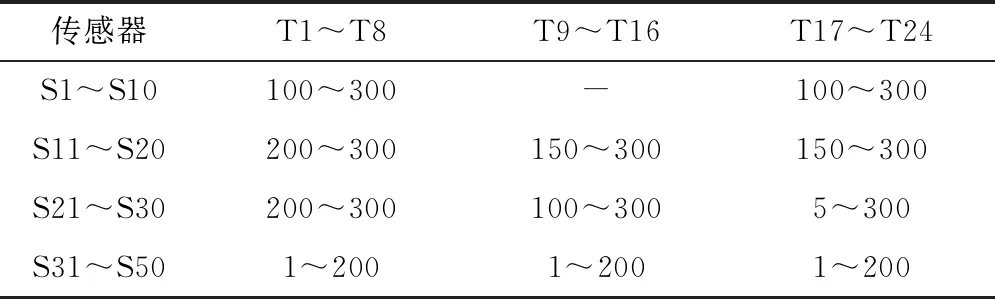
表10 場景2下傳感器對目標的跟蹤時段

圖5 場景2下的規劃結果(攔截機會優化,驅逐艦2探測能力削弱)

由上述兩種情況下的規劃結果可見,算法實現了對攔截時機的優化,武器和傳感器裝備能力、裝備運用、任務要求等約束得到滿足,特別是在部分傳感器能力下降的情況下,調度其他傳感器資源進行補充,保證了對目標的跟蹤時間滿足要求。

4 結 論

本文對網絡化多傳感器-多武器協同任務規劃方法進行研究,建立多武器攔截與多傳感器跟蹤任務規劃模型,設計基于時段優選拼接和分支定界法的多傳感器-多武器協同任務規劃算法,能以對目標的攔截機會最多或攔截時機最早、跟蹤時段滿足跟蹤時間要求為目標,在滿足武器和傳感器裝備能力、裝備運用、任務要求等約束的條件下,生成“目標-傳感器及跟蹤時段-武器及攔截時段”表示的多傳感器-多武器協同交戰計劃。在假設的艦艇編隊與預警機協同防空場景下,設置攔截轟炸機群、反艦導彈群兩類任務,分別驗證本文提出的方法,規劃結果均滿足各項約束條件并實現了優化目標,該方法是有效的。

本文的規劃算法在較小規模的多傳感器-多武器協同防空任務規劃上具有良好的應用潛力,也適用于裝備論證仿真等對實時性要求不高的大規模應用場景。若在一個集中式指揮節點上進行運算,則可用粒子群算法、遺傳算法等智能優化算法代替分支定界法,提高規劃算法的時效性,更好地適應大規模規劃問題。在后續研究中,需提升精確算法的時效性,以滿足分布式指揮對求解精確性的要求和大規模規劃問題對求解時效性的要求。