MIMO雷達稀疏陣列優化設計方法

唐軍奎, 劉 崢,*, 謝 榮, 曾 波

(1.西安電子科技大學雷達信號處理國家重點實驗室, 陜西 西安 710071;2. 華東電子工程研究所, 安徽 合肥 230088)

0 引 言

多輸入多輸出(multiple input multiple output,MIMO)雷達指的是各個發射陣元發射不同波形信號,多個接收天線接收的雷達系統。這種信號發射的波形分集使得MIMO雷達在空間分辨率、參數識別能力、低速目標檢測等方面比一般相控陣雷達具有更好的性能,成為了近幾年雷達界的研究熱點[1-7]。MIMO雷達的發射和接收均為多陣元的陣列結構,不同的陣列設計對系統性能具有顯著影響。因此,在陣列結構復雜度一定的條件下對MIMO雷達進行稀疏陣列優化,提高其系統的檢測與定位等能力至關重要[8-12]。

對目標的角度測量是雷達系統的基本功能之一。傳統相控陣雷達中的角度估計方法同樣適用于MIMO雷達[13-19],單脈沖測角方法因其實現比較簡單、測角精度高、抗干擾能力強等優點,在雷達系統中得到了廣泛應用。文獻[14]利用全微分方法對MIMO雷達和相控陣雷達測角精度進行了詳細的推導和分析。文獻[17]對相控陣雷達和MIMO雷達的單脈沖比幅、比相測角方法進行了對比分析。這些單脈沖測角技術的研究都表明MIMO雷達可以利用發射孔徑自由度提高其參數估計精度。但是在實際運動平臺(機載或彈載)雷達系統中,通常面臨布陣空間有限的問題,無法充分利用MIMO雷達天線收發位置獲得最大的連續虛擬空間。所以通常考慮優化MIMO雷達的發射和接收陣元位置實現期望的和差波束方向圖[20-23]。

低副瓣陣列天線對于提升抗干擾、雜波性能等至關重要[22]。單脈沖估計中,需要對和差波束旁瓣同時抑制以保證測角精度。文獻[20]在陣元個數以及可排布陣列最大空間確定的條件下,對MIMO雷達發射陣列和接收陣列聯合稀疏優化設計,得到了較窄的主瓣以及較好的旁瓣水平,但僅涉及到和波束。文獻[24]提出了一種陣列綜合方法,用于設計單脈沖雷達可重構稀疏陣列的和差方向圖,與均勻間隔陣列相比,可以獲得更好的波束方向圖性能和更少的元件數量。當考慮對系統多種性能同時優化時,需要利用多目標進化算法(multi-objective evolutionary algorithm,MOEA),其中某一個目標求得的最佳方案是以其他目標性能下降為代價的[25-29]。文獻[28]針對全局最優陣列分布問題,提出了一種多目標粒子群優化搜索算法,在天線單元數量和旁瓣電平方面優于其他算法。文獻[29]利用多目標進化算法對相控陣雷達的多種性能進行了優化,使得干擾下的和差波束旁瓣等性能得到同時提升。

本文針對MIMO雷達天線的稀疏陣列優化問題,提出了基于Pareto秩排序的MOEA算法的稀疏陣列設計方法。該方法同時對MIMO雷達單脈沖測角時的和差波束進行優化,相當于在最優和波束和最優差波束之間進行折衷選擇,也就是說和波束性能的提高是以犧牲差波束性能為代價的,反之是同樣的。由MOEA得到的是最優陣列結構集,可以綜合考慮實際需求選擇合適的布陣方式。仿真實驗驗證了本文方法的有效性。

1 MIMO雷達信號模型

本文以運動平臺線陣MIMO雷達為信號模型,收發陣列共址。設MIMO雷達的發射和接收陣元分別為M個和N個,發射陣元間距為dT,接收陣元間距為dR,目標位于方位θ。在接收端,通過匹配濾波器分離接收到的目標回波信號,從而在MIMO雷達接收端形成等效發射波束[21-22]。對于單次發射信號,第n個接收陣元接收到的目標反射回波信號經第m個信號匹配濾波后的表達式為

xn,m(θ)=ρEme-j2π(m dT+n dR)sin θ/λ+nn,m

(1)

式中:ρ為發射系數；Em是每個發射信號的能量,這里假設Em=1,即每個陣元發射的信號能量都為1;nn,m為對應的高斯白噪聲輸出項。

將式(1)中匹配濾波得到的MIMO信號進行列向量化處理,可以得到MN維列向量,表示為

x=[x0,0,x1,0,…,xN-1,M-1]T

(2)

為了使得形成的波束指向特定的方位,使用加權向量ws對匹配濾波器組的輸出進行加權。根據空域波束形成理論以及匹配濾波理論,在θ0方向上ws的取值為

ws=wT?wR

(3)

式中:?表示Kronecker積;wT=[1,e-j2πdTsin θ0/λ,…,e-j2π(M-1)dTsin θ0/λ]T為發射波束形成的權向量;wR=[1,e-j2πdRsin θ0/λ,…,e-j2π(N-1)dRsin θ0/λ]T為接收波束形成的加權向量。

2 MIMO雷達稀疏陣列優化

2.1 MIMO雷達等效收發陣列

與相控陣雷達不同,MIMO雷達在接收端等效形成發射波束以得到聯合方向圖,再進行和差波束測角[20-22]。首先對式(2)進行分析,假設發射陣元多于接收陣元,各陣元之間間距相同,即M>N,d=dT=dR=λ/2;將各個接收陣元匹配濾波輸出的MN個值排成矩陣形式,可以表示為

(4)

通過觀察式(4)矩陣形式以及式(1)可以看出,式(4)中與副對角線平行的元素,除噪聲不同外,其信號部分完全相同,令fs=2πd/λ,式(4)中信號相位項可表示為

(5)

根據式(5)按副對角線進行合并,得到三角形陣列,如圖1所示。可以看出MIMO雷達等效陣列可以通過發射陣列與接收陣列卷積得到。若暫不考慮噪聲,則等效陣列相當于對長度為(M+N-1)的均勻線陣進行三角形加權得到,權向量為

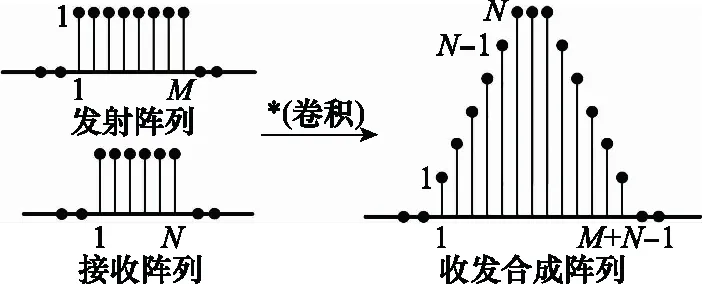
圖1 MIMO雷達等效合成陣列

此時,MIMO雷達等效收發波束的權矢量wnew可以表示為

wnew=diag(ws)·Q

(6)

2.2 MIMO雷達稀疏陣列多目標優化函數

對MIMO雷達陣列稀疏優化設計是通過優化其接收和發射陣元的位置實現的。目前MIMO雷達陣列主要的布陣方式有兩種:一種是緊湊布陣方式,發射陣列和接收陣列中相鄰陣元間距為半波長;另一種是稀疏布陣方式,發射陣列和接收陣列均為相鄰陣元間隔d=λ/2的稀疏陣列。其中,規則稀疏布陣和發射陣元間距為接收陣列的孔徑,接收陣列按照半波長布置,可以獲得最大的虛擬連續孔徑。但在機載或彈載平臺應用中即使在陣元數不多的情況下也難以實現規則稀疏布陣,此時MIMO雷達陣列通常采用不規則稀疏布陣方式[30-31]。

假設MIMO雷達共有M0個發射位置和N0個接收位置,分別布置M個發射陣元和N個接收陣元。PT是發射陣元位置序號,PR是接收陣元位置序號。PT、PR可以分別表示為PT=[PT,0,PT,1,…,PT,M-1],PR=[PR,0,PR,1,…,PR,N-1],其中PT,0=PR,0=0,PT,M-1=M0,PT,N-1=N0。QT是發射陣元位置構成的M0×1維向量,與PT陣元序號對應的元素為1,其余為0,同時QT中的第一個元素也應該設為1。類似地,QR是接收陣元位置構成的N0×1維向量。則有:

Q0=QT*QR

(7)

式中:*表示卷積。

由式(6)可得MIMO雷達稀疏陣列的等效收發和差波束權矢量為

wΣ=diag(ws)·Q0

(8)

wΔ=diag(diag(ws)·U)·Q0

(9)

式中:U=[-1,-1,…,-1,1,1,…,1]T。

由上述式(8)和式(9),令K=M0+N0,對于不規則稀疏陣列結構的MIMO雷達和差波束可以表示為

(10)

(11)

式中:u=sinθ-sinθ0；(·)*表示復數共軛。

根據參考文獻[20],MIMO雷達稀疏陣列設計的和差波束的旁瓣峰值目標函數可以表示為

(12)

(13)

式中:RΣ、RΔ分別為和差波束形成加權系數wΣ,m、wΔ,n之和;uend設置為1,uΣstar、uΔstar的取值可以將主瓣區別于旁瓣。

從式(12)和式(13)可以看出,fΣ、fΔ都是由陣元位置PT和PR決定的。因而,待優化的問題以多目標優化形式可以描述如下:

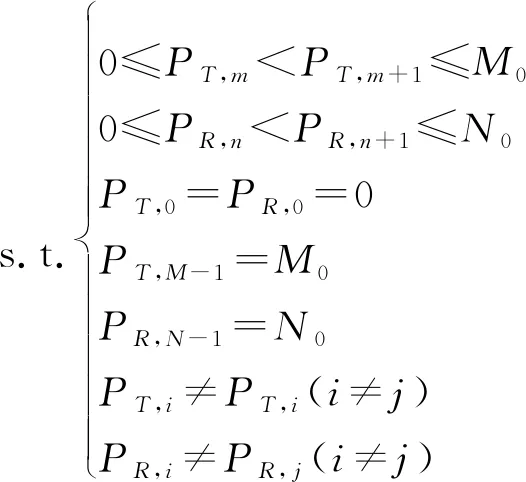
(14)

利用MOEA對式(14)優化所得到的最優解并不是唯一的,而是一個解集合,稱為Pareto最優解。所有Pareto最優解對應的目標函數值形成的最優區域稱為Pareto前沿,MOEA的優化就是不斷逼近Pareto前沿的過程。

2.3 MIMO雷達稀疏陣列優化流程

采用既帶有精英保留策略又可以快速非支配排序遺傳算法(non-dominated sorting genetic algorithm, NSGA)-Ⅱ作為本文MIMO雷達陣列結構優化的MOEA。NSGA-Ⅱ算法是在NSGA的基礎上改進而來的,具有運行速度快、解集收斂性好的優點。算法流程圖如圖2所示。

圖2 NSGA-Ⅱ算法流程圖

下面對NSGA-Ⅱ算法陣列優化過程中的主要步驟進行說明:

(1) 產生初始種群G0:在1～(M0-1)之間隨機生成(M-2)個從小到大的整數形成向量A,則可得發射陣元位置向量PT=[0,A,M0],同理可得接收陣元位置向量PR。將發射和接收陣元位置矢量結合,種群中個體可以表示為P=[PT,PR]。隨機生成若干組向量P得到初始種群G0。

(2) 產生新種群:計算種群個體的序值和擁擠距離。對于兩個個體,當序值不同時,選擇序值小的個體;若序值相同,選擇擁擠距離大的個體。然后將選中的個體通過交叉和變異操作產生子代種群H0,并修正子代H0中的個體使其滿足約束條件。

(3) 修剪種群:將Gt和Ht并入到Rt中(初始時t=0),對Rt進行快速非支配解排序,構造其所有不同等級的非支配解集F1,F2,…。按照需要計算Fi中所有個體的擁擠距離,并根據擁擠比較運算符構造Gt+1,直至Gt+1規模等于G0。

3 仿真結果

仿真參數設置如下:設有發射陣元M=16,按d的整數倍間距放置在0～32λ范圍內的柵格上;接收陣元N=8,按d的整數倍間距放置在0～16λ范圍內的柵格上,其中d=λ/2。設θ0=0,和波束uΣstar設置為0.03,差波束uΔstar設置為0.07。在進化參數中,種群大小為200,迭代代數為100,交叉概率為0.9,變異概率為0.1。原始陣列結構隨機選取。

3.1 和波束最優旁瓣電平

圖3(a)給出了本文方法稀疏陣列結構優化后和波束的收發聯合方向圖,為了方便比較,同時給出文獻[20]優化后和原始陣列結構對應的方向圖。可以看出,本文方法與文獻[20]方法優化后的旁瓣峰值水平相當,都可以將旁瓣峰值控制在-20 dB以下,且保持較窄的主瓣寬度,原始陣列結構旁瓣峰值為-11.7 dB,即優化后改善了約8.3 dB。和波束優化對應的發陣陣元位置為[0，4，6，8，14，19，22，23，27，35，40，42，43，44，51，64]×d;接收陣元位置為[0,14,15,20,23,25,26,32]×d。與文獻[20]的最優布陣結果相比,發射陣列與接收陣列布置方式存在差異,這是因為:一方面滿足約束條件的布陣方式較多,可能會出現不同布陣方式對應相同結果的情況;另一方面使用的優化算法為準最優算法,每次仿真結果存在一些偏差。此外,圖3(c)本文方法優化后的陣列在波束指向-40°、0°、10°、30°的方向圖,可以看出經優化后的陣列在其他方向掃描時仍能保持良好的旁瓣性能。

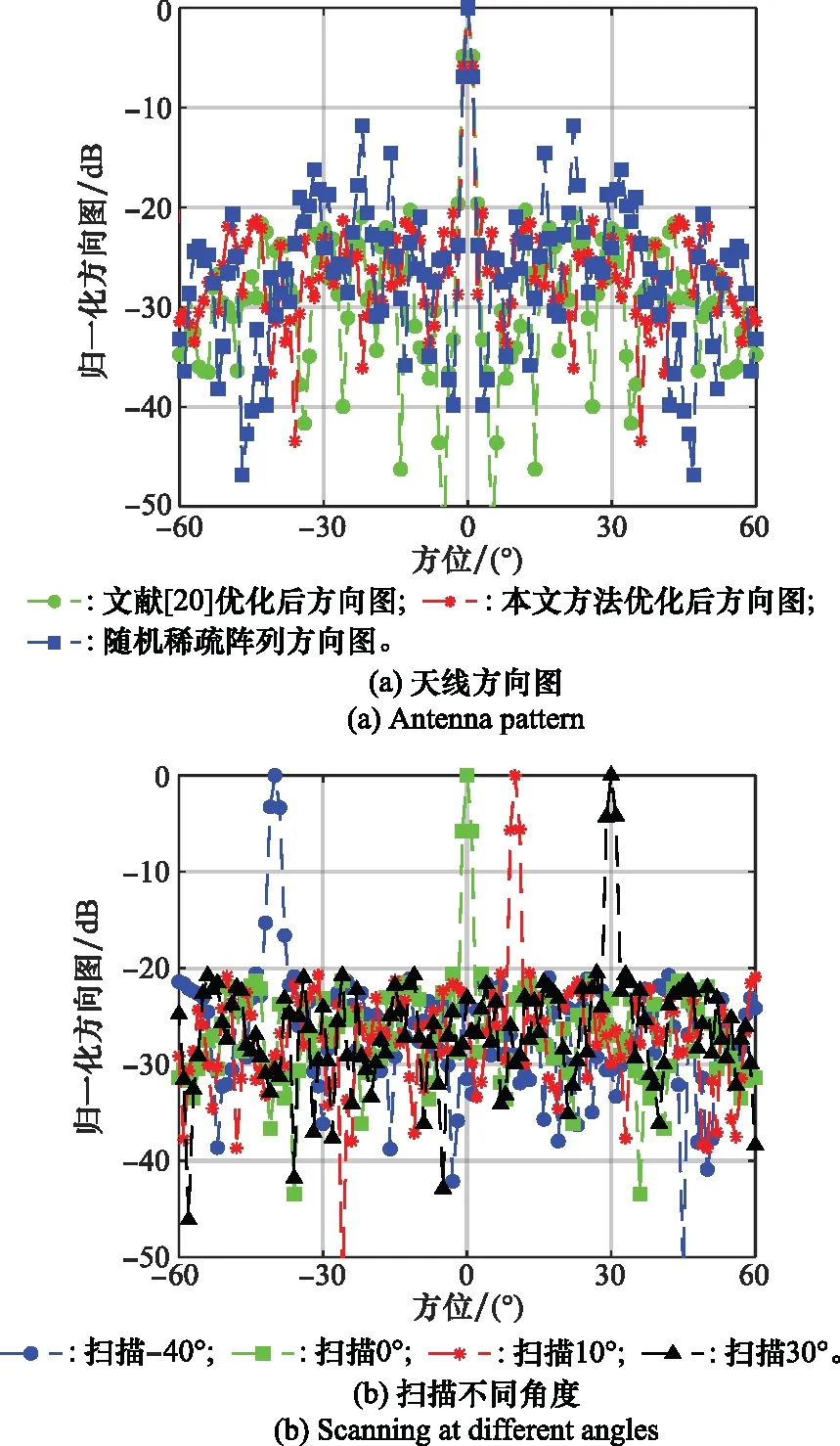
圖3 和波束優化結果

3.2 差波束最優旁瓣電平

圖4(a)給出了本文方法稀疏陣列結構優化后差波束的收發聯合方向圖,同時給出了由文獻[20]和波束最優布陣結果生成的差波束和原始陣列生成的差波束作為對比。可以看出,本文方法對差波束優化后,方向圖旁瓣峰值電平得到了改善,優化后和原始陣列的旁瓣電平峰值分別為-16.7 dB和-9.6 dB,即旁瓣峰值改善了7.1 dB,相比于文獻[20]給出的布陣方式對應的旁瓣電平峰值-15.4 dB改善了1.3 dB。差波束優化對應的發陣陣元位置為[0,4,7,8,12,16,20,24,28,38,39,43,47,48,51,64]×d;接收陣元位置為[0,14,16,17,19,25,26,32]×d。圖4(b)給出了優化后的陣列在其他方向掃描時的方向圖,實際中單脈沖測角時只考慮差波束在波束中心指向0°附近時的性能,這里僅是為了說明經優化后的陣列在其他方向掃描時仍能保持良好的旁瓣性能。

圖4 差波束優化結果

3.3 Pareto最優解集

為了驗證目標優化性能,圖5給出了優化后的和波束、差波束旁瓣峰值電平對應的Pareto最優解。可見最優解分布并不十分均勻,這是由于約束條件的限制,使得部分非法解被剔除的結果。但是從圖5中仍可以看到，其具有收斂趨勢。同時可以看出,基于Pareto最優解的稀疏布陣設計提供了多種最優布陣方案,可以根據實際需求靈活選擇,比如在檢測階段選擇和波束最優的稀疏陣列結構即可,可以得到較窄的主瓣以及較好的旁瓣水平,提高對低速目標的探測能力等;在對目標單脈沖測角定位階段需要同時考慮和差波束旁瓣水平,這時可以選擇Pareto前沿中間的目標函數值所對應的陣列結構,相當于對最優性能折衷,獲得盡可能好的測角性能。

圖5 Pareto最優解

4 結 論

本文首先建立了一般MIMO雷達的信號模型,并推導了其等效合成陣列形成過程,然后給出了稀疏陣列結構下MIMO雷達的和差波束,采用MOEA對MIMO雷達的和波束及差波束同時優化,得到了一個Pareto最優陣列結構解集合,和差波束的旁瓣抑制能力得到了提高。在后續的實際應用中可以根據需求,在得到的最優陣列結構解集合中進行選擇,以最終確定所需要的陣列結構。