基于雙層全局靈敏度分析的車輛系統響應特性研究及驗證

王振峰 嚴格 楊建森 李洪亮 田陽

（1.中汽研（天津）汽車工程研究院有限公司，天津 300300；2.柳州五菱汽車工業有限公司，柳州 545000；3.燕山大學，秦皇島 066004）

主題詞：車輛動力學 靈敏度分析 響應特性 耦合車輛模型

1 前言

車輛動力學模型是自動駕駛算法、車輛動力學控制算法、底盤/懸架控制算法的核心基礎，其關鍵參數對深入分析底盤性能優劣與車輛系統響應特性有較大影響，研究模型關鍵參數對車輛系統的響應特性不僅有利于縮短車輛新技術的開發時間，且可有效降低開發成本[1-2]。在當下日益復雜的交通環境和駕駛場景（如轉彎制動、障礙物緊急避障與路徑跟蹤等[3-5]）輸入工況下，采用非耦合或單車模型的車輛動力學控制很難實現令人滿意的底盤操縱穩定性與乘坐舒適性。與此同時，如何在控制器開發中設計快速高效的基于耦合車輛模型的集成控制方法成為該領域的研究熱點與難點[6-7]。

車輛核心參數對車輛系統瞬態與穩態動態響應有很大影響，深入研究車輛系統關鍵參數與系統響應之間的對應關系，將有助于更好地理解車輛動態響應及其底盤集成控制。靈敏度分析（Sensitivity Analysis，SA）被認為是基于量化參數對系統輸出響應特性物理描述的有效方法[8-9]。

本文基于雙層全局靈敏度分析（Global Sensitivity Analysis，GSA）方法研究車輛系統參數與響應之間的關系，提出一種新的雙層全局靈敏度分析方法，以減少蒙特卡羅技術帶來的高計算量。以整車橫向-縱向耦合的非線性車輛模型作為分析對象，并在不同轉向盤轉角與路面激勵復合輸入工況下對所提出的GSA方法進行驗證。

2 整車垂向與橫向動力學建模

2.1 車輛系統運動學分析

為了獲得整車垂向與橫向動力學函數關系，建立包含車輛的側傾運動、車身俯仰運動、車身垂向運動、橫向運動、橫擺運動以及4 個輪胎的垂直運動的整車9自由度模型，如圖1 所示。其中：a、b分別為車輛質心與前、后軸的距離；δfl、δfr分別為車輛左、右前輪轉角；αf、αr分別為前、后輪側偏角；lt為輪距；x、y分別為車輛縱、橫向運動距離；vx、vy分別為車輛質心縱、橫向速度；ci、ksi分別為各輪懸架阻尼、垂向剛度；kti為各輪輪胎剛度；zb、zwi分別為車輛質心的垂向位移、各輪非簧載質量的垂向位移；M、ms、mwi分別為車輛總質量、簧載質量、各輪非簧載質量；zri為各輪路面激勵位移；hroll為車輛側傾中心與質心間的距離；Ix、Iy、Iz分別為車輛側傾、俯仰、橫擺轉動慣量；Cf、Cr分別為車輛前、后輪側偏剛度；φ、θ分別為車輛簧載質量側傾角、俯仰角；ω為車輛簧載質量橫擺角速度；ay為車輛側向加速度；Fy1、Fy2、Fy3、Fy4分別為車輛左前、右前、左后、右后輪輪胎側向力。

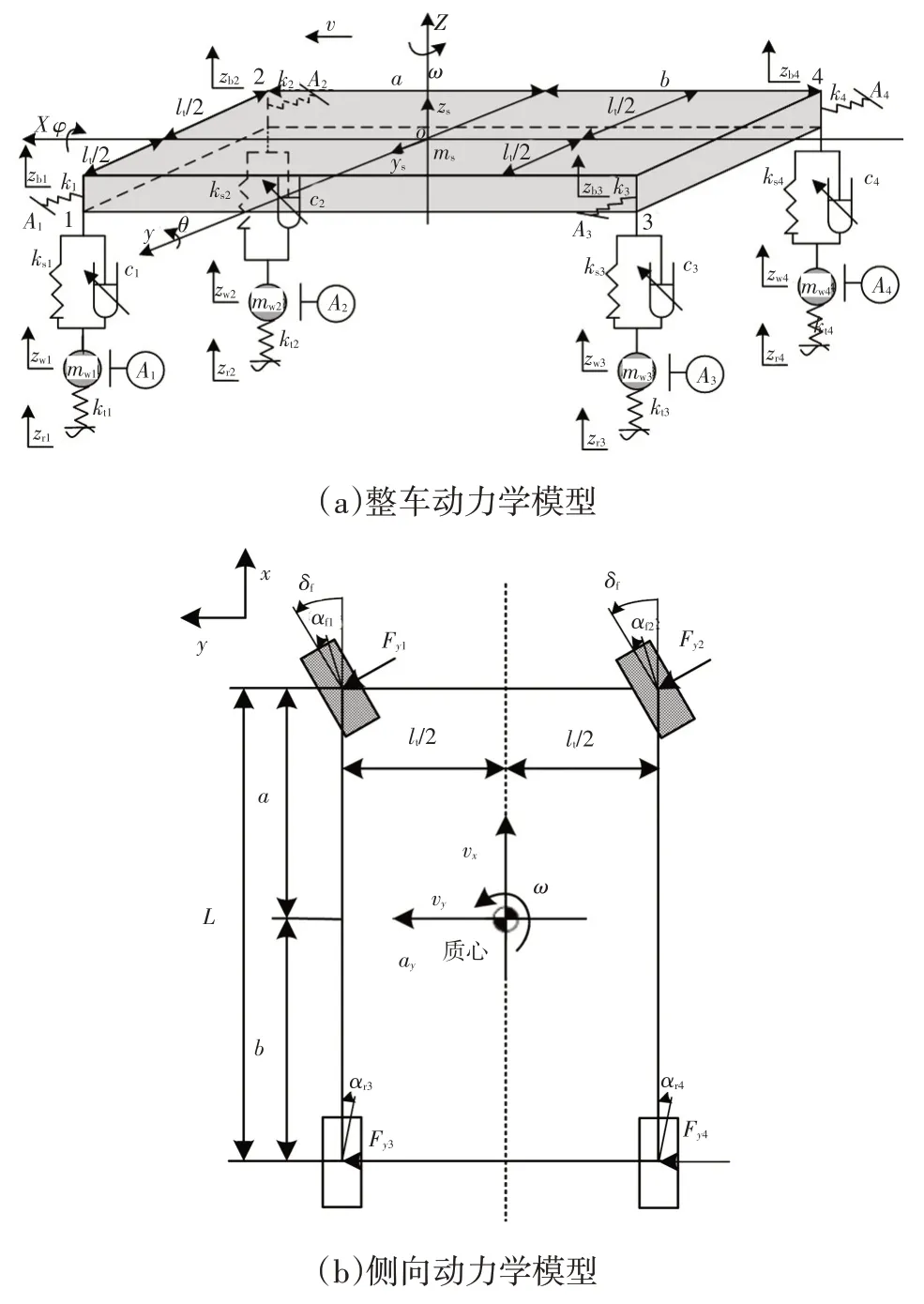
圖1 9自由度整車模型

在車輛參考坐標系Sv中，簧載質量質心位置為：

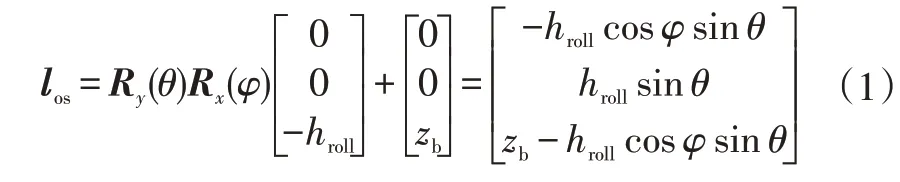
且

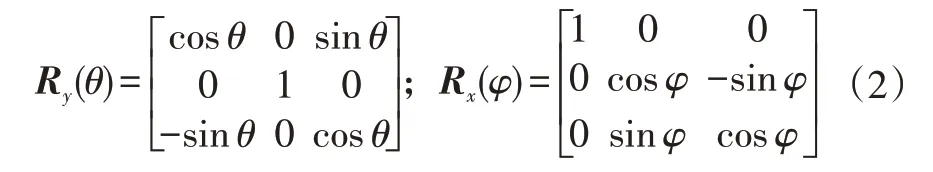
故地面坐標系G與車輛坐標系v之間的關系為：

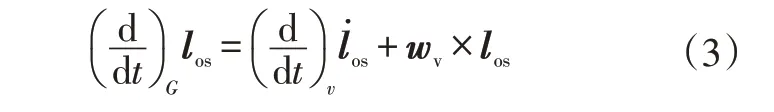
式中，wv=[0 0ω]T為旋轉運動矢量；Rx、Ry分別為繞X軸、Y軸的極坐標；為車輛質心位置的偏導。

車輛相對地面固定坐標系SG的質心速度vs可以用相對車輛坐標系的車輛速度vv與los表示：

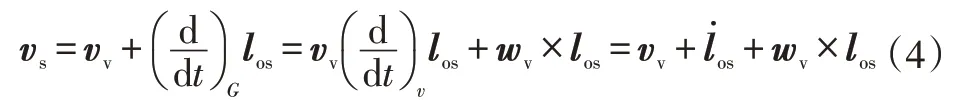
與此同時，相關的簧載質量加速度、非簧載質心相對位置及其相對的旋轉運動可分別表示為：

a.車輛簧載質量加速度as相對坐標系SG的計算公式為：

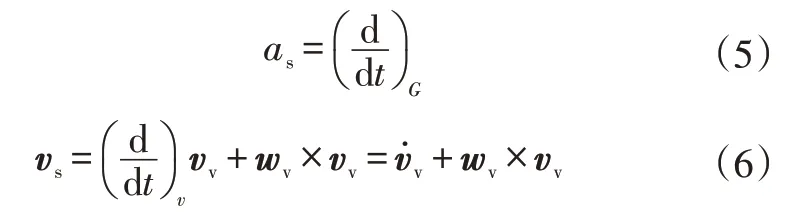
b.車輛非簧載質量質心的轉移。利用車輛簧載質量質心轉移方法，非簧載質量質心相對坐標系Sv的轉移可表示為：

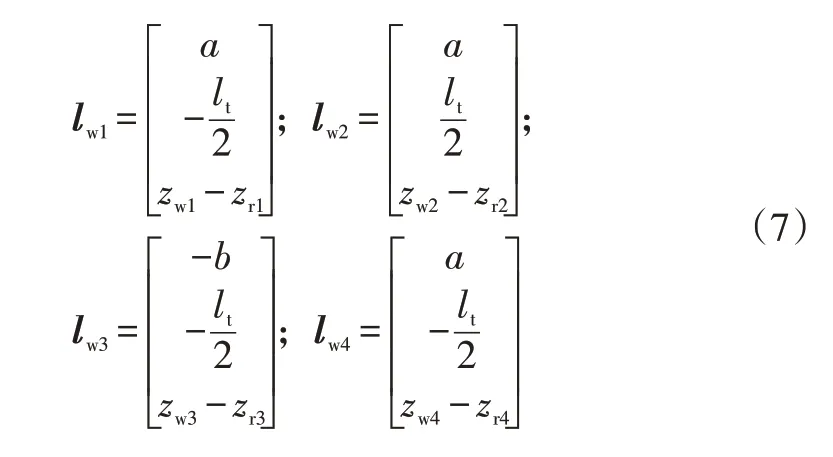
式中，lwi為非簧載質量質心轉移矩陣。

c.車輛簧載與非簧載質量質心的旋轉運動。簧載質量的旋轉角動量Ds可表示為：

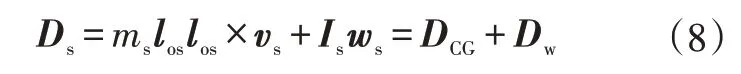
式中，DCG為質心角動量；Dw為非簧載質量角動量。

同時，非簧載質量角動量Dw可表示為：

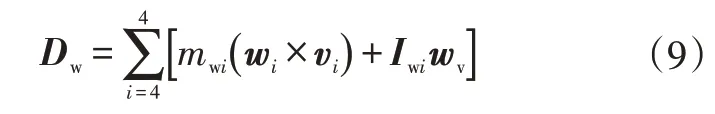
式中，wi、vi分別為旋轉與直線運動速度矢量。

2.2 輪胎建模

Pacejka[10]提出的“魔術公式”可以很好地描述輪胎橫向非線性特性：

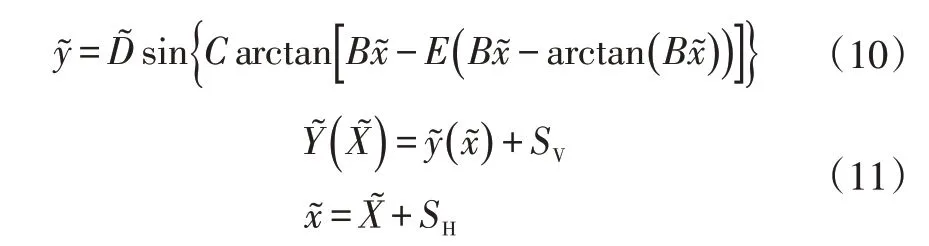
式中，高高高高為輸入狀態，主要指滑移率或側偏角；高高高高為輸出量，主要指橫向力、縱向力或回正力矩；影響因子B、C、、E分別為試驗擬合曲線的斜率、試驗曲線的形狀、峰值、曲率，可從試驗數據中獲取；SH、SV分別為輸入與輸出狀態的補償量。

2.3 整車模型

由牛頓第二定律以及圖1所示的整車9自由度動力學模型可知，針對整車的不同運動，有：

a.車輛簧載質量垂向運動方程為：

式中，Fsi為第i個簧載質量懸架作用力；為簧載質量總的垂向加速度。

Fsi可表示為：

同時：

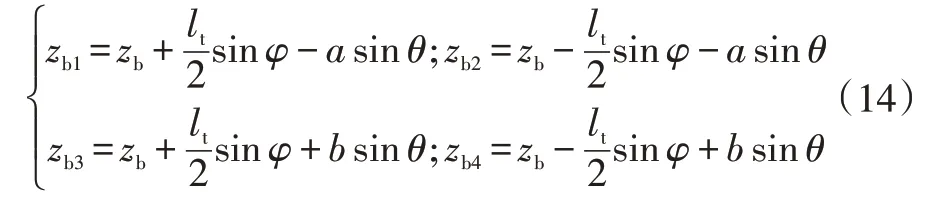
b.車輛非簧載質量垂向運動方程為：

式中，Fwi為第i個非簧載懸架作用力；為非簧載質量總的垂向加速度。

Fwi可表示為：

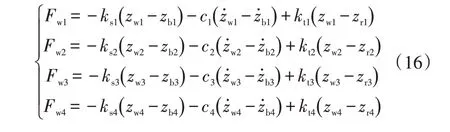
同時，整車左前輪、左后輪、右前輪、右后輪對應的垂向輪胎力可分別表示為：

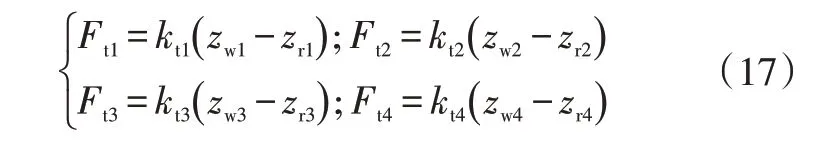
c.車輛俯仰運動方程為：

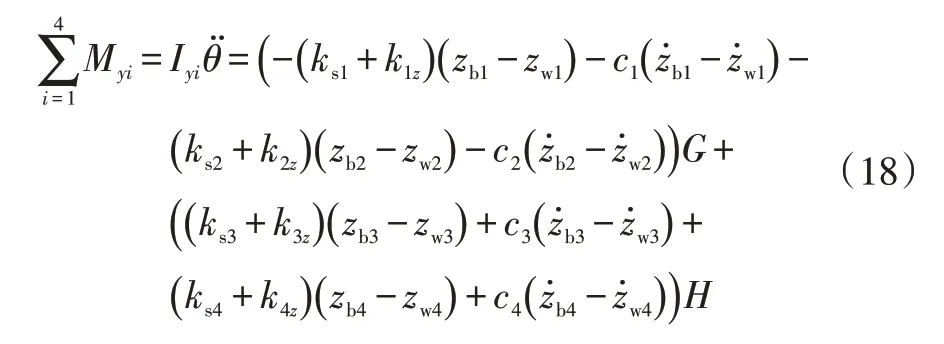
式中，Myi、Iyi分別為車輛不同i位置對應的俯仰力矩和俯仰轉動慣量；kiz為車身與懸架系統不同接觸位置彈簧剛度的垂向分量；G、H為關于俯仰運動的函數。

d.車輛側傾運動方程為：

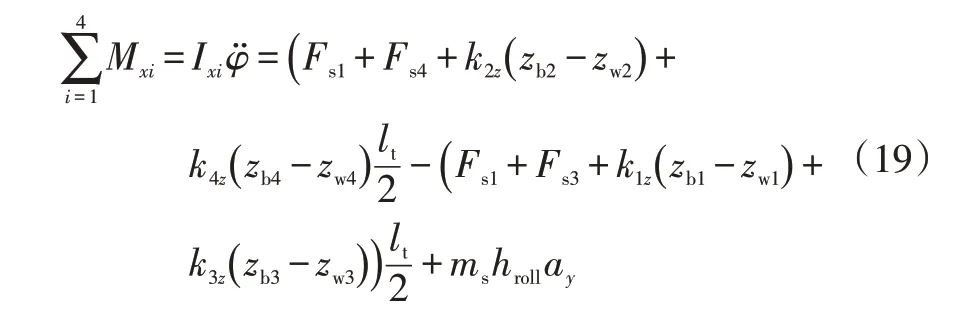
式中，Mxi、Ixi分別為車輛不同位置i的側傾力矩和側傾轉動慣量；kiz為車身與懸架系統不同接觸位置i的彈簧剛度的垂向分量。

e.車輛橫向運動方程為：

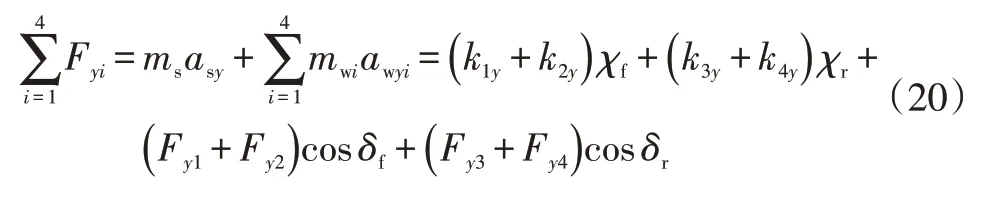
式中，Fyi為車輛轉向離心力所產生的車輛不同位置橫向力；kiy為車身與懸架系統不同接觸位置彈簧剛度的橫向分量；χf、χr分別為俯仰、側傾相關的函數，是車身對應位移變量；asy、awyi分別為簧載質量橫向加速度、非簧載質量橫向加速度；δf、δr分別為前、后輪的轉向角。

f.車輛橫擺運動方程為：

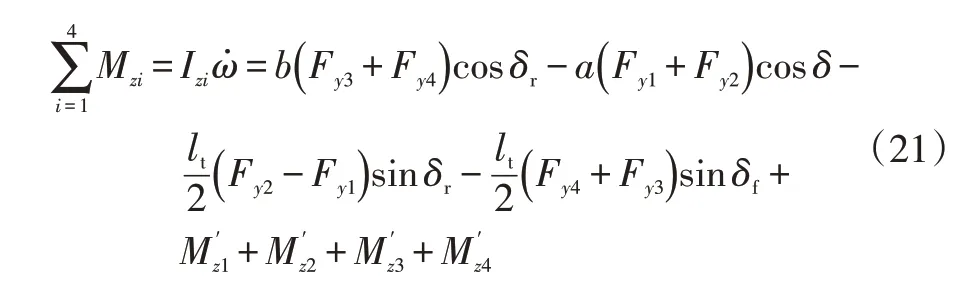
式中，Mzi、Izi分別為車輛不同位置橫擺力矩和橫擺轉動慣量；為車身與懸架系統不同接觸位置的橫向力矩。

3 系統全局靈敏度篩選理論

針對復雜多變量系統輸入工況，由于無法較好地獲取系統關鍵參數以及常規參數之間的內在耦合關系，導致無法對系統響應特性進行定量研究。為有效解決上述問題，本文利用GSA 方法中莫里斯（Morris）篩選方法的首要影響（Elementary Effects，EE）與基于方差（Variance-based，VA）理論，全面定量分析參數對車輛系統響應狀態的影響，對應的整體流程如圖2所示。

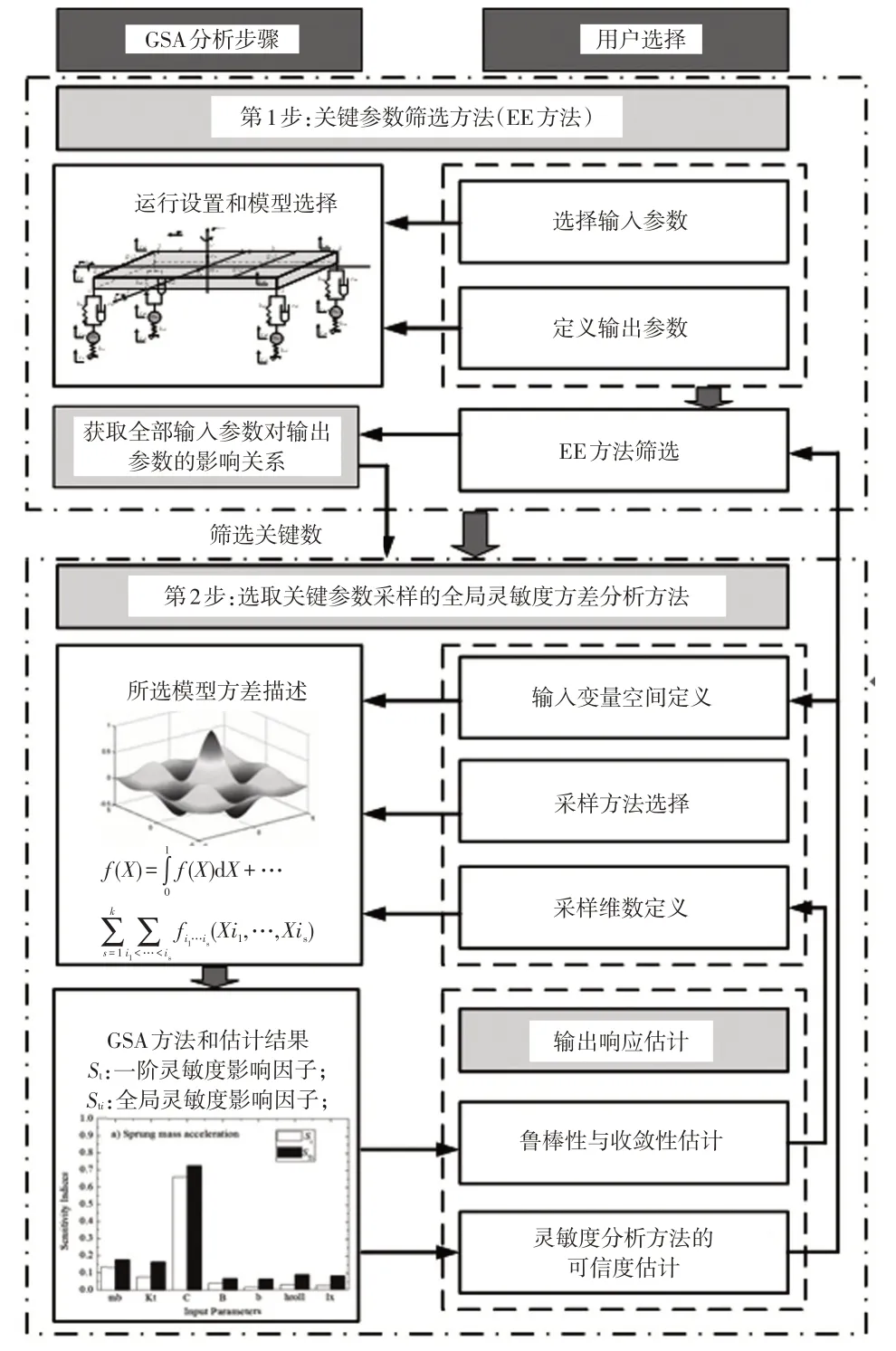
圖2 雙層GSA方法整體分析流程

3.1 Morris參數篩選方法

假設已知系統模型具有n個獨立輸入xi(i=1,2,…,n)，此系統輸入在n維空間中決定著p個系統輸出，對于已知的系統輸出參數X，利用EE方法可得第i個輸入元素對已知系統模型的影響Eii：

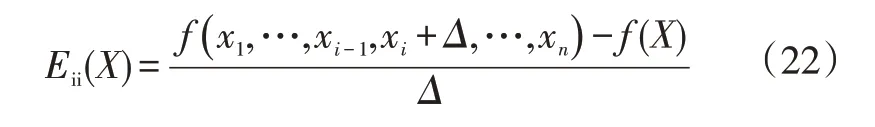
式中，Δ為預定義數值且取值范圍為{1/(p-1),2/(p-2),…,(i-1)/(p-i)}；由于X=(x1,…,xi-1,xi,…,xn)是輸入參數空間的隨機采樣，同理傳遞點(x1,…,xi-1,xi+Δ,…,xn)也是輸入參數空間。

此處，EE方法提供2種測量敏感性數據分析方式：估計輸入參數對于系統輸出的整體均值μ；估計輸入參數之間非線性與相互作用的最高階方差σ。為了準確估計μ與σ，此處對不同輸入參數x進行參數區域X中的隨機采樣，以保證采樣區域的完整性。其中，μ代表EE方法的分布均值，其數值與相關度成正比；σ代表輸入參數的非線性對輸出響應的影響，其數值與非線性成正比。考慮到部分函數是非單調函數，其求解的μ存在正負相消的情況，為了改進此工況，本文采用改進的μ*(|Eii|)描述以上問題：

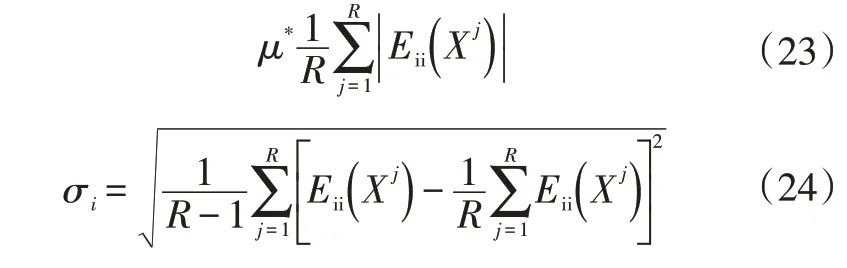
利用上述理論，參考CarSim 動力學軟件提供的不同等級乘用車參數，對車輛懸架系統關鍵參數進行整理，如表1所示。

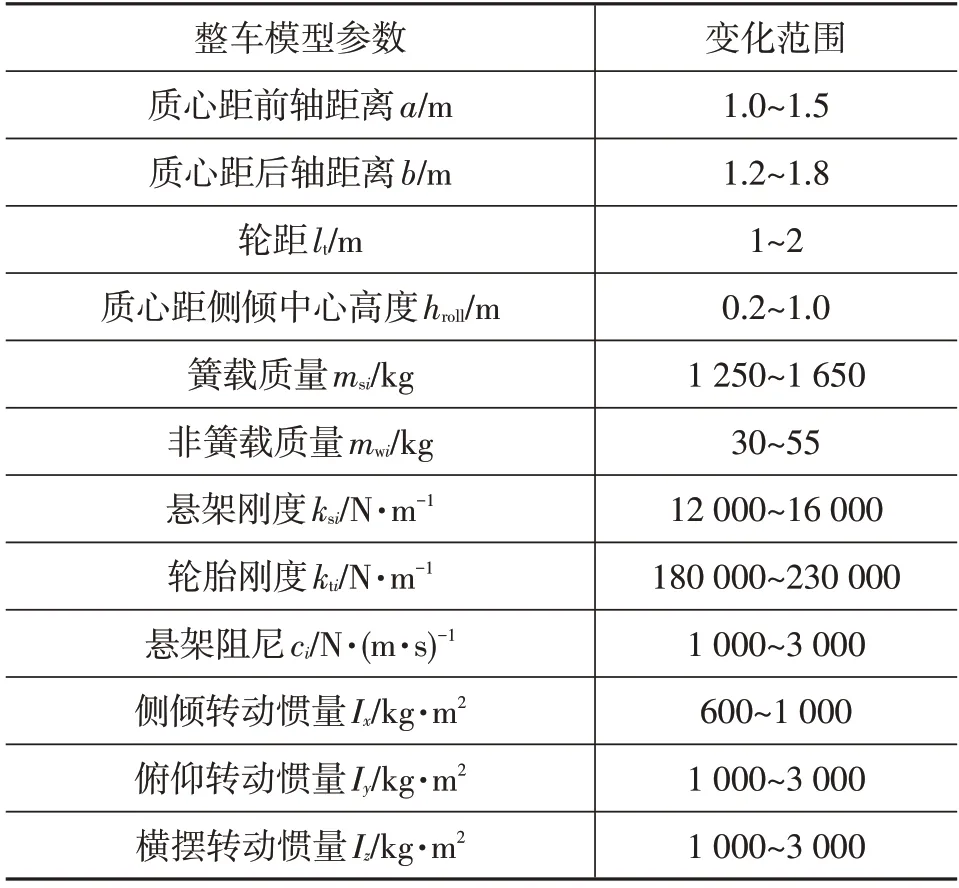
表1 整車系統參數選取范圍

3.2 Morris篩選方法驗證

利用CarSim 動力學軟件中所提供的B 級車型（Hatchback），在80 km/h 車速、不同轉向盤轉角且不同路面激勵工況下進行車輛系統輸出參數對其垂向與橫向響應影響的靈敏度分析驗證，分別可得到不同轉向盤轉角以及ISO-A/C 級路面激勵工況下，Hatchback 車型對應的系統輸入參數與系統響應之間的靈敏度對應關系，如圖3所示。

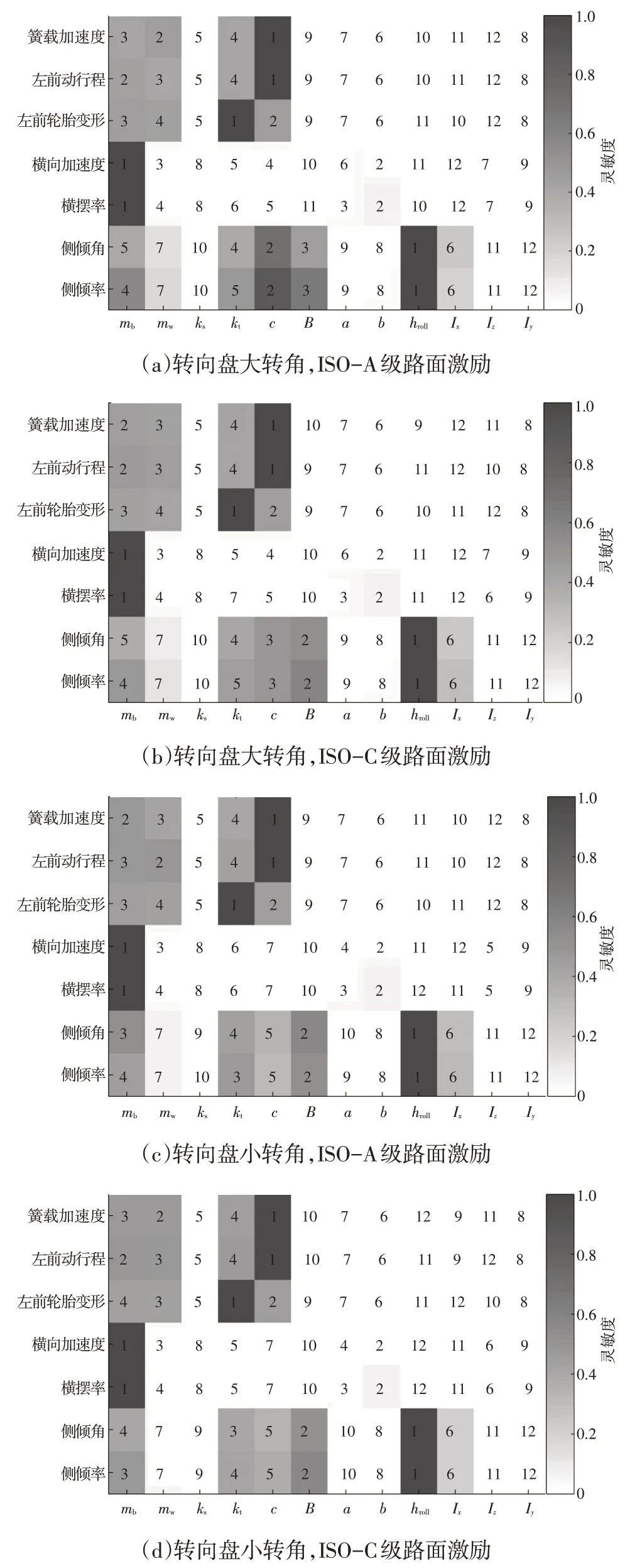
圖3 不同工況下B級車型參數對系統垂向與橫向響應靈敏度

由圖3a、圖3b 可知，轉向盤大轉角正弦輸入ISOA/C 級路面激勵工況下：車輛懸架系統的垂向響應（車輛簧載加速度、左前動行程與輪胎變形）主要受懸架阻尼、簧載質量、非簧載質量、輪胎剛度以及懸架剛度影響；橫向響應（橫向加速度與橫擺角速度）主要受到簧載質量、質心與車輛前、后軸之間的距離以及懸架阻尼的影響，且影響趨勢依次遞減；側傾響應（側傾角與側傾角速度）主要受到質心與側傾中心間的側傾高度、懸架阻尼、輪距、簧載質量以及側傾轉動慣量的影響。ISO-C級路面激勵工況與ISO-A級路面激勵工況相比，影響車輛垂向響應、橫向響應以及側傾響應的主要系統參數及影響程度類似。由此可知，Hatchback 車型在轉向盤大轉角輸入且不同路面激勵工況下，系統響應與系統輸入參數之間靈敏度權重關系相對固定。

由圖3c、圖3d 可知，轉向盤小轉角輸入工況下，Hatchback 車型在ISO-A/C 級路面激勵工況下，車輛懸架系統的垂向響應也主要受懸架阻尼、簧載質量、非簧載質量、輪胎剛度以及懸架剛度影響，且對應參數影響權重也相近。由此可知，B級車型（Hatchback）在轉向盤小轉角不同路面激勵工況下，路面因素對車輛系統響應影響較弱，且車輛垂向與橫向響應主要受簧載質量影響。由于在此激勵工況下，懸架阻尼與輪胎剛度主要影響車輛垂向響應，但對橫向響應影響較弱；質心與車輛前、后車軸距離主要影響車輛橫向響應，但對垂向響應影響較弱；車輛側傾響應主要受簧載質量質心位置、懸架阻尼、輪距、簧載質量以及側傾轉動慣量影響，其他整車參數影響相對較弱。

4 系統全局靈敏度方差分析

4.1 Sobol敏感測試方法

基于協方差分析理論，Sobol 方法可以有效計算輸入參數及其之間的耦合關系對系統輸出的靈敏度[11]。首先，利用協方差方法計算系統分解方差V(i1…iX)：

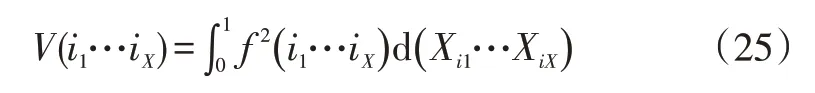
且全局方差V為：

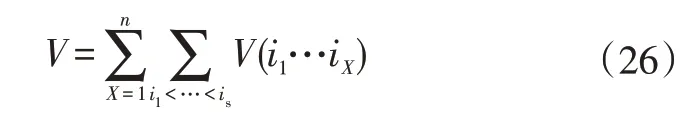
同時，全局靈敏度索引方差因子S(i1…iX)可表示為[12]：

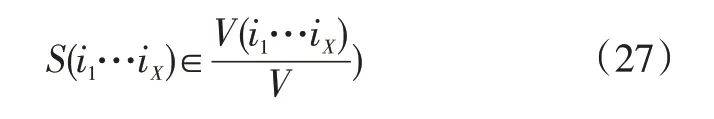
利用式（27）可知全局靈敏度索引因子為非負值，且：

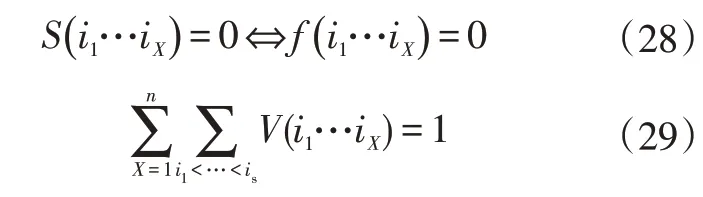
其中，S(i1…iX)代表一系列變量i1,…,ix的靈敏度測量，與全局方差一一對應，即S1主要受參數X1影響，S12主要受X1與X2參數相互關系因素影響。

4.2 蒙特卡羅方法

在應用Sobol方法進行全局靈敏度分析時，均需使用蒙特卡羅方法求解對應系統參數的方差。具體可表示：

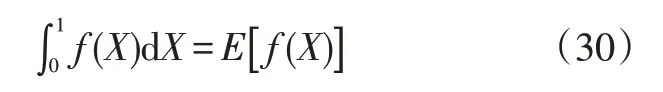
式中，E[f(X)]為數學期望，且近似為：

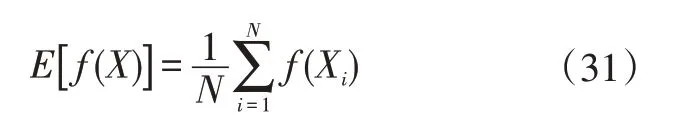
式中，{Xi}為空間In中長度為N的隨機序列，且當N→∞時式（30）和式（31）近似相等，且對應參數之間相互關系如表2、表3所示。其中，Sα為所有參數方差S(i1…iX)，為所有輸入參數對系統輸出的靈敏度索引因子，I為單位矩陣。

表2 α與β子集靈敏度索引因子關鍵參數總結

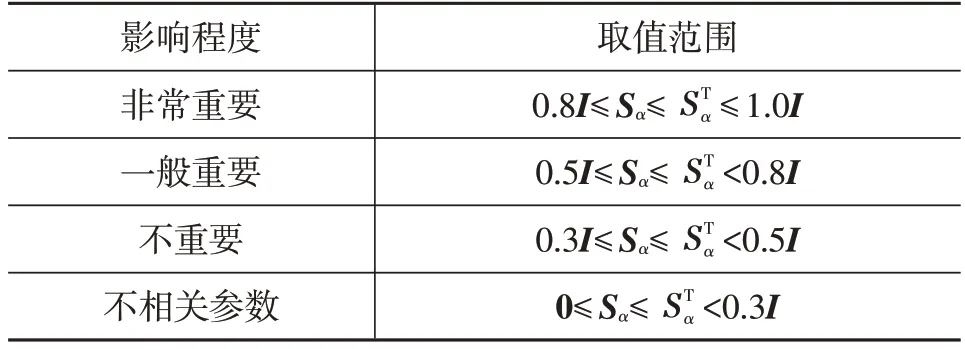
表3 基于全局靈敏度索引因子的輸入參數相關性

首先，在空間In中選取2 個隨機獨立的一致點，即π1=[α1;β1]與π2=[α2;β2]；利用模型f(X)對這2 個點進行估計，得到f(π1)與f(α1;β1)。假設模型f(X)平方可積，對于獨立采樣點N（N→∞），有：

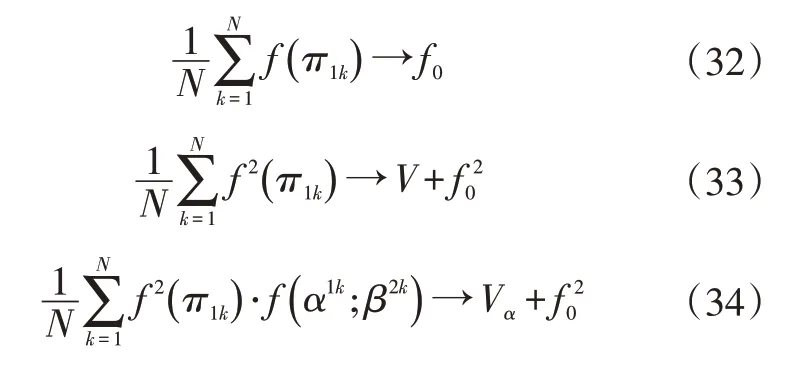
利用式（32）～式（34）可對一階靈敏度索引因子Vα進行變換：

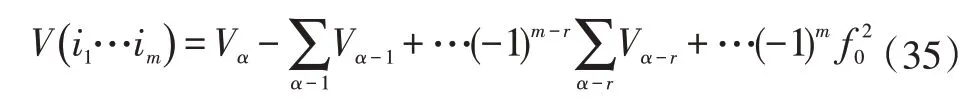
式（35）說明了V(i1…im)關于參數α在(m-r)維隨機序列中的方差總和，且π1k為第k點的隨機獨立一致點。

同時，在置信度50%工況下的Vα估計關聯誤差可表示為：

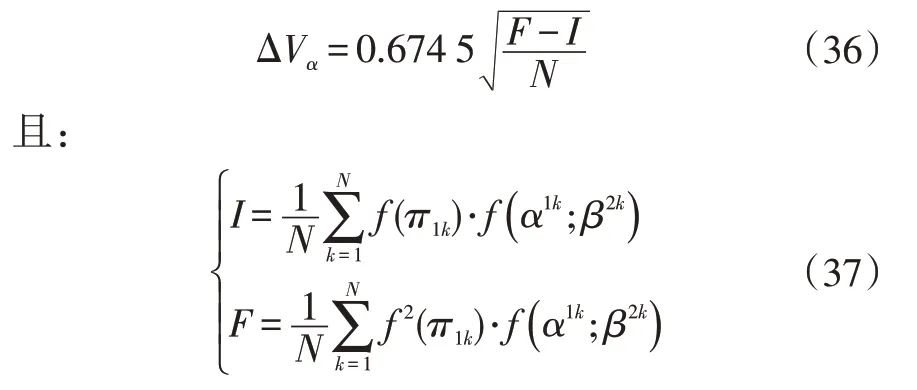
采用以上方法可以有效避免蒙特卡羅方法在隨機取點中的堆棧以及取空等問題，且為減少取樣數量N，對于采樣k插入2n維擬隨機點，并將其平分為2 個n維的與，對其進行描述計算。

4.3 全局靈敏度方差分析方法仿真分析

利用以上理論，可得此工況下對應的簧載質量、輪胎剛度、懸架阻尼、輪距、質心與后軸的距離、側傾中心與質心的距離以及側傾轉動慣量對應車輛垂向以及橫向響應的一階靈敏度影響因子，以及全局靈敏度影響因子，如圖4所示。

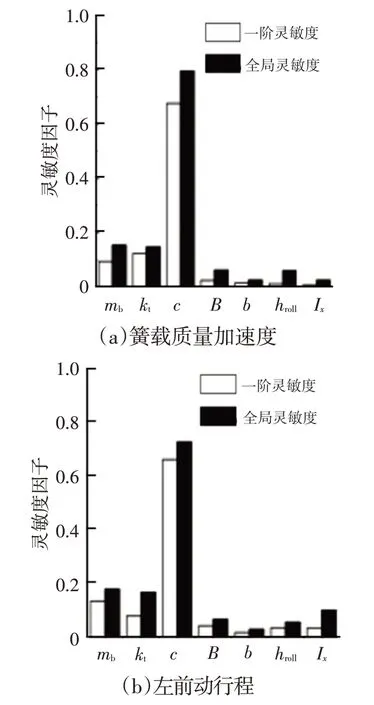
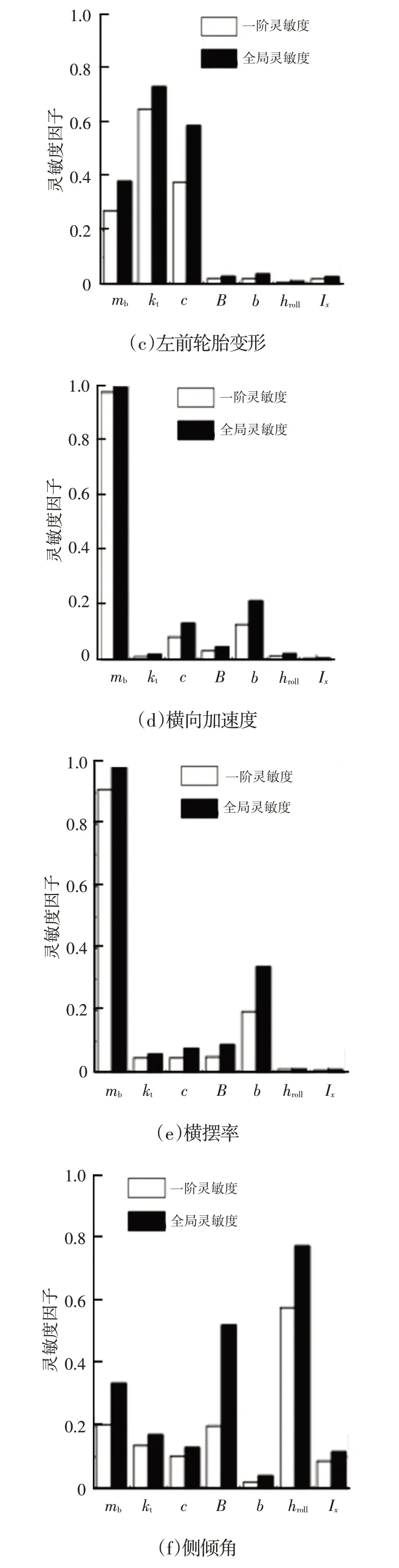
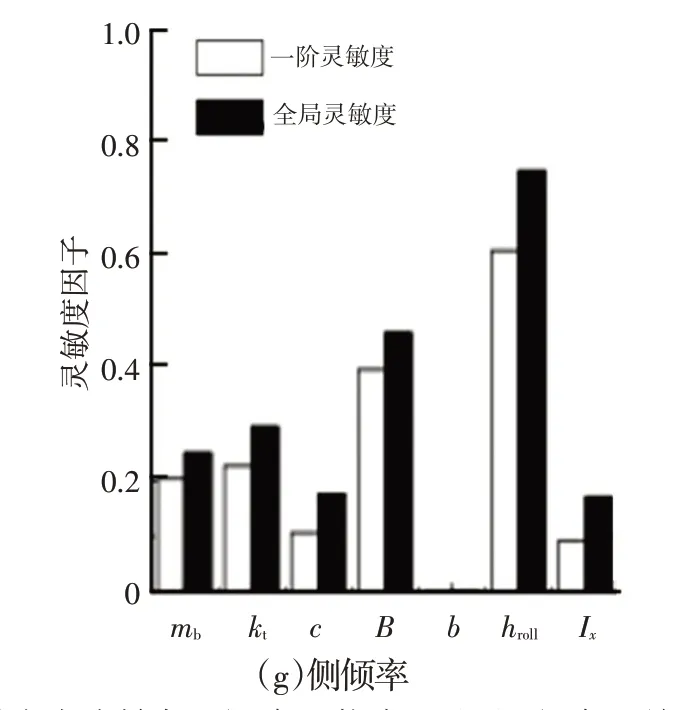
圖4 轉向盤小轉角A級路面激勵工況下B級車型關鍵系統參數對垂向與橫向響應全局靈敏度影因子

由圖4可知：此工況下車輛懸架垂向響應主要受懸架阻尼、輪胎剛度、簧載質量以及懸架剛度參數影響；橫向響應主要受到簧載質量、質心與車輛前、后軸之間的距離的影響，且影響程度依次遞減；側傾響應主要受簧載質量質心位置、懸架阻尼、輪距、側傾轉動慣量以及簧載質量影響，且影響程度依次遞減。

參考轉向盤小轉角A級路面激勵工況，可得此工況下系統輸出參數對應車輛垂向與橫向響應的一階靈敏度影響因子以及全局靈敏度影響因子，如圖5所示。

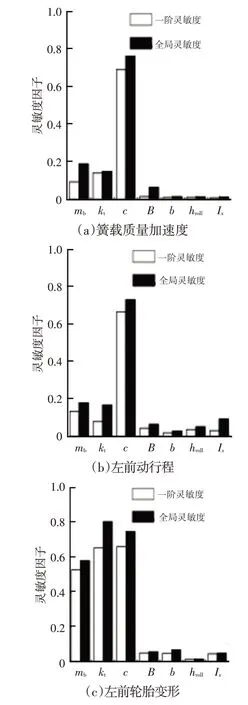
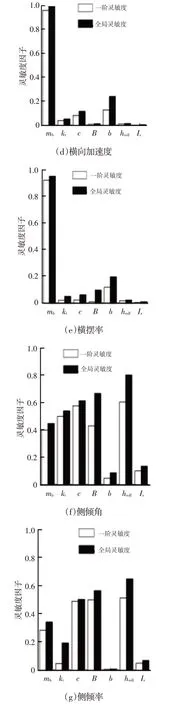
圖5 轉向盤大轉角C級路面激勵工況下B級車型關鍵系統參數對垂向與橫向響應全局靈敏度影因子

由圖5可知：此工況下車輛懸架垂向響應受懸架阻尼、簧載質量、胎剛度以及懸架剛度參數的影響明顯；橫向響應主要受到簧載質量、質心與車輛前、后軸之間的距離以及懸架阻尼影響；側傾響應主要受到簧載質量質心位置、懸架阻尼、輪距、簧載質量以及側傾轉動慣量影響。以上分析可知，B級車型在轉向盤大轉角ISO-C級路面激勵工況下，得出的結論與利用EE 方法在此工況下所獲的結論相似，但是方差分析方法相較于后者，靈敏度權重系數存在一定差異。

5 整車系統臺架試驗

為進一步驗證所設計雙層GSA 方法的有效性，此處基于已搭建整車半主動懸架測控平臺系統，以轉向盤轉角15°、車速40 km/h 的J-turn 實車行駛工況為例，對獲取的側傾角速度和橫擺率試驗數據，與整車觀測器仿真數據進行比較[13-14]，如圖6所示。

圖6 整車測試系統整體框架

利用上述測試平臺，在上述仿真類似工況下，利用整車模型關鍵參數對系統響應狀態估計結果進行驗證。同時，為進一步說明利用所設計雙層GSA 方法對實車系統響應結果與整車觀測器得到的側傾角速度與橫擺率之間的差異，引入標準偏差對數據結果進行對比，如表4所示。

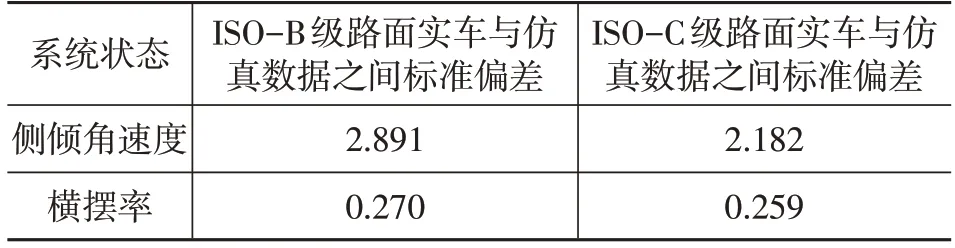
表4 實車數據與整車觀測器仿真數據標準偏差對比

由表4可知，ISO-C級路面側傾角速度標準偏差較ISOB級路面小。綜合以上仿真與試驗驗證結果可知，所設計的雙層GSA方法在整車狀態識別影響方面有較好效果。

6 結束語

本文基于雙層全局靈敏度分析方法對車輛懸架系統響應狀態及其動態特性進行定量分析并試驗驗證，進而為基于關鍵參數的車輛系統底盤控制提供一定的理論與實踐參考，主要得出以下結論：

a.所提出的雙層GSA 方法采用的靈敏度指標對車輛速度和車輛類型具有較好魯棒性。

b.ISO-B 級與ISO-C 級路面系統響應狀態對應的標準偏差不高于3，驗證了雙層GSA方法的有效性。