預應力UHPC-NC組合梁抗彎承載力計算方法

朱勁松，秦亞婷，史騰

(1.天津大學 建筑工程學院，天津，300072；2.天津大學 濱海土木工程與安全教育部重點實驗室，天津，300072)

超高性能混凝土(UHPC)是一種新型高性能纖維增強水泥基復合材料。與傳統的普通混凝土(NC)相比，UHPC具有優異的力學性能，如超高的抗壓強度和抗拉強度、低滲透性、高耐久性等[1-3]。部分或全部采用UHPC材料可以改善橋梁結構的性能[4]，將預制UHPC 梁單元與NC 橋面板通過抗剪連接件連接組成的UHPC-NC組合梁橋可以充分發揮UHPC的抗拉性能及NC的抗壓性能，同時提高結構的承載能力和耐久性，優化橋梁上部結構尺寸，并減輕結構自重。該結構形式在充分利用UHPC 優良性能的同時降低了造價，成為適用于中、小跨徑橋梁的新型結構形式。

VOO 等[5-6]介紹了由UHPC 預制梁和現澆NC橋面板構成的組合公路橋的制作工藝、施工順序以及設計方法；李昭等[7]提出了一種新型裝配式雙工字型UHPC-NC組合梁結構，并進行了縮尺模型試驗和有限元分析，研究了配筋率、UHPC 抗拉、壓強度及橋面板強度等級對組合梁抗彎性能的影響；季文玉等[8]通過試驗方法研究了活性粉末混凝土(RPC)應用于梁結構疊合梁的抗彎延性性能，研究結果表明RPC 材料優異的力學性能以及鋼纖維的存在提高了疊合梁峰值荷載后的變形能力；LI等[9]對UHPC-NC 疊合梁的抗彎性能進行了試驗和理論研究，發現將UHPC應用于預應力混凝土梁的受拉區，可以顯著提高構件的剛度和延性。現有研究已表明UHPC組合結構具有良好的力學性能及工程應用價值，然而，目前國內仍缺乏有效指導UHPC組合結構設計的規范。

為有效預測預應力UHPC-NC組合梁的抗彎承載力，指導UHPC-NC組合梁橋的設計，本文作者提出預應力UHPC-NC組合梁的抗彎承載力計算方法；建立預應力UHPC-NC組合梁的抗彎承載力理論計算公式，并將公式計算值與有限元模擬值進行對比，以驗證抗彎承載力計算公式的適用性。

1 預應力UHPC-NC組合梁概況

預應力超高性能混凝土-普通混凝土(UHPCNC)組合梁由預制工字型UHPC梁單元和覆蓋于其上的NC翼緣板通過預埋在UHPC梁單元中的抗剪鋼筋連接組成，以下簡稱為預應力UHPC-NC組合梁。預應力UHPC-NC組合梁可以減少鋼筋用量和構件截面尺寸，降低結構自重，在大跨度和重荷載結構應用中有明顯的優勢。預應力UHPC-NC組合梁結構示意如圖1所示。預制UHPC梁單元頂緣預留鋼筋連接件，豎向抗剪鋼筋伸出預制UHPC梁頂緣兼作鋼筋連接件，實現與現澆NC翼緣板間的剪力連接。

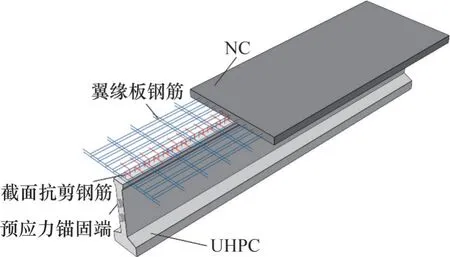
圖1 預應力UHPC-NC組合梁示意圖Fig.1 Schematic diagram of prestressed UHPC-NC composite beam

2 預應力UHPC-NC 組合梁有限元分析

2.1 材料本構模型

預應力UHPC-NC 組合梁的材料模型包括UHPC、普通混凝土、預應力筋、普通鋼筋模型。2.1.1 UHPC本構模型

UHPC 的受壓應力-應變關系采用文獻[10]提出的UHPC 受壓本構模型，其應力-應變關系曲線如圖2(a)所示，表達式如下：

式中：σ為UHPC 受壓應力；ε為UHPC 受壓應變；fc為UHPC 軸心抗壓強度；ε0為UHPC 的峰值壓應變；UHPC應變比ξ=ε/ε0；UHPC受壓峰值應變n=E0/Esl；應力峰值點的切割模量Esl=fc/ε0；E0為初始彈性模量。

UHPC的受拉應力-應變關系采用文獻[11]提出的UHPC受拉本構模型，其應力σ-應變ε關系曲線如圖2(b)所示，其中fct為UHPC應變硬化階段平均應力；εca為線性偏離初裂應變；εpc為極限應變。

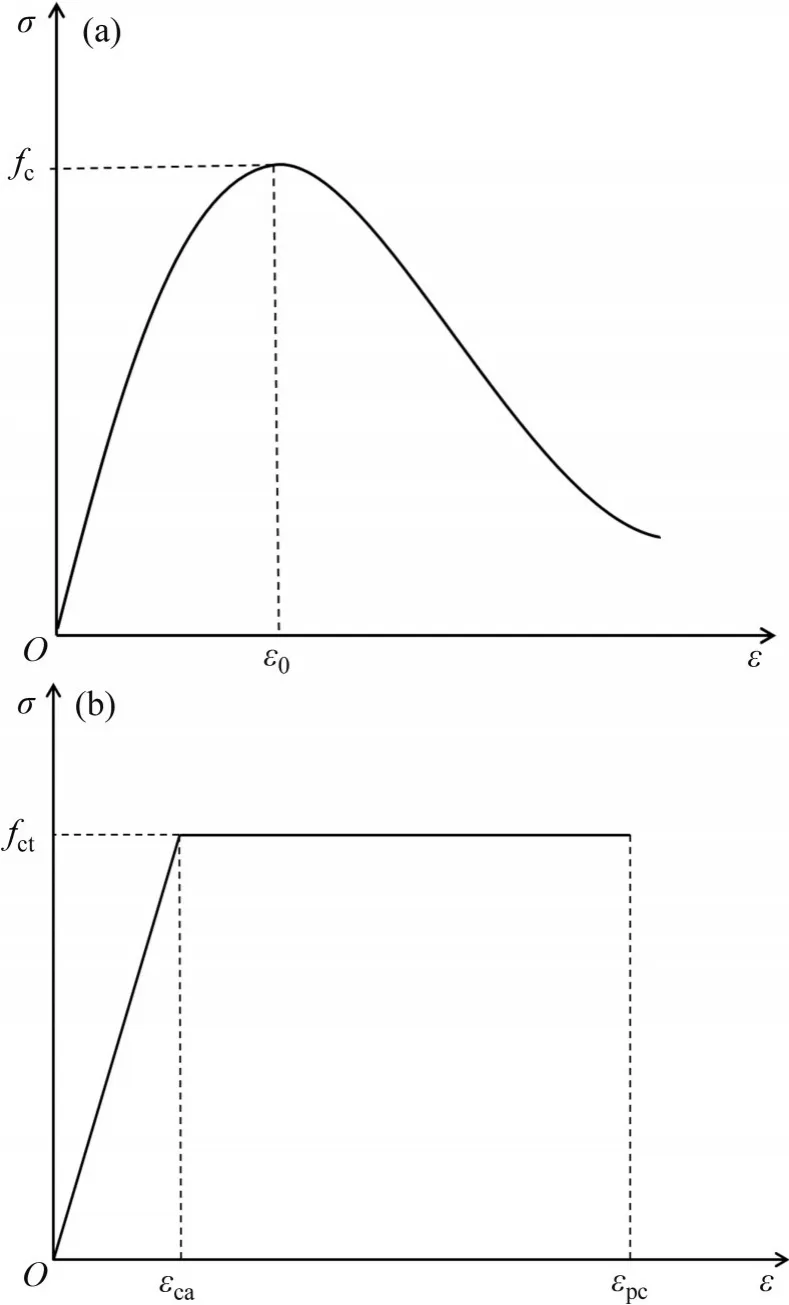
圖2 UHPC應力-應變關系曲線Fig.2 Stress-strain relationship curves of UHPC in compression and tension

2.1.2 NC本構模型

NC的單軸受壓應力-應變關系表達式如下：

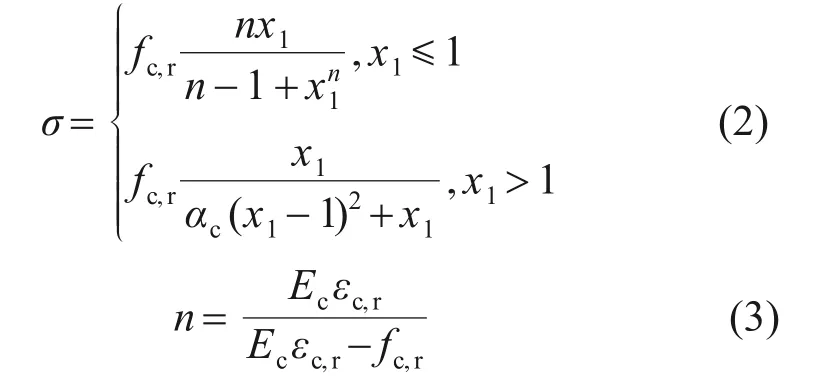
式中：fc，r為軸心受壓強度；εc，r為與fc，r對應的混凝土峰值壓應變；Ec為混凝土彈性模量；αc為混凝土單軸受壓應力-應變曲線下降段的參數，αc=0.157fc0.785-0.905；NC單軸受壓應變比x1=ε/εc，r。

NC的單軸受拉應力-應變關系表達式如下：

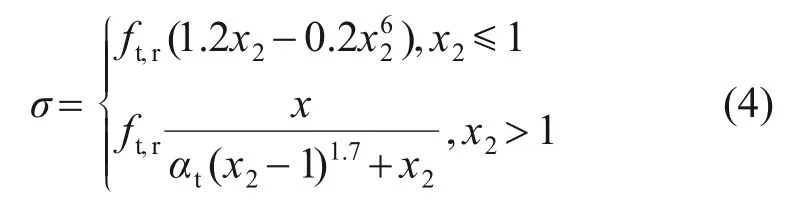
式中：ft，r為軸心受拉強度；εt，r為與ft，r對應的混凝土峰值拉應變；αt為混凝土單軸受拉應力-應變曲線下降段的參數，αt=0.312f2t，r；NC 單軸受拉應變比x2=ε/εt，r。

2.1.3 普通鋼筋本構模型

鋼筋本構采用理想彈塑性模型，其應力-應變關系表達式如下：

式中：Es為鋼筋彈性模量；fy為鋼筋的屈服強度；εy為鋼筋達到屈服強度時對應的峰值拉應變。

2.1.4 預應力筋本構模型

預應力鋼絞線本構關系采用雙斜線彈塑性模型，其應變-應力關系表達式如下：

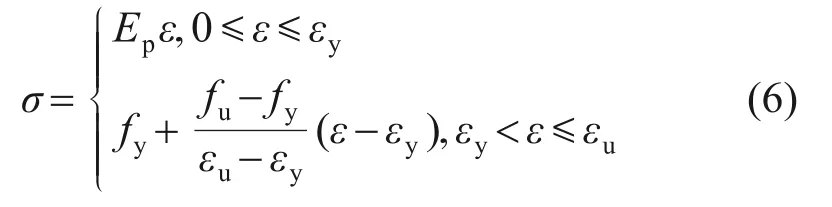
式中：fy為預應力鋼絞線屈服強度；fu為預應力鋼絞線極限強度；εu為極限拉應變；Ep為鋼絞線彈性模量。

本文在ABAQUS 中采用塑性損傷模型(damaged plasticity)模擬UHPC 和NC 的材料性能，混凝土塑性損傷模型中除定義材料本構關系外，還需確定與塑性準則等相關的參數，根據ABAQUS手冊中的推薦值，定義膨脹角為30°，偏心系數為0.1，雙軸抗壓強度與單軸抗壓強度之比為1.16，不變應力比為0.666 7，黏性系數為0.001。

2.2 UHPC-NC界面模擬方法

UHPC 與NC 均為水泥基材料，材料性質相近，UHPC-NC 界面黏結性能良好[12-13]。然而，對于UHPC-NC界面行為的模擬，現有研究中還沒有統一的方法。ABAQUS 中提供了多種模擬界面行為的選項，其中主要包含以下3種：1) 使用完全黏結(tie)對界面行為進行模擬，這種模擬方式認為2個接觸面之間不會發生相對滑移[14]；2) 采用默認的法向硬接觸和切向摩擦因數相結合的方式對界面行為進行模擬，該方法計算時忽略了界面間的黏聚力影響，僅考慮了界面間摩擦因數的影響，會低估界面間的黏結強度[15]；3) 采用接觸-分離模型(黏聚力模型)模擬界面的接觸行為，該模型同時考慮了界面間的黏聚力和摩擦因數的影響，是一種較為理想的接觸設置方式[16]。

本文分別采用以上3 種方法對文獻[7]中的UHPC-NC 組合梁縮尺模型進行有限元建模，其中接觸-分離模型采用最常用的雙線性本構模型。3種UHPC-NC界面模擬方式下得到的有限元模擬結果如圖3 所示。由圖3 可見：使用完全黏結(tie)以及采用接觸-分離模型(黏聚力模型)對界面行為進行模擬得到的有限元計算結果均能較好地與試驗結果吻合，但采用接觸-分離模型模擬時，計算成本較高。經綜合考慮，本文采用完全黏結(tie)模型對UHPC-NC界面行為進行模擬。

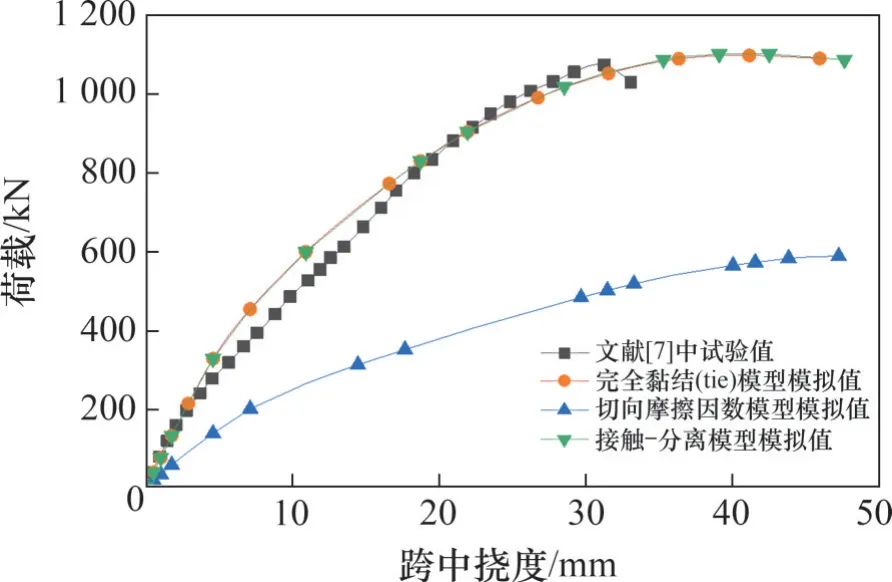
圖3 組合梁界面模擬方法對比Fig.3 Comparison of interface simulation methods for composite beams

2.3 試驗驗證

李昭等[7]根據實際工程尺寸設計了一根縮尺比例為1∶2 的UHPC-NC 組合梁模型，并進行了抗彎試驗，以研究UHPC-NC組合梁的抗彎性能。試驗梁總長7.5 m，橋面板寬度為580 mm，試驗梁上部采用現澆C50普通混凝土，現澆橋面板配筋為兩層直徑為8 mm 的縱橫向鋼筋，箍筋采用直徑為10 mm的單肢箍，東西兩側間距分別為100 mm和50 mm，下翼緣配筋為直徑為20 mm 的受拉主筋，鋼筋型號均為HRB400。

李立峰等[17]設計了一根大比例預應力UHPC-T形梁，并進行了抗彎試驗，以研究預應力UHPC梁的抗彎性能。試驗梁總長10 m，計算跨徑9.8 m，試驗梁采用后張預應力構件，上下翼緣分別布置5根和8根直徑均為12 mm的縱向鋼筋，箍筋采用直徑為12 mm 的單肢箍，間距為100 mm，鋼筋型號均為HRB335，下翼緣配筋為2束直線1860級預應力鋼絞線。

通過有限元分析軟件ABAQUS 建立文獻[7]中UHPC-NC 組合梁和文獻[17]中預應力UHPC-T 形梁的數值分析模型，材料力學性能分別見表1和表2，并進行單元選取、相互作用及邊界條件設定及網格劃分。采用完整的三維模型進行建模，NC和UHPC 采用八節點實體單元(C3D8R)建模。對于試件中的縱向鋼筋及預應力筋，采用兩節點桁架單元(T3D2)建模，鋼筋保護層厚度為25 mm，網格尺寸為50 mm。邊界使用簡支條件建模，采用位移控制加載。混凝土與鋼筋骨架采用嵌入(embedded)連接方式，混凝土與墊塊之間采用完全黏結(tie)連接，UHPC 與普通混凝土之間采用完全黏結(tie)連接。

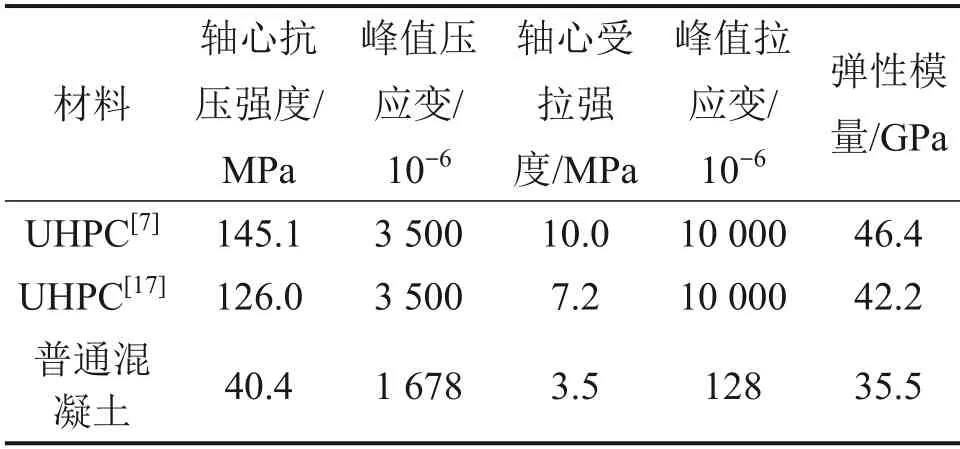
表1 UHPC及普通混凝土基本力學性能Table 1 Basic mechanical properties of UHPC and concrete

表2 鋼筋基本力學性能Table 2 Basic mechanical properties of reinforcement

將ABAQUS 有限元模擬結果與抗彎試驗結果進行對比，從而驗證有限元數值模擬方法的準確性。UHPC-NC 組合梁及預應力UHPC-T 形梁有限元計算得到的荷載-跨中撓度曲線與試驗曲線的比較如圖4所示。由圖4可知，本文有限元模擬結果與抗彎試驗結果吻合良好，驗證了本文所建立的UHPC-NC 組合梁和預應力UHPC-T 形梁有限元模型的準確性和可靠性。

圖4 荷載-跨中撓度有限元計算曲線與試驗曲線比較[7,17]Fig.4 Comparison of finite element calculation curves and experimental curves of load-deflection[7,17]

3 預應力UHPC-NC 組合梁抗彎性能分析

3.1 預應力UHPC-NC組合梁數值模型

本文預應力UHPC-NC組合梁總長為30 m，梁肋下部布置5 根直徑為25 mm 的受拉主筋。混凝土橋面板中橫向鋼筋鋪設間距為500 mm，縱向鋼筋間距為100 mm，鋼筋直徑均為16 mm。箍筋為直徑為16 mm 的單肢箍筋，箍筋間距為100 mm。鋼筋規格均為HRB400。采用2 束?s15.2-6(每束包含6 根直徑為15.2 mm 的鋼絞線)的1860 級鋼絞線作為預應力筋，預應力筋張拉控制應力為1 395 MPa。預應力UHPC-NC 組合梁尺寸構造如圖5所示。

圖5 預應力UHPC-NC組合梁構造圖Fig.5 Structure diagram of prestressed UHPC-NC composite beam

對預應力UHPC-NC 組合梁進行受彎模擬分析，其中UHPC和NC材料參數采用文獻[7]中的實測值。預應力UHPC-NC 組合梁計算模型如圖6所示。

圖6 預應力UHPC-NC組合梁有限元模型Fig.6 FE model of prestressed UHPC-NC composite beam

3.2 破壞模式

對于預應力UHPC結構，由于UHPC在開裂之后仍然具有一定的抗拉強度，預應力筋不會立即屈服，結構不會發生脆性破壞[17]。根據NC壓碎和預應力筋屈服及拉斷發生的先后順序不同，預應力UHPC-NC組合梁破壞模式可分為超筋梁脆性破壞和適筋梁破壞，當結構配筋率過大時，會導致受壓區NC壓碎時預應力筋未屈服，發生超筋梁破壞。適筋梁塑性破壞又可分為受壓區混凝土壓碎破壞和預應力筋拉斷破壞。當配筋適當時，預應力筋屈服后，受壓區混凝土壓碎先于預應力筋拉斷發生，受壓區混凝土發生壓碎破壞；反之，則發生預應力筋拉斷破壞。

對于預應力UHPC-NC組合梁，跨中截面受壓混凝土應變及受拉預應力筋應變與跨中撓度的關系如圖7所示，預應力筋應力隨跨中撓度變化如圖8 所示。由圖7 與圖8 可見：當受壓區混凝土達到極限壓應變0.003 時，組合梁預應力筋應力fps為1 813 MPa，組合梁預應力筋已經屈服，但預應力筋尚未達到極限拉應變εpu=0.035，說明組合梁預應力筋屈服后，受壓區混凝土壓碎先于預應力筋拉斷發生，表現為受壓區混凝土被壓碎破壞。

圖7 應變與撓度關系曲線Fig.7 Relationship curve between strain and deflection

圖8 預應力筋應力變化曲線Fig.8 Stress variation curve of prestressed tendon

3.3 參數分析

本文系統地分析了預應力筋配筋率、普通鋼筋直徑、普通鋼筋強度等級以及高跨比等參數對預應力UHPC-NC組合梁抗彎承載能力的影響。預應力UHPC-NC組合梁參數以及本文抗彎承載力公式計算結果與有限元計算結果對比見表3。參數變化對預應力UHPC-NC 組合梁抗彎性能的影響見圖9。

由表3和圖9可知，提高預應力筋配筋率、普通鋼筋直徑和高跨比均可顯著提高預應力UHPCNC組合梁極限抗彎承載力，普通鋼筋強度等級對組合梁極限抗彎承載力影響不明顯；組合梁開裂前的抗彎性能受高跨比影響較大，增大高跨比可以有效提高組合梁彈性階段抗彎剛度；預應力筋配筋率、普通鋼筋直徑和普通鋼筋強度等級對組合梁開裂前的受彎性能沒有顯著影響。

圖9 各參數變化對預應力UHPC-NC組合梁抗彎性能的影響Fig.9 Influences of various parameters on the flexural performance of prestressed UHPC-NC composite beams

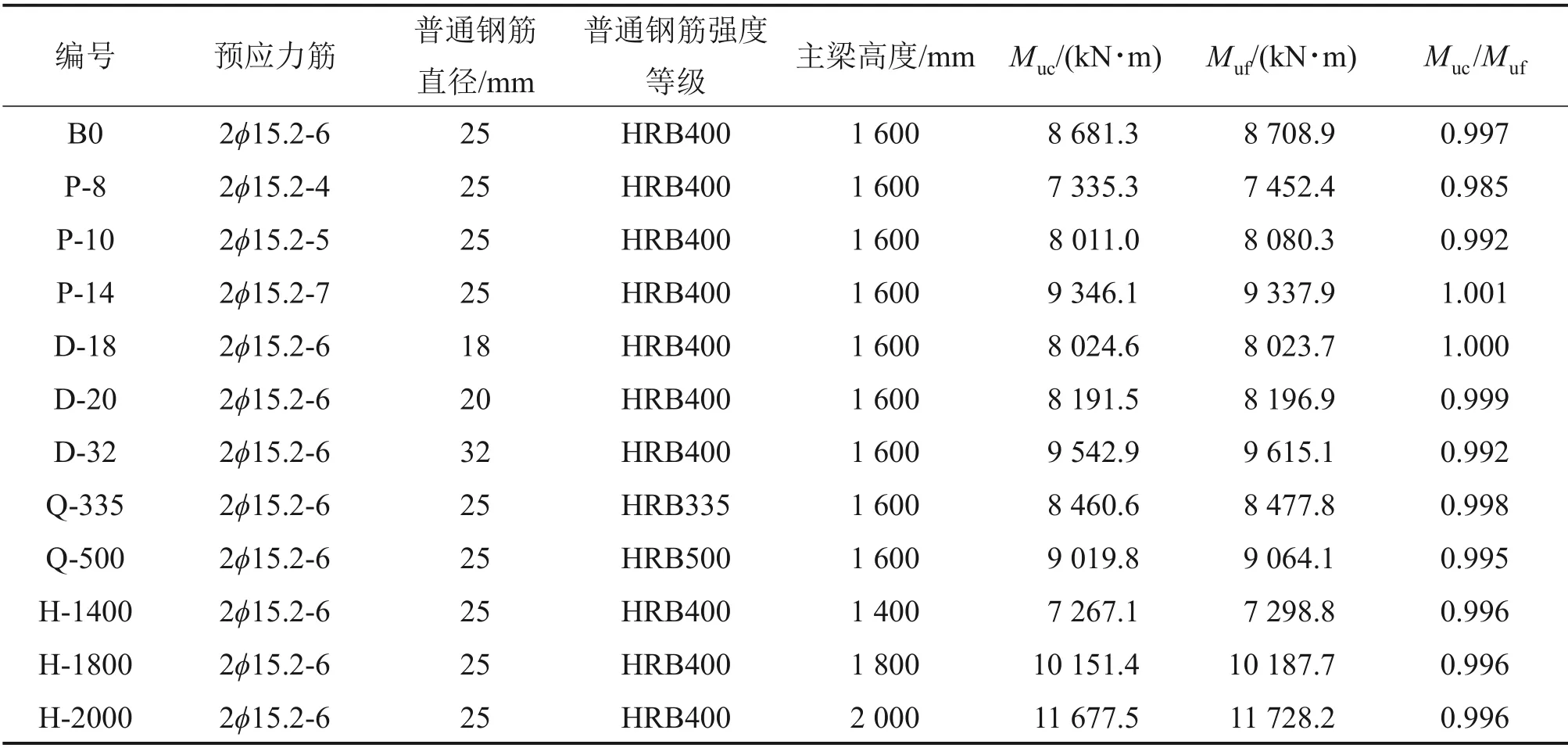
表3 組合梁參數信息以及抗彎承載力公式計算結果與有限元計算結果對比Table 3 Composite beam parameter information and comparison of calculation results with finite element calculation results of flexual capacity

4 受彎承載力分析

4.1 基本假定

與一般鋼筋混凝土梁類似，計算預應力UHPC-NC 組合梁抗彎承載力時，采用以下基本假設：1) NC翼緣板和預制UHPC梁單元之間存在可靠連接，相對滑移很小，可以忽略不計；2) 組合

梁截面上UHPC、NC、預應力筋和鋼筋應變均符合平截面假定；3) 當組合梁達到極限狀態時，受壓區混凝土部分已進入塑性狀態，將截面受壓區NC 和UHPC 應力圖形簡化為矩形，壓應力分別取為NC 和UHPC 的軸心抗壓強度；4) 考慮受拉區UHPC對抗彎承載力的貢獻，將受拉區UHPC應力圖形簡化為矩形，其拉應力基于安全考慮取為λ倍抗拉強度(λ≤1)，其中λ為受拉區UHPC等效矩形應力系數[18]，受拉區等效矩形拉應力為λftd，其中，ftd為UHPC抗拉強度。

將組合梁截面進行簡化處理，將上翼緣承托部分和下翼緣馬蹄處按等面積原則簡化為矩形截面。基于上述假定，承載力極限狀態時UHPC-NC組合截面應力應變分布如圖10所示。

圖10 中，M為組合梁抗彎承載力；hf1為普通混凝土受壓翼緣高度；bf1為普通混凝土受壓翼緣寬度；bf2為受拉UHPC 翼緣寬度；hf2為受拉UHPC 翼緣高度；b為UHPC-NC 組合截面腹板寬度；h為UHPC-NC 組合截面高度；fsd為縱向普通鋼筋的抗拉強度設計值；As為受拉區縱向普通鋼筋面積；f′sd為縱向普通鋼筋的抗壓強度設計值；A′s為受壓區縱向普通鋼筋面積；ftd為UHPC軸心抗拉強度；fcd為UHPC 軸心抗壓強度設計值；fcd1為普通混凝土軸心抗壓強度設計值；fpd為縱向預應力鋼筋的抗拉強度設計值；Ap為受拉區縱向預應力鋼筋的截面面積。β為受彎構件受壓區高度x與實際受壓區高度xc的比值，對于C50 混凝土，取0.8[19]；xt為組合梁受拉區等效高度；對于UHPC結構，參考“公路橋涵超高性能混凝土應用規范(征求意見稿)”取0.82；對于組合截面本文統一取為0.82。

圖10 組合梁截面應力-應變分布圖Fig.10 Stress-strain distribution of cross section of composite beams

4.2 抗彎承載力計算方法

在計算截面的極限彎矩時，應先判斷所屬的截面類型，根據受壓區高度不同，受拉區和受壓區的合力計算以及極限抗彎承載力的計算分為以下2 種情況：當受壓區高度在NC 翼緣板內，截面為第一類截面；當受壓區進入UHPC腹板區域，截面為第二類截面。

當滿足式(7)時，受壓區高度在NC 翼緣板內，抗彎承載力按第一類截面計算，截面簡化應力分布如圖11所示。

圖11 組合梁第一類截面簡化應力分布Fig.11 Simplified stress distribution of the first section of composite beams

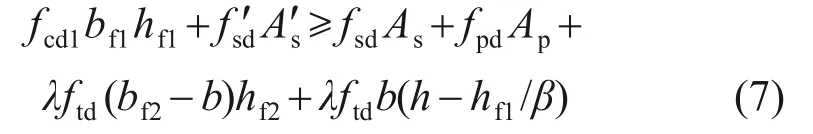
由力的平衡條件可求出受壓區高度x：

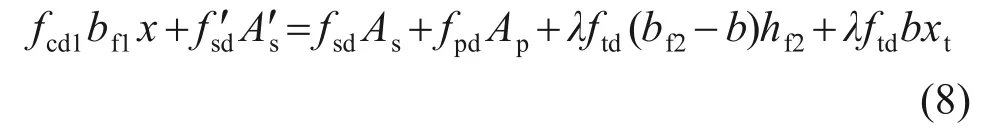
受拉區等效高度xt按下式計算：

對梁底受拉邊緣取矩可得抗彎承載力Mu：

式中：as為受拉區普通鋼筋合力點到受拉區邊緣的距離；a′s為受壓區普通鋼筋合力點到受壓區邊緣的距離；ap為受拉區預應力筋合力點到受拉區邊緣的距離。

當不滿足式(7)時，受壓區高度在UHPC 腹板內，抗彎承載力按第二類截面計算，截面簡化應力分布如圖12所示。

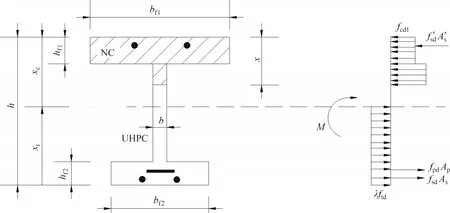
圖12 組合梁第二類截面簡化應力分布Fig.12 Simplified stress distribution of the second section of composite beams

由力的平衡條件可求出受壓區高度x：

對梁底受拉邊緣取矩可得抗彎承載力Mu：

4.3 受拉區UHPC等效矩形應力系數取值比例

預應力UHPC-NC組合梁正截面抗彎承載力計算與普通鋼筋混凝土梁不同，需要考慮受拉區UHPC抗拉強度對抗彎承載力的貢獻。通過前面的分析可知，在計算組合梁抗彎承載力時，受拉區UHPC 的應力等效為矩形應力圖，基于安全考慮，提出受拉區UHPC 等效矩形應力系數λ，當λ取值為0～1.0 時，預應力UHPC-NC 組合梁正截面抗彎承載力公式計算值與有限元模擬值比較如表4和圖13所示。圖13中，實線表示Mu公式計算值與有限元模擬值之比為1，虛線范圍表示Mu公式計算值與有限元模擬值的相對誤差小于20%[20]。

表4 不同λ下Mu公式計算結果與有限元計算結果對比Table 4 Comparison between calculation results of different UHPC tensile strength ratio and FE calculation results of Mu

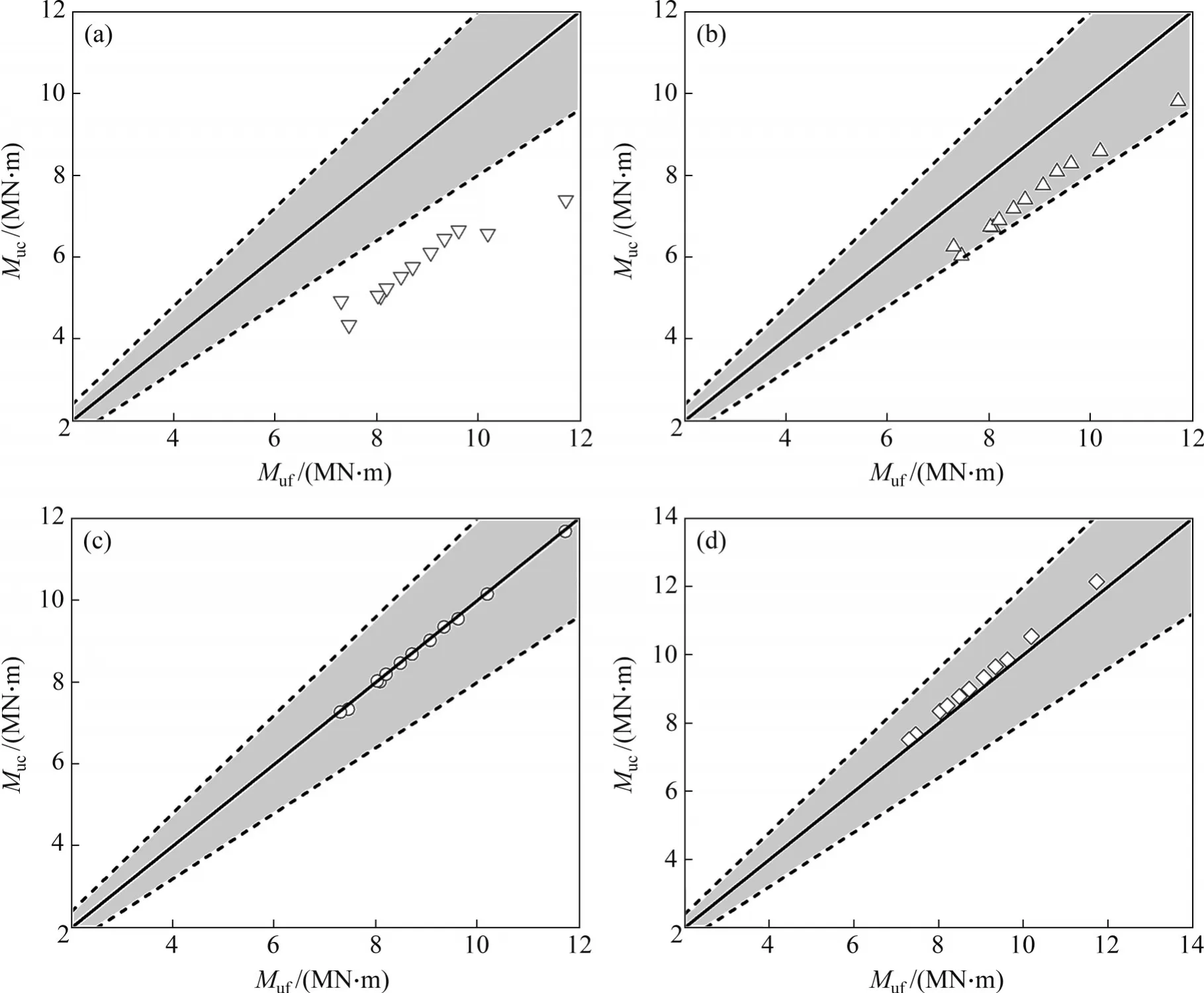
圖13 Mu公式計算值與有限元計算值對比Fig.13 Comparison between the calculated values of the formula and the calculated values of the FE of Mu

由表4和圖13可知：當受拉區UHPC等效矩形應力系數為0即不考慮受拉區UHPC對抗彎承載力的貢獻作用時，抗彎承載力公式計算值與有限元模擬值比值的均值為64.9%，標準差為0.03，抗彎承載力公式計算結果過于保守；當受拉區UHPC等效矩形應力系數為0.1～0.8 時，抗彎承載力公式計算值與有限元模擬值比值的平均值為68.9%～95.8%，標準差區間為0.006～0.027，抗彎承載力公式計算結果偏保守；當受拉區UHPC等效矩形應力系數為0.9時，抗彎承載力公式計算值與有限元模擬值比值的平均值為99.6%，標準差為0.004，抗彎承載力公式計算值與有限元模擬值吻合良好；當受拉區UHPC 等效矩形應力系數為1.0 時，抗彎承載力公式計算值與有限元模擬值比值的平均值為103.3%，標準差為0.004，抗彎承載力公式計算結果偏大，設計值安全性偏低。經綜合考慮，設計時取受拉區UHPC等效矩形應力系數λ=0.9。

5 結論

1) 基于UHPC-NC界面模擬方法的研究，建立了預應力UHPC-NC組合梁的有限元分析模型，并通過試驗驗證了模擬方法的準確性和可靠性。提高預應力筋配筋率、普通鋼筋直徑和高跨比均可顯著提高組合梁極限抗彎承載力，普通鋼筋強度等級對組合梁極限抗彎承載力影響不明顯。

2) 基于平截面假定、截面平衡條件以及UHPC、普通混凝土、預應力筋和鋼筋的本構關系，提出了預應力UHPC-NC組合梁的抗彎承載力計算公式。通過有限元分析驗證了計算公式的準確性和可靠性，抗彎承載力公式計算值與有限元模擬值比值的均值為99.6%，標準差為0.004，表明本文所推導出的抗彎承載力計算公式具有較高的精度。

3) 當預應力UHPC-NC組合梁達到極限承載力時，考慮受拉區UHPC對抗彎承載力的貢獻，提出了受拉區UHPC 等效矩形應力系數λ，當λ取0.9時，抗彎承載力公式計算值與有限元模擬值吻合良好。