地鐵直線段鋼彈簧浮置板軌道鋼軌波磨萌生原因及參數影響分析

錢彥行,蔡成標,楊昀,何慶烈,朱勝陽

(西南交通大學牽引動力國家重點實驗室,成都 610031)

1 概述

隨著城市軌道交通的快速發展，地鐵線路部分區間出現鋼軌異常磨耗現象。鋼軌波磨是一種沿鋼軌表面縱向分布的典型諧波形激擾，它會惡化輪軌動態相互作用，引起曲線嘯叫[1-2]，影響乘客乘坐舒適性，且易引發系統共振導致一系鋼簧、扣件疲勞斷裂問題，降低行車安全性[3]。因此分析鋼軌波磨產生機理，從而制定相應的緩解措施具有重要意義。

GRASSIE[4-5]、金學松[6]、朱海燕[7]和關慶華[8]等學者對不同時期的鋼軌波磨研究進展進行了詳細綜述。上述綜述文獻均指出鋼軌波磨形成與軌道系統振動特性相關性較大，而軌道系統振動特性又受軌道結構類型影響較大[9-11]。李偉[12]為研究克隆蛋扣件軌道系統出現的鋼軌波磨現象與軌道振動特性之間的關系，通過建立科隆蛋扣件軌道有限元模型對其動態特性進行仿真計算，得出鋼軌波磨的產生與軌道系統垂向振動模態密切相關。李偉等[13]以相同研究思路對地鐵彈性短枕軌道出現的鋼軌波磨現象進行了分析，得出鋼軌波磨的產生與鋼軌相對軌枕發生垂向反共振有關。李霞[14]通過相同方法研究了曲線地段梯形軌枕軌道出現的鋼軌波磨現象，研究發現鋼軌相對梯形軌枕的垂向及橫向彎曲振動是導致鋼軌波磨的關鍵因素。MA[15]為研究高速鐵路直線段出現波長65～80 mm和125～150 mm的鋼軌波磨現象，建立了包含柔性輪對的車輛-軌道耦合動力學模型，通過分析研究發現鋼軌波磨的產生與鋼軌pinned-pinned共振及鋼軌三階垂向彎曲振動模態有關。本文同樣從軌道系統振動角度出發，針對某地鐵直線地段鋼彈簧浮置板道床軌道出現的波長為160～250 mm鋼軌波磨現象[16]，通過建立相應實尺寸有限元模型進行研究。

為分析軌道系統振動特性對輪軌動態接觸的具體影響，本文又基于有限元理論和車輛-軌道耦合動力學理論[17]，建立車輛-鋼彈簧浮置板軌道剛柔動力學模型以進行相關研究。然后運用該模型，以鋼軌磨耗功率為評價指標，定性地分析了軌道系統的扣件參數和鋼彈簧隔振器參數對鋼軌磨耗功率的影響。

2 數值模型

為研究某地鐵直線地段鋼彈簧浮置板軌道出現的波長為160～250 mm鋼軌波磨與輪軌動態接觸特性的關系及軌道系統參數變化對鋼軌磨耗功率的影響，本文建立了車輛-鋼彈簧浮置板軌道耦合動力學模型。

2.1 車輛-軌道耦合動力學模型建立

以地鐵B型車為例，基于多剛體動力學理論，建立了車輛動力學模型，模型考慮車體、轉向架和輪對的沉浮、點頭、搖頭和側滾運動。車輛系統主要參數見表1。

表1 車輛系統主要參數[16]

軌道系統由鋼軌、扣件、鋼彈簧浮置板道床及鋼彈簧隔振器組成。鋼軌采用可考慮剪切變形的Timoshenko梁來模擬。采用有限元軟件建立鋼彈簧浮置板道床有限元模型，通過選取合適邊界點計算其約束模態及自由模態，然后使用Craig-Bampton方法建立鋼彈簧浮置板道床動力學模型，模態階數取值50。扣件及鋼彈隔振器采用并聯的彈簧-阻尼結構來模擬。軌道系統參數見表2。

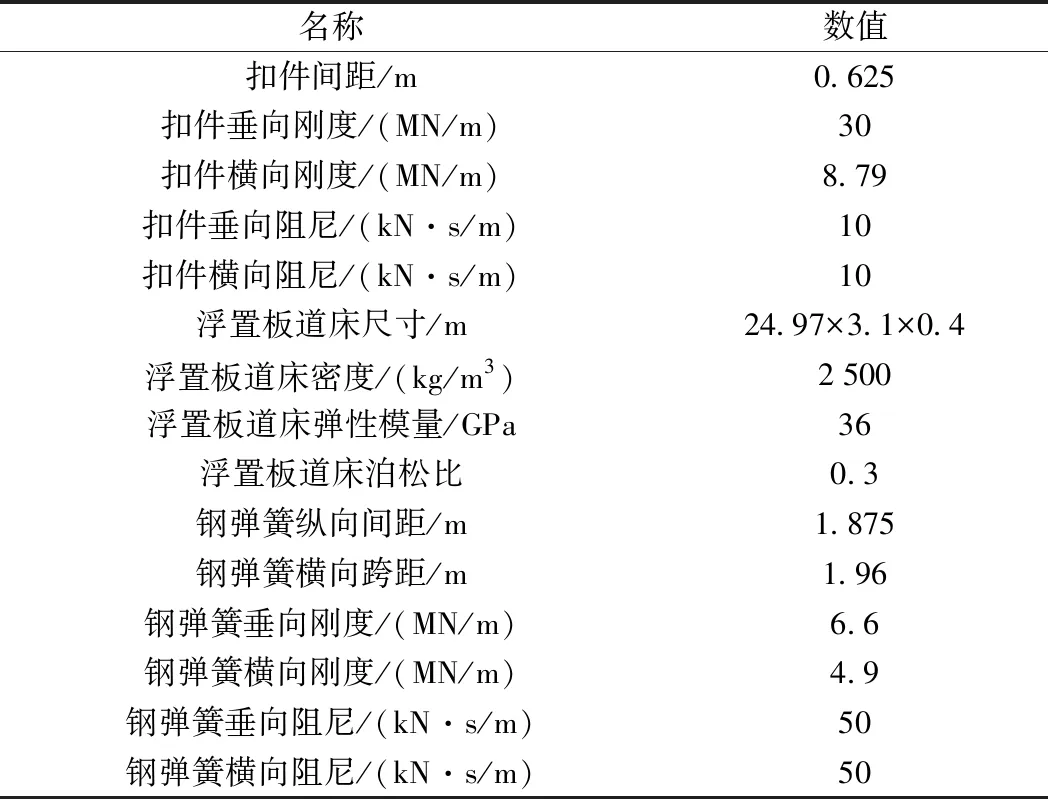
表2 軌道系統參數[16]

對于輪軌接觸部分，使用Kik-Piotrowski算法計算輪軌法向力，使用FASTSIM算法計算輪軌蠕滑力。至此車輛-鋼彈簧浮置板軌道空間耦合動力學模型建立完畢，圖1為車輛-鋼彈簧浮置板軌道耦合動力學模型。

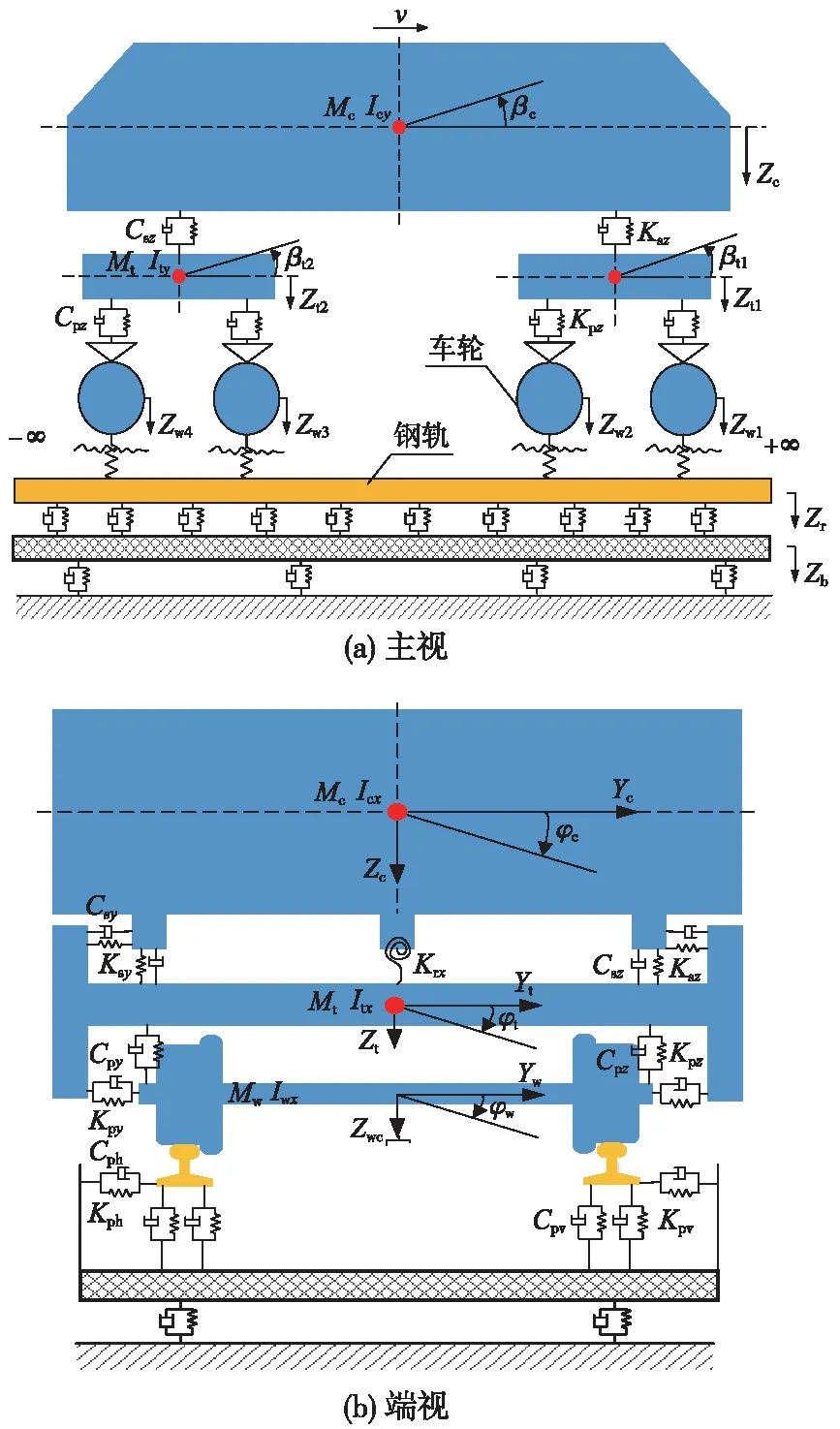
圖1 車輛-鋼彈簧浮置板軌道空間耦合動力學模型

2.2 鋼軌磨耗功率計算

以鋼軌波磨通過頻率處的磨耗功率來定性地描述波長為160～250 mm的鋼軌波磨發展速率，然后分析扣件參數及鋼彈簧隔振器參數變化對鋼軌波磨的影響。通過建立的車輛-鋼彈簧浮置板軌道空間耦合動力學模型獲取輪軌縱橫向蠕滑率/力，進而通過公式(1)計算鋼軌磨耗功率。

Fy(i，j)ξy(i，j))

(1)

式中，Fx為縱向蠕滑力；Fy為橫向蠕滑力；ξx為縱向蠕滑力；ξy為橫向蠕滑力。nx和ny分別為輪軌接觸斑縱橫向離散網格數量。

3 模型驗證

為驗證車輛-軌道耦合動力學模型的準確性，本文通過計算鋼軌的垂向位移導納和軌道板垂向振動加速度，并分別和發生波磨地段的實測鋼軌位移導納[16]、實測軌道板垂向振動加速度作對比。模型在進行動力學計算過程中軌道不平順使用實測地鐵軌道不平順，車速設置為65 km/h。圖2為鋼軌垂向位移導納特性實測與仿真對比結果，通過對比可知，實測與仿真的P2共振頻率與Pinned-Pinned共振頻率較為接近，實測與仿真得到的鋼軌位移導納曲線整體較為吻合。圖3為軌道板垂向振動加速度實測與仿真計算結果對比，由圖可知，實測與仿真計算結果整體吻合較好。經上述對比分析，驗證了車輛-軌道耦合動力學模型的準確性。

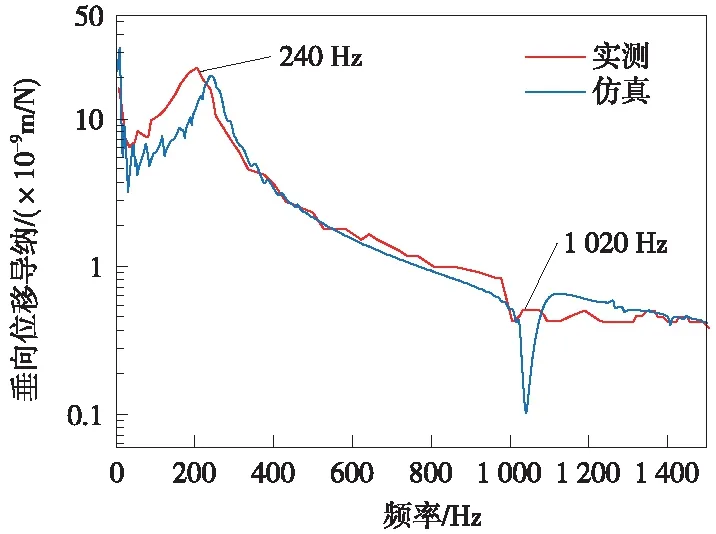
圖2 鋼軌垂向位移導納實測與仿真對比

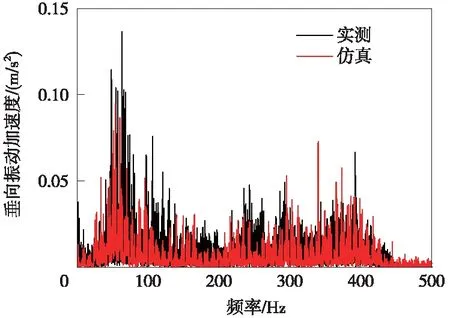
圖3 軌道板垂向振動加速度實測與仿真結果對比

4 鋼軌波磨與軌道振動特性關系

列車車速為65 km/h時，鋼軌波磨通過頻帶為72～112 Hz[16]。為分析鋼軌波磨產生與軌道結構振動特性之間關系，本節使用有限元軟件建立了實尺寸鋼彈簧浮置板軌道模型。鋼軌和軌道板采用實體單元Solid45單元模擬，扣件及鋼彈簧隔振器采用彈簧單元Combin14單元進行模擬，圖4為所建立的鋼彈簧浮置板軌道有限元模型。

鋼軌波磨通過頻帶內的軌道結構振動模態有第10～14階鋼軌橫向彎曲振動模態、第8階和第9階軌道板垂向彎曲振動模態及第6～8階扭轉振動模態。相關鋼軌橫向彎曲振動模態頻率分別為76，80，86，92 Hz和99 Hz；相關軌道板彎曲振動模態頻率分別為78.2 Hz和96.6 Hz；相關軌道板扭轉振動模態頻率分別為78.5，93.9 Hz和110.3 Hz。其中，鋼軌每階橫向彎曲振動模態表現為左右兩側鋼軌同向和反向兩種橫向彎曲振動形式。圖5為部分軌道結構振動模態。

圖4 鋼彈簧浮置板軌道有限元模型

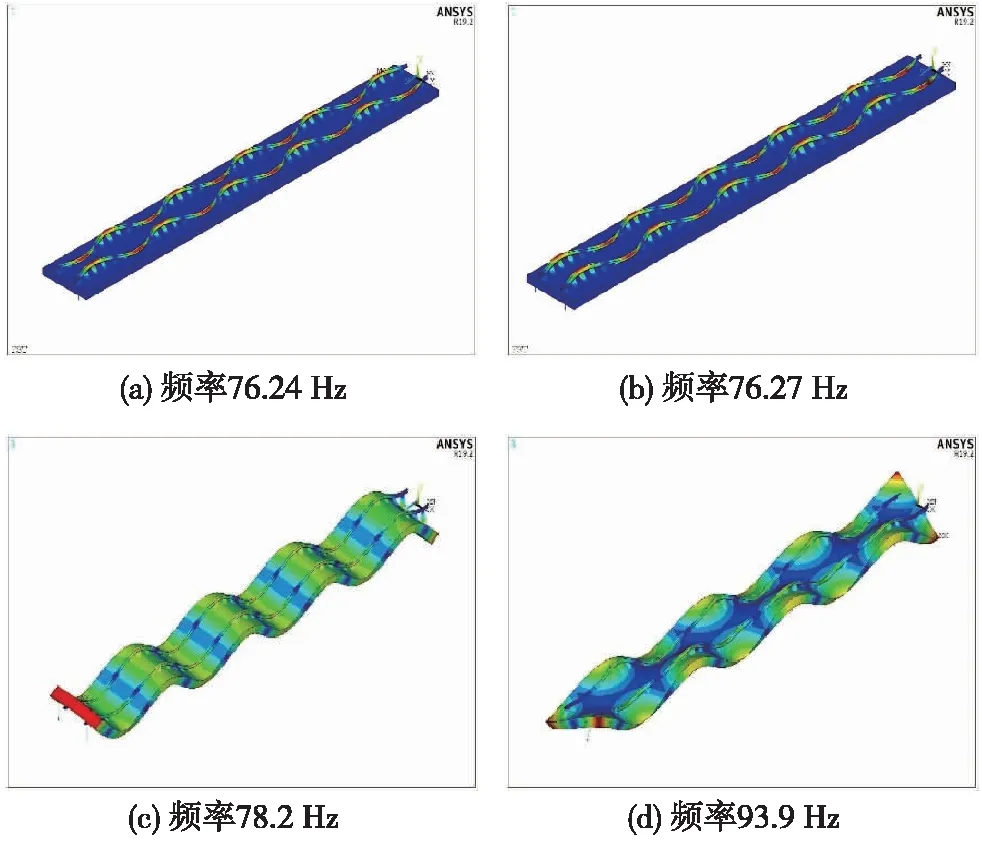
圖5 軌道結構部分振動模態

鋼軌波磨通過頻帶范圍內的軌道結構振動模態中以鋼軌橫向彎曲振動模態為主，從而易影響輪軌粘滑振動，所以上述多階軌道結構振動模態是導致直線地段鋼彈簧浮置板軌道出現特定波長鋼軌波磨的重要因素。在上述多階相關軌道結構振動模態參與輪軌耦合振動的情況下，下面借助車輛-鋼彈簧浮置板軌道剛柔耦合動力學模型研究軌道系統關鍵參數對鋼軌波磨發展的影響。

5 鋼軌波磨發展影響因素研究

文獻[18]指出，扣件系統參數(剛度或阻尼)的變化會改變輪軌力幅值及頻域分布，進而可能會影響鋼軌波磨發展特性。本文在鋼彈簧浮置板軌道幾何參數固定的情況下，為進一步分析扣件及鋼彈簧隔振器參數對鋼軌波磨發展特性的影響，下面使用建立的剛柔耦合動力學模型，以鋼軌磨耗功率為評價指標來進行分析。

5.1 隔振器剛度及阻尼影響分析

根據實際線路情況，本節設置鋼彈簧隔振器剛度KDV分別為5.3 MN/m和6.6 MN/m[19]，保持軌道系統其他參數不變，分析隔振器剛度變化對鋼軌波磨發展特性的影響。圖6為不同隔振器剛度下的鋼軌磨耗功率頻譜圖。由圖6可知，隔振器剛度的變化對磨耗功率影響可忽略。

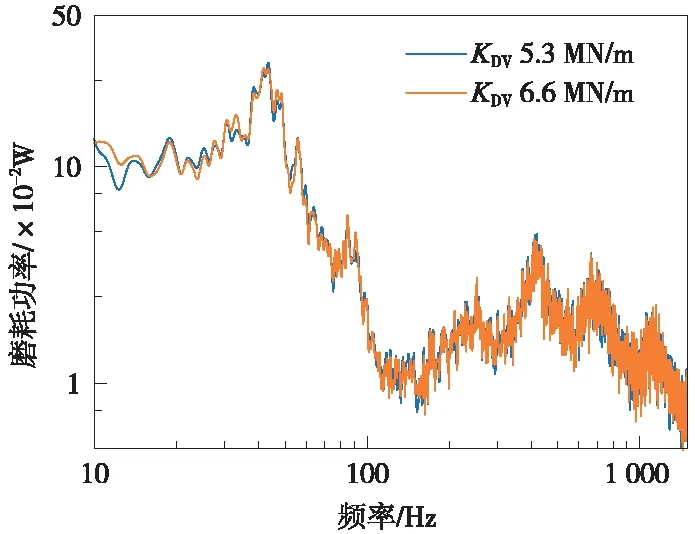
圖6 不同隔振器剛度下鋼軌磨耗功率頻譜

在保持隔振器剛度取值為6.6 MN/m時，隔振器阻尼CDV分別取10，20 kN·s/m和30 kN·s/m，保持軌道系統其他參數不變，分析隔振器阻尼變化對直線地段鋼彈簧浮置板軌道的鋼軌波磨發展特性的影響。圖7為不同隔振器阻尼下的磨耗功率頻譜圖。由圖7可知，隔振器阻尼的變化對鋼軌磨耗功率影響可忽略。

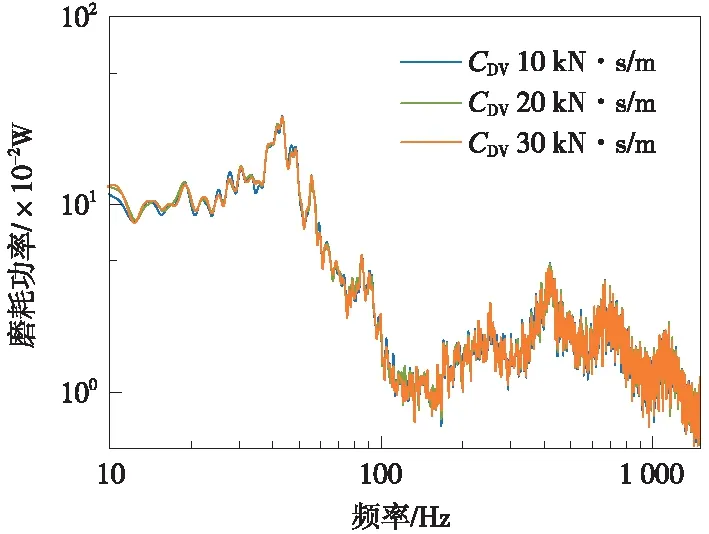
圖7 不同隔振器阻尼下鋼軌磨耗功率頻譜

鋼軌磨耗功率對隔振器剛度及阻尼變化敏感性較弱是因為隔振器剛度及阻尼變化主要影響浮置板低頻振動，浮置板低頻振動變化反饋至輪軌振動過程中經過扣件及鋼軌振動隔絕影響大幅減弱。由此可知，通過調整鋼彈簧隔振器參數來抑制直線地段鋼彈簧浮置板軌道鋼軌波磨發展不可行。

5.2 扣件垂向剛度影響分析

本節扣件垂向剛度Kpv分別取10，30，50，70 MN/m和100 MN/m[20]，保持軌道系統其他參數不變，分析扣件垂向剛度的變化對輪軌接觸特性及鋼軌波磨發展特性的影響。

圖8(a)和圖8(b)為不同扣件垂向剛度下縱向蠕滑率和橫向蠕滑率頻譜圖。由圖8(a)可知，20～30 Hz范圍內縱向蠕滑率隨扣件垂向剛度增大而減小，30～100 Hz范圍內縱向蠕滑率隨扣件垂向剛度增大而增大，當扣件垂向剛度取值70 MN/m以上時，鋼軌波磨通過頻帶處縱向蠕滑率峰值較為突出，100～300 Hz范圍內縱向蠕滑率隨扣件垂向剛度增大而減小；300～1 500 Hz范圍內縱向蠕滑率變化較小。

由圖8(b)可知，扣件垂向剛度的變化對25～300 Hz范圍內橫向蠕滑率影響較大，具體表現為：隨著扣件垂向剛度的減小，該頻段范圍內橫向蠕滑率減小。扣件垂向剛度在30～40 MN/m之間變化時，橫向蠕滑率對扣件垂向剛度變化敏感性較差。當扣件垂向剛度降至10 MN/m時，鋼軌波磨通過頻帶范圍內橫向蠕滑率峰值消失。

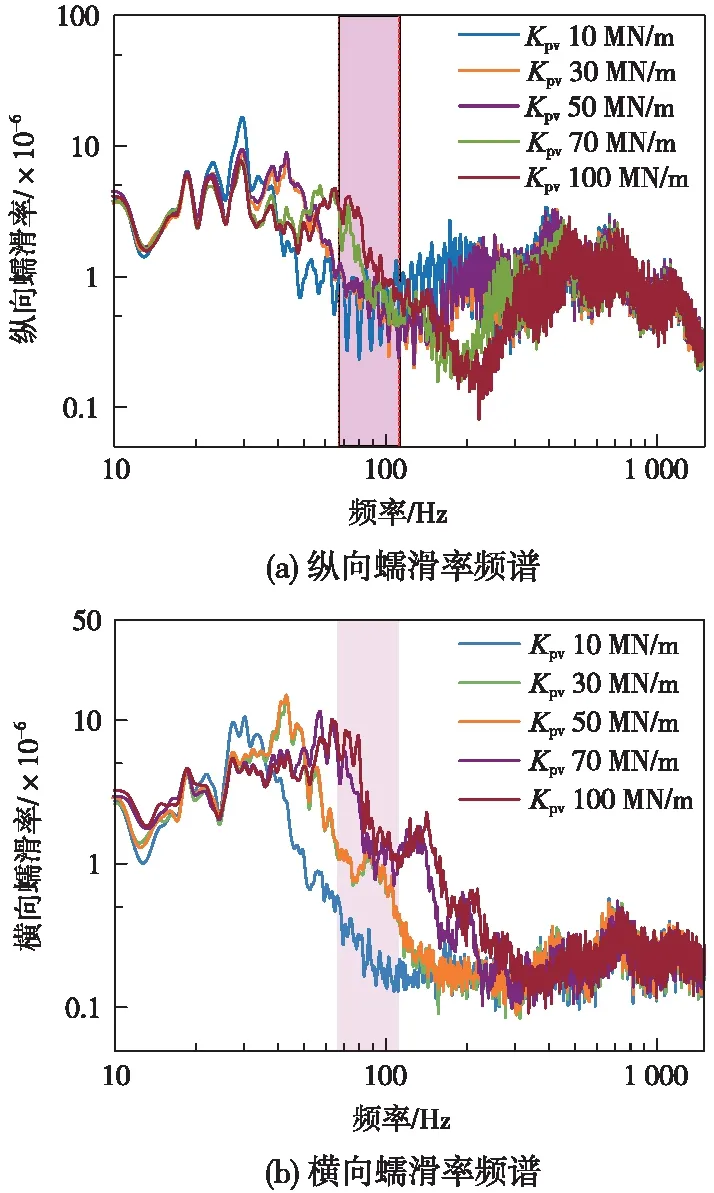
圖8 不同扣件垂向剛度下蠕滑率頻譜

圖9為不同扣件垂向剛度下磨耗功率頻譜圖。由圖可知，扣件垂向剛度變化對鋼軌磨耗功率影響與扣件垂向剛度變化對橫向蠕滑率的影響相似，當扣件垂向剛度降至30 MN/m以下時，鋼軌波磨通過頻帶處的共振峰值呈現消失趨勢。這是由于扣件剛度減小導致鋼軌波磨通過頻帶處縱橫向蠕滑率峰值消失引起。當扣件取值10 MN/m時，鋼軌垂向位移約為3.5 mm，鋼軌垂向位移幅值接近限值。綜上所述，在不影響行車安全性的前提下，可通過將扣件垂向剛度控制在10～30 MN/m來減緩鋼軌波磨發展速率。

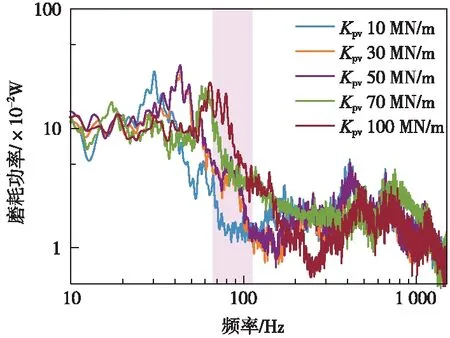
圖9 不同扣件垂向剛度下鋼軌磨耗功率頻譜

5.3 扣件垂向阻尼影響分析

本節扣件垂向阻尼Cpv分別取10，20 kN·s/m和30 kN·s/m，保持軌道系統其他參數不變，分析扣件垂向阻尼的變化對輪軌接觸特性及鋼軌波磨發展特性的影響。

圖10(a)和圖10(b)為不同扣件垂向阻尼下的縱向蠕滑率和橫向蠕滑率頻譜圖。由圖10(a)可知，隨著扣件垂向阻尼的增大，30～1 500 Hz范圍內縱向蠕滑率呈遞減趨勢，其中250，410，702 Hz和1 140 Hz處縱向蠕滑率減小較為明顯，當扣件垂向阻尼增至30 kN·s/m時，250 Hz處的共振現象明顯減弱。從圖10(b)可得出，隨著扣件垂向阻尼的增大，30～800 Hz范圍內橫向蠕滑率呈減小趨勢，72～112，410 Hz和702 Hz處的橫向蠕滑率衰減較為明顯。其中，當扣件垂向阻尼增至20 kN·s/m及以上時，鋼軌波磨通過頻帶處的橫向蠕滑率峰值消失。

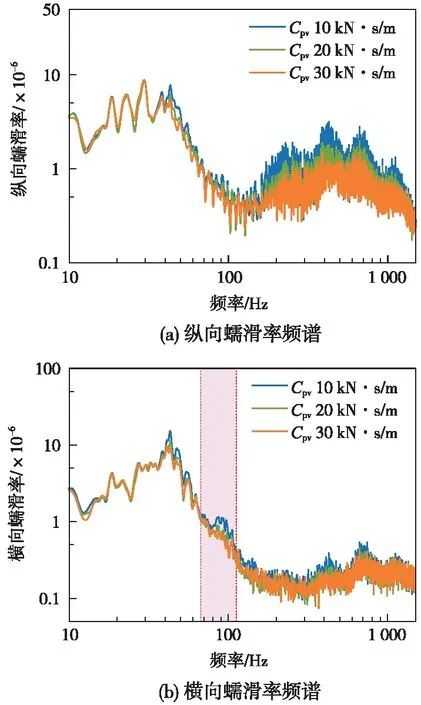
圖10 不同扣件垂向阻尼下蠕滑率頻譜

圖11為不同扣件垂向阻尼下的鋼軌磨耗功率頻譜圖。從圖11中可以看出，隨著扣件垂向阻尼的增大，不同頻段范圍內鋼軌磨耗功率有不同程度的衰減，以84，250，702 Hz和1 140 Hz處的磨耗功率衰減最為明顯。鋼軌波磨通過頻帶處的磨耗功率峰值在扣件垂向阻尼取值20 kN·s/m及以上時有消失趨勢，這是因為隨著扣件垂向阻尼增大，鋼軌波磨通過頻帶處橫向蠕滑率減小所致。250 Hz和702 Hz處磨耗功率隨著扣件垂向阻尼增大衰減較為明顯是因為隨著扣件垂向阻尼的增大，這兩處的橫向以及縱向蠕滑率減小所致，1 140 Hz處的磨耗功率衰減較為明顯是縱向蠕滑率隨著扣件垂向阻尼增大而減小所引起。因此可通過適當增大扣件垂向阻尼來減緩鋼軌波磨發展速率。

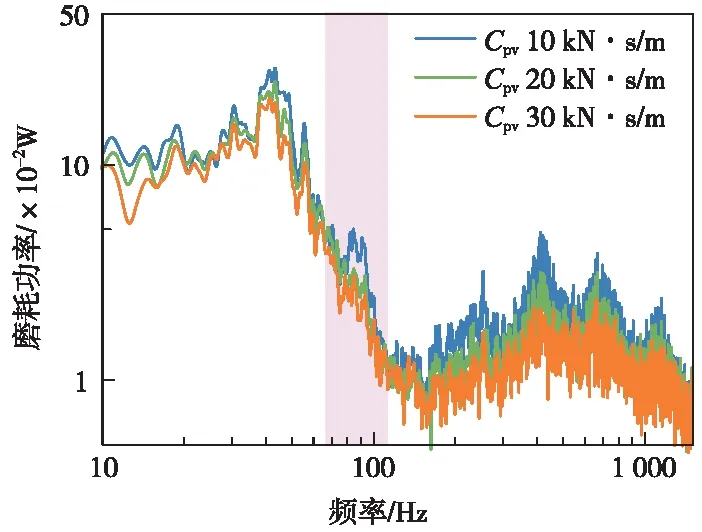
圖11 不同扣件垂向阻尼下鋼軌磨耗功率頻譜

5.4 扣件橫向剛度影響分析

本節扣件橫向剛度KpH分別取8.79，20，30 MN/m和40 MN/m，保持軌道系統其他參數不變，分析扣件橫向剛度的變化對輪軌接觸特性及鋼軌波磨發展特性的影響。

圖12(a)和圖12(b)分別為不同扣件垂向阻尼下的縱向蠕滑率和橫向蠕滑率頻譜圖，由圖12可知，扣件橫向剛度的變化對縱/橫向蠕滑率影響較小。

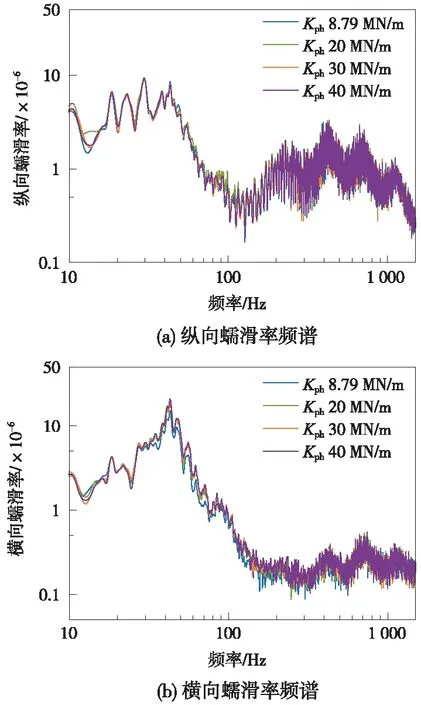
圖12 不同扣件橫向剛度下蠕滑率頻譜

圖13給出了不同扣件橫向剛度下的鋼軌磨耗功率計算結果。從圖中可以看出，扣件垂向剛度的變化對鋼軌磨耗功率影響較小，僅在鋼軌波磨通過頻帶處稍有影響。因此通過調整鋼軌扣件橫向剛度來抑制鋼軌波磨發展效果較弱。這是因為直線地段輪軌動態相互作用以輪軌垂向振動為主、輪軌橫向振動較弱導致。

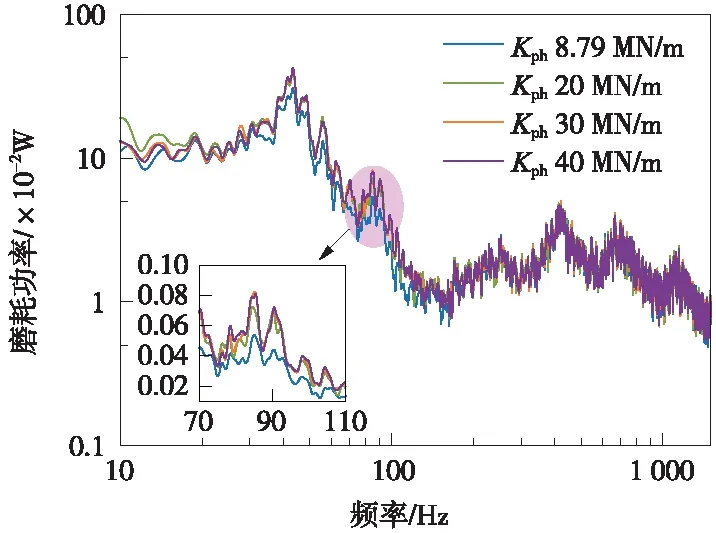
圖13 不同扣件橫向剛度下鋼軌磨耗功率頻譜

5.5 扣件橫向阻尼影響分析

本節扣件橫向阻尼CpH分別取10，20 kN·s/m和30 kN·s/m，保持軌道系統其他參數不變，分析扣件橫向阻尼的變化對輪軌接觸特性及鋼軌波磨發展特性的影響。

圖14(a)和圖14 (b)分別為不同扣件橫向阻尼下的縱向蠕滑率和橫向蠕滑率頻譜圖。由圖14(a)可知，扣件橫向阻尼的變化對縱向蠕滑率幾乎無影響；由圖14(b)可知，扣件橫向阻尼由10 kN·s/m增至20 kN·s/m時，橫向蠕滑率變化較小，扣件橫向阻尼由20 kN·s/m增至30 kN·s/m時，橫向蠕滑率在75～110 Hz處有小幅衰減。

圖14 不同扣件橫向阻尼下蠕滑率頻譜

圖15為不同扣件橫向阻尼下的鋼軌磨耗功率頻譜圖。由圖15可知，扣件橫向阻尼由10 kN·s/m增至20 kN·s/m時，鋼軌磨耗功率衰減現象不明顯；扣件橫向阻尼由20 kN·s/m增至30 kN·s/m時，磨耗功率在75～100 Hz處衰減現象較為明顯，衰減最大位置為85 Hz處。因此，本文建議扣件橫向阻尼取30 kN·s/m以上來減緩鋼軌波磨發展速率。

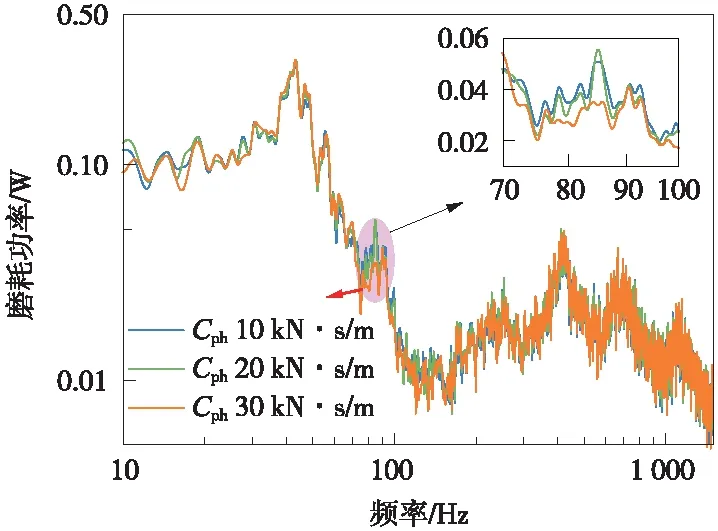
圖15 不同扣件橫向阻尼下鋼軌磨耗功率頻譜

6 結論

本文針對地鐵直線地段鋼彈簧浮置板軌道出現波長為160～250 mm的鋼軌波磨現象，基于有限元理論和車輛-軌道耦合動力學理論，建立了車輛-鋼彈簧浮置板軌道剛柔耦合動力學模型，從軌道系統振動特性和輪軌接觸特性角度出發，對鋼軌波磨形成原因及不同軌道結構參數下鋼軌波磨發展特性進行了分析，主要結論如下。

(1)鋼軌第10～14階橫向彎曲振動模態、軌道板第8～9階垂向彎曲振動模態和第6～8階扭轉振動模態是誘導鋼軌波磨產生的重要因素。

(2)直線地段鋼彈簧浮置板軌道特定波長鋼軌波磨的產生與鋼軌波磨通過頻帶處出現共振有關，鋼軌波磨通過頻帶處的共振現象導致該頻帶范圍內的輪軌橫向蠕滑率較為突出。

(3)在不影響行車安全性的前提下，通過適當將扣件垂向剛度控制在10～30 MN/m、將扣件垂/橫向阻尼控制在30 kN·s/m以上可抑制特定波長鋼軌波磨的發展。