考慮軸力作用下盾構下穿引起既有隧道變形解析解

喬曉延,齊曉強

(1.中交第二公路工程局有限公司,西安 710065； 2.青島理工大學土木工程學院,青島 266033)

引言

隨著城市化進程的不斷推進，城市地下空間發展已成為解決城市擁擠的一個重要途徑。城市新建地鐵線路很大程度上會對鄰近結構物產生應力應變響應，也不可避免地下穿鄰近既有運營線。對于如何合理評估隧道下穿既有線的影響已得到越來越多專家學者的青睞。

目前研究方法有實測分析[1-3]、有限元模擬[4-5]和室內實驗[6-7]方法，但理論解析的方法更為簡潔實用，可用來初步評估既有隧道在隧道下穿作用下的響應應答。該方法主要基于兩階段法，第一階段Loganathan等[8]提出的能夠估算隧道開挖引起周邊土體位移場變化的土體自由位移公式；第二階段將隧道簡化成梁單元，擱置在地基模型上獲得隧道變形控制方程；最后，解析方程獲得隧道變形及其內力應答。王海濤等[9]基于修正Winkler地基模型[10]，采用兩階段法和傅里葉級數的解法獲得新建隧道引起上覆管線變形矩陣解；李海麗等[11]基于Winkler地基模型和兩階段法，通過考慮土體模量對土與結構相互作用的影響獲得下穿隧道對上覆既有管線變形的解析解；LIU等[12]考慮土體反力是非線性關系，并基于Winkler地基模型獲得盾構下穿引起上方隧道變形解析解；梁榮柱等[13-14]用Euler-Bernoulli梁和Timoshenko梁模擬隧道單元，并將梁體擱置在Winkler地基模型上，分別獲得下穿隧道引起上覆隧道變形解析解和簡化計算方法；甘曉露等[15]采用兩階段法和Winkler地基模型，基于隧道開挖上浮效應獲得既有隧道在盾構下穿時變形半解析解。由于Winkler地基模型缺乏考慮土與結構相互作用中土體剪切影響，使得解析理論結果與實測數據有所差別。為克服這一缺點，Pasternak提出了Pasternak彈性地基模型[16]來預測土與結構相互作用的力學理論；林存剛等[17]基于Pasternak地基模型和Euler-Bernoulli梁理論，獲得下穿隧道引起上覆非連續性管線變形簡化計算方法；管凌霄等[18]基于Timoshenko梁和Pasternak地基模型，解析獲得隧道下穿引起上覆管線變形； LIANG等[19]引入非線性Pasternak地基模型，利用牛頓迭代法獲得了非線性土體下，上覆隧道在盾構下穿作用下的簡化計算方法；甘曉露等[20]基于Pasternak地基模型和兩階段法，獲得新建雙隧下穿施工引起上覆隧道沉降變形半解析解。綜上所述，下穿隧道施工引起既有隧道變形響應的解析方法大多數停留在單參數Winkler和雙參數Pasternak地基模型，較少有人考慮到精度更高的Kerr地基模型[21]，馮國輝等[22-23]與ZHANG等[24]均指出Kerr地基模型計算結果與實測數據吻合較好。

在已有研究基礎上提出了一種新簡化計算方法，采用Loganathan公式[8]獲得隧道開挖引起上覆隧道軸線處的土體自由位移，將土體自由位移附加在既有隧道上，將既有隧道簡化成無限長的Euler-Bernoulli梁擱置在三參數Kerr地基模型，并將既有隧道軸力納入考慮的范圍，結合兩階段法獲得隧道變形響應的簡化計算方法。通過與實測數據對比，本文方法計算結果較為符合；與本文方法退化解對比，本文方法的解析結果更具有優越性。隨后系統分析了地層損失率、新建隧道埋深、新建隧道直徑變化對既有隧道應力應變的影響。

1 分析過程

1.1 土體自由豎向位移場

1998年Loganathan提出盾構開挖引起鄰近土體自由位移場的表達式如下

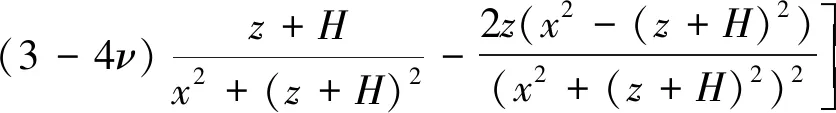
(1)

式中，R為隧道半徑；H為隧道軸線深度；x為既有隧道到開挖隧道中心線的水平距離；z為距地表垂直距離；ε為等效地層損失比；υ為土體泊松比。

考慮到實際工程大部分盾構隧道與鄰近隧道軸線不垂直的情況，如圖1所示，當隧道軸線與舊隧道軸線存在夾角α時，式(1)可修正為

S(x，z)=ε0R2×

(2)

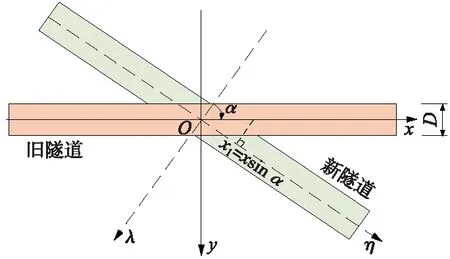
圖1 新舊隧道相交示意

1.2 既有隧道受力控制方程建立

如圖2所示，隧道與土體相互作用采用三參數Kerr地基模型，且隧道和周圍土體共同變形。假定盾構下穿引起上覆隧道的附加應力為q，由Kerr地基模型特性可知，在該附加應力作用下既有隧道豎向撓度為

w=w1+w2

(3)

式中，w1為上層彈簧的變形量；w2為剪切層變形量。假設既有隧道及剪切層下側的應力分別為

p1=cw1=c(w-w2)

(4)

p2=kw2

(5)

式中，c為上層彈簧剛度；k為下層彈簧剛度。對于剪切層[16]，有

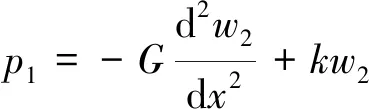
(6)

式中，G為剪切層剛度。通過式(4)、式(6)，可以得到

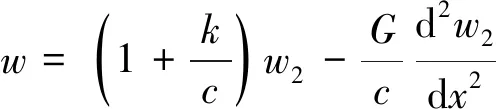
(7)

將隧道簡化成無限長的Euler-Bernoulli梁擱置在Kerr地基模型上，并將隧道二階軸力效應納入考慮的范圍，可獲得其微元段豎向力平衡控制方程為

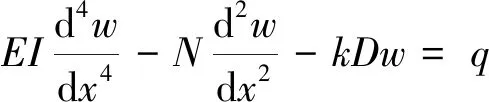
(8)

式中，w為隧道位移；EI為既有隧道抗彎剛度；N為軸向壓力；D為隧道直徑；q為隧道受到的附加應力，其大小為

q=cS(x，z)

(9)

式中，c為Kerr地基模型上層彈簧剛度；S(x，z)可由式(2)得到，其中，z為既有隧道軸線埋深。

結合式(7)、式(8)可知

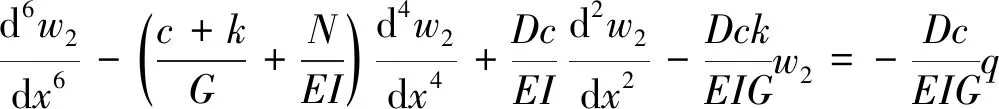
(10)

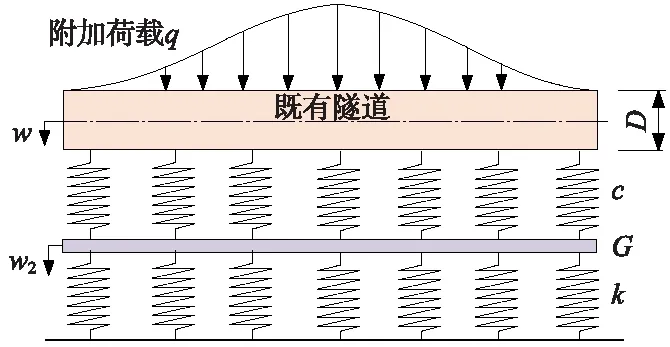
圖2 Kerr地基下隧土相互作用模型

1.3 Kerr地基模型參數確定

Kerr地基模型參數的確定對于計算結果的正確性起到關鍵作用，根據簡化彈性空間法可得

c=3k，k=4Es/3z，G=2Esz/9(1+ν)

(11)

式中，Es和ν分別為土體彈性模量和泊松比；z為既有隧道軸線埋置深度。然而，簡化彈性空間法雖然操作簡便，但由于引入較多假設，此時會造成計算精度并不高，故需調整各個參數的取值來滿足實測要求。為得到更精確的計算結果，馮國輝等[23]提出了基于有限元方法驗證得到的修正地基基床系數，即

c=7k，k=4Es/3z，G=2Esz/9(1+ν)

(12)

1.4 控制方程的求解

式(10)為6階微分方程，由于其較難獲得解析解，采用差分解獲得其數值解。將既有隧道離散為m+7個點(其中兩端存在6個虛點)，相鄰虛點之間間距為l，且l=L/m，其中，L為既有隧道長度。隧道離散化如圖3所示。

圖3 既有隧道離散

此時，式(10)可簡化成

t(6)+χ1t(4)+χ2t(2)+χ3t=χ4

(13)

式中，t(n)為w2的n階導數；χ1、χ2、χ3、χ4分別為

(14)

根據實際兩端邊界條件進行簡化，無限長隧道兩端受下穿隧道開挖的影響很小，可將既有隧道兩端簡化成兩個自由端，這樣便可消去隧道兩端6個虛擬單元，其矩陣形式為

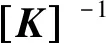
(15)

式中{t}，[F]表示如下

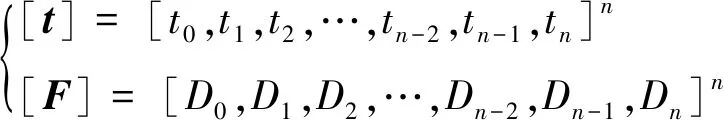
(16)

[K]可表示為

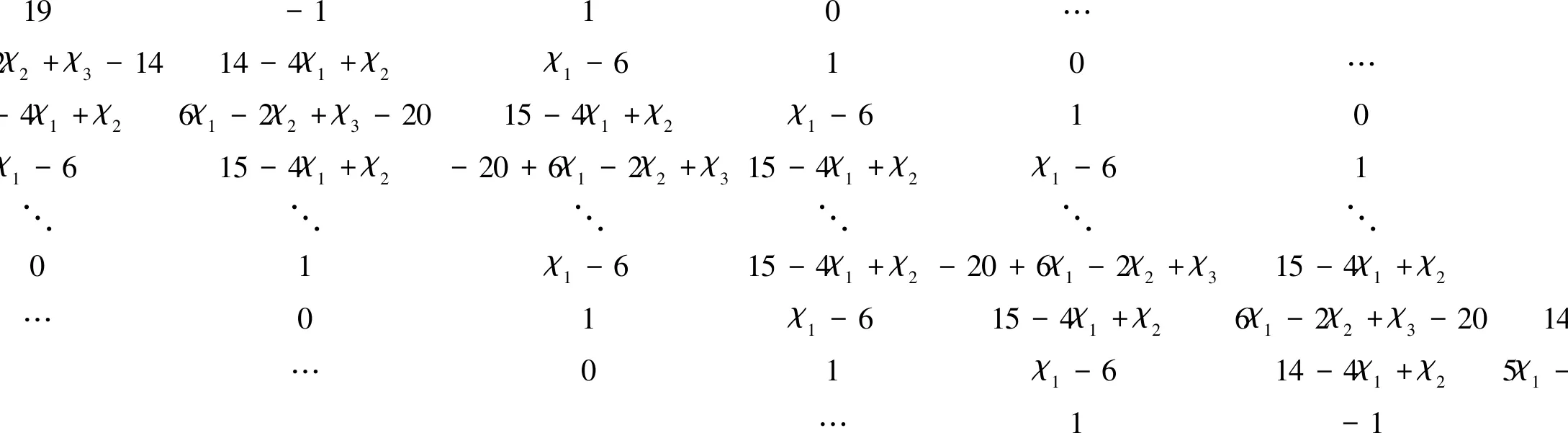
(17)

此時，得到為w2(x)位移的半解析解，通過式(7)即可得到隧道縱向位移w(x)。同時，也可得到隧道彎矩和剪力如下

(18)

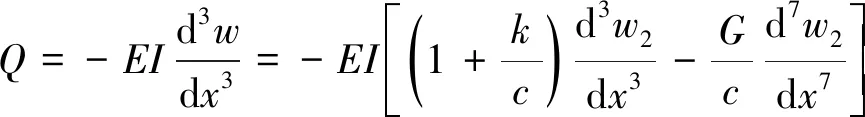
(19)

值得注意的是，當隧道軸力N=0時，本文解析將退化成只有附加應力作用下的既有隧道變形響應(EB-K模型)。當軸力N=0且Kerr地基模型中參數c=0時，隧道-土之間相互作用將退化成Pasternak地基模型(EB-P模型)。

2 算例驗證

2.1 工程概況

JIN等[1]曾報道過深圳地鐵9號線雙線隧道下穿既有4號線隧道的工程案例。取9號線左線下穿既有隧道的實測數據與本文方法計算結果進行對比。如圖4所示，新建隧道與既有隧道埋深分別為H=20.5 m和z=12.0 m，兩隧道軸線夾角為α=83°，兩隧道外徑均為6 m，襯砌厚度為30 cm。由文獻[20]可知，既有隧道抗彎模量為EI=1.17×108kN·m，新建隧道引起的地層損失率為ε=0.5%。其土體彈性模量為Es=62.5 MPa[20]，土體泊松比υ=0.3。考慮到既有隧道軸力的影響，根據文獻[2]，可取既有隧道管片間拼裝軸力為80 MN。

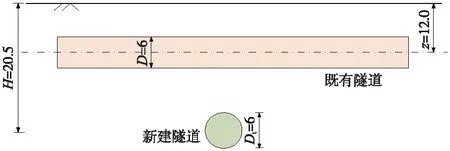
圖4 兩隧之間相對位置簡化(單位：m)

2.2 計算結果分析與比較

圖5為本文計算結果與工程監測數據的對比，其監測數據來自文獻[1]。由圖5可見，本文方法和本文方法退化解(EB-K模型和EB-P模型)與監測數據結果趨勢一致。既有隧道豎向變形主要發生在距離隧道中軸線兩側40 m范圍內，與監測數據分布規律相符合。采用本文方法計算得到隧道沉降位移為5.4 mm；本文退化EB-K模型(即不考慮本文提出的側向土體作用時)計算結果稍微較大，其位移峰值為5.8 mm；EB-P模型(即將既有隧道簡化成Euler-Bernoulli梁擱置在Pasternak地基模型上)計算結果明顯偏大，隧道最大位移為7.1 mm。造成這一現象的原因在于本文提出的既有隧道軸力作用，使得隧道縱向長度上管片更加緊密，既有隧道抵抗變形的能力增強，顯然會減小隧道沉降；此外，Pasternak地基模型未考慮多參數對隧道位移預測結果的影響，其計算數值也會偏大。與本文方法的退化解相比較，監測數據最大隧道位移為5.3 mm[1]，明顯本文方法計算結果更加符合監測數據。在同等條件下，本文方法可作為一種快速評價盾構下穿對既有隧道影響的工具，對實際工程具有一定指導意義。

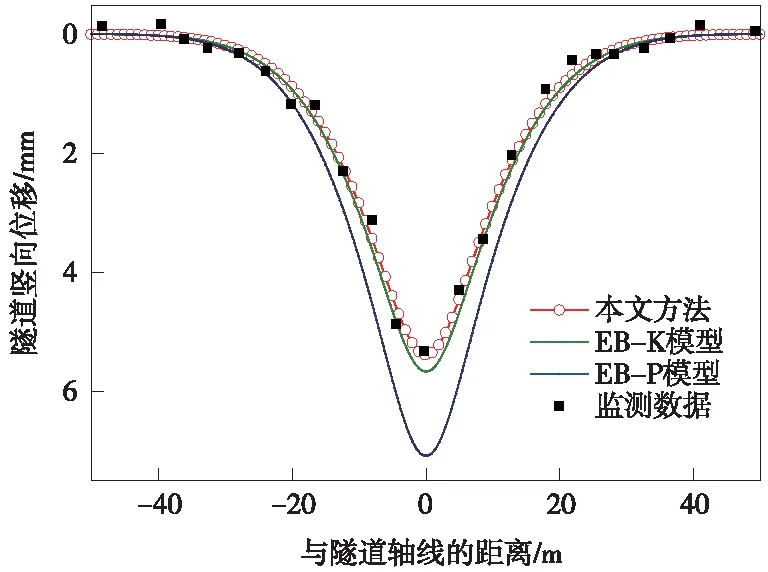
圖5 隧道縱向計算、有限元及監測數據對比曲線

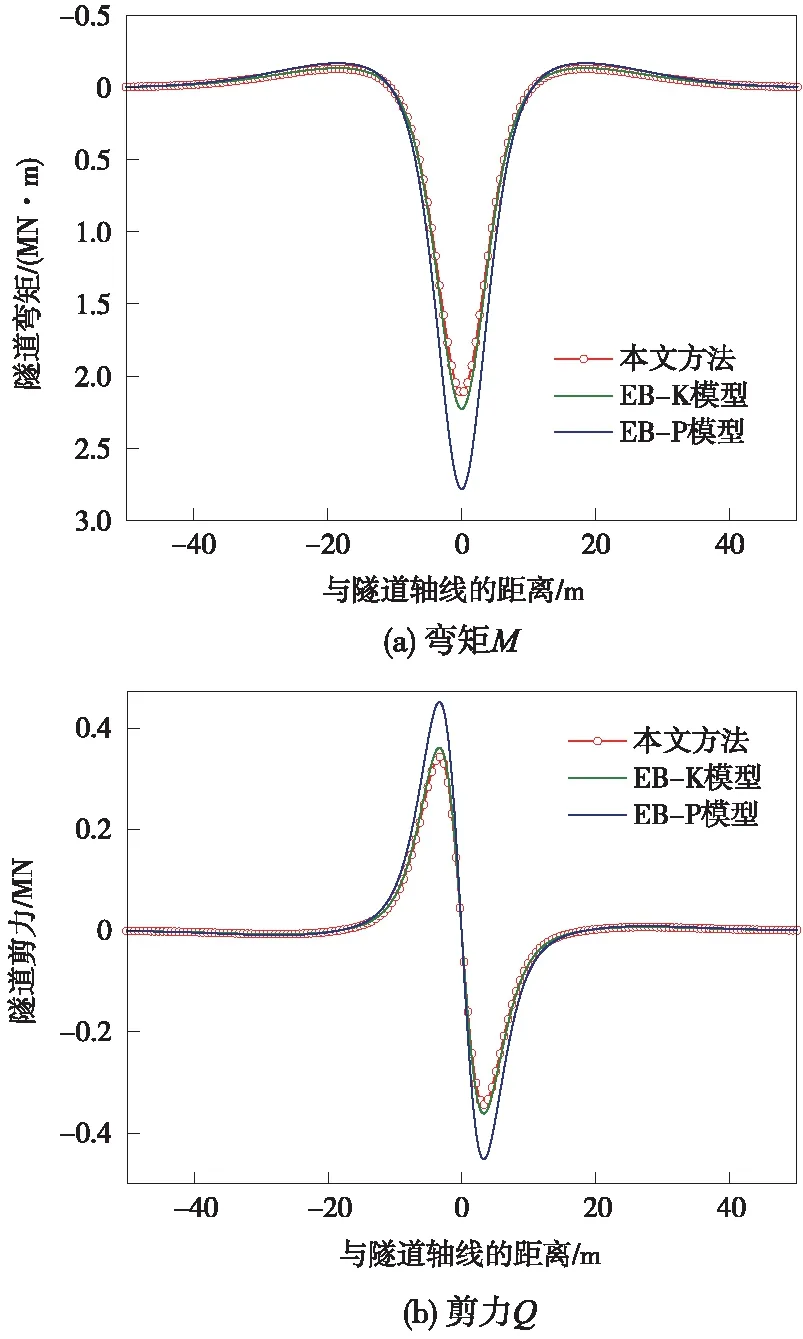
圖6 隧道縱向內力分布對比曲線

圖6為本文方法及其退化解計算得到的既有隧道縱向彎矩和剪力對比曲線。由圖6可知，本文方法計算結果與本文退化解EB-K計算結果相近，但本文方法結果偏小，而EB-P模型計算結果明顯偏大，這和Pasternak地基模型預測隧道變形步調一致，由于未能考慮到多參數因素對土與結構相互作用的影響。因此，本文方法及EB-K模型在預測土與結構相互作用時有很大優勢，進一步說明本文方法的合理性。

此外，由圖6還可以看出：隧道彎矩變化曲線沿隧道中心軸線成正對稱分布，最大正彎矩(隧道下側受拉)位于隧道中心點處，明顯大于隧道最大負彎矩值；隧道剪力變化曲線沿隧道中心點成中心對稱分布，最大剪力出現在離隧道中心點處4 m處。這些內力峰值出現的位置均為危險截面，在實際工程中需予以重視。

3 參數分析

為研究隧道應力應變與關鍵工程參數的關系，建立如下工程案例：既有隧道和開挖隧道直徑均為D=D0=6 m，既有隧道和開挖隧道軸線埋深分別為z=10 m和H=20 m，土體泊松比為υ=0.3，新舊隧道平面夾角為α=90°，土體模量Es=60 MPa，既有隧道抗彎剛度為EI=1.17×108kN·m，新建隧道造成地層損失率為ε=1%。

3.1 地層損失率影響

圖7、圖8分別為不同地層損失率下對既有隧道縱向位移及彎矩影響曲線。由圖7、圖8可以看出，隧道縱向位移和彎矩變化曲線沿隧道軸線對稱分布，當距離隧道中心線為0時，隧道縱向位移變形量和彎矩值最大；隨著地層損失率增大，隧道縱向位移量和彎矩均會隨之增大，說明地層損失率越大，盾構下穿既有隧道就越危險；同時，隨著地層損失率的線性增大，隧道變形位移及其彎矩也會出現線性增大；筆者認為由于隨著地層損失率的增大，既有隧道軸線處受到的附加應力呈線性增大，致使隧道每個位置處的下沉位移會與地層損失率線性相關。還可以看出，隧道中軸線的位移峰值和彎矩峰值最大的，因此，在實際工程中，應盡可能地減小盾構開挖對周邊土體的擾動以減小地層損失率，從而從根本上保證既有隧道安全。

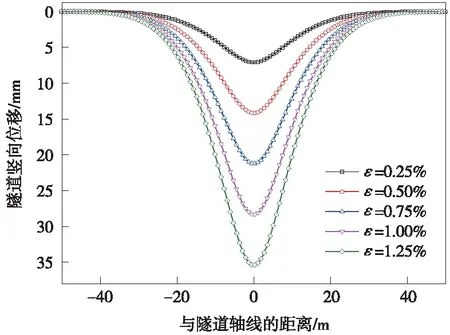
圖7 不同地層損失率下隧道位移曲線

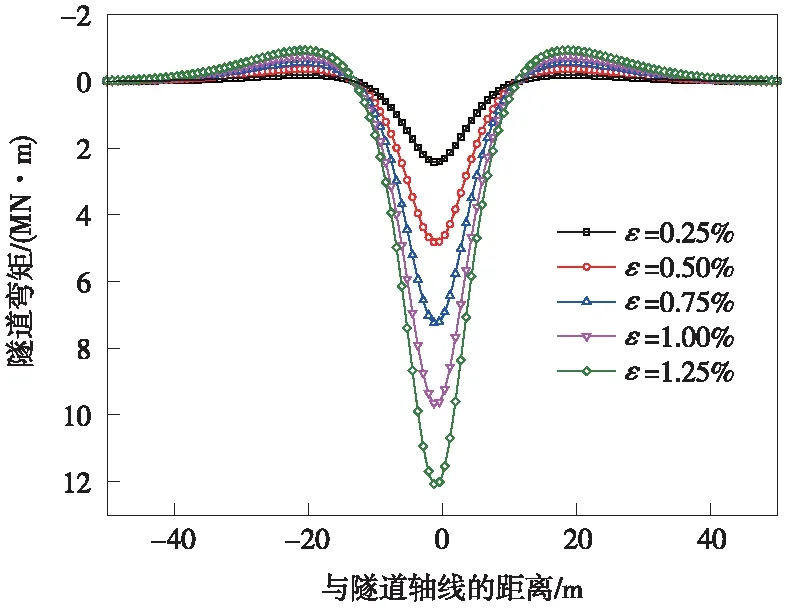
圖8 不同地層損失率下隧道彎矩曲線

3.2 新建隧道軸線埋深影響

圖9為不同隧道軸線埋深下隧道縱向最大位移wmax和最大彎矩Mmax變化曲線。由圖9可以看出，新建隧道埋深由18 m增加至28 m過程中，既有隧道縱向位移從15.6 mm逐漸減小到10.3 mm，降幅接近34%，減小速率基本不變。還可以看出，增大新建隧道埋深時，隧道彎矩從6.7 MN·m逐漸減小至2.0 MN·m，彎矩降幅接近70%。隨著新建隧道埋深增加，盾構開挖引起既有隧道軸線處的附加應力在土層中逐漸消散，導致隧道縱向位移變形及彎矩均大幅度減小。相比于隧道縱向位移變化，隧道彎矩變化更為敏感，但總的來說，新建隧道埋深變化是引起既有隧道受力變形的敏感參數，這對于指導實際工程具有一定意義，實際工程中可盡可能增加盾構開挖深度來降低對上覆既有隧道的影響。

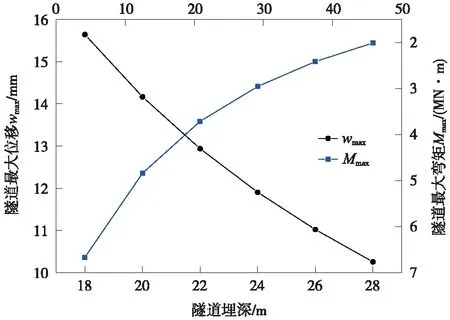
圖9 不同新建隧道軸線埋深下隧道最大位移和彎矩變化曲線

3.3 新建隧道直徑影響

圖10為不同隧道軸線埋深下隧道縱向最大位移wmax和最大剪力Qmax變化曲線。由圖10可以看出，隨著新建隧道直徑增大，既有隧道縱向位移從14.6 mm逐漸增大到47.7 mm，增幅高達2.27倍，增速基本不變。還可以看出，新建隧道直徑從6 m增加至11 m過程中，隧道剪力從0.61 MN逐漸增加至1.91 MN，剪力增幅高達2.13倍，增速基本不變。隨著新建隧道開挖直徑增大，盾構開挖引起既有隧道軸線處的附加應力也會逐漸增大，導致既有隧道縱向位移變形及剪力均大幅度增大，說明新建隧道開挖直徑變化是引起既有隧道受力變形的敏感參數，在實際工程中可通過減小盾構開挖直徑來保護既有上覆隧道應力應變的安全性。

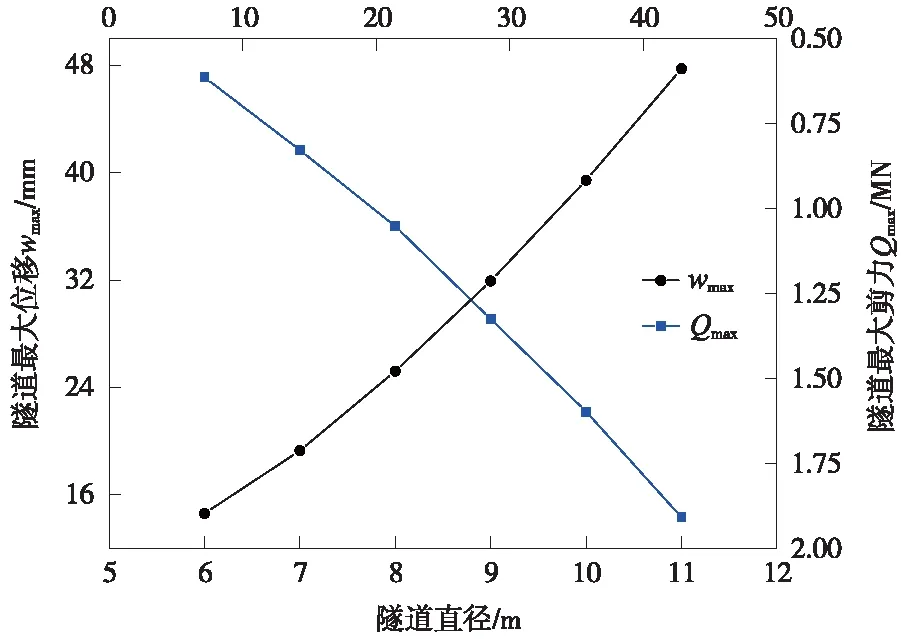
圖10 不同新建隧道直徑下隧道最大位移和剪力變化曲線

4 結論

(1)基于兩階段方法，采用Loganathan公式獲得盾構下穿引起鄰近土體自由位移，將土體自由位移施加在既有隧道上，土與結構相互作用采用三參數Kerr地基模型，引入軸力對既有隧道的影響因素獲得既有隧道沉降變形解析。

(2)將收集到既有文獻中的實測數據與本文計算方法結果對比，驗證了本文方法的有效性；相比于本文方法可退化的EB-K模型和EB-P模型，本文方法更具有優越性。

(3)對盾構開挖下穿引起既有隧道受力變形不同影響因素的研究結果表明：地層損失率增大會使得既有隧道位移及其內力線性增大；開挖隧道埋深增大會引起既有隧道位移和內力減小；增大開挖隧道直徑會顯著增大既有隧道的變形及其內力。