兩邊連接豎放波折鋼板墻內嵌墻板抗側性能及優化設計

竇 超，謝志棟，楊 娜

(1. 北京交通大學土木建筑工程學院，北京 100044；2. 結構風工程與城市風環境北京市重點實驗室，北京 100044)

鋼板剪力墻結構體系符合雙重抗震防線、延性好、耗能能力強等抗震設計要求，應用到許多高層及超高層建筑中，且近些年來出現了各種新的改進形式[1?4]。對于四邊連接平鋼板剪力墻結構國內外學者進行了大量的試驗和理論分析[5?10]，形成了較為成熟的計算理論和設計方法。但研究同時發現，由于內嵌平鋼板極易屈曲，形成的拉力帶對框架柱產生較大的附加彎矩作用。為了避免拉力帶對邊緣框架的不利影響及門窗開洞的需要，XUE 和LU[8]提出了兩邊連接平鋼板剪力墻，即內嵌墻板僅與框架梁相連、不與框架柱連接。雖然此類墻板改善了框架柱的受力，但由于缺少邊緣構件的約束，墻板拉力帶不能充分發展，其剛度和承載力受到較大削弱。

相比平鋼板剪力墻，波折鋼板墻中波折大大提高了墻板的面外剛度和抗剪屈曲荷載。合理設計時具有受剪屈服的抗側機理，對邊緣框架的錨固剛度要求以及附加彎矩的不利影響顯著降低，同時滯回曲線飽滿，耗能能力有顯著提高[11?18]。對于四邊連接波折鋼板剪力墻已有很多學者開展了研究。EMAMI 等[11? 12]進行了波折鋼板墻滯回試驗及數值對比分析。結果表明，盡管發生剪切屈曲后墻板承載力會突然下降，但隨即又逐步上升，并沒有持續喪失承載力。KALALI 等[13]研究了波形鋼板墻的單向推覆性能及滯回性能，指出合理選擇波形鋼板墻的板厚及波折尺寸時，能夠獲得比平鋼板墻更優越的受力性能。ZHAO 等[14]的數值參數化分析發現，相比平鋼板墻，波形鋼板墻具有更好的抗震性能，并對周邊框架的需求降低。DOU 等[16]提出了波折墻板的抗側承載力公式，指出部分墻板存在屈曲或屈服后抗側承載力顯著下降的問題，延性是波折墻板設計中的一個重要指標。TONG 等[17? 18]對加勁波折鋼板墻以及雙層波折內嵌墻板的抗剪承載力進行了數值分析研究，提出了達到充分加勁效果的加勁構件剛度取值和極限承載力計算方法。FENG 等[19]通過理論推導得到了板帶加勁波折墻板的屈曲荷載。ROUDSARI 等[20]通過數值分析研究了墻板開洞對波形鋼板剪力墻的剛度、承載力和延性的影響。王威等[21]通過對4 片波形鋼板墻及其與混凝土板組合墻體的低周往復加載試驗并結合有限元研究，揭示了豎放波形鋼板應用于組合墻體中可以提高其承載性能。DENG 等[22]提出了波形鋼板剪力墻多高層整體結構的一種高效數值計算模型，可用來進行地震模擬分析。BROUJERDIAN 等[23]提出了一種平鋼板和波折鋼板通過螺栓連接形成的組合截面鋼板墻，并對其抗側性能進行了參數化數值分析。

由于波折墻板可看作正交異性板，其兩個方向的面外抗彎剛度存在巨大差異，這就導致對于豎放波折墻板兩側邊柱的約束對其性能影響很小，而上下框架梁的約束作用更大。利用這一特點，豎向放置的波折墻板更適合用于兩邊連接剪力墻中[24?28]。目前對于兩邊連接波折鋼板墻以及加勁鋼板墻，魏瑤等[24]討論了加勁三角形波折墻板的彈性屈曲性能；趙秋紅等[25]對豎放波折鋼板墻的抗側性能開展研究，指出受自由邊影響其承載力下降約16%。FANG 等[26]對半剛性框架—兩邊連接豎放波折墻板開展了試驗研究，并提出了屈服荷載及極限承載力的計算公式，但并未討論墻板的選型及延性設計。

可以看到，已有研究主要集中在四邊連接波折鋼板剪力墻，而兩邊連接波折鋼板墻的研究較少。一方面，大多數研究僅關注波折墻板最大抗側承載力，而忽視了墻板屈曲后的承載力和延性性能[11?14]，但屈曲后性能對抗震設計又是尤為重要；另一方面，相比平鋼板墻，波折鋼板墻的幾何參數更多、抗側機理更為復雜，目前研究只是給出了墻板參數對抗側或滯回性能的影響規律，至于這些關鍵參數在設計中如何取值，并未給出定量的明確的建議[17?18]。因此，設計人員在波折鋼板剪力墻的初步設計時，如何進行內嵌波折墻板的選型即定量地選取墻板的各個幾何參數，尚沒有研究成果可供借鑒。在這種情況下，其不得不借助復雜的有限元軟件來建模進行不斷分析嘗試，才能確定合理的墻板選型，這無疑為初步設計帶來了巨大的困難，制約著波折鋼板墻的推廣應用。

針對上述問題，本文在對有限元分析模型進行充分驗證的基礎上，對兩邊連接豎放波折墻板的抗側性能及優化選型進行數值分析研究，揭示墻板的抗側機制及關鍵幾何參數對抗側性能的影響；在墻板兩側邊設置加勁構件，提出側邊加勁構件的選型和剛度設計建議；最后，闡明了波折墻板在往復荷載下和單向推覆下的抗側性能差異，并在往復荷載作用下提出了兩邊連接加勁豎放波折墻板的優化選型取值表，為墻板的初步設計提供了重要參考。

1 有限元模型及驗證

由于本文研究目的在于重點考察內嵌墻板的抗側性能(而不考慮框架作用)，因此如圖1 所示采用單層單跨鉸接剛性框架—波折墻板的分析模型進行單向推覆和往復加載分析。內嵌波折墻板豎向放置，僅與框架梁剛性相連。之所以采用無限剛性的梁柱鉸接框架，是為了保證內嵌墻板單獨承擔水平剪力，不考慮框架的抗側貢獻。

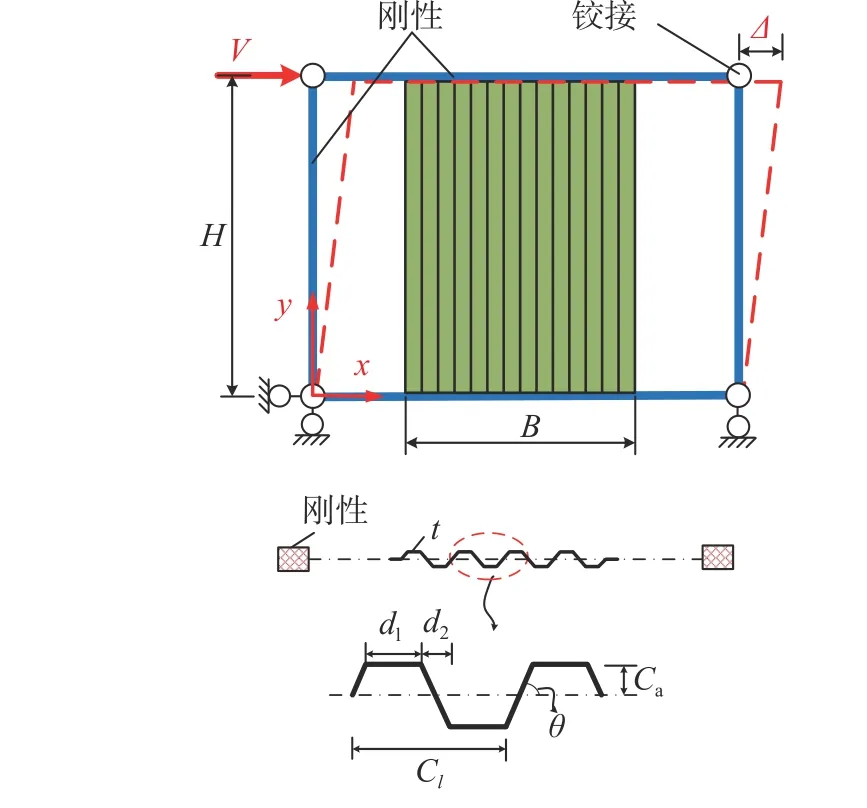
圖1 鉸接剛性框架模型Fig. 1 Hinged rigid frame model

在有限元軟件ABAQUS 中建立上述模型，所有構件均采用S4R 殼單元進行模擬。波折墻板采用雙折線彈塑性模型的Q235 鋼材，屈服強度fy=235 MPa，彈性模量E=206 GPa，切線模量Et=0.01E，泊松比ν=0.3。采用von Mises 屈服準則和隨動強化理論，以考慮包辛格效應的影響。邊緣框架的彈性模量取為100E來實現剛性框架。約束框架底梁全部自由度，通過耦合梁柱連接節點的平動位移實現鉸接框架。在上梁端部加載點采用位移控制方式進行加載。考慮樓板對框架梁的面外約束，限制梁翼緣的面外側移。采用靜力隱式算法進行單向推覆和往復加載分析。采用一致缺陷法施加墻板的初始幾何缺陷，即缺陷與第一階屈曲模態一致，幅值為1/750H。為了準確描述波折墻板的受力和變形，每一個波折子板面沿波長方向劃分4 個單元[27]，同時單元寬高比小于1.5。

為了證明本文采用的有限元數值模型及分析方法能夠有效地進行波折鋼板墻結構的抗側性能分析計算，必須將其與現有試驗結果進行對比。這里分別選取文獻[11]和文獻[15]的四邊連接波折鋼板墻往復加載試驗進行模擬對比分析。對于文獻[11]中的試件3，根據試驗實際尺寸、材性實驗參數及邊界條件建立模型(圖2(a))，其中，墻板高為H=1500 mm，寬為B=2000 mm，厚度為t=1.5 mm。圖2(b)給出了有限元分析結果與試驗結果的對比。有限元得到滯回曲線包絡面積比試驗稍大，總體能夠獲得與試驗吻合的極限承載力。

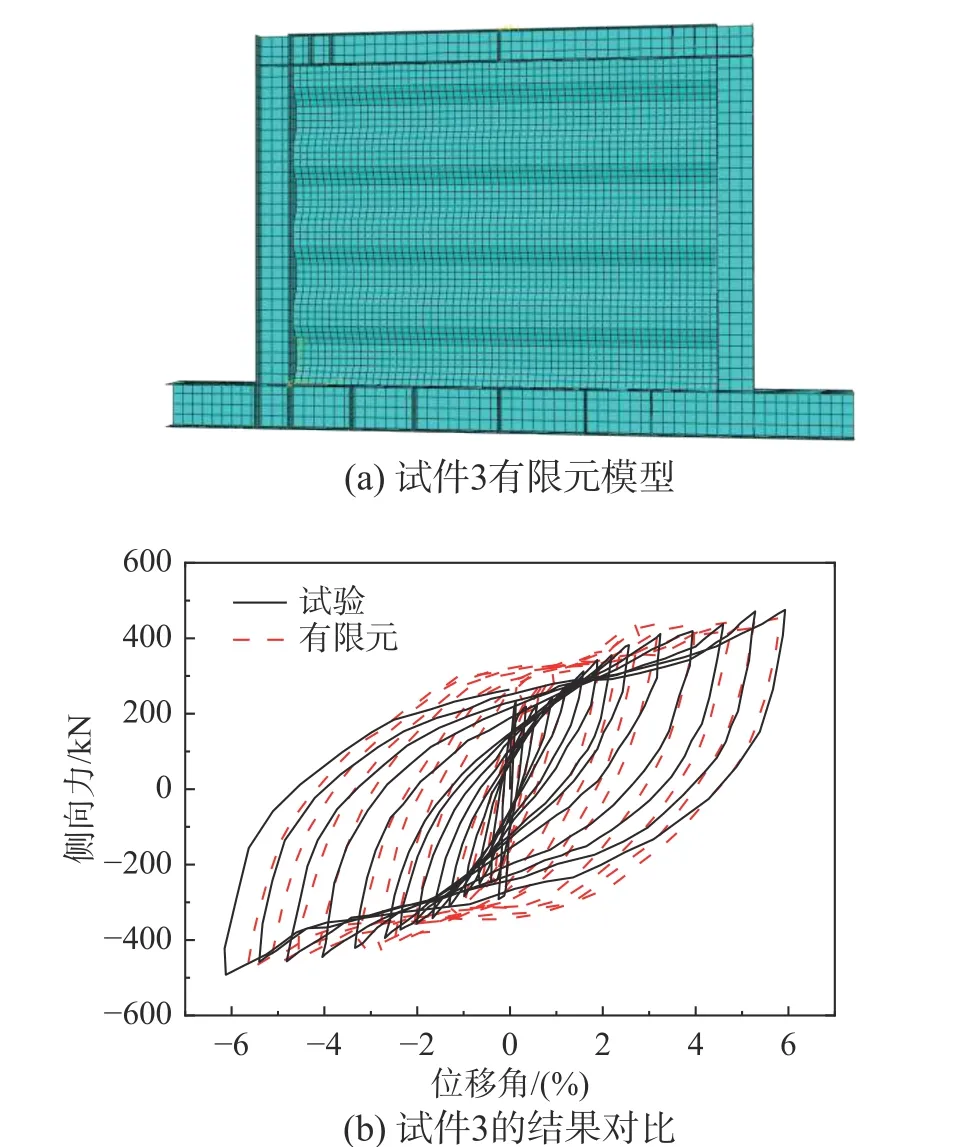
圖2 有限元與文獻[11]的試驗結果對比Fig. 2 Comparison of FEA and test results in Ref. [11]

文獻[15]對單跨兩層波折鋼板墻進行了往復加載試驗。選取試件HCoSPSW-Ⅰ進行建模分析，內嵌墻板尺寸為H×B×t=1100 mm×1100 mm×2 mm，有限元模擬結果與試驗結果的對比如圖3所示。可以看到，當層間位移角1.0%時，極限承載力的有限元結果為618 kN，試驗結果為610 kN；達到最大層間位移角時，二者分別為538 kN 和514 kN。對比結果表明，有限元數值分析不僅能夠準確地得到鋼板墻的極限承載力，且能獲得較為真實的強度退化規律即屈曲后性能。

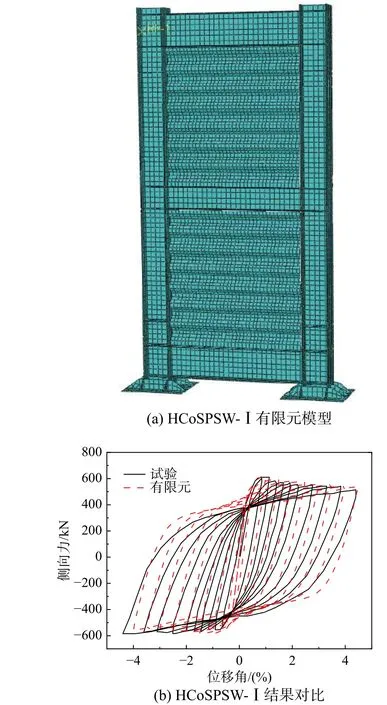
圖3 有限元與文獻[15]的試驗結果對比Fig. 3 Comparison of FEA and test results in Ref. [15]

此外，對于兩邊連接豎放波折鋼板墻，文獻[28]開展了滯回性能試驗研究。如圖4(a)所示，試件S-3的開洞率為33%，墻板尺寸為H×B×t=1000 mm×1200 mm×3 mm，左右兩側邊設置有100 mm×10 mm的平板加勁肋條。同理，采用文獻[28]中的相同尺寸及材料、邊界參數建立有限元模型(圖4(a))進行往復加載分析，滯回曲線如圖4(b)所示，與試驗結果吻合較好，極限承載力比試驗值低約4.6%，最大層間角時的承載力比試驗值高約7.0%。

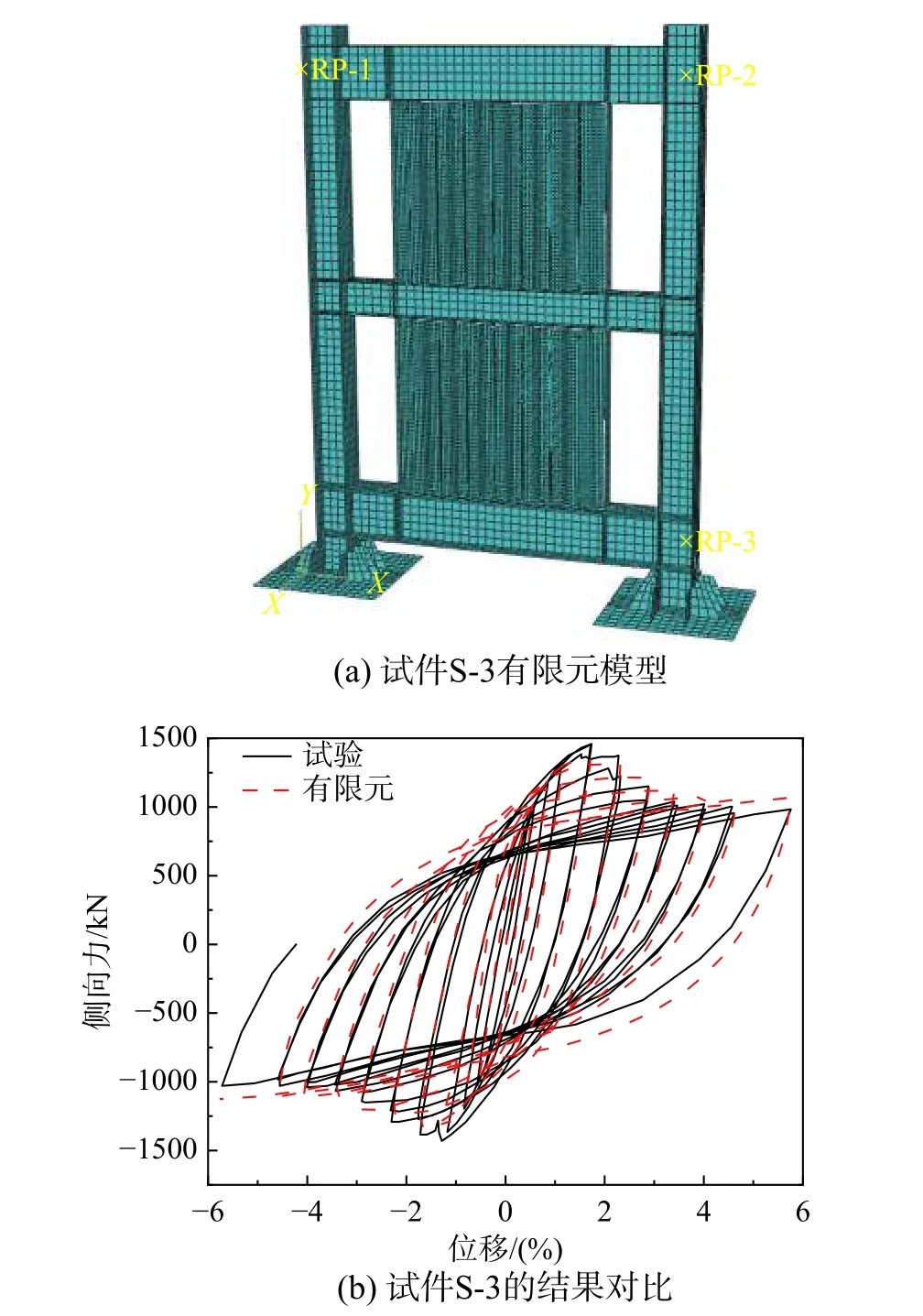
圖4 有限元與文獻[28]的試驗結果對比Fig. 4 Comparison of FEA and test results in Ref. [28]

綜上，本文采用ABAQUS 對波折鋼板墻的建模和分析方法具有可行性，分析結果可靠，可以基于數值結果提出相應設計方法和建議。

為了更加直接地比較不同參數對內嵌波折墻板的影響，將墻板承載力進行歸一化。定義內嵌墻板的最大承載力為極限承載力Vs，與大震層間位移角限值2.0%所對應的承載力稱為殘余承載力Vr，對應的歸一化極限承載力系數φs和殘余承載力系數φr分別為：

2 豎放波折墻板的抗側曲線

Vy為墻板全截面剪切屈服承載力：

式中：τy為鋼材剪切屈服強度；B和t分別為墻板的寬度和厚度(圖1)。

上述兩個承載力系數直接反映了墻板的承載效率，其越接近1.0 表明墻板以抗剪屈服機制為主，越接近面內抗剪受力狀態，材料利用率越高。此外，殘余承載力系數與極限承載力系數的比值φr/φs可用來評估墻板屈曲后承載性能，其值越大表明屈曲后承載力越穩定。

波折內嵌墻板的幾何參數不同，其抗側承載力曲線將會有顯著差異，主要反映在屈曲后承載力及延性性能。選取兩個典型算例，其幾何參數及抗側曲線如圖5 所示。相比于第一類較為穩定的抗側承載力，第二類曲線在極值點后出現迅速下降，表現出極不穩定的屈曲后承載能力，導致墻板的延性性能較差。因此在設計中，應通過波折墻板的優化選型，避免第二類情況出現。

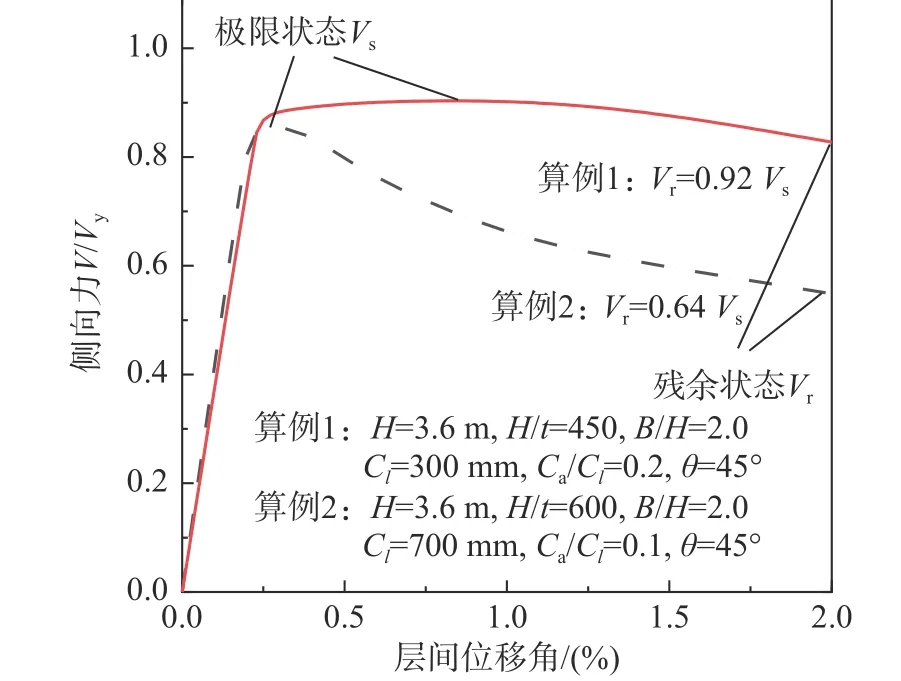
圖5 典型波折鋼板的荷載-位移曲線Fig. 5 Load-displacement curves of typical corrugated steel plates

定義對應于上述兩類曲線的墻板分別為“強墻板”和“弱墻板”，具體量化指標為：弱墻板殘余承載力系數與極限承載力系數的比值φr/φs<0.85，意味著屈曲后承載力下降明顯；而強墻板的φr/φs≥0.85，也就是說到達最大層間位移角時仍保持足夠延性。

圖6 所示為強墻板(算例1)和弱墻板(算例2)在最大層間位移角下的等效應力圖，陰影區域代表材料屈服。可以看到，強墻板的屈服面積明顯要比弱墻板的屈服面積大。強墻板能夠實現平面內受剪從而接近于全截面屈服，而弱墻板部分截面并沒有達到屈服。

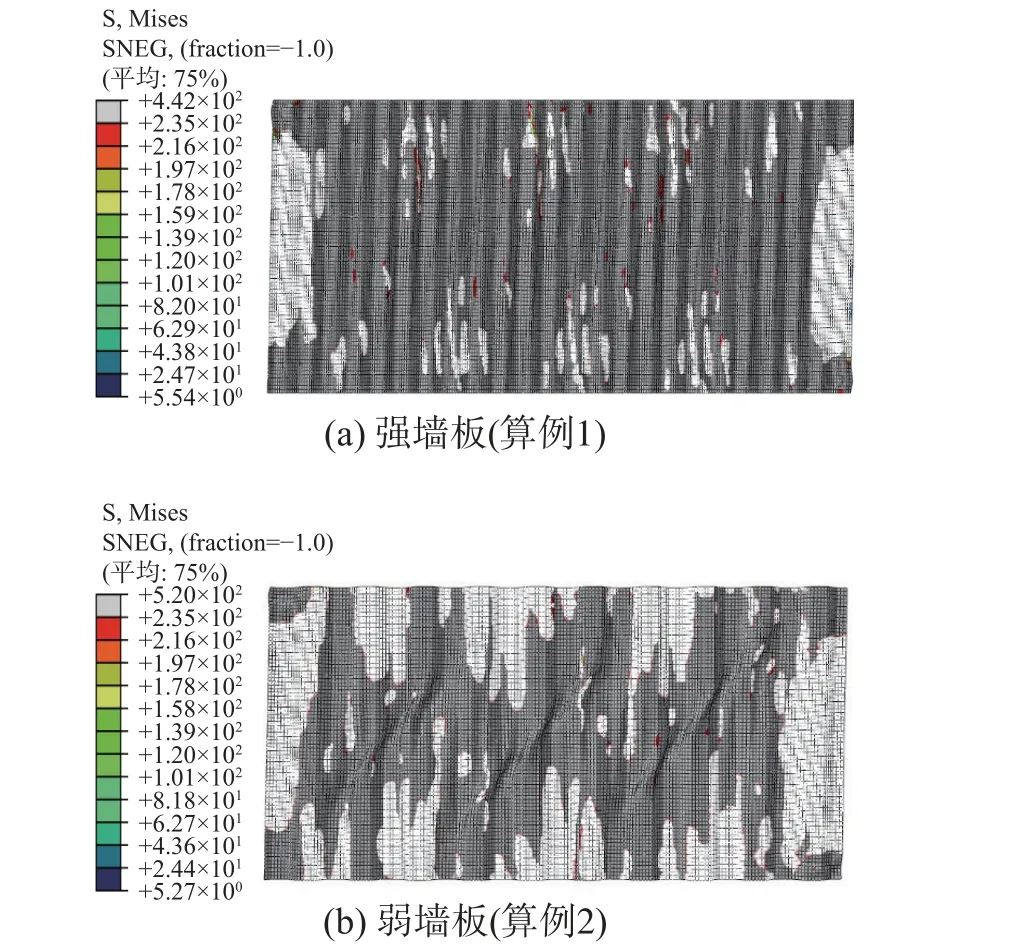
圖6 典型波折鋼板的等效應力圖(層間位移角2%)Fig. 6 Equivalent stress diagram of typical corrugated steel plate (drift ratio 2%)

強墻板和弱墻板在殘余狀態下的面外變形模式不同(圖7)，強墻板的面外變形為橫跨幾個波折的整體變形，最大面外變形為70 mm；而弱墻板的面外變形為橫跨幾個波折的“拉力帶”變形，最大面外變形為93 mm。墻板面外變形的不同，導致墻板的抗側機制發生不同。

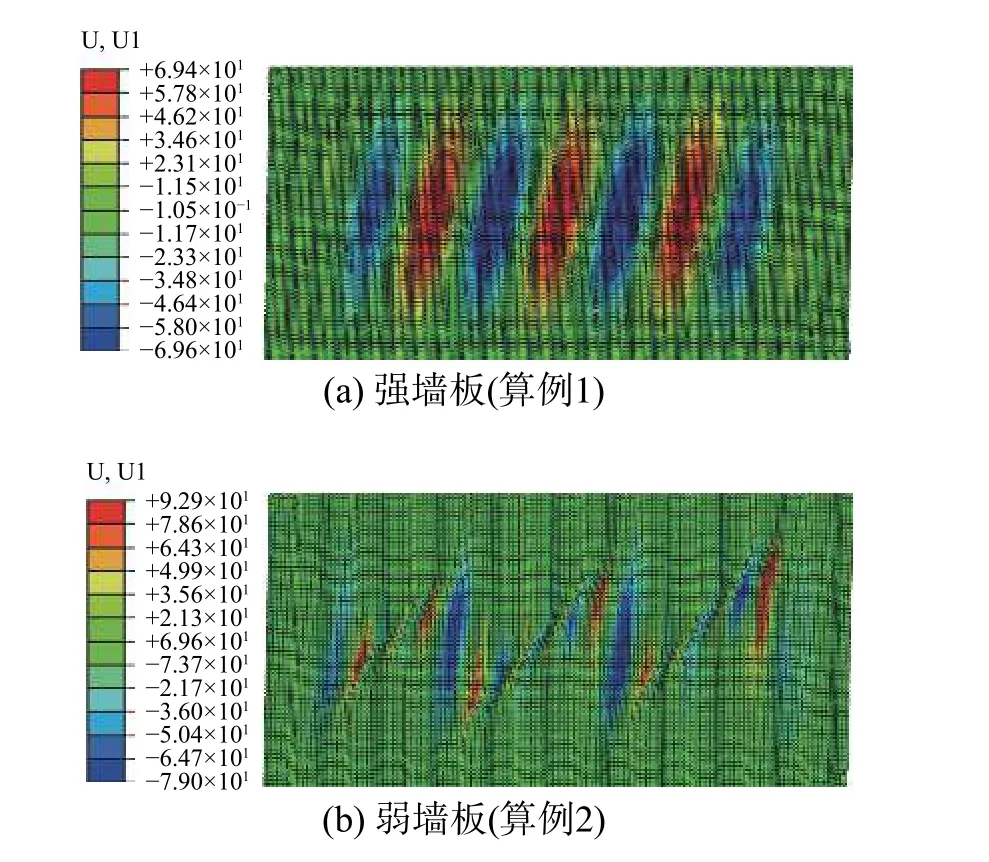
圖7 典型波折鋼板的面外變形(層間位移角2%)Fig. 7 Out-of-plane deformation of typical corrugated steel plate (drift ratio 2%)

3 幾何參數對墻板抗側性能影響

兩邊連接豎放波折墻板在設計時，需要6 個幾何參數才能確定其外形特征(圖1)，進而決定其抗側性能，即墻板高度H、寬度B、墻板厚度t、波長Cl、波高Ca和波折角度θ。相比平鋼板墻只有H、B和t的情況，波折墻板的幾何選型復雜的多。

如前所述，上下框架梁的約束對豎放波折墻板影響很大。隨著層高的增加，框架梁的約束作用減小，導致墻板的面外變形增大、面內剪切抗側效率降低。圖8 給出了不同高度下墻板的抗側曲線，隨著墻板高度增大其初始剛度及承載力均有所下降，尤其屈曲后抗側曲線更為明顯。

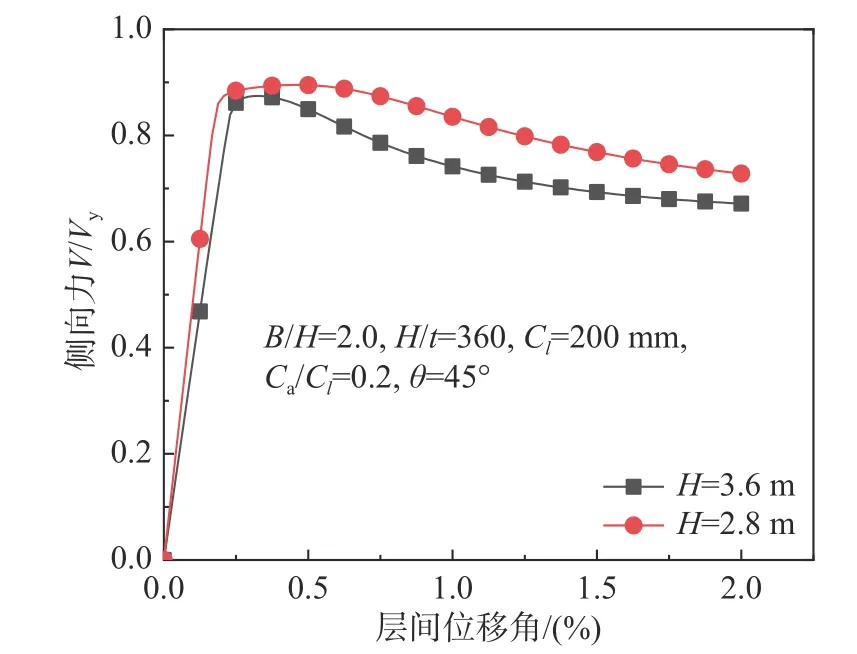
圖8 墻板高度對抗側承載力的影響Fig. 8 Effect of wall panel height on lateral resistance

因此，根據相關國家規范[29?31]，為了滿足墻板選型的適用性，后續分析中波折墻板高度均偏于保守地取為H=3.6 m，采用Q235 鋼，屈服強度fy=235 MPa。對于其他墻板參數的選取，結合前人研究，涵蓋工程常用范圍：B/H=0.5～2.0，H/t=240～900，Cl=300～700 mm，Ca/Cl=0.10～0.20，θ=30°～90°。

3.1 波折角度

保持其他參數不變，變化波折角度進行推覆分析，典型算例結果如圖9 所示。隨著波折角度θ 的增加，墻板的抗側承載力尤其是屈曲后承載性能明顯提升。這是因為，增大波折角度豎放墻板繞強軸的彎曲剛度將會增大[17]，從而減小波折板的面外變形，改善其面內抗側受力。因此，在墻板選型設計中，在條件允許時建議選擇較大的波折角度。其他算例得到類似結論，在此不贅述。

圖9 子板面波折角度對抗側承載力的影響Fig. 9 Effect of sub-panel inclined angle on shear resistance

3.2 墻板寬高比

選取算例：①H=3.6 m，H/t=600，Cl=500 mm，Ca/Cl=0.10，θ=45°；②H=3.6 m，H/t=450，Cl=600 mm，Ca/Cl=0.10，θ=45°；③H=3.6 m，H/t=360，Cl=400 mm，Ca/Cl=0.20，θ=45°，變化墻板寬高比B/H=0.5～2.0進行單向推覆分析，提取極限承載力和殘余承載力如圖10 所示。同時，圖11 給出了算例3 中B/H=1.0時墻板殘余承載力對應的主應力狀態。

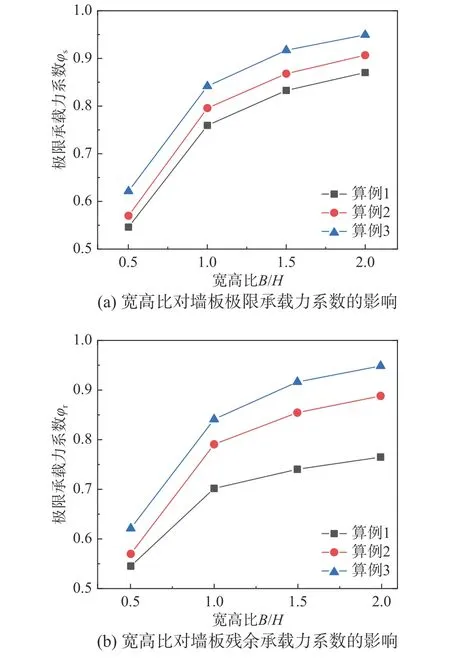
圖10 寬高比對墻板承載力系數的影響Fig. 10 Effect of aspect ratio on strength coefficient

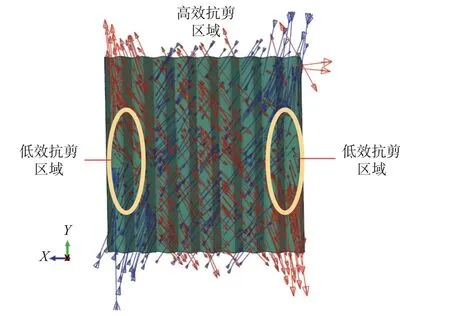
圖11 墻板主應力(層間位移角2.0%時)Fig. 11 Principal stress distribution (drift ratio 2%)

可以看到，同一組算例隨著寬高比的增加，墻板承載力系數增大，這表明抗側效率提高，但增長速度逐漸變緩。這是由于墻板兩側邊無有效約束，附近存在“低效抗剪區”(圖11)，使部分墻板不能有效參與抗側；而寬高比越大即墻板越寬，自由邊的低效抗剪區所占墻板總面積的比例越小，對承載力影響也相應減小。

圖12 為算例3 中不同寬高比下殘余承載力狀態即最大層間位移角時墻板屈服情況(陰影區表示屈服，非陰影區表示未進入屈服)。當寬高比較小時(B/H=0.5)，無約束自由側邊的影響很大，墻板大部分區域沒有有效參與抗剪進入屈服，導致承載力系數較小。當寬高比增大到2.0 時，未進入屈服的低效抗剪區占比很小，墻板表現出較高的極限承載力系數和殘余承載力系數，抗側性能接近四邊連接墻板。

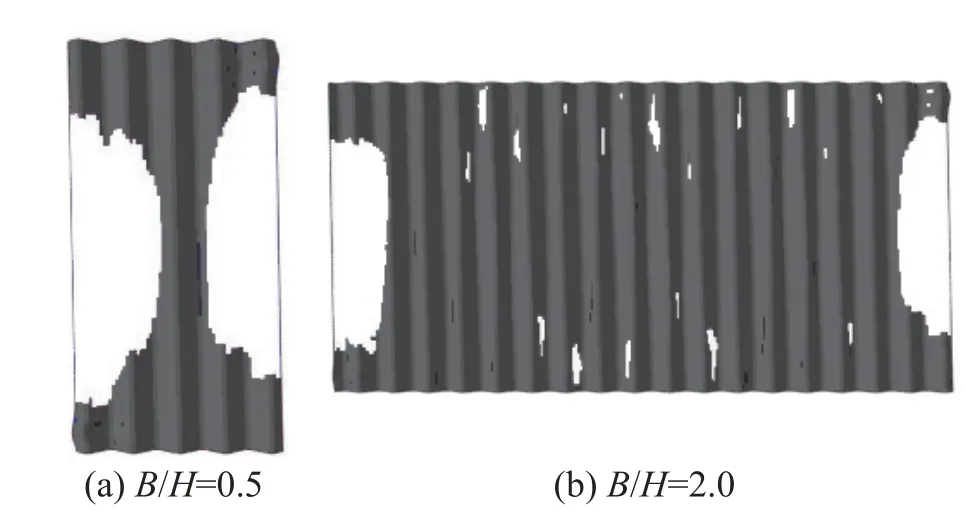
圖12 寬高比對墻板屈服面積的影響Fig. 12 Effect of aspect ratio on yield area of wall

3.3 波形比

波形比Ca/Cl是波折墻板區別于平鋼板的最大特征。典型算例的單向推覆抗側曲線隨波形比的變化如圖13 所示。當波形比過小時(<0.10)，墻板的屈曲后承載力下降較快，殘余承載力較低，延性較差。

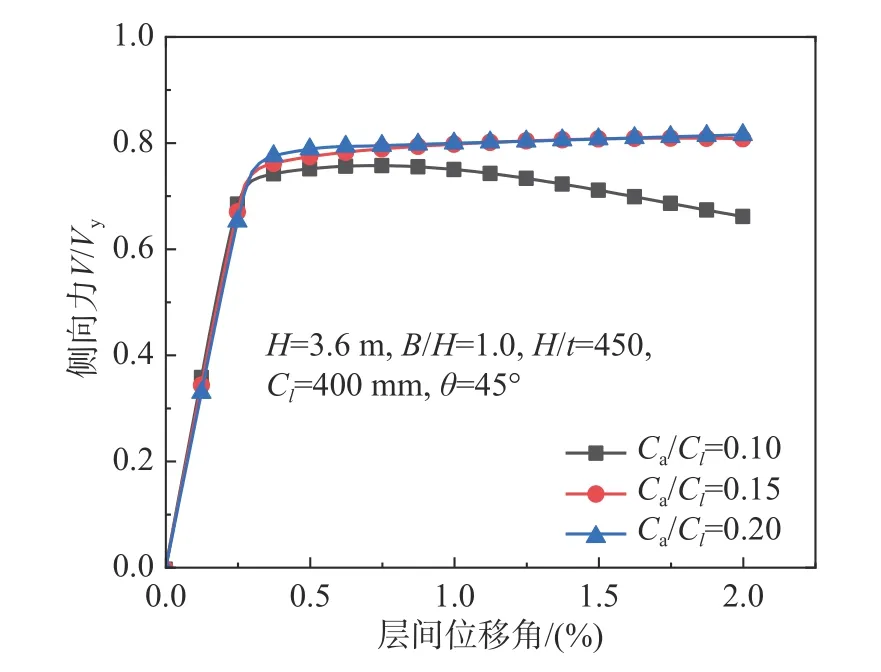
圖13 波形比Ca/Cl 對承載力的影響Fig. 13 Effect of corrugation ratio on lateral resistance Ca/Cl

如圖14 所示，不同波形比下墻板的面外變形模式相似，但Ca/Cl=0.10 時最大變形為112 mm，而Ca/Cl=0.15 時，墻板面外剛度顯著增大，面外變形減小至僅為54 mm。墻板面外變形過大，使得墻板不再處于完全的面內純剪狀態，其承載力隨著面外變形的增大而下降。其他算例下的結果類似，在此不贅述。研究分析表明[27]，過大波形比可能引起波折墻板發生相關屈曲破壞而導致承載力下降，因此在初步設計時，建議Ca/Cl在0.10～0.20 范圍內取值。

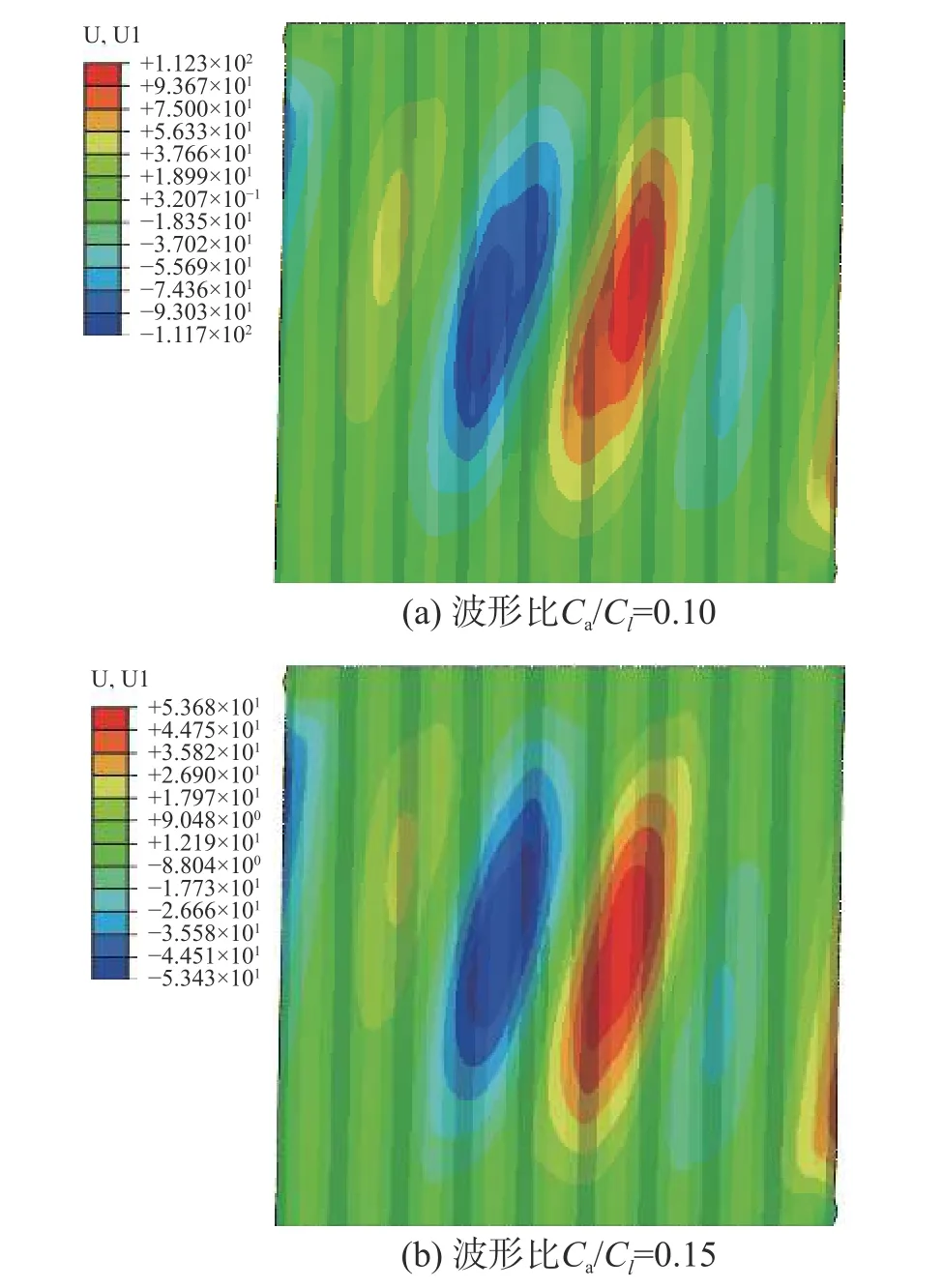
圖14 不同波形比墻板的面外變形(層間位移角2%)Fig. 14 Out-of-plane deformation of panels with different corrugation ratios (drift ratio 2%)

3.4 高厚比與波長

如圖15 所示，隨著墻板高厚比H/t的減小(厚度增大)，其面外剛度增大面外變形減小，更接近面內抗剪受力狀態，因此，承載力尤其是屈曲后承載力提高且更加穩定。

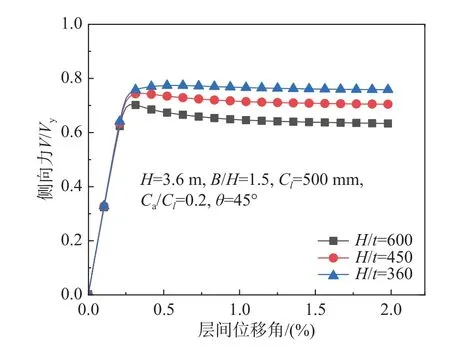
圖15 高厚比對承載力的影響Fig. 15 Effect of height-to-thickness ratio on lateral resistance

墻板的波折長度Cl也是一個重要參數。圖16的算例結果表明，波折長度對屈曲后承載性能及殘余承載力系數影響較大。此外，隨波折長度的增加，墻板殘余承載力系數先增大后減小，也就是說存在最優波長，使得墻板的抗側性能最優。

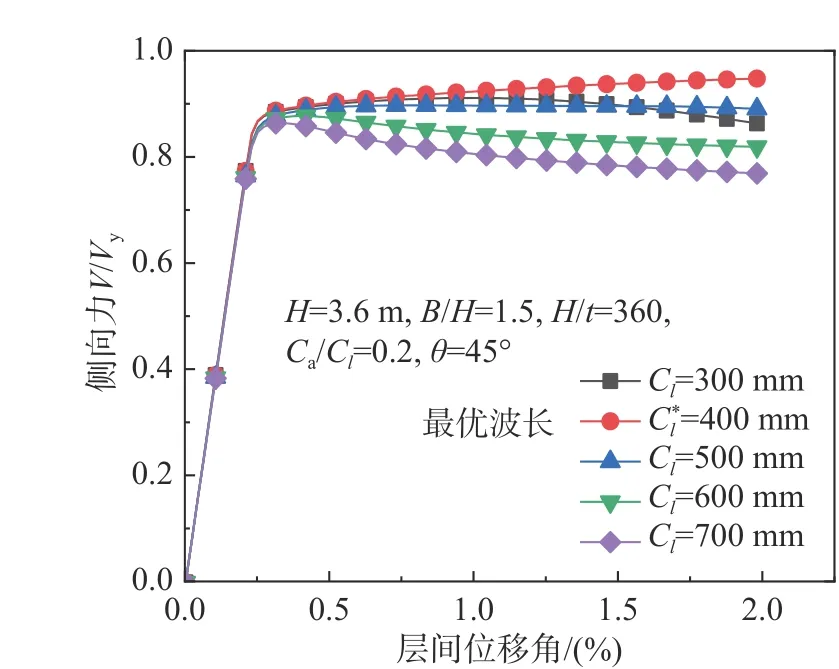
圖16 波長對承載性能的影響Fig. 16 Effect of corrugation length on lateral resistance

從圖17 和圖18 可以看到，當波長Cl=400 mm時，墻板在殘余狀態下發生整體面外變形，但變形量較小，因此大部分區域的主應力為45°方向，即處于純剪狀態；當波長增大到700 mm 時，發生類似“拉力帶”的局部變形，主應力方向改變，墻板不再是面內純剪狀態，導致抗側曲線的下降。

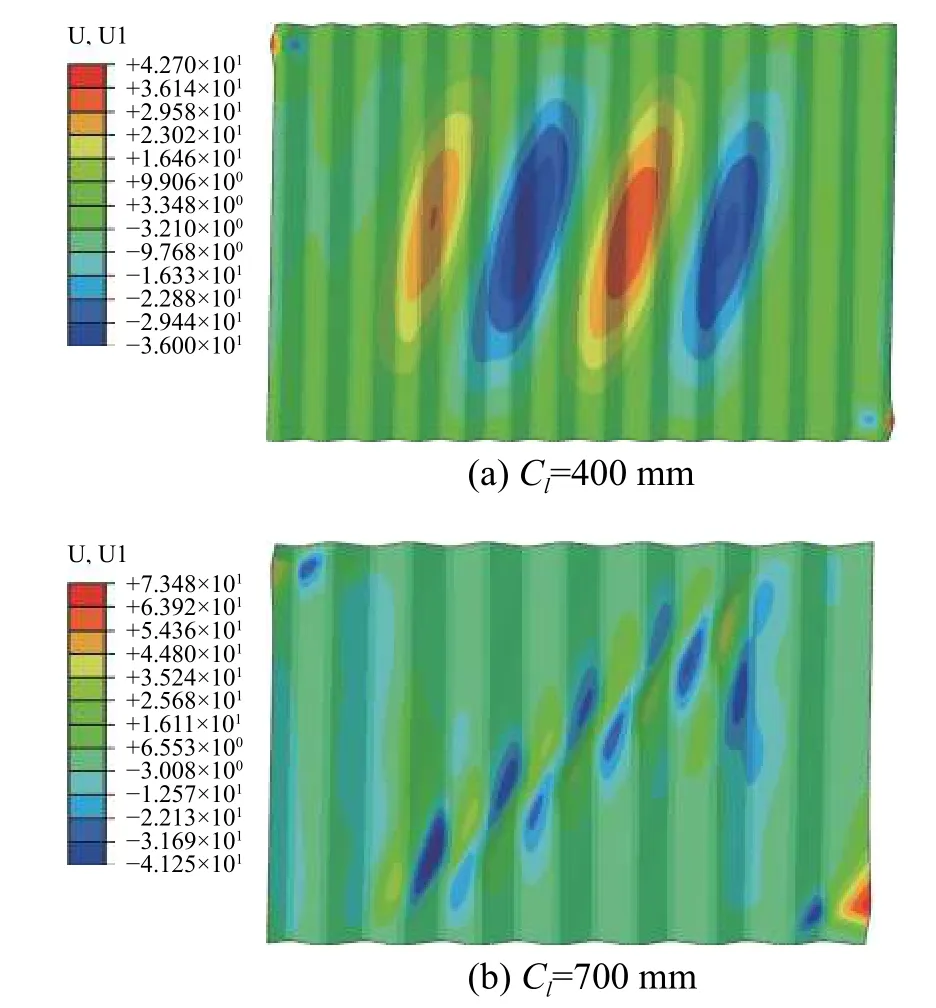
圖17 不同波長墻板的面外變形(層間位移角2%)Fig. 17 Deformation of corrugated panels with different corrugation length (drift ratio 2%)

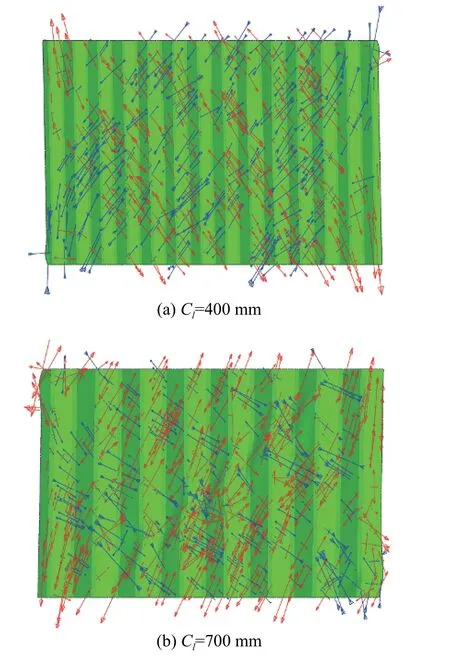
圖18 不同波長墻板的主應力(層間位移角2%)Fig. 18 Principal stress distribution of wall panels with different wavelengths (drift ratio 2%)

正是由于波長變化引起墻板面外變形破壞模式的改變，進而影響了墻板的抗側穩定性能，導致最優波長的存在。為了得到最優長細比Cl*，進行大量變參數分析，發現最優長細比Cl*與其他幾何尺寸之間存在如下關系：

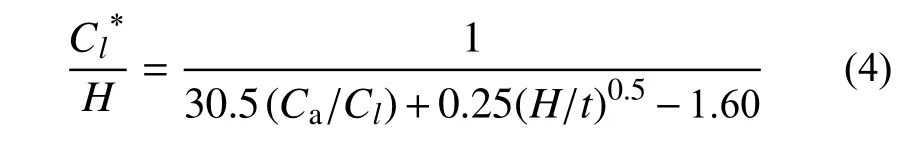
擬合式(4)與有限元結果對比如圖19 所示。以圖16 中的算例為例，由式(4)可得最優波長Cl*≈390 mm，與有限元結果Cl=400 mm 接近。

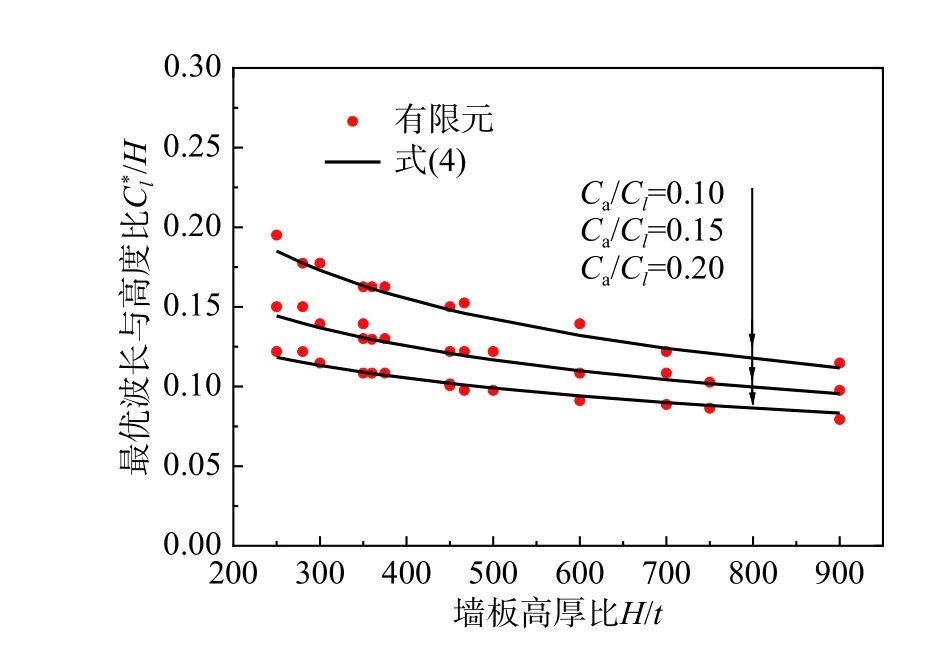
圖19 最優波長結果Fig. 19 Result of optimal corrugation length

綜上，在進行墻板的選型設計時，寬高比宜B/H≥1.0，波形比宜Ca/Cl≥0.15，波折角度宜θ≥45°，并根據式(4)確定最優波長Cl*，以使墻板具有較高的極限承載力、殘余承載力及足夠的延性性能。

4 兩邊加勁豎放波折墻板

由3.2 節可知，兩邊連接波折墻板的兩自由邊存在低效抗剪區。為了提高墻板的抗側效率，本節對豎放波折墻板兩側自由邊設置加勁構件，對加勁效果進行分析，提出加勁構件的設計建議。

4.1 加勁構件形式

兩邊連接豎放波折墻板中，兩側加勁構件提供了約束作用限制板邊的面外變形，因此，加勁構件可不與框架梁連接，此時，暫不考慮加勁構件平面內抗彎剛度的影響。選用兩種形式的加勁構件，單塊鋼板和方鋼管(圖20)，分別對典型算例設置兩種加勁構件，抗側性能如圖21 所示。每組算例中，兩種加勁構件的面外抗彎剛度相同，但方鋼管的扭轉剛度要顯著大于加勁平鋼板。

圖20 加勁構件的形式Fig. 20 Form of stiffening member

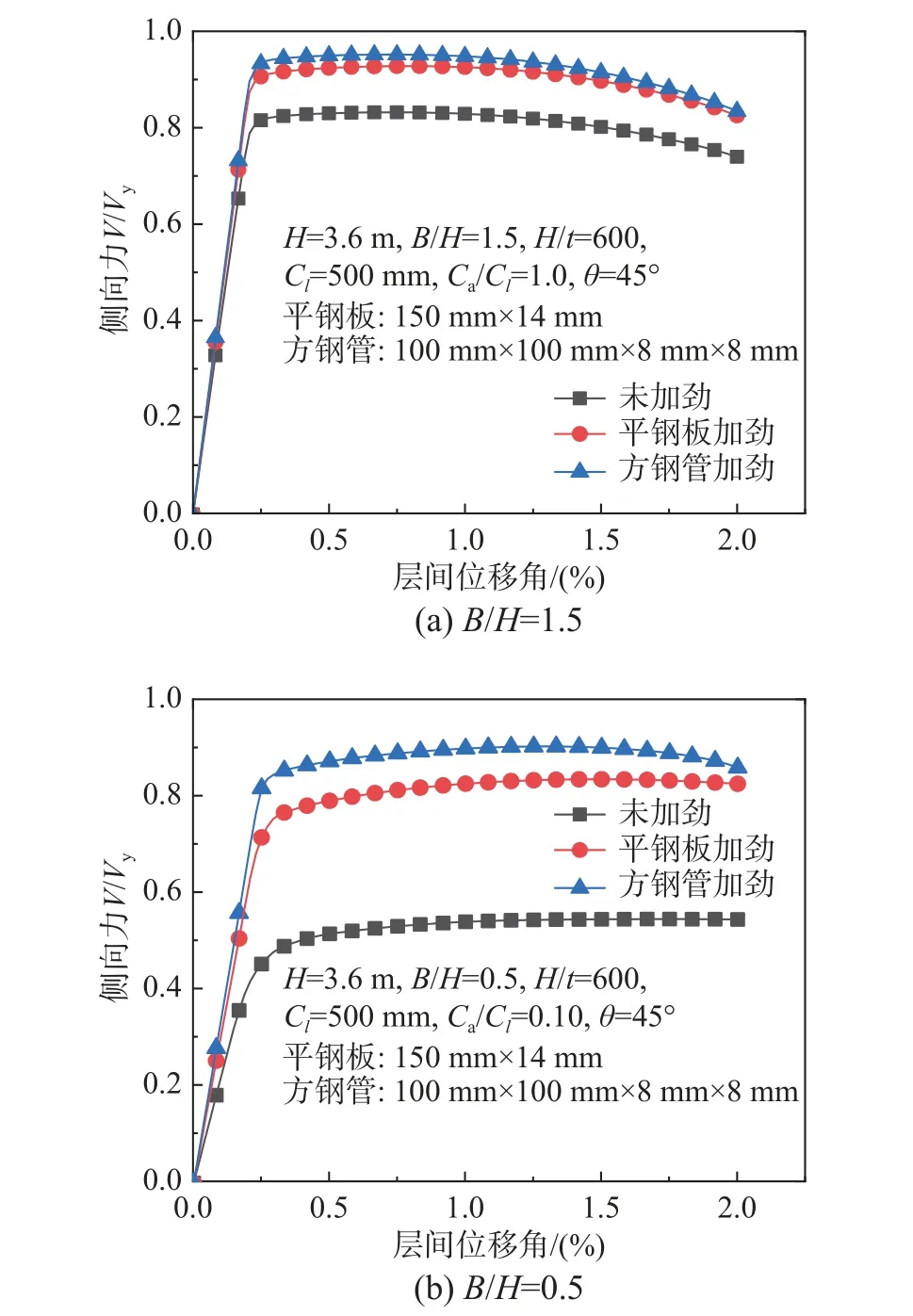
圖21 墻板加勁構件對抗側性能的影響Fig. 21 Effect of stiffeners on the lateral resistance

結果表明，邊緣加勁構件可顯著提升豎放波折墻板的極限承載力和殘余承載力。對于大寬高比墻板(B/H=1.5)，加勁構件的扭轉剛度則對加勁效果幾乎沒有影響，主要是其面外抗彎剛度的貢獻；對于小寬高比墻板(B/H=0.5)，扭轉剛度有一定影響，但相比面外剛度仍然較小。

此外選取圖22 的兩個算例，加勁構件的面外抗彎相同但面內抗彎剛度不同，且加勁構件與框架梁相連。可以看到，加勁構件的面內剛度對墻板的抗側性能幾乎沒有影響。其他算例得到類似結論，在此不贅述。

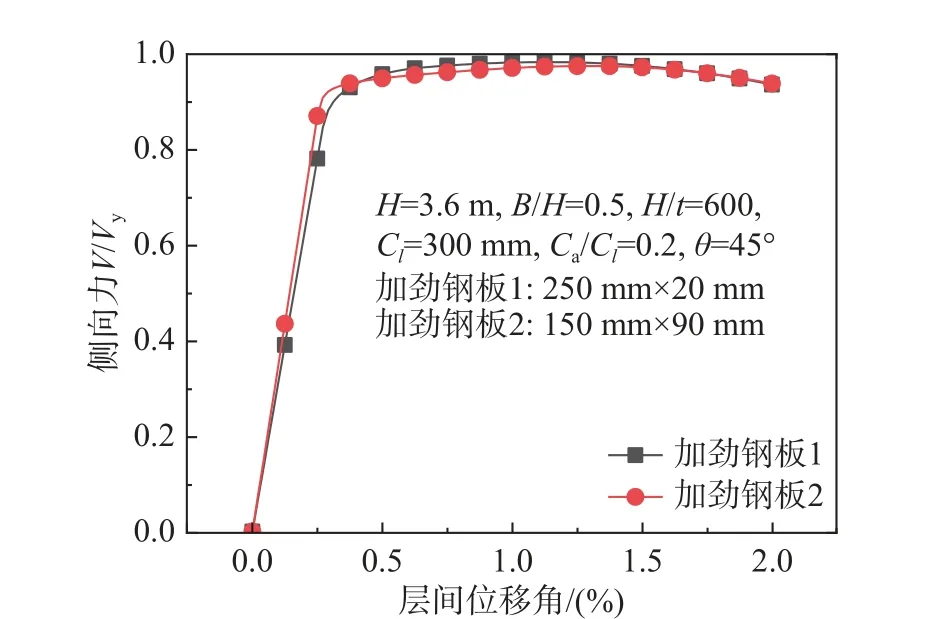
圖22 加勁構件面內抗彎剛度對抗側性能的影響Fig. 22 Effect of in-plane flexural stiffness of stiffening members on lateral resistance

綜上，加勁構件的面外抗彎剛度對加勁效果起到決定性作用。在設計中，加勁構件建議選用方鋼管，其截面開展、加勁效果更好。

4.2 界限約束剛度比

為了反映邊緣加勁構件對墻板兩側邊的約束強弱，引入約束剛度比η 參數，定義為加勁構件面外抗彎剛度與內嵌墻板抗彎剛度之比，即：

式中：Is為加勁構件的平面外抗彎慣性矩；Dx為墻板的強軸彎曲剛度；H為墻板的高度[17]。

選取典型墻板算例，變化加勁構件的剛度，得到墻板殘余承載力系數如圖23 所示。可以看到，當加勁構件的面外抗彎剛度較小時，墻板的殘余承載力系數隨著約束剛度比的增大而顯著提高；隨著約束剛度比的繼續增大，殘余承載力系數的增速減緩，這說明已起到了充分加勁作用。此外，對于不同寬高比的墻板，加勁構件的加勁效率也有所不同：寬高比較小時(B/H=0.5)，承載力提高程度更高，但達到充分加勁(即曲線接近走平)所需的約束剛度比也越大。

從上述算例結果可知，當約束剛度比η≥0.60 時，墻板的殘余承載力系數已超過完全約束時的90%，此時可認為加勁構件為墻板兩側邊提供了充分的支承和約束作用，對于其他墻板具有相同的結論，在此不再一一給出。

因此，本文將η*=0.60 定義為“界限約束剛度比”。當加勁構件采用界限約束剛度比時：一方面改善了墻板的抗側性能；另一方面隨著墻板的寬高比增大，加勁效果逐漸減弱(圖23)。這也與前述分析結論一致：寬厚比越小的墻板其兩側自由邊的影響越大，因而更需要進行加勁。圖24 給出了算例1 中B/H=0.5 的墻板在未加勁和界限約束剛度加勁下，達到最大層間位移角時墻板的屈服區域。可以看到，加勁后墻板的低效抗剪區域明顯減小，承載性能得到顯著提升。

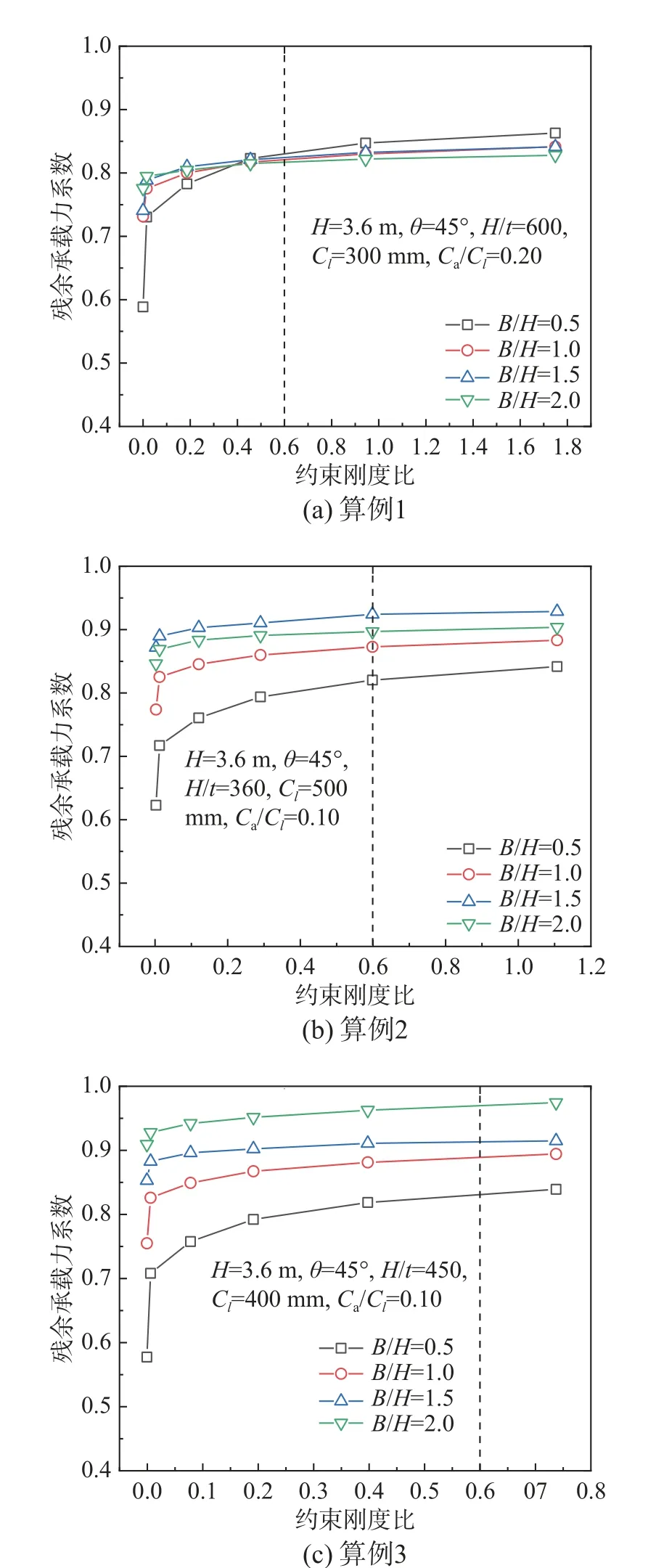
圖23 加勁構件約束剛度比的影響Fig. 23 Effect of restraint stiffness ratio on lateral resistance

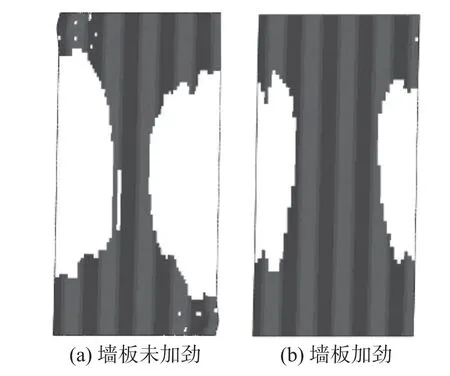
圖24 墻板加勁前后屈服區域對比(層間位移角2%)Fig. 24 Yielding areas before and after stiffening for corrugated panels (drift ratio 2%)

5 往復加載下的抗側性能及設計

波折鋼板剪力墻的內嵌墻板作為抗側構件，在地震作用下應當具有足夠的變形和耗能能力，起到消能減震的作用。本節對兩邊連接加勁豎放波折墻板在往復荷載作用下的滯回性能進行分析。通過在上部梁端施加水平位移實現往復加載，按照層間位移角±0.5%、±1.0%、±1.5%、±2.0%的四個級別施加，每一級加載循環一次。

5.1 墻板的滯回曲線及骨架曲線

選取第2 小節單向推覆分析中弱墻板的典型算例：H=3.6 m，B/H=1.5，H/t=600，Cl=400 mm，Ca/Cl=0.10，θ=45°。圖25(a)給出了墻板的滯回曲線，當層間位移角超過±0.5%后，峰值承載力隨著位移角的增加而顯著下降，表明墻板屈曲后抗側性能極不穩定，影響了其延性和耗能能力。

圖25(b)為墻板滯回分析的骨架曲線和單向推覆下抗側曲線的對比。當層間位移角小于±1.0%時，骨架曲線與單向推覆曲線基本重合；但當層間位移角繼續增大超過±1%后，骨架曲線呈現出明顯的強度退化現象，最大層間位移角對應的殘余承載力比單向推覆時降低了18%。究其原因，在于往復加載下面外殘余變形在每個加載循環中不斷的積累增大，導致加載后期墻板的變形將非常顯著，大于單向推覆時同等層間位移角下的面外變形，因此承載力更低一些。

同樣，對于單向推覆分析中的強墻板，選取典型算例：H=3.6 m，B/H=1.5，H/t=360，Cl=400 mm，Ca/Cl=0.20，θ=45°，分析結果如圖26 所示。可以看到，墻板滯回曲線飽滿呈梭形。并且隨著層間位移角的增大，極限承載力逐漸上升，直至層間位移角2%時，這意味著強墻板具有穩定的承載力、足夠的延性和良好的耗能能力。

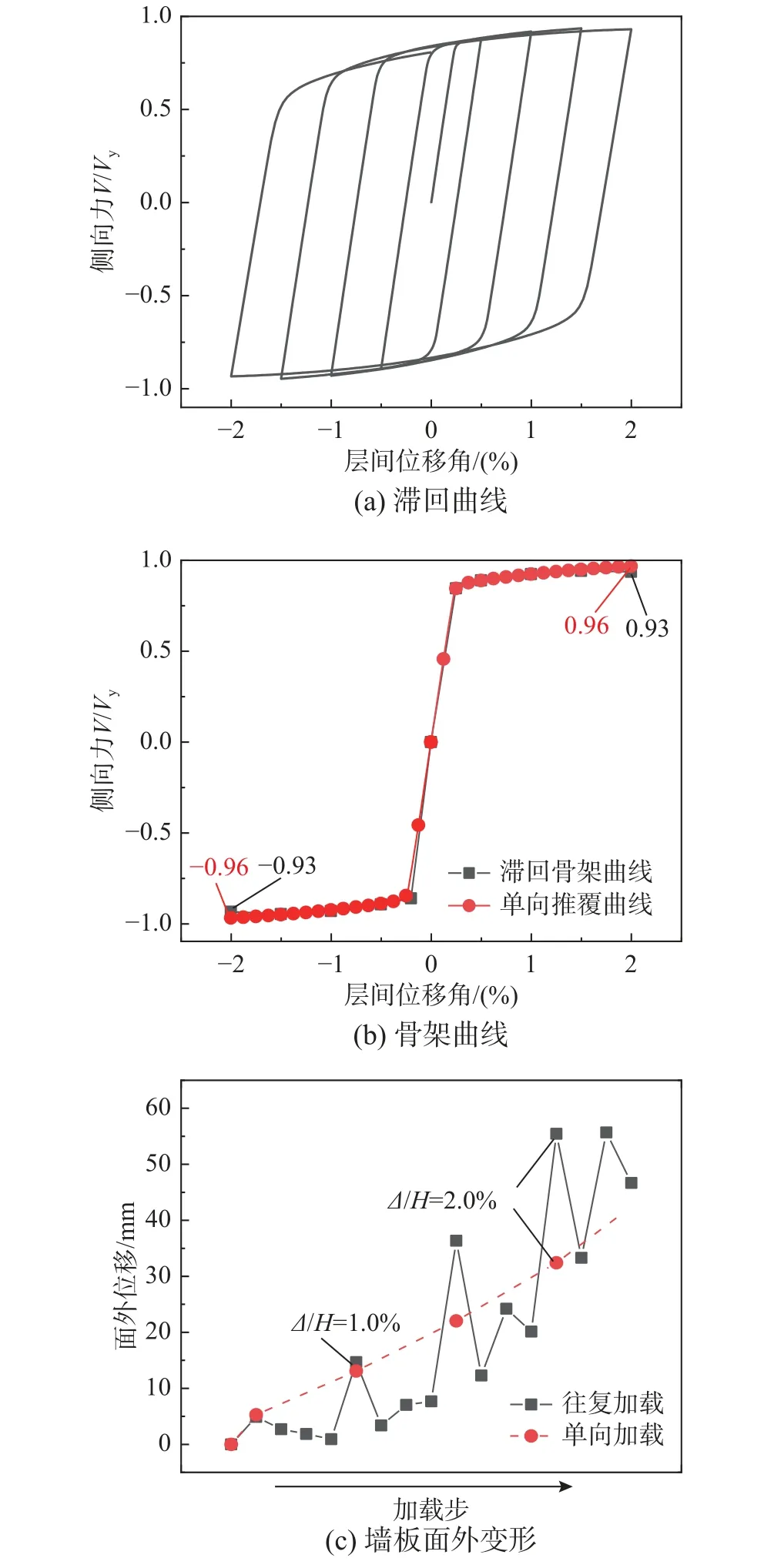
圖26 單向推覆與滯回分析對比(強墻板)Fig. 26 Comparison of monotonic pushover and hysteresis analysis (strong wall panel)

圖26(b)表明，與弱墻板不同，強墻板的滯回骨架曲線與單向推覆曲線基本重合。這是由于盡管往復加載下墻板面外變形仍不斷積累，但此強墻板在層間位移角2%時最大面外變形只有55 mm，且與單向推覆下的面外變形量比較接近(圖26(c))。

5.2 墻板優化設計建議

如前所述，對于內嵌波折墻板，其優越的抗側及滯回性能的發揮依賴于墻板參數例如寬高比、高厚比、波折角度、波長和波形比等的合理取值，設計中應避免選擇“弱墻板”。但由于影響參數眾多，波折墻板的初步設計選型是一件復雜且困難的事情。因此，如何合理選擇墻板參數，使其具有良好的抗側承載力、延性變形及耗能能力，是設計人員急需的。

5.1 節分析表明，由于往復加載下墻板的面外累積變形，會導致滯回分析的骨架曲線通常低于單向推覆曲線。在抗震設計中，墻板的滯回性能相比單向推覆性能更為重要，因此，本節基于往復加載分析，提出兩邊連接加勁豎放波折墻板的優化選型建議。選定墻板性能的優化目標為：在往復加載下達到最大層架位移角2.0%時的殘余承載力系數φr≥0.85，同時φr/φs≥0.85，后者保證了墻板在最大層間位移角時仍有足夠的承載力，即骨架曲線沒有明顯的強度退化，具備良好的延性變形和耗能能力。此外，優化分析模型中加勁構件與框架梁剛接，其約束作用更大。

在第3 節的墻板參數取值范圍內進行大量變參數分析，共128 個算例，從中選擇滿足上述優化目標的參數組合，最終確定墻板優化選型如表1所示。本表適用于鋼材等級等于或低于Q345、同時采用方鋼管加勁構件且滿足界限肋板剛度比η*≥0.60 的情況。可以看到，采用優化選型的墻板后，在墻板層間位移角2%時依具有足夠的抗側能力(φr≥0.85)。設計人員設計波折墻板時，可根據水平荷載首先確定墻板的寬度和厚度，再基于表1根據寬高比和高厚比確定其他參數使得墻板的抗側性能達到最優。

設計兩個優化墻板，對表1 的適用性進行驗證：①H=3.2 m，B/H=0.5，t=8 mm，Cl=400 mm，Ca/Cl=0.15，θ=60°；②H=3.0 m，B/H=1.0，t=12 mm，Cl=500 mm，Ca/Cl=0.1，θ=75°，滯回曲線如圖27所示。可見，根據優化選型表進行初步設計得到的墻板其滯回曲線飽滿，承載力穩定，具有很好的延性和耗能能力。

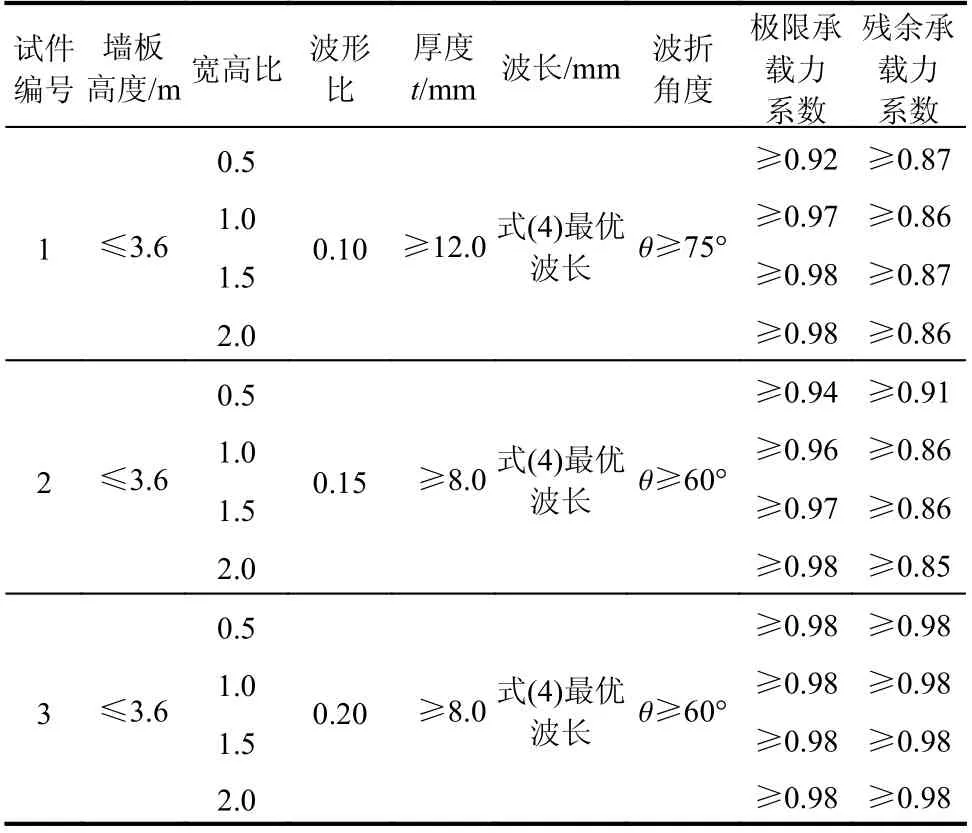
表1 豎放波折墻板優化選型表Table 1 Recommended configurations for corrugated panels

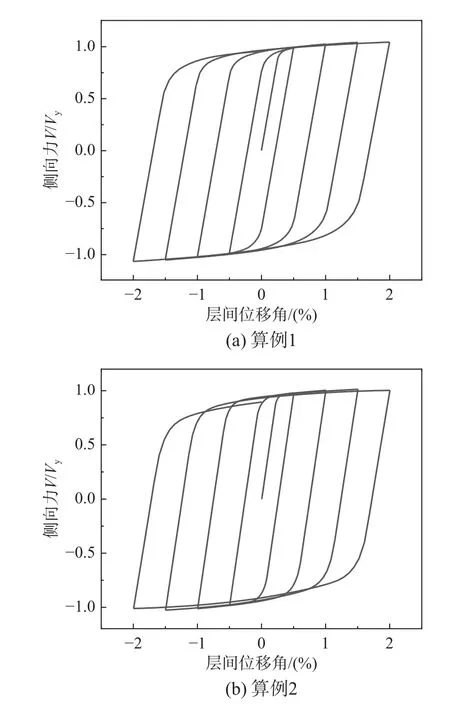
圖27 優化選型墻板的滯回曲線Fig. 27 Hysteresis curve of optimized panels

6 結論

本文研究了兩邊連接豎放波折鋼板剪力墻中內嵌墻板在單向推覆和往復荷載下的抗側性能，揭示了關鍵參數的影響規律，并提出了墻板的優化選型表供設計人員參考和使用。主要結論如下：

(1)墻板的波折角度越大，其屈曲后承載性能明顯改善。波形比過小時墻板的屈曲后承載力下降較快。在其他幾何參數給定的條件下，根據擬合公式可得到最優波折長度。

(2)兩邊連接豎放非加勁波折墻板當寬高比較小時，兩側自由邊的低效抗剪區占比較大，削弱了其抗側性能。可對墻板自由邊加勁以提高其抗側能力。

(3)加勁構件面外彎曲剛度是提高其加勁效果的主要影響因素。當加勁構件滿足界限約束剛度比時，墻板的自由邊可獲得充分約束。

(4)本文提出兩邊連接加勁豎放波折墻板的參數優化取值，設計人員可直接查詢相關表格進行初步選型設計，能夠保證墻板具有較高的極限承載力、良好的屈曲后承載力、延性變形和耗能能力。