定積分概念的教學探究

陳玉清

金肯職業技術學院 江蘇南京 211156

數學是自然科學的重要基礎，應用于現代社會的方方面面，運用符號運算、形式推理、模型構建等方式，表達現實世界中事物的本質、關系和規律[1]。數學概念是數學的基礎內容，是數學判斷和推理的依據。如不理解概念，在解決數學問題時，往往會碰到很多困難。特別是對同一數學概念的不同表達形式、概念之間的相互關系等缺乏系統概括的理解[2]。微積分是高等數學的主要內容，正確理解導數、微分、定積分的概念，是理解、記憶微積分中涉及的公式、符號、定理及解題的核心。定積分是積分學教學中的重點和難點。如何在教授定積分的過程中，讓學生更好地理解、接受定積分，并激發學生的學習興趣，培養學生邏輯推理、分析、歸納、總結的能力以及創新能力是教學中值得研究的課題。

一、定積分概念的教學探究

(一)教學背景

當今社會，科技迅猛發展，“數學”課程的教學方法與教學手段必然隨之改變。傳統的“黑板+板書”的教學模式無法適應于信息化時代下成長的學生，特別是“數學”課程中的數學概念抽象、難以理解、推導過程復雜，使高職學生心存畏懼。將合適的信息技術運用到教學中，使教學內容更清晰化，將有利于學生理解并接受，同時能培養學生的創新能力。數學是一門抽象的學科，特別是數學概念，如能借助合理的信息技術作為輔助，從而提高教學質量、課堂容量、學生學習興趣。授課前期，以微積分發展史及涉及相關數學家的故事作為引入，讓學生了解數學的重要性和數學家們的偉大貢獻，以及他們孜孜不倦、一絲不茍、鍥而不舍、堅持不懈的精神品質。

(二)教學目標及教學方法

1.教學目標

知識目標：理解并掌握定積分的概念、幾何意義；結合實例，簡單了解定積分知識的實際應用；能力目標：在定積分概念形成過程中，培養學生的抽象概括能力，提高學生分析問題、解決問題的能力；素養目標：讓學生了解定積分的概念形成背景，培養學生探索數學的興趣。

2.教學重點、難點

定積分的概念與思想，定積分概念的理解及應用[3]。

3.教學方法

多媒體運用，啟發式引導，理論與實際相結合。

(三)教學過程

1.新課引入

有效的引入不僅能激發學生的學習興趣，更有助于學生對后續要學習的知識的理解與掌握[4]。

簡單介紹微積分發展簡史，突出微積分的重要性：微積分的誕生，帶來了工業革命，有了大工業生產，繼而有了現代化的社會：航天飛機宇宙飛船，及現代化的交通工具等[5]，很多自然科學、幾何學的概念中都需要定積分。促使學生重視數學，重視知識的力量。定積分是對連續變化過程總效果的度量，求曲邊梯形的面積是定積分概念最直接的起源[5]，引出第一個引例的教學。

2.介紹兩個典型例子

第一個典型例子：曲邊梯形的面積。

定積分是為了計算平面上封閉曲線圍成的平面圖形的面積而產生的，規則平面圖形面積在中學階段已經解決，讓學生回顧已學習過的規則圖形及其面積公式，進一步引出不規則平面圖形的面積如何解決的問題。為了引起學生的學習興趣，可以從實際生活中尋找這種不規則圖形，進而提出問題。

對學生提出“如何求出這種不規則圖形的面積呢？”的問題，啟發學生思考，并給出一個不規則圖形，使用信息技術手段分割所給不規則圖形為規則圖形和不規則圖形1：

以不規則圖形中其中某部分為例進行研究，曲邊梯形的概念及計算其面積的問題，給出曲邊梯形的概念。

曲邊梯形的概念：曲邊梯形是由連續曲線y=f(x)(f(x)≥0)及三條直線x=a，x=b，y=0所圍成的平面圖形，如圖2：

設曲邊梯形的面積為A，利用信息技術手段向學生展示如何分割曲邊梯形，將分割出來的其中某一個窄曲邊梯形與和它同底的小矩形面積比較，如圖3和圖4所示：

分析：由于曲邊梯形在底邊上的各點處的高f(x)在區間[a，b]上是變動的，因此面積A不能直接用矩形或梯形的面積公式計算。但由于曲邊梯形底邊上的高f(x)在區間[a，b]上是連續變化的，如果曲邊梯形的底邊很短，則高f(x)變化不大，可近似地看作不變化，因此自然想到用小矩形的面積之和逼近曲邊梯形的面積A。

再進一步展示圖5：

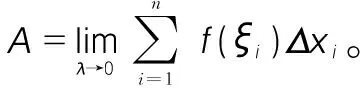
第二個典型例子：變速直線運動的路程。

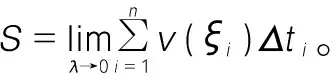
3.定積分的概念的具體內容

讓學生結合上述兩個典型例子，自主閱讀概念內容，對于定義中給出的函數f(x)，啟發學生說出在上述實例中f(x)是指曲邊梯形的面積中曲線y=f(x)，在變速直線運動的路程中是指速度v=v(t)，定義中的f(ξi)△ti在曲邊梯形的面積問題中是指第i個小矩形的面積，在變速直線運動的路程問題中是指第i個小時間段上路程的近似值，結合實際問題理解定義，抽象的問題顯得更加形象化，便于基礎薄弱的學生加以理解。

4.用定積分解決實際問題問題，體現定積分的作用，啟發學生學習興趣

用定積分解決新課引入部分圖1面積問題。圖7～圖9為擬合出的污染面積及分布在各象限內的邊界函數，

以第一象限為例，在第一象限內，邊界函數為：

利用定積分的方法可得到第一象限的圖1的面積為：

其中S1為第一象限內的圖1的面積。理論知識與實踐相結合的教學模式，既能調動學生的學習興趣，又能讓學生感受到數學的實際應用的重要性，從而激發學生熱愛數學，進而努力學習數學知識。

5.定積分的幾何意義的介紹

利用多媒體手段，結合曲邊梯形的面積展示圖形，介紹定積分的幾何意義，學生可以直觀上體會并理解。幾何意義的介紹，對后續定積分的應用起到鋪墊作用。

6.思政內容的引入

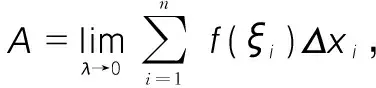
二、結論

上述的教學方式及教學過程以學生為教學導向，針對高職層面的學生實際情況，合理安排教學內容，選擇科學的教學方法與手段，使學生更加容易接受數學，更好地學好數學，為學習其他專業課打好基礎。運用觀察、分析、比較、歸納等數學方法，不僅引導學生接受并吸收所學知識，更重要的是在傳授知識的過程中，訓練了學生數學思維及數學邏輯，培養了學生的創新能力，使其思維的廣度、深度和創造性得到進一步加強[6]。