改進貪心算法求解擴展簡化折扣{0-1}背包問題①
林洪, 鄧艷
中國人民武裝警察部隊警官學院 基礎部,成都 610213
折扣{0-1}背包問題(discounted {0-1} knapsack problem,D{0-1}KP)作為{0-1}背包問題的拓展[1-7],因其能刻畫物品選擇與否對其他物品的影響關系而受到廣泛關注.D{0-1}KP在項目決策、投資與預算控制等方面具有廣闊的應用背景[5,7].
傳統D{0-1}KP模型每個項集中物品僅有兩個物品,通過在項集中增加一個物品來表示項集中兩個物品同時被選擇的情況.當同一項集中物品個數較多時,傳統D{0-1}KP較難投入應用.
擴展簡化折扣{0-1}背包問題(extended simplified discounted {0-1} knapsack problem,ESD{0-1}KP)作為D{0-1}KP的拓展,相對于D{0-1}KP,ESD{0-1}KP增加了每個項集中物品的數量,且折扣關系也更加貼合實際情況.
ESD{0-1}KP利用遺傳算法[3-4,7]、粒子群算法[6]、帝王蝶算法[8]等對問題進行求解,但隨著單個項集中物品數量的增加,貪心修復操作難度加大,現有貪心策略算子[9](greedy strategy operator,GSOR)效果值得改進.
文章基于GSOR,通過在每個項集中增加一個價值質量均為0的虛擬物品,將ESD{0-1}KP轉化為多選擇背包問題[10-11](multiple-choice knapsack problem,MCKP),結合改進帕累托算法(improved pareto algorithm,IPA)[12],提出新型貪心策略算子(new greedy strategy operator,NGSOR).利用4類ESD{0-1}KP大規模實例進行仿真,分析NGSOR性能.
同時通過數學轉化,從理論上證明ESD{0-1}KP與MCKP是完全等價的,意味著傳統上求解MCKP的算法均可通過NGSOR的操作進行轉化求解,為D{0-1}KP和ESD{0-1}KP的后續研究奠定了基礎.
當前對于ESD{0-1}KP問題的研究較少,且僅考慮了每個項集中存在3個元素,合計8種情況的約束.隨著項集規模的不斷增加,相比傳統D{0-1}KP,ESD{0-1}KP模型與算法得到進一步泛化.同時,考慮到當前ESD{0-1}KP僅有項集內3個物品的數據集和已有算法結果,為了便于討論和對比,模型與算法均考慮項集3個物品的情況.
1 ESD{0-1}KP模型
為了更加貼合實際商業模型,假設每個項集包含3個物品.對于項集中的物品,若僅購買一個物品,則物品質量乘d3i-2;若購買兩個物品,則對兩個物品質量之和乘d3i-1;若項集中物品均被購買,則對其質量之和乘d3i.折扣系數滿足:
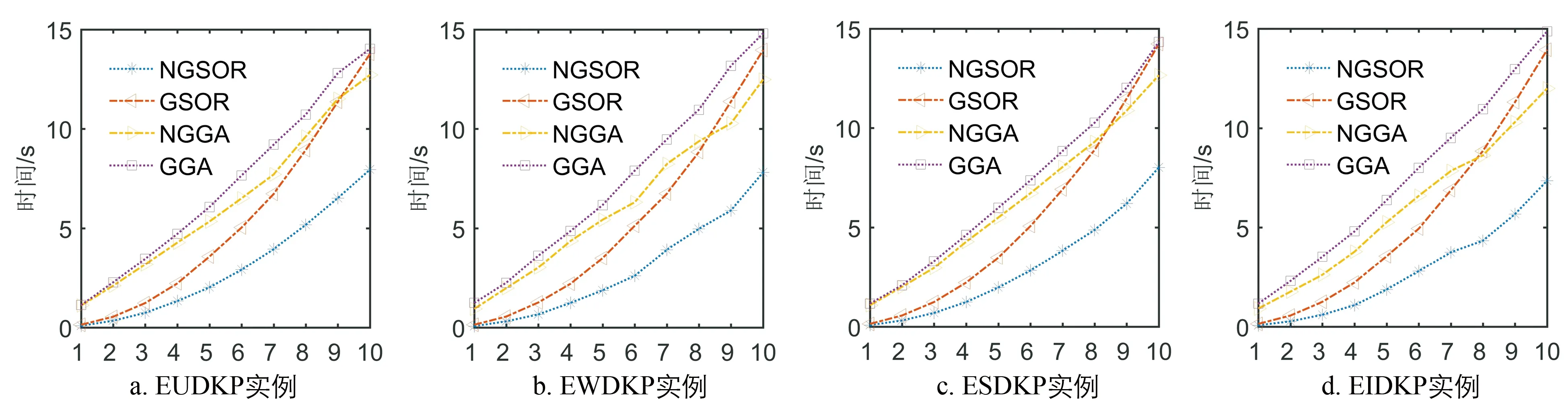
0 (1) d3i-2>d3i-1>d3i (2) 為便于討論,記 Di=[d3i-2,d3i-1,d3i] (3) 記問題的決策變量為X=[x1,x2,…,x3n]∈{0,1}3n.將決策變量中已選擇的物品記為集合K.對于?i∈N,若 xi=1 (4) 則i∈K,且Kj={i|i∈K,3j-2≤i≤3j}. 將項集中物品所有選擇情況記為矩陣A.則 (5) 定義1[9]假設問題包含n個項集,每個項集3個物品,則共包含3n個物品,每個項集對應的3個物品的價值系數為P=[P1,P2,…,Pn],質量系數為W=[W1,W2,…,Wn],每個項集對應的折扣率為D=[D1,D2,…,Dn].其中,Pi=[p3i-2,p3i-1,p3i],Wi=[w3i-2,w3i-1,w3i],Di=[d3i-2,d3i-1,d3i]. 給定背包的最大載重為C,為了避免所有解均為可行解,因此 (6) 則ESD{0-1}KP模型可描述如下: (7) (8) xi∈{0,1},i=1,2,…,n (9) 決策變量xi(1≤i≤3n)表示第i個物品是否被裝入背包.式(7)表示目標函數,即滿足約束條件下獲得收益最大.式(8)通過先求解第j個項集中物品經過折扣之后的值,再對所有項集的值進行求和.式(9)表示0-1約束. 與D{0-1}KP類似,ESD{0-1}KP通過在項集中增加物品以表示項集中多個物品同時被選擇的情況.因此,對于n個項集,且每個項集中有且僅有3個物品而言,一共有(23-1)n=7n種情況存在物品被選擇.記所有的物品選擇情況為矩陣R7n,3n={rij}7n,3n,且有 (10) Ri(1≤i≤7n)表示矩陣R的第i行,則第i行選擇情況的價值密度為 (11) 將物品序號按照計算完成后的價值密度從高到低的順序存儲在向量H中.也即對于?1≤i 結合公式(10),(11)以及文獻[9]提出GSOR,算法偽代碼描述見算法1. 算法1 GSOR 輸入:X 輸出:X 1.T1=X×PT;T2=0 2.FORi=1:n 4.END 5.FORi=1:7n 6.X′=sgn(X+RHi) 7.T3=X′×PT;T4=0 8. FORj=1:n 10. END 11. IFT4≤C 12. IFT3>T2 13.X=X′ 14. END 15. END 16.END 在算法GSOR中,步1計算原有決策變量的質量,時間復雜度為O(n).步2-4計算決策變量的質量,時間復雜度為O(n).步5-16進行GSOR貪心操作,時間復雜度為O(n2).其中,步6計算價值密度,步7計算貪心選擇的新決策變量的價值,步8-10計算新決策變量的質量,步11-15選擇滿足約束且價值更大的決策變量進行迭代.GSOR總的時間復雜度為O(n2). 當同一項集中兩種選擇情況沖突時,GSOR直接對兩種物品選擇情況取并集. 針對MCKP同一項集中多個物品同時被選擇的常見情況,IPA算法有非常良好的求解性能,且理論證明完善.與ESD{0-1}KP中“每個項集中至多選擇一項物品”約束不同,MCKP的約束為“每個項集中選擇且僅選擇一項物品”.顯然直接使用IPA并不可行,需要建立ESD{0-1}KP與MCKP的等價關系,再將IPA引入到ESD{0-1}KP的求解算法中,達到改進算法的目的. 為便于表述GSOR,將定義1中的ESD{0-1}KP 模型轉化為傳統的D{0-1}KP模型,模型可表述為 (12) (13) (14) yi∈{0,1},i=1,2,…,7n (15) 其中: p′i=Ri×PT (16) (17) 針對D{0-1}KP模型,每個項集中增加一個虛擬物品,其質量與價值均為0,價值密度為0.則模型可進一步轉化如下: (18) (19) (20) yi∈{0,1},i=1,2,…,8n (21) 顯然,公式(20)要求在每個項集中選擇且僅選擇一個方案,這類約束為多選擇約束.此時問題為MCKP模型,則使用IPA對同一項集中多個物體同時被選擇的情況進行求解.下面證明ESD{0-1}KP模型與MCKP模型等價. 值得注意的是,MCKP作為一個經典的NP問題,若項集中的物品價值與質量均相同,則問題退化為KP,因此,在MCKP的假設中任意項集不存在兩個物品的價值和質量均相等. 定理1若Y1滿足f1,g1,h1約束,Y2滿足f2,g2,h2約束.則Y1與Y2必然一一對應. 證對于Y1=[y11,y12,…,y1,7n],新增序號7n+1到8n共計n個物品,其物品價值與質量均為0,則有 因此,對于?Y1,必然存在Y2,使得 下證唯一性,利用反證法,假設?Y2≠Y3,且 綜上,結論成立. MCKP的相關內容可參考文獻[10-14]. 通過增加一個虛擬物品使得ESD{0-1}KP和MCKP在數學模型上完全一致,即傳統意義上求解MCKP的算法都能夠通過類似增加虛擬物品的操作,對ESD{0-1}KP和D{0-1}KP進行求解,豐富了ESD{0-1}KP和D{0-1}KP求解算法. 從定理1中不難發現,ESD{0-1}KP與MCKP是完全等價的,因此,對于求解MCKP問題的優秀算法也可以用于求解ESD{0-1}KP. ESD{0-1}KP可采用MCKP的貪心策略進行處理.同時,公式(18)-(21)模型仍存在傳統D{0-1}KP模型缺陷,即非正常個體編碼較多,可將MCKP中的貪心策略應用到ESD{0-1}KP模型中. 因IPA擁有計算速度快、求解精度高和算法結構簡單等特點,因此基于IPA提出適用于ESD{0-1}KP的NGSOR. 記第i個項集的所有物品為Ni,個數為n.第i個項集中所有的線性非支配(linear programming undominated,LP-undominated)物品集合稱線性非支配子集,并記為Li.由文獻[15]可知: 定理2[10]對于?s,t∈Ni,wis>wir,wit>wir,pit>pir,若eit>eis,且pit≥pis,則s?Li. 在式(18)-(21)模型中,結合定理2可知,wis>wir=0,wit>wir=0,pit>pir=0.對于同一項集中兩個物品s,t同時被選擇時,若eit>eis,且pit≥pis,則選擇物品t而不選擇物品s. 即對于ESD{0-1}KP,當按照選擇方案的價值密度從高到低選擇時,若同一項集中兩個選擇方案同時被選擇,應當選擇價值更大的選擇方案.由此得到NGSOR算法,算法偽代碼如下: 算法2NGSOR 輸入:X 輸出:X 1.FORi=1:n 2.Ps=[p3i-2,p3i-1,p3i-2+p3i-1,p3i,p3i-2+p3i,p3i-1+p3i,p3i-2+p3i-1+p3i] 3.Ws=[d3i-2w3i-2,d3i-2w3i-1,d3i-1(w3i-2+w3i-1),d3i-2w3i,d3i-1(w3i-2+w3i),d3i-1(w3i-1+w3i),d3i-2(w3i-2+w3i-1+w3i)] 4.P′=[P′,Ps];W′=[W′,Ws] 5.END 6.E=P′./W′;E=[E;1:7n] 7.E=-sortrows(-E′,1)′;H=E2 8.X=zeros(1,n) 9.FORi=1:7n 12.IFt2=0 13.e1=0 14.ELSE 15.t3=w′X3t1-2:3t1×[1,2,4]′+3t1-3;e1=t2/t3 16.END 17.t4=p′Hi;t5=w′Hi;e2=t4/t5 18.T=X;T3t1-2:3t1=AHi-7t1+7;Q=0 19.FORj=1:n 20. IF sum(T3j-2:3j)>0 21.Q=Q+w′T3j-2:3j×[1,2,4]′+7j-7 22. END 23.END 24.IFQ≤C 25. IFt2 26.X=T 27. END 28.END 29.END NGSOR與GSOR在時間復雜度上無數量級差異,但在GSOR中的步3與步9都需要重新計算每個項集選擇情況所對應的質量,而在NGSOR中則通過存儲后直接調用,因此NGSOR算法求解速度更快. 為充分展示NGSOR的算法性能,不僅與現有GSOR進行對比,同時與將文獻[9]貪心遺傳算法(greedy genetic algorithm,GGA)中的GSOR替換成NGSOR后得到的新型貪心遺傳算法(new greedy genetic algorithm,NGGA)進行對比.關于遺傳算法的相關內容可參考文獻[16-18]. 因NGGA僅將GGA中的貪心策略進行了修改,因此沿用文獻[9]中的參數算法設種群為50,最大迭代次數為100次,交叉概率pc=0.8,變異概率pm=0.01.此外,ESD{0-1}KP中,折扣系數為d3i-2=1,d3i-1=0.8,d3i=0.7. 測試數據集沿用文獻[9]中4類大規模實例,具體測試數據參數可參考文獻[9].其中,數據規模為300≤n≤3 000,且 1)EUDKP1-EUDKP10,參數設置wj∈z[2,1 000],pj∈z[2,1 000]. 2)EWDKP1-EWDKP10,參數設置wj∈z[101,1 000],pj∈z[wj-100,wj+100]. 3)ESDKP1-ESDKP10,參數設置wj∈z[2,1 000],pj∈wj+100. 4)EIDKP1-EIDKP10,參數設置pj∈z[2,1 000],wj∈pj+100. 其中z[a,b]表示在整數a到整數b之間的整數集. 文章使用計算機基本配置為:Intel Core i7-8700 CPU@3.2GHz(12 核),16GB DDR4L,Microsoft Windows 10家庭版.利用MATLAB R2016a對問題進行求解及繪圖. 利用NGSOR,GSOR,GGA和NGGA對4類數據進行求解.因NGSOR和GSOR算法為非隨機算法,因此僅參考最優值和求解時長指標.對于GGA和NGGA,因其為隨機算法,因此除了最優值和求解時長以外,還需要增加平均值和最差值指標. 為避免單次計算的偶然因素干擾,所有算法的求解時長為30次獨立求解均值.同時,為檢驗NGSOR的算法效果,對GGA重新進行測試. 算法計算結果見表1,其中折扣背包問題的動態規劃算法(dynamic programming of discounted knapsack problem,DPDKP)計算得到的結果為精確解. 表1 4類實例計算結果 由表1知,基于EUDKP算例,相比于GSOR的算法精度,NGSOR的誤差范圍從40.23%~50.54%縮小至3.97%~6.09%,對所有算例的提升精確度進行平均計算得到算法精度平均提升41.42%,同理得到算法速度平均提升40.68%.應用到遺傳算法中,NGGA相比于GGA,最優解精度平均提升33.22%,平均值精度平均提升34.42%. 基于EWDKP算例,相比于GSOR的算法精度,NGSOR的誤差范圍從10.32%~35.04%縮小至0.01%~0.22%,算法精度平均提升19.82%,同時算法速度平均提升45.85%.應用到遺傳算法中,NGGA相比于GGA,最優解精度平均提升15.18%,平均值精度平均提升16.07%. 基于ESDKP算例,相比于GSOR的算法精度,NGSOR的誤差范圍從12.98%~17.55%縮小至0.12%~0.41%,算法精度平均提升15.07%,同時算法速度平均提升44.31%.應用到遺傳算法中,NGGA相比于GGA,最優解精度平均提升15.08%,平均值精度平均提升15.07%. 基于EIDKP算例,相比于GSOR的算法精度,NGSOR的誤差范圍從18.70%~29.38%縮小至0.00%~0.06%,算法精度平均提升21.97%,同時算法速度平均提升48.94%.應用到遺傳算法中,NGGA相比于GGA,最優解精度平均提升14.56%,平均值精度平均提升15.96%. 整體分析,就算法精度討論,NGSOR平均誤差為1.31%,GSOR平均誤差為25.87%,平均提升24.56%.就算法速度而言,平均提升44.95%.總體上,NGSOR相對于GSOR具有明顯優勢,更加適應用于ESD{0-1}KP的求解,效果理想. 為了更好展示NGSOR性能,將表1數據繪制成圖1與圖2.從圖1中不難發現,NGSOR與NGGA求解效果均比GSOR和GGA效果更好.從圖2中可以知道,在求解時長方面,NGGA比GGA更快,且NGSOR也比GSOR更快. 圖1 最優解 圖2 求解時長 文章基于GSOR,通過改進模型,將ESD{0-1}KP與D{0-1}KP轉化為MCKP,再引入IPA對問題進行處理,算法性能提升明顯.值得注意的是,當ESD{0-1}KP的項集中物品數量繼續增加時,無論是NGSOR還是GSOR都需要指數級儲存空間,NGSOR雖然能夠提供更好的貪心結果,但其內存需求與GSOR并無特別大的改進.下一步工作,不妨思考新的支配關系與剪枝策略,提出更加優秀的貪心算法.2 傳統貪心策略算子
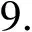
3 新型貪心策略算子
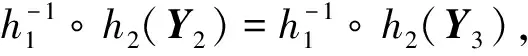
4 實例計算與結果對比
4.1 求解結果

4.2 結果分析

5 結束語

