促進學生理解的“生長式問題串”設計策略
——以“二次函數背景下的最值問題”專題復習課為例
彭文斌
(四川省成都七中八一學校 610036)
蘇聯著名教育家贊可夫曾說:“教會學生思考,這對學生來說,是一生中最有價值的本錢.”數學教學的本質是教學生學會思考,其核心是發展學生的思維能力,數學課堂要致力于讓學生思維真正發生.要到達這樣的目的,教師在教學中要設計富有情境的、有思考價值的問題,在層層遞進的生長式問題串驅動下,引領學生開展深度學習與深度思考,在這樣的狀態下獲得的知識是自然生長的、是終身的.
因此,在數學課堂中,教師要善于構建具有生長樣態的問題串,讓學生體驗數學發展的歷程,把握數學知識的本源,感受數學獨特的思維方式,在知識形成和解決問題的過程中,促進理解、融會貫通、靈活遷移,從而獲得智慧、提升數學素養.下面以“二次函數背景下的最值問題”專題復習課的教學設計為例,談談引領學生思維生長、促進學生理解的生長式問題串的設計策略.
1 確立核心問題,找準問題起點
“二次函數背景下的最值問題”這節專題復習課的核心問題是在二次函數背景下,動點引發的有關線段或面積最值問題的探究.在核心問題大背景下,努力找到探尋的起點,讓學生比較容易入手.故此,設置本節課第一個基礎的起點問題:
問題1拋物線y=-x2-2x+3位于x軸上方的圖象上有一動點P,點P距離x軸最遠時點P的位置在哪里?

圖1
這樣的問題讓學生很容易入手,發現距離x軸最遠的點是拋物線的頂點(圖1).問題1起點低,符合學生的已有知識基礎,這個問題成了后續所有問題的起點,我們就可以設置該問題的一系列變式問題.
2 明確生長點位,構建關聯變式
英國科學哲學家波普爾也曾說過:“科學和知識的增長永遠始于問題,終于問題——越來越深化的問題,越來越能啟發新問題的問題.”[1]在問題1的啟發下我們尋找關聯性極強的變式問題,探尋起點問題下的問題生長.因此,設計第二個引發深度思考的問題:

圖2
問題2已知拋物線y=-x2-2x+3與x軸交于點A,C,與y軸交于點B,點D(0,1),點P是位于第二象限拋物線上的動點,過點P作PH⊥x軸交線段CD于H,當PH取得最大值時,點P還是拋物線的頂點嗎(圖2)?
問題2與問題1關聯性極強,直線CD可以看作是將x軸繞著點C旋轉得到,但卻不能直接回答使得PH最大時點P是否還是拋物線頂點.從而引發學生深度思考與深入探究.
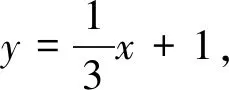
問題3已知拋物線y=-x2-2x+3與x軸交于點A,C,與y軸交于點B,點D(0,1),P是第二象限拋物線上的動點,當點P距離直線CD最遠時,求點P坐標(圖3).

圖3
問題3的提出是問題2的進一步探究,但學生想再直接建立點P到CD的距離PG的函數模型就更加困難了.解決這個問題讓學生進入深度思考,繼而想到平移直線CD與拋物線相切于第二象限,切點即為點P的位置.這一數形結合的方法自然而然地產生了.求切線和切點的方法背后的數形結合思想與方程思想可以讓學生徹底領悟數學之美.對于這些方法的普適性更應在教學中去滲透.問題3還可以如何生長?其實解答完問題3之后學生就會發現,問題3和問題2中的點P是同一點.由此生長出下一個問題:
問題4問題3中點P的位置與問題2中點P的位置是否相同?為什么?

圖4
問題4的提出讓學生尋求前兩個問題的關聯,從而對問題有更深入的認識:PG=PHcos∠HPG(∠HPG為定角,等于∠DCO),將求PG的最大值轉化為求PH的最大值(圖4).由此讓學生體悟數學的轉化思想,感悟數學的統一美.
3 遵循自然有道,把握生長方向
“最近發展區”理論告訴我們,學生認知的最大特性是“生長性”.如何讓學生在問題情境中自然而有力地獲得知識的生長,得到思維提升,享受數學學習的樂趣,體驗數學特有的魅力,激發自由創造的潛能,滋養數學內在的理性精神,需要教師的精鋪巧設與智慧引領.
在完成了問題2~4的探究之后,問題還有哪些值得挖掘、變式的地方應該往哪個方向去研究,需要教師精心設計問題變式.可考慮往三角形面積最值方面去變式,設計中提供以下三個問題,為后續研究提供參考:
問題5已知拋物線y=-x2-2x+3與x軸交于點A,C,與y軸交于點B,點D(0,1),P是第二象限拋物線上的動點,PG⊥CD,PH⊥x軸,當PG與PH取得最大時,△PHG的周長是否最大?此時△PHG的面積是否最大(圖4)?

圖5
問題6已知拋物線y= -x2-2x+3與x軸交于點A,C,與y軸交于點B,點D(0,1),P是第二象限拋物線上的動點,求△PCD面積的最大值,并求此時點P的坐標(圖5).
問題7△PCD面積取得最大值時,與問題2、問題3有沒有本質的區別?
問題5是問題4的延續,關聯性強,探究顯得自然流暢;問題6是問題5的進一步變式,將線段最值問題變式為與動點相關的三角形面積最值問題.前面問題的鋪墊,讓問題5~6的探究迎刃而解,一切的探究活動的開展都顯得自然有道.對其中的方法、思想、內涵,學生在回答完問題7后得到了認識上的升華,大大促進了學生對數學思想方法的理解和對問題本質的認識.
4 構建階梯變式,引領深度學習
問題情境設計注重層次性、遞進性、階梯性等基本原則,這同樣符合最近發展區理論.教師始終有意識地挖掘學生的認知需要與已有水平之間的矛盾,不斷地培養和激發學生的求知欲望,讓其始終處于“憤悱”狀態中.在探究完前七個關聯性很強的問題之后,課堂探究活動應該步入深層次學習.因此,考慮設計具有一定挑戰性的問題:

圖6
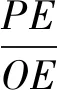
從問題1至問題8,始終遵循了問題變式的層次性和階梯性,遵循了問題發生的內在關聯,符合學生已有認知能力,滿足了學生求知的需求,引領著學生逐步進入深度思考、深度學習.在問題8探究結束后,設置了一個與此節課相關性極強的問題9(2020年成都中考試題):

圖7
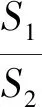
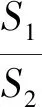
美國教育心理學家加涅曾指出“教學設計必須以幫助學習過程而不是教學過程為目的.”[2]讓“生成式問題串”引領、驅動課堂教學,只是教師優化教學設計的一種重要方式和途徑.在建構主義理論指引下,在生成性視野中,教學的過程是研究、傾聽、對話的過程.因此,在重視問題串設計的同時還要讓課堂教學實施走向民主化、開放化,重視對學生學習的關注、對過程的關注,培養學生發現問題、提出問題、分析問題、解決問題的能力.

