鋼-薄層UHPC 輕型組合橋面結構抗彎疲勞及剩余承載力試驗研究

曹君輝，趙宇航，邵旭東，沈秀將

［1.湖南大學土木工程學院，湖南長沙 410082；2.風工程與橋梁工程湖南省重點實驗室（湖南大學），湖南長沙 410082］

鋼橋的橋面主要采用正交異性鋼板，這種橋面板具有自重輕、承載力高、施工快捷等優點.但服役若干年后，鋼橋面系普遍存在兩大病害問題：一是鋼橋面板易疲勞開裂，二是橋面鋪裝頻繁破損.針對上述兩大病害問題，湖南大學邵旭東教授團隊［1］率先提出了鋼-薄層UHPC 輕型組合橋面結構（以下簡稱“輕型組合橋面結構”），即在傳統正交異性鋼橋面板上鋪設薄層UHPC（厚度一般為4.5～6 cm），進而顯著提高鋼橋面的局部抗彎剛度，大幅降低鋼橋面的疲勞應力幅，并改善磨耗層的受力狀態，能夠有效解決鋼橋面系的前述兩大病害難題.

鋼-薄層UHPC 輕型組合橋面結構具有優異的抗裂性能和抗疲勞性能.劉夢麟等［2］、丁楠等［3］制作了一個輕型組合橋面結構足尺條帶試驗模型，試驗分為三個階段：第一階段以距離左懸臂端1.7 m 為應力控制截面，UHPC 在拉應力幅為3.5～8.8 MPa 下進行200 萬次循環加載；第二階段以距離左懸臂端2.7 m 為應力控制截面，UHPC 在拉應力幅為7.01～14.42 MPa 下進行200 萬次循環加載；第三階段以距離右懸臂端1.7 m 為應力控制截面，UHPC 在拉應力幅為9.8～24.3 MPa 下進行310 萬次循環加載.三階段疲勞加載后U 肋與面板的連接焊縫處嚴重開裂，試驗終止，但此時UHPC 層仍然未出現疲勞裂縫.邵旭東等［4］探究了施工中行車擾動對輕型組合橋面結構抗裂性能的影響，結果表明，當擾動引起的UHPC拉應變不超過160 με 時，擾動不會顯著影響試件的抗裂性能.劉新華等［5］制作了3根不同負彎矩區接縫形式的鋼-UHPC 連續組合梁，發現試件的開裂強度均在20 MPa 以上，遠高于普通鋼-混凝土組合梁的開裂強度.Feng 等［6］研究了鋼筋間距對鋼-UHPC 組合梁抗彎疲勞性能的影響，當鋼筋間距為40 mm 時，UHPC 層在11.79 MPa 的等效應力幅下具有127.9×106次的預測疲勞壽命.

但目前在鋼-UHPC 輕型組合橋面結構的研究和應用中，栓釘間距多為150 mm，尚未系統探索不同栓釘間距對輕型組合橋面結構疲勞性能及剩余承載力的影響規律.清華大學劉誠等［7］設計了一組足尺模型試驗，研究了鋼-UHPC 組合橋面結構中栓釘的疲勞性能，其中栓釘間距為250 mm，栓釘剪應力幅達到119 MPa，經過200萬次加載循環后，試件仍未發生疲勞破壞現象；相關研究表明［8］，栓釘間距是影響鋼板-UHPC 界面滑移的重要因素，當鋼-UHPC 組合板栓釘間距從200 mm減小到150 mm時，靜力試驗中界面臨界滑移荷載增加了39.4%～182%，而失效時的最終滑移減小了81%～94%，但栓釘間距對輕型組合橋面結構的開裂荷載和極限承載力提升有限.

同時，在輕型組合橋面結構的負彎矩區，栓釘焊趾處的鋼面板處于復雜的拉應力-剪應力耦合疲勞狀態，目前對這一疲勞特性的研究甚少.曹君輝［9］雖然對薄層UHPC 中帶焊接栓釘的鋼板這一疲勞細節建立了熱點應力S-N曲線，但尚未進行疲勞試驗驗證.而對于常規鋼-混凝土組合結構中栓釘根部的鋼板這一疲勞細節，國內外學者開展了系列研究：清華大學聶建國院士團隊［10］對鋼板-混凝土組合加固梁試件開展了抗彎疲勞試驗，結果表明，試件的疲勞破壞均為受拉區鋼板疲勞斷裂，裂紋萌生于栓釘焊趾處的鋼板；Liu等［11］針對勁性鋼筋混凝土梁開展了靜力和疲勞試驗，結果表明，疲勞裂紋均萌生于H 形鋼梁外側受拉翼緣焊接栓釘焊趾處，裂紋沿翼緣高度和寬度方向發展，最終喪失承載能力；Kajikawa 和Maeda［12］對這一現象進行了深入研究，試驗結果表明，隨著栓釘剪應力幅增加，鋼板疲勞強度持續降低；方興等［13］給出了組合梁負彎矩區栓釘焊趾處鋼板疲勞評估的計算公式.

因此，本文將重點探明栓釘間距對鋼-UHPC 輕型組合橋面結構抗彎疲勞損傷特征的影響，并對栓釘焊趾處鋼面板的拉-剪耦合疲勞特性進行驗證，最后進行剩余承載力試驗，探明栓釘間距對疲勞損傷后UHPC抗裂性能及組合構件抗彎承載力的影響規律.

1 試件設計及制作

1.1 試件構造

本文試驗設計為含U形加勁肋的鋼-薄層UHPC輕型組合條帶模型，共制作了3 個試件，試件尺寸如圖1 所示.各個試件僅栓釘間距不同，其余尺寸均相同，試件采用Q345qD 鋼板，鋼面板上焊接直徑為13 mm的栓釘，焊后高度32 mm.UHPC層厚45 mm，其內配筋采用HRB400 帶肋鋼筋，鋼筋直徑為10 mm，其中橫向鋼筋置于縱向鋼筋上側，橫向鋼筋的凈保護層厚度為15 mm.

圖1 試件構造和尺寸（單位：mm）Fig.1 Configuration and dimension of specimens（unit：mm）

試件中采用的UHPC 主要由水泥、硅灰、粉煤灰、石英砂、石英粉、高效減水劑、平直型鋼纖維和水等組成，各組分相對用量見表1.其中，鋼纖維包含?0.12 mm×8 mm（體積摻量1.5%）和?0.2 mm×13 mm（體積摻量2.0%）兩種，總體積摻量3.5%.

表1 UHPC配合比（質量比）Tab.1 Matrix composition of UHPC（mass ratios）

試件制作的主要過程如下：鋼梁加工、焊接栓釘、綁扎鋼筋、支模、澆筑UHPC、蒸汽養護.UHPC 澆筑完成后覆膜灑水，3 d 后開始蒸汽養護，養護溫度控制在90～100 ℃，持續48 h.試件的主要制作工序如圖2所示.

圖2 試件制作主要步驟Fig.2 Fabrication procedures of specimens

試件制作過程中，同步澆筑了一批UHPC 材料性能測試試件，包括：100 mm×100 mm×100 mm 抗壓試件、100 mm×100 mm×300 mm 彈性模量測試試件以及100 mm×100 mm×400 mm 抗折強度測試試件各6個，按《活性粉末混凝土》（GB/T 31387—2015）［14］中的材料性能標準測試方法進行試驗.同時，制作了6個狗骨形試件開展UHPC 直接拉伸試驗［15］.對各材性實測結果取平均值，得到UHPC 的力學性能參數，如表2所示.

表2 UHPC力學性能Tab.2 Mechanical properties of UHPC

1.2 試驗參數及測點布置

如上文所述，本試驗的主要目的為：1）疲勞試驗中，掌握栓釘間距對鋼-UHPC 輕型組合橋面結構疲勞損傷特性的影響規律，并探明鋼面板在拉-剪耦合疲勞受力下的狀態；2）剩余承載力試驗中，探明栓釘間距對經歷疲勞損傷后UHPC 層的裂縫發展特性和試件剩余承載力的影響規律.

以栓釘間距作為主要試驗參數，試件S100、S150和S300的栓釘間距分別為100 mm、150 mm、300 mm.同時，根據材料力學理論，各試件中的栓釘名義剪應力幅和鋼板正應力幅不同，通過改變荷載幅來控制試件的應力水平.

試驗中栓釘的名義剪應力幅按公式（1）計算；計算簡圖如圖3 所示，其中beq為UHPC 板換算寬度，取beq=147.9 mm.

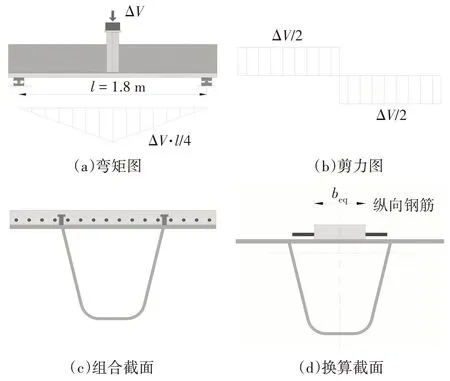
圖3 名義剪應力計算簡圖Fig.3 Calculation diagrams of nominal shear stress

式中：d為栓釘縱向間距；n為栓釘列數；Asd為栓釘的截面面積；ΔV為剪跨段的剪力幅；I0為組合截面的換算截面慣性矩，即按模量等效將UHPC 層換算成鋼板，再求得組合截面的慣性矩，取I0=1.89×108mm4；Q為換算截面中鋼面板與UHPC 交界面以上截面的一次矩，取Q=4.3×105mm3.

根據公式（1）和本文試驗思路，得到各試件的試驗方案具體參數如表3所示.

表3 試驗加載參數Tab.3 Parameters in the fatigue test

疲勞試驗采用電液脈動全自動試驗機進行加載，加載頻率控制為4 Hz，應變由東華D3816N 型靜態應力應變測試分析系統采集，UHPC與鋼面板之間的滑移以及支座與跨中的撓度均使用千分表測得，精度為0.001 mm.試件加載裝置及主要測點布置分別如圖4和圖5所示，試驗加載照片如圖6所示.

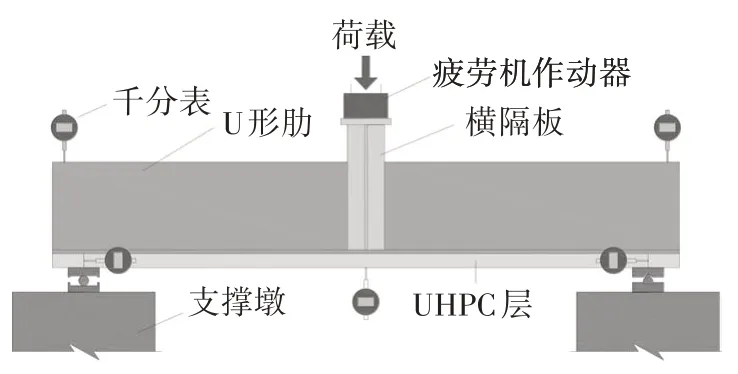
圖4 試驗加載裝置Fig.4 Test setup

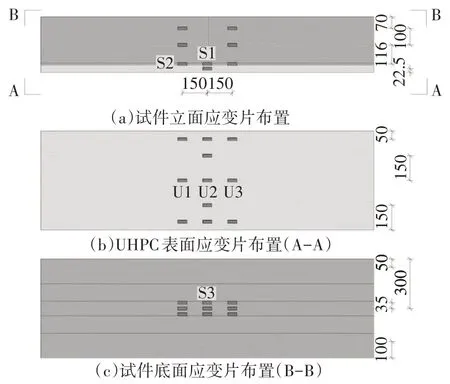
圖5 試驗測點布置圖（單位：mm）Fig.5 Layout of strain gauges（unit：mm）

圖6 疲勞試驗加載照片Fig.6 Photo of the fatigue test

2 疲勞試驗及結果分析

2.1 疲勞現象及破壞形態

根據上文確定的試驗方案和加載思路，所有試件首先進行疲勞加載，若試件未疲勞破壞，則進行剩余承載力試驗.試驗結果表明，試件S100 在鋼面板-U 肋間的焊縫處發生了疲勞破壞，而其他兩個試件雖然出現了疲勞裂紋，但并未破壞，具體如下.

3個試件均出現了疲勞裂紋，疲勞開裂照片如圖7（a）所示，即U 肋與橫隔板相交的焊縫處出現了疲勞裂紋.下面對試件在該位置的疲勞開裂情況進行簡要分析和討論.

圖7 疲勞破壞形態Fig.7 Fatigue crack and failure pattern

S100 加載至350 萬次出現初始疲勞裂紋，S150加載至400 萬次時出現疲勞裂紋，而S300 在疲勞加載末期（3 200 萬次）才出現疲勞裂紋.根據《公路鋼結構橋梁設計規范》（JTG D64—2015）［17］，取該疲勞細節的S-N曲線斜率m=3，200 萬次壽命對應的疲勞強度為80 MPa.因此，基于Miner線性損傷累計準則，并根據表1 的荷載參數，可將各試件的變幅疲勞次數換算為80 MPa 應力幅下的等效循環次數.計算結果表明，S100、S150、S300 萌生疲勞裂紋時的等效循環次數分別為246 萬次、462 萬次、547.3 萬次，均超過了前述規范規定的200萬次抗疲勞要求.

此外，對于試件S100，當加載至420萬次時，U肋與鋼面板的焊縫處發生了開裂，隨后焊縫逐漸脫開，如圖7（b）所示.該試件U 肋與鋼面板焊縫脫開后，引起試件破壞，因而未進入剩余承載力試驗階段.

2.2 不同循環次數下UHPC頂面裂縫分布

試驗中采用智博聯F130 型裂縫寬度觀測儀讀取UHPC 表面及側面的裂縫寬度.由于3個試件的裂縫發展過程相似，故本節以試件S150為例，闡述UHPC裂紋的發展階段及特征，圖8為該試件在疲勞加載階段及剩余承載力試驗階段的UHPC裂縫分布示意圖.

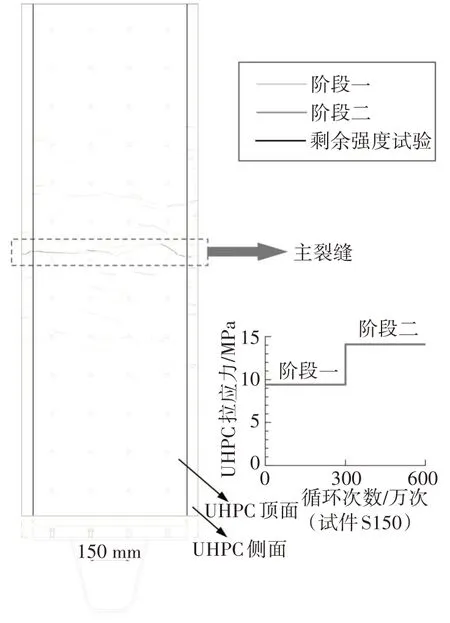
圖8 試件S150裂縫分布圖Fig.8 Crack distribution on surface of the UHPC layer in specimen S150

下面分階段闡述裂縫的萌生與發展過程.

階段一：試件S150 表面的裂縫呈現“短而密”的特點.初次加載時該試件共產生4 條裂縫，最大裂縫寬度0.026 mm，裂縫均出現在UHPC 層側面，未延伸至底面，分析其原因可能與實驗室模型制作有關，模型中橫向鋼筋距UHPC 層側面距離的設計值僅10 mm，而模型在實驗室的加工可能存在一定偏差，導致該位置較為薄弱，進而在UHPC 側面產生初始裂縫.當疲勞荷載加載到10 萬次時，共產生8 條裂縫；加載至50萬次時共產生15條裂縫；之后繼續加載至200 萬次，裂縫數量沒有增加，裂縫寬度基本保持不變，跨中附近裂縫向底面延伸.加載至300 萬次時增大應力幅，試件裂縫密集開展，裂縫數量增至32 條，而跨中裂縫長度并未增加，最大裂縫寬度增大至0.13 mm，裂縫在跨中主裂縫附近密集開展.

階段二：加載至500 萬次時，裂縫寬度增大到0.135 mm，加載至600 萬次時，裂縫寬度增至0.155 mm，裂縫寬度增長速率加快，試件S150 側面裂縫與底面裂縫有貫通趨勢，跨中附近截面裂縫增生.

圖9 繪制了各試件UHPC 層最大裂縫寬度隨疲勞加載次數的變化.由該圖可以看出，各加載階段UHPC 層的裂縫發展基本穩定，其中，由于試件S300中的UHPC 層總體處于較低的拉應力水平，加載至3 000 萬次時，其最大裂縫寬度僅約為0.02 mm，相比之下，試件S100 和S150 的UHPC 層拉應力更高，在第二階段下疲勞裂縫擴展較快.此外，對比S100 和S150 在第二階段的加載過程，S150 中UHPC 裂縫寬度更大，分析其原因為：試件S100 中栓釘間距更小，進一步約束了UHPC中疲勞裂縫的發展.

圖9 UHPC表面最大裂縫寬度發展規律Fig.9 The development of maximum crack width in UHPC during the fatigue test

2.3 荷載-UHPC應變特征

疲勞加載過程中持續觀測了UHPC 頂面的應變變化，每次疲勞停機后進行靜力單調加載，各試件的荷載-UHPC 應變變化規律如圖10 所示，應變片具體位置可見U2（圖5）.由該圖可看出，總體而言，隨著疲勞加載次數的增加，各加載階段UHPC 的拉應變呈現出增大的趨勢.此外，當荷載上限低于初裂荷載時，UHPC 應變隨循環次數增加緩慢增長.而當荷載提高進入下一疲勞加載階段時，若單調加載過程中試件UHPC 表面開裂（即超過初裂荷載），卸載后再次加載，則荷載-應變曲線斜率呈現增大趨勢.朱忠等［18］開展的試驗同樣發現類似規律，分析其原因為測點附近截面出現了細微裂縫，應變能得到釋放，導致該裂紋附近的其他測點處應變沒有增加反而略有減小.

圖10 跨中UHPC層表面荷載-應變曲線隨疲勞加載次數的變化規律Fig.10 Load-strain curves on surface of the UHPC layer in mid-span during the fatigue test

圖11 繪制了初次加載（即疲勞加載之前），當荷載為100 kN 時，各試件UHPC 表面應變試驗值與理論計算值沿試件縱向的分布.此時所有試件均未開裂，支座處應變假設為0 με，應變片的具體位置可見U1～U3（圖5）.可以看出，隨著栓釘間距的增大，相同荷載下UHPC 縱向應變減小，這是由于鋼梁與混凝土翼緣交界面的滑移效應所致，滑移效應使得鋼梁截面壓應力的合力位置下移（向U 肋受壓底板方向移動），截面拉應力合力和壓應力合力之間的力臂增大，在彎矩不變的情況下，需要與鋼梁壓力平衡的UHPC層拉力減小［19］，故UHPC層應變減小.

圖11 UHPC表面應變沿縱向分布Fig.11 Longitudinal strain distribution on the surface of the UHPC layer

同時，對于橫隔板頂面位置，試件S100 和S150應變的試驗值明顯高于理論值，而試件S300 應變試驗值小于理論值.在試件跨中橫隔板上方位置，S300沒有布置栓釘，而其余兩個試件在該位置布置了栓釘.因此，分析引起上述受力特點的原因為：橫隔板頂面布置栓釘將導致該位置UHPC 層出現應力集中，因而實橋設計中栓釘的布置應避開橫隔板頂面位置.

2.4 荷載-鋼板應變特征

由于栓釘焊趾位置的鋼板存在應力集中，難以直接測量該位置的鋼板應變.汪爾穎［20］嘗試了在焊接栓釘位置的鋼板底部粘貼應變片，但本試驗鋼面板下方焊有U 形肋，不易粘貼應變片.因此，為探究栓釘位置鋼面板的應變變化規律，選取距跨中最近的焊栓釘截面位置，提取該截面處鋼面板側面的應變，以表征其發展特點，如圖12 所示，應變片具體位置可見S2（圖5）.

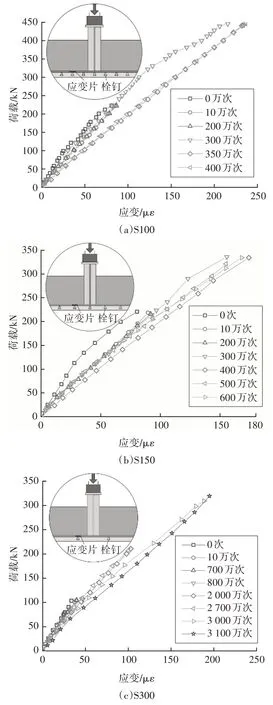
圖12 鋼面板荷載-應變曲線隨疲勞加載次數的變化規律Fig.12 Load-strain curves on side surfaces of the steel deck plate during the fatigue test

由圖12 可以看出，由于該位置距離中性軸較近，應變水平不高，使得應變結果表現出一定的波動性，但總體而言，隨著疲勞加載次數的增加，鋼面板的拉應變呈現一定的增大趨勢.

同時，選取試件跨中U 肋受壓區底板應變數據進行分析，如圖13 所示，其中應變片的具體位置可見S3（圖5）.試件S300 的U 肋受壓區應變呈現微小的增大趨勢，試件S100 與S150 鋼板壓應變相對穩定，整個循環加載過程幾乎不變，分析其原因為：該位置距離組合梁中性軸較遠，UHPC開裂后引起的中性軸位置變化對該位置應變的影響較小，因此，U 肋底面應變在疲勞加載過程中始終較為穩定.

圖13 U肋受壓底板應變曲線隨疲勞加載次數的變化規律Fig.13 Load-compressive strain curves at the bottom of U rib during the fatigue test

2.5 荷載-滑移曲線

試驗中關注了鋼-UHPC 界面滑移隨疲勞加載的發展規律，如圖14 所示.圖中，橫軸為疲勞循環加載次數，縱軸為鋼-UHPC 相對滑移與梁跨中荷載之比Se［式（2）］，以反映單位荷載所引起試件的界面滑移量.

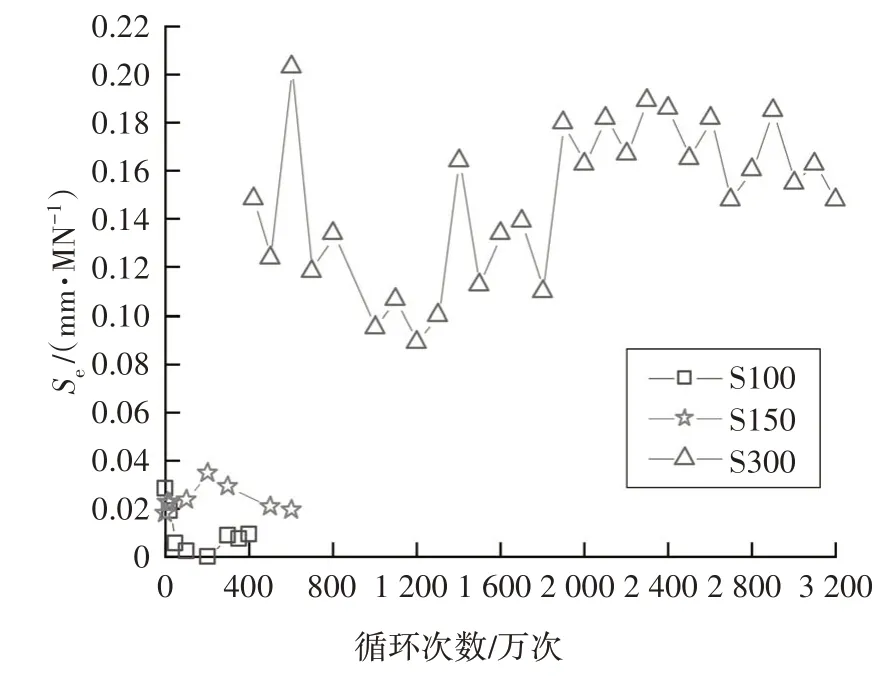
圖14 疲勞過程UHPC與鋼面板間相對滑移Fig.14 Relative slip caused by uniform load between UHPC and steel deck plate in the fatigue test

式中：ΔS為疲勞試驗過程中，最大靜力荷載下鋼-UHPC 界面的滑移量，mm；P為疲勞試驗過程中，停機時的最大靜力荷載，kN.

由圖14 可以看出，當栓釘間距為100 mm 和150 mm 時，相對滑移量很小，而當栓釘間距增大到300 mm 時，相對滑移量明顯更高，說明栓釘間距對試件的靜力滑移特性有較大影響.但整個加載過程中，各試件中單位荷載引起的滑移量基本保持穩定，表明在疲勞加載過程中，界面栓釘的剛度衰減和滑移增長并不明顯.

同時，本試驗測試過程中由于鋼-UHPC 界面黏結機理復雜，滑移數據存在一定的波動.分析其原因可能是界面摩擦力對滑移量影響較大，李嘉等［21］使用動位移傳感器連續記錄了加載次數對應的滑移量，結果表明鋼板與UHPC 之間的黏結效應對試件的抗剪疲勞性能影響較大，該文獻的疲勞試驗中同樣具有類似的滑移數據波動現象.

3 短栓釘處鋼面板的拉-剪耦合疲勞狀態分析

本文疲勞試驗采用負彎矩加載模式，導致栓釘根部的鋼面板處于復雜的拉-剪耦合疲勞狀態，圖15示意了栓釘位置鋼板及栓釘的受力狀態.

對于鋼-UHPC 輕型組合橋面結構的上述疲勞細節，目前尚未形成適宜的疲勞設計方法.而對于普通鋼-混凝土組合結構橋梁，我國《公路鋼混組合橋梁設計與施工規范》（JTG/T D64-01―2015）［22］中考慮了負彎矩區鋼梁上翼緣板承受拉應力幅且同時承受栓釘根部剪應力幅的耦合作用，規范中采用公式（3）～公式（5）進行疲勞驗算.

式中：γMf為疲勞抗力分項系數，取1.15；γMf，s為剪力連接件疲勞抗力分項系數，取1.0；γFf為疲勞荷載分項系數，取1.0；Δσc、Δτc為對應于2.0×106次常幅疲勞循環的疲勞應力強度，即鋼材疲勞抗力，Δσc取80 MPa，Δτc取90 MPa；ΔσE，2、ΔτE，2分別為變幅疲勞應力幅換算成200萬次疲勞循環對應的正應力幅和剪應力幅.

根據相關規范推薦的S-N曲線進行疲勞評估時，一般僅考慮單向應力因素，而本文應考慮雙應力耦合作用對栓釘位置鋼面板進行疲勞驗算，具體計算思路如下：

首先對栓釘剪應力幅和鋼板拉應力幅分別進行了應力幅等效，即將試驗中的變幅疲勞應力幅和加載次數，根據各自的疲勞S-N曲線（圖16）按Miner線性累計損傷原則換算到200 萬次疲勞循環對應的等效應力幅，換言之，等效前后的疲勞損傷相同，具體換算過程按照公式（6）和（7）進行.然后將得到的栓釘等效剪應力幅和鋼板拉應力幅繪制到圖17中，并與《公路鋼混組合橋梁設計與施工規范》（JJG/T D64-01—2015）中的公式［即公式（3）～（5）］進行對比，以分析本文試驗中鋼面板的拉-剪耦合疲勞狀態.

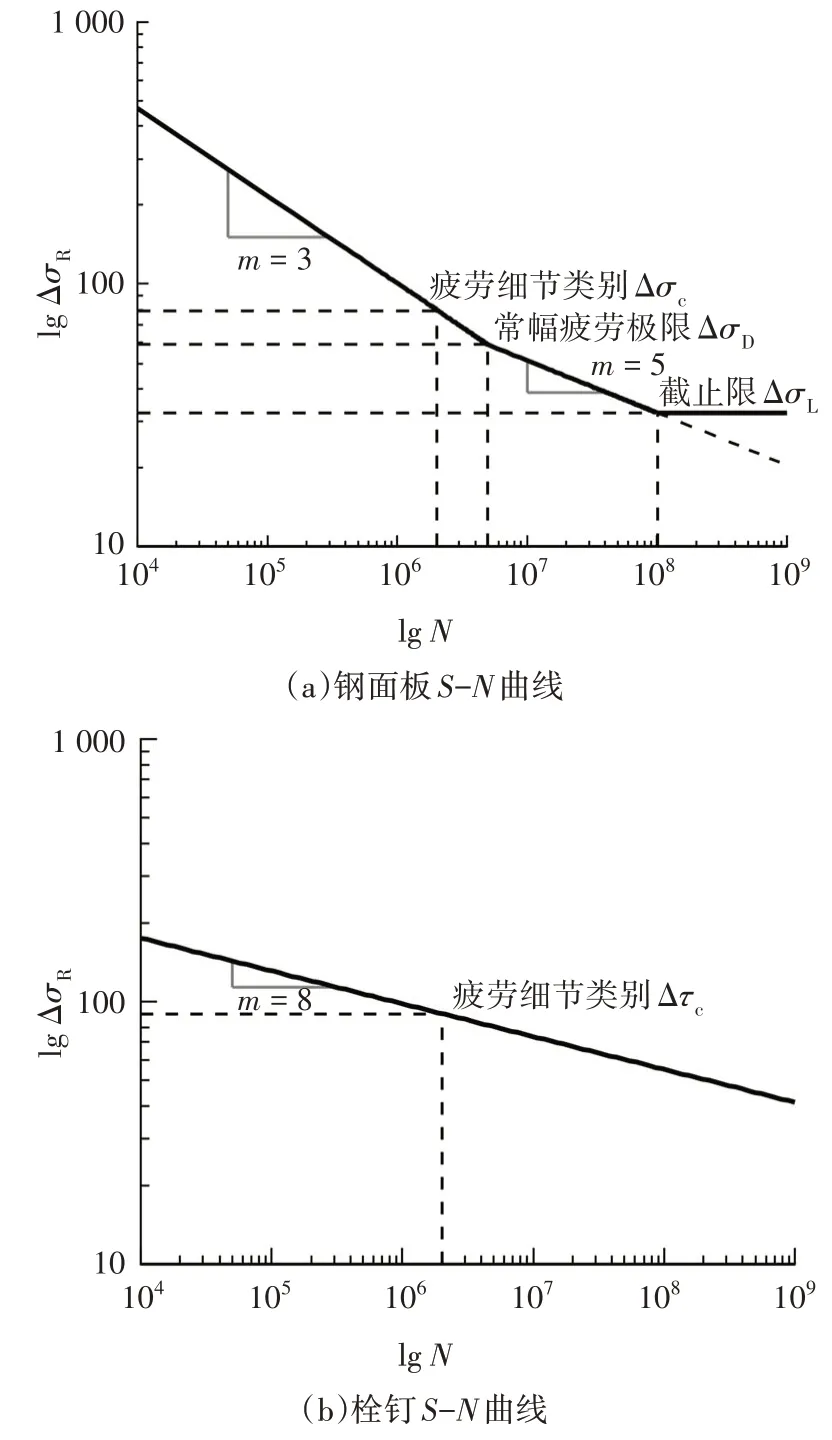
圖16 鋼面板和栓釘的S-N曲線Fig.16 S-N curves for steel deck plate and headed stud

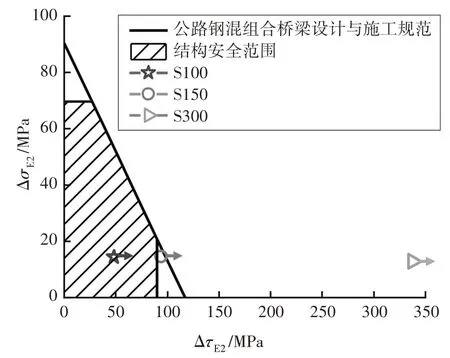
圖17 栓釘根部鋼面板拉-剪耦合效應驗證Fig.17 Verification of the test results with fatigue strength under combined action of tension and shear stresses

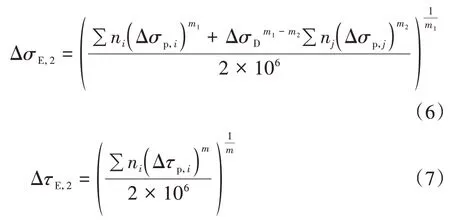
式中：ΔσE，2、ΔτE，2分別為200 萬次循環下的等效常幅疲勞正應力幅和剪應力幅；Δσp，i、ni、Δσp，j、nj分別為m1=3 和m2=5 直線段范圍內的正應力幅和對應的循環次數；Δτp，i、ni為栓釘剪應力幅計算時，m=8 直線段范圍內的剪應力幅和對應的循環次數.

需要說明的是，計算鋼面板等效正應力幅ΔσE，2時，根據我國《公路鋼結構橋梁設計規范》，當Δσp，i大于常幅疲勞極限ΔσD時，m=3；當Δσp，i小于ΔσD而大于疲勞截止限ΔσL時，m=5；當Δσp，i小于ΔσL時，規范不計入此部分應力幅的影響.本文計算中，雖然試件鋼面板正應力幅均低于疲勞細節對應的ΔσL（32.4 MPa）［17］，但仍偏保守地認為這些低應力循環仍會在鋼板中引起疲勞損傷，因而仍對低于ΔσL的應力幅進行換算.

因此，利用鋼面板S-N曲線［圖16（a）］計算試件鋼面板等效正應力幅ΔσE，2.根據吳沖等［23］推薦的公式［式（6）］，將S-N曲線中m=5 對應的直線段延長［圖16（a）］，以計入低應力幅對結構疲勞損傷的影響.同時，在利用栓釘抗剪S-N曲線［圖16（b）］計算ΔτE，2時，由于曲線為單一斜率，故對試件栓釘所有加載階段均按m=8進行換算.

基于上述計算思路，分別對3 個試件進行疲勞等效計算，得到試件對應200 萬次疲勞循環對應的等效疲勞應力幅，其中鋼面板正應力幅和栓釘剪應力幅分別記為ΔσE，2和ΔτE，2，計算結果如表4所示.

如圖17所示，圖中列出表4中的試件應力幅，其中的水平箭頭表示試件在疲勞加載中在栓釘根部的鋼面板位置未出現拉-剪耦合疲勞破壞.雖然本文的試驗樣本數量有限，但根據該圖仍可判斷，即使等效疲勞應力幅在規范規定的拉-剪耦合疲勞曲線之外，也沒有在該疲勞細節出現疲勞破壞現象，表明按公式（3）～（5）方法驗算鋼-UHPC 輕型組合結構中鋼面板的拉-剪耦合疲勞能夠獲得偏保守的結果.因此，考慮到目前沒有更多輕型組合橋面結構中鋼面板拉-剪耦合疲勞試驗數據，可偏保守地參考規范［22］的計算公式［即本文公式（3）～（5）］進行輕型組合橋面結構中鋼面板拉-剪耦合疲勞驗算，結果偏于安全.

表4 等效應力幅計算結果Tab.4 Calculation results of the equivalent stress range

4 剩余承載力試驗及分析

4.1 試驗加載過程

疲勞加載結束后，對未發生疲勞破壞的試件（S150 和S300）進行了剩余承載力試驗，試驗中采用千斤頂加載，直至試件破壞.剩余承載力試驗中的測試內容與疲勞加載階段基本相同，詳細可參考圖5中的測點布置.

4.2 試驗現象和破壞模式

試件破壞前大致經歷了3 個階段，即彈性階段、裂縫發展階段和屈服階段.在彈性階段，試件未產生新的裂縫；在裂縫擴展階段，雖然有裂縫產生，但是構件剛度未出現明顯折減；進入屈服階段，隨著荷載的緩慢增加，撓度快速增長，達到極限承載力后，試件依然表現出良好的延性特征，最后進行卸載.圖18展示了試件剩余承載力試驗的破壞形態.

圖18 試件破壞模式（S150與S300）Fig.18 Failure pattern of the specimen（S150 and S300）

試件S150 與S300 的破壞過程主要包括兩個方面：一是在疲勞加載階段產生的橫隔板與U 肋焊縫位置的疲勞裂縫，該裂縫在剩余承載力試驗階段持續增長，且U 肋屈服后迅速擴展；二是試件達到極限荷載后，U 肋壓屈，隨后試件荷載開始逐漸進入下降段.整個加載過程除UHPC 層鋼纖維拔出產生“滋滋”的響聲外，未發生突然破壞現象.

4.3 荷載-撓度曲線

試驗中得到了試件的荷載-撓度曲線及彎矩-撓度曲線，如圖19所示，具體特征如下：

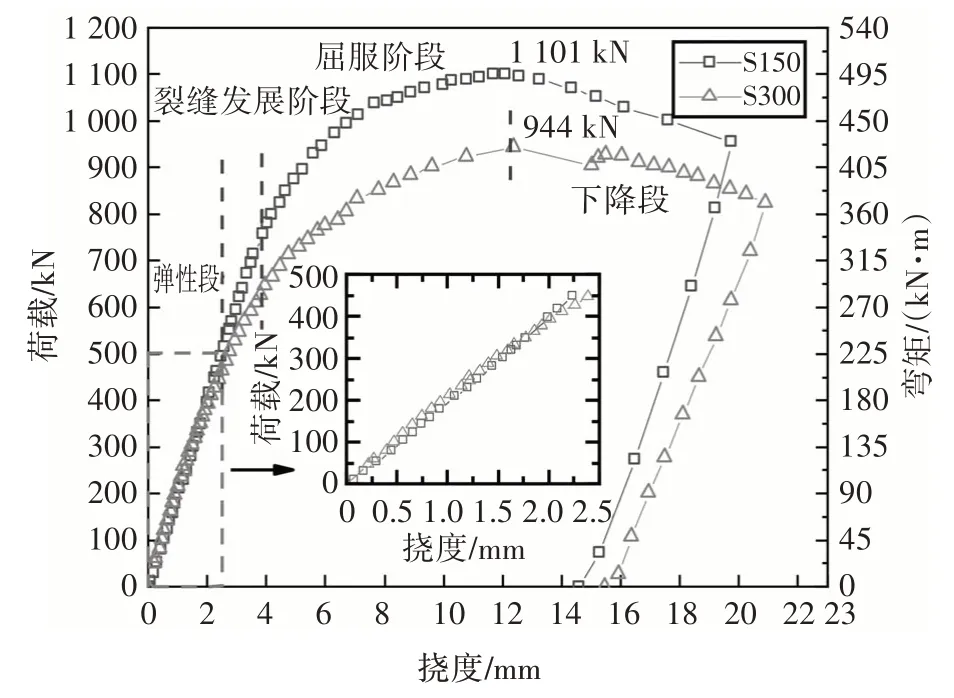
圖19 荷載-跨中撓度曲線Fig.19 Curves representing relationship between load（or moment）and mid-span deflection

1）在彈性階段，曲線呈線性變化，UHPC 除在疲勞階段產生的裂縫外，未產生新的裂縫，試件S150與S300線性段大致重合；

2）進入裂縫發展階段后，荷載分別增至極限荷載的65%、62%時，試件S150 與S300 跨中U 肋底板進入屈服狀態，U 肋受壓區底板應變迅速增長，鋼板進入強化段；

3）試件分別在1 101 kN（S150）和944 kN（S300）達到極限狀態，隨后曲線進入下降段，試件仍可穩定持荷，試件表現出良好的延性.

上述試驗現象及結果表明，疲勞加載過程對試件的破壞形態并無明顯影響，試件到達極限荷載后仍具有良好的延性.羅軍［8］對類似的鋼-UHPC 組合梁試件直接進行了靜力破壞試驗（即未進行疲勞加載），本文試件與該文獻報道的破壞模式大體類似，均表現為3 階段破壞.對比表明，雖然本文試件經歷了疲勞加載，但仍具有良好的剩余承載性能.

4.4 彎矩-最大裂縫寬度曲線

試驗中測得了UHPC 層最大裂縫寬度隨試件跨中彎矩的變化規律，如圖20所示.試件中UHPC層最大裂縫均位于跨中橫隔板下方兩側底面靠近側面的位置.每個試件跨中兩側各存在一條裂縫，圖中包含S150和S300兩個試件，共計4條裂縫.

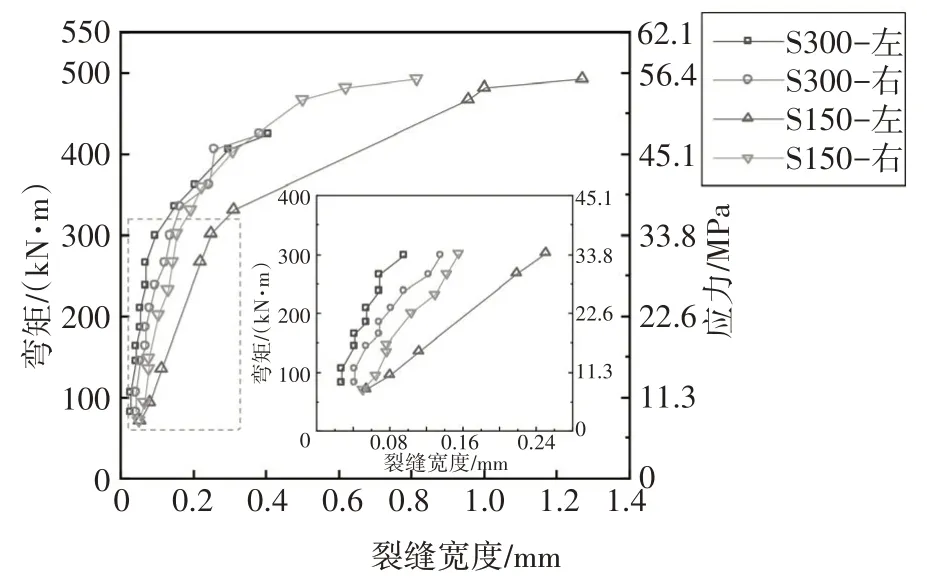
圖20 彎矩及應力與UHPC最大裂縫寬度關系曲線Fig.20 Curves representing relationship between moment and maximum crack width of UHPC

由圖20 中可以看出，在剩余承載力試驗加載前期，S150 和S300 試件的裂縫寬度基本呈線性增長，試件S300 加載至311 kN 時，最大裂縫寬度達到0.05 mm，此裂縫為疲勞加載階段已經出現的裂縫.S300加載至448 kN時，繼疲勞加載后萌生一條新裂縫；而對于試件S150，加載至160 kN 時，最大裂縫寬度達到0.05 mm，S150 加載至495 kN 時，繼疲勞加載后萌生一條新裂縫.

進入屈服階段后，鋼纖維的橋接作用使得UHPC層并未退出工作，UHPC 裂縫寬度增長速度加快.試驗中UHPC 層的最大裂縫位置均出現在跨中橫隔板下方，且該位置在疲勞循環加載階段已經產生裂縫.

此外，在圖20 的線性階段，相同荷載下試件S150 的裂縫寬度比S300 要大，這是由于疲勞加載階段試件S150 的荷載幅更大、UHPC 層的拉應力更高，導致疲勞試驗中該試件UHPC 層已經出現了較寬的疲勞裂縫（圖9），因此，在剩余承載力試驗階段，疲勞裂縫重新張開，進而導致裂縫發展較快.

下面進行疲勞加載過程名義開裂強度的對比，在疲勞試驗過程中，當停機進行靜載試驗且UHPC最大裂縫寬度為0.05 mm時，定義對應的荷載為開裂荷載，然后根據材料力學理論計算對應的名義開裂應力.對于試件S150，加載300 萬次后名義開裂強度為13.1 MPa.對于試件S300，由于UHPC 的拉應力水平始終較低，加載至3 000 萬次時最大裂縫寬度僅0.02 mm，加載3 200 萬次后最大裂縫寬度達到0.05 mm，對應的名義開裂強度為15.7 MPa，對比S150 和S300，疲勞加載結束后S300 的名義開裂強度高于S150，這是由于S150 應力水平較高，疲勞損傷較S300更高，因而其名義開裂強度低于S300.

4.5 荷載-滑移曲線

本試驗選取試件4 個角點位置記錄滑移數據，模型中4 個角點位置對稱；使用千分表采集數據并取平均值作為最終滑移，如圖21所示.

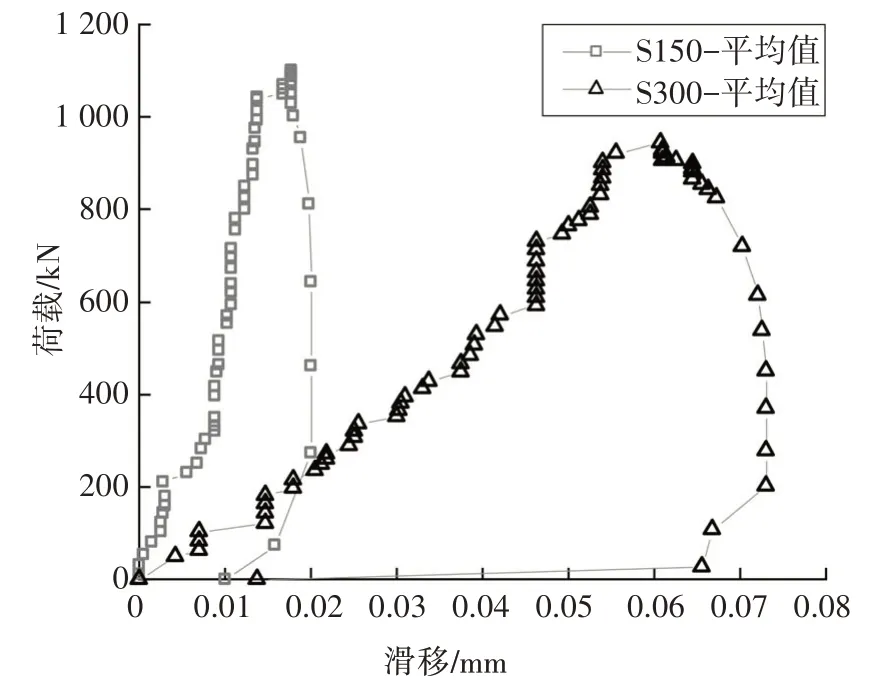
圖21 荷載-界面滑移曲線Fig.21 Load-interfacial slip curves

由圖21 可以看出，當荷載較小時，隨著荷載增大，試件S300 比試件S150 滑移增長更為迅速.達到極限荷載時，試件S150 平均滑移0.018 mm.參考羅軍［8］類似試件的靜力試驗結果，當栓釘間距為155 mm時，極限荷載時的滑移約為0.02 mm，與本文結果非常接近.本文試件S300 的平均極限滑移為0.061 mm，因此，栓釘間距由150 mm 增加到300 mm 時，達到極限荷載時的最終滑移增加了238.9%.

因此，滑移測試結果表明，栓釘間距會顯著影響鋼-UHPC 組合梁的抗滑移靜力性能，隨著栓釘間距增大，試件破壞時滑移將大幅增加.

4.6 荷載-鋼板應變特征

圖22繪制了跨中U肋受壓區底板應變隨加載過程的變化.可以看出，在線性段，曲線的斜率大體相同；達到極限荷載后繼續加載，鋼板應變仍然穩定，U肋壓屈后仍可繼續持荷.荷載分別增至極限荷載的62%（試件S300，591 kN）、65%（試件S150，715 kN）時，跨中U肋底板逐漸進入屈服狀態.

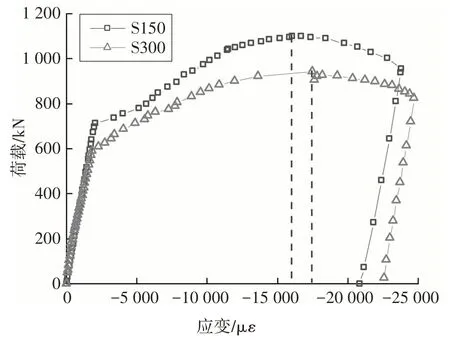
圖22 跨中U肋受壓區底板應變（S3）Fig.22 Load-compressive strain curves at the bottom of the U-shape rib in mid-span（S3）

圖23 則繪制了跨中鋼面板側面的應變，加載前期，試件S150 應變較試件S300 大，表明試件S150 中性軸更靠近U 肋底面，而前文疲勞加載階段S150 的UHPC 應變較S300應變大，規律一致.當達到極限荷載時，鋼面板并未屈服，但此時U 肋已經屈服，試件已經無法繼續加載.超過極限荷載后，可以看出U 肋底面應變急劇增大，而鋼面板應變卻基本不變，U 肋底面鋼板達到極限應變后進入應力軟化段，此時荷載不升反降，荷載已經無法繼續增加.

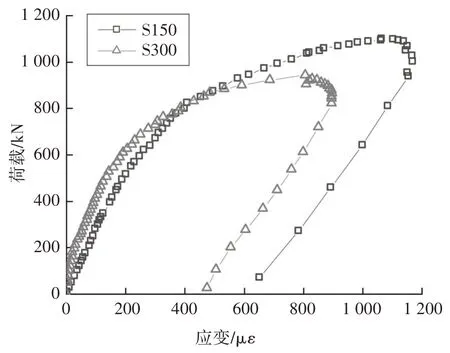
圖23 跨中鋼面板側面應變Fig.23 Load-strain curves on the sides of the flange of U-shape rib in mid-span

4.7 剩余抗彎承載力計算理論

本節分別基于組合結構橋梁的彈塑性和塑性計算理論，計算了負彎矩作用下鋼-UHPC 組合梁的剩余抗彎承載力，其中，UHPC 層考慮了其裂后抗拉貢獻.鋼材的抗壓強度高于屈服強度（345 MPa），為簡化計算，當U 肋受壓區應變超過屈服應變后，假設鋼材屈服后始終保持強度不變，材料的本構關系如圖24所示.

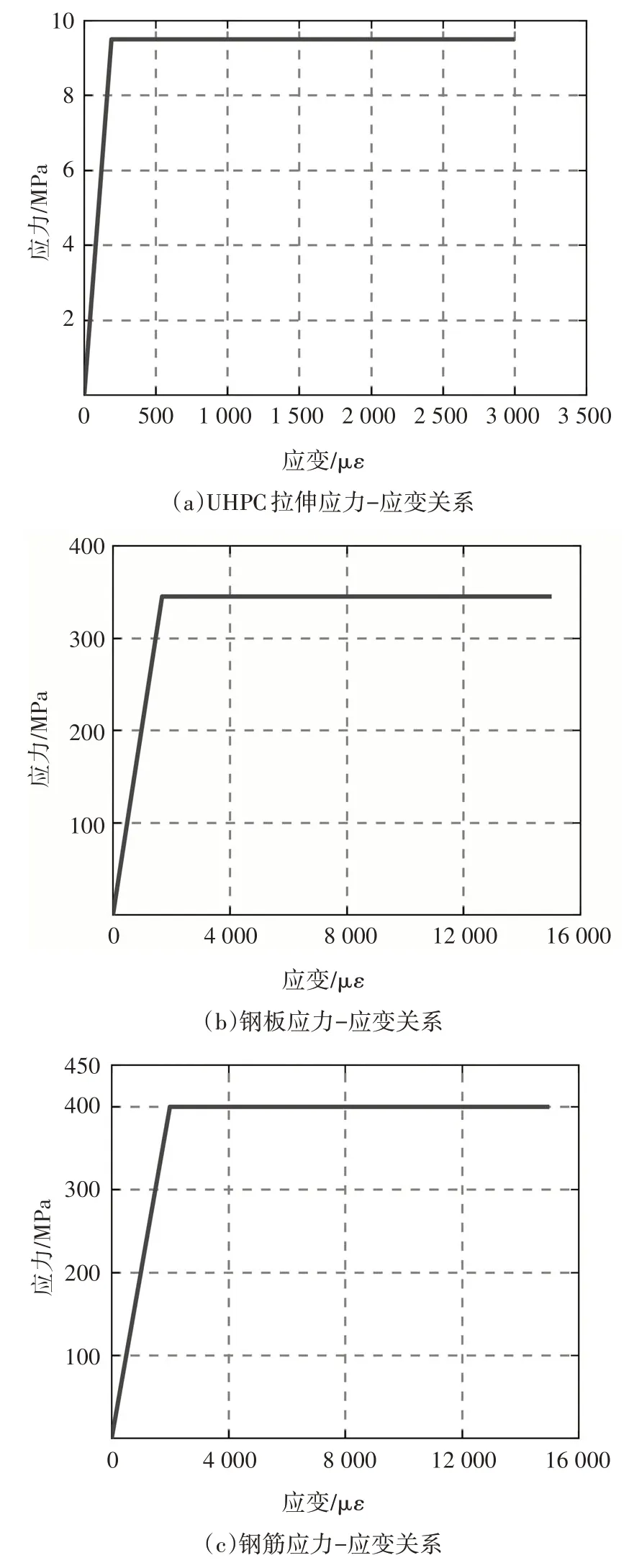
圖24 本構關系模型Fig.24 Constitutive models

基于上述兩種理論的極限抗彎承載力計算模式如圖25所示.

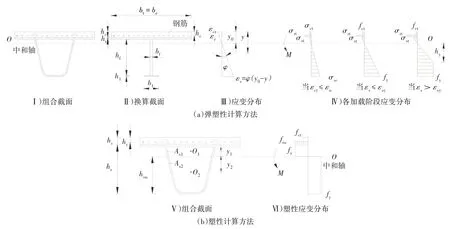
圖25 抗彎承載力計算簡圖Fig.25 Calculation diagram of bending capacity

根據截面平衡條件可列出如下計算公式：

4.7.1 彈塑性計算方法

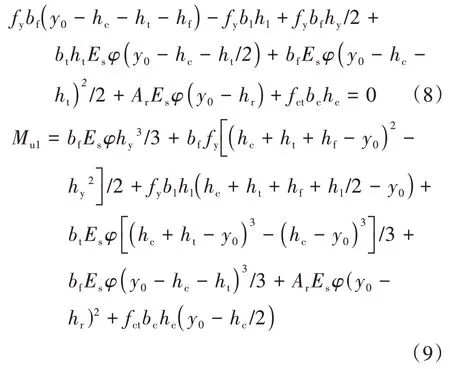
式中：bc為UHPC 板寬度；hc為UHPC 層厚度；ht為鋼面板厚度；hf為換算截面腹板的等效高度；hl為U 肋底部鋼板轉換后的厚度；hr為鋼筋中心距UHPC 板上緣的距離；bl為U 肋底部鋼板轉換后的寬度；bf為換算截面腹板的等效厚度；y0為中性軸至UHPC頂面的距離，中性軸位置隨荷載變化，圖25 中僅作示意；hy為鋼結構受壓屈服區的高度；φ為截面彎矩曲率.hy=fy/(φ?Es)；fct為UHPC 材料軸拉可視初裂應力（裂縫寬度為0.05 mm）；Ar為縱向受力鋼筋的截面面積；Es為鋼材的彈性模量；Ec為UHPC 的彈性模量；fy為鋼板屈服強度；Mu1為試件的彈塑性抗彎承載力.圖25 中，y為截面任意高度位置至UHPC 頂面的距離；εct為UHPC 頂面應變；εu為UHPC 頂面達到軸拉可視初裂應力時的應變；εr為鋼筋應變；εs為鋼板應變；εsy為鋼板屈服應變；σrt為鋼筋應力；σst為鋼面板頂面應力；σsc為U 肋底面應力；σct為UHPC 頂面應力.

4.7.2 塑性計算方法

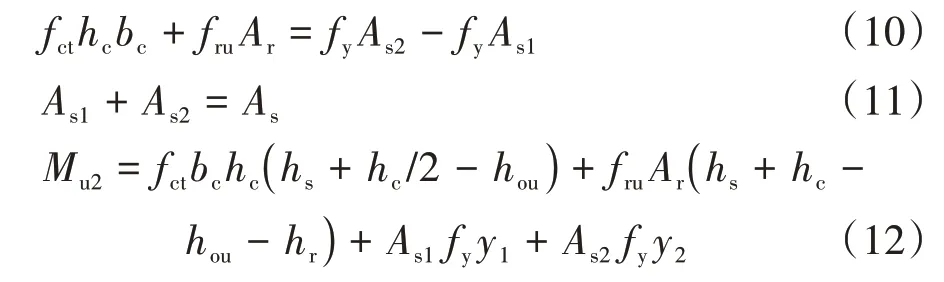
式中：Mu2為試件的塑性抗彎承載力；fru為鋼筋的屈服強度；hou為塑性中和軸距U 肋受壓區底板的距離；hs為鋼梁的高度；As1為組合截面中性軸以上鋼梁截面面積；As2為組合截面中性軸以下鋼梁截面面積；y1為As1形心至塑性中和軸距離；y2為As2形心至塑性中和軸距離；As為鋼梁截面面積.

由于本文已開展了剩余承載力試驗，本節根據實際試驗數據來確定極限狀態.實際試件均以U 肋底板壓屈為最終破壞狀態，U 肋受壓區底部鋼板達到極限強度時，組合梁達到極限承載力，在此狀態下認為平截面假定仍然成立，如圖22 所示，此時鋼板應變接近15 000 με，因此按彈塑性理論計算時，假設εs=15 000 με 時為鋼板極限強度時對應的峰值應變.此外，雖然UHPC 層出現了一定程度的開裂，但根據試驗現象，試件仍表現出優異的剩余承載性能，因而計算中未考慮UHPC 層因疲勞損傷引起的強度變化.

計算結果如表5 所示，可以看出：1）試件經過疲勞加載后極限承載力大于計算值，表明兩種計算方法均偏于安全；2）雖然試件經過疲勞加載，且在試驗中有一定的疲勞損傷，但無論是彈塑性理論或塑性理論均能偏保守地預測試件的剩余承載力，表明疲勞損傷對輕型組合橋面結構的剩余承載力無顯著影響；3）對比基于兩種理論的計算結果可以看出，塑性計算方法吻合度更高，而彈塑性計算方法安全儲備更高.

表5 抗彎承載力計算值與試驗值對應表Tab.5 Comparison of flexural capacities obtained in theoretical analysis and experimental test

5 結論

本文探究了栓釘間距對鋼-薄層UHPC 輕型組合橋面結構疲勞損傷演化特性的影響規律，并關注了栓釘焊趾處鋼面板的拉-剪耦合疲勞狀態.隨后進行了剩余承載力試驗，探明了栓釘間距對疲勞損傷后UHPC 抗裂性能及組合構件抗彎承載力的影響規律，主要結論如下：

1）疲勞試驗中，各加載階段UHPC 的拉應變隨著疲勞加載次數的增加大體呈增大趨勢，而UHPC裂縫擴展較為緩慢；對于U 形肋受壓區底板應變，當栓釘間距為100 mm 和150 mm 時，整個疲勞過程幾乎無變化，而當栓釘間距為300 mm，應變呈微小的增大趨勢；栓釘間距對試件靜力滑移性能影響較大，當栓釘間距為300 mm時，單位荷載下的鋼-UHPC界面滑移明顯高于其他兩個試件，但在疲勞加載過程中，界面滑移的增長并不明顯.

2）試驗中試件S100除在U肋與鋼面板位置焊縫出現斷裂外，其余試件均未發生疲勞破壞.為分析栓釘根部位置鋼面板的拉-剪耦合疲勞受力狀態，以現行《公路鋼混組合橋梁設計與施工規范》為基礎，根據Miner 線性疲勞損傷準則將試驗中的變幅疲勞應力幅換算至200 萬次疲勞循環對應的等效應力幅.對比試驗中的鋼面板拉-剪等效應力幅與現有規范計算公式表明，即使試驗中的耦合疲勞應力幅超過了規范中的疲勞強度包絡線，該疲勞細節仍未發生疲勞破壞.因此，可基于《公路鋼混組合橋梁設計與施工規范》的方法對輕型組合橋面結構中的鋼面板進行拉-剪耦合疲勞驗算，能夠獲得偏于安全的計算結果.

3）剩余承載力試驗表明，栓釘間距越大，鋼板與UHPC 結合面的滑移越大，試件的剩余承載力越低.分別按彈塑性和塑性理論計算試件的剩余承載力，實際承載力仍大于計算值，表明雖然試件經過疲勞加載存在一定的疲勞損傷，但疲勞損傷對輕型組合橋面結構的剩余承載力無顯著影響.對比基于兩種理論的計算結果可以看出，塑性計算方法吻合度更高，而彈塑性計算方法安全儲備更高.