VTI 介質彈性波頻率域多核并行正演模擬
岳曉鵬,付亞運,陳康靖
(許昌學院數理學院,河南 許昌 461000)
在地球內部廣泛存在各向異性,如西非洲海岸、墨西哥灣及中國南海部分區域都存在各向異性地層,橫向各向同性(TI)最為多見的,這種介質具有柱對稱軸,對稱軸在空間垂直的稱為VTI 介質;對稱軸在空間水平的稱為和HTI 介質。正演是偏移和反演的基礎,有限差分正演可以較準確地描述波傳播規律,是波場正演時應用廣泛的方法。頻率域波動方程正演早期由Lysmer 等提出并利用該方法研究了波在各種介質中的特征;Jo 等人提出了減小數值頻散的最優化9點格式[1];Min 等提出了減小了空間采樣點數的25 點差分格式;吳國忱教授用25 點差分格式正演了VTI和TTI 介質[2],還有國內的諸多學者對于VTI 介質的數值模擬進行了研究[3-5]。
頻率域正演優勢在于沒有時間累積誤差[6],每次用獨立的頻率正演,更適用于并行計算[7]。在并行計算研究方面,出現過很多的并行框架,GPU 并行、CPU 并行、集群并行等。很多框架設計結構繁雜,對開發人員要求很高[8,9]。
本研究在詳細分析各種常見并行模式的基礎上,設計了VTI 介質多核并行計算方法。與CPU 串行算法相比,具有較好的加速比。
1 VTI 介質頻率域25 點格式
對于二維VTI 介質質頻率域波方程如下

在式(1)中所有項,利用25 點格式離散時所需的點分布見圖1。
ρω2U 系數見圖1(a),表達式為
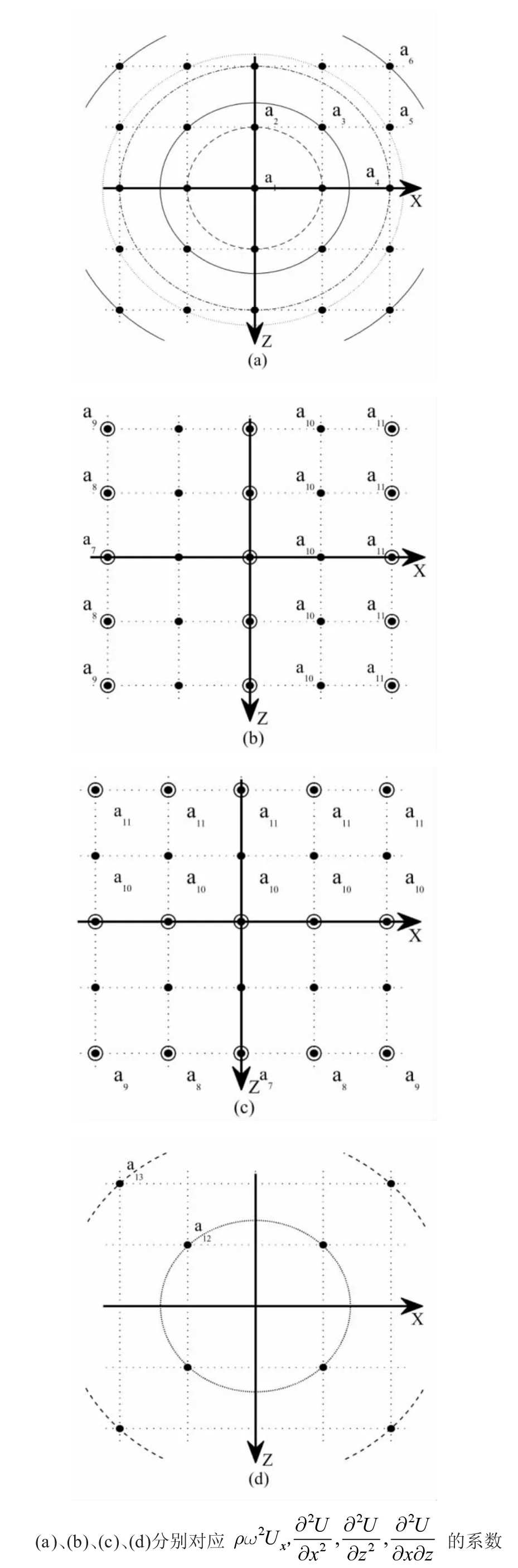
圖1 25 點加權離散示意圖


同理,可以展開其它幾項,將所有算子帶入公式(1)并進行整理后,可以得到矩陣方程

如果網格為N2×Nx,N=Nz×Nx,A 為2N 階矩陣,Y是未知2N×1 矩陣,F 是2N×1 矩陣。
2 數值算例
地質模型為:縱波為4 000 m/s;橫波2 000 m/s;介 質 2 500 kg/m3;NX=160,NZ=160; 空 間 步 長Δx=Δz=5 m,ε=0.5,δ=0.1。邊界是PML 邊界。記錄時間0.3 s,采樣間隔0.001 s,震源是Richer 子波,主頻25 Hz,檢波器在地表按網格排列,震源坐標為(80,80),檢波點坐標(100,100),圖2 和圖3 為數值模擬的波場快照和地震記錄。

圖2 VTI 介質的波場快照(125 ms 時刻)
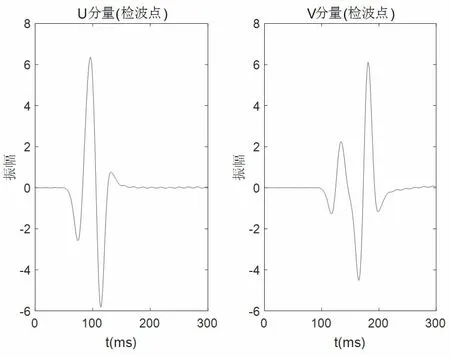
圖3 VTI 介質的地震記錄
3 多核并行正演對比分析
這里采用的多核并行方式是使用Matlab 的多核并行方法。正演模擬時使用的平臺為雙路Xeon E5-2650 v4,32 GB 內存的服務器,共有24 個計算核心。程序運行的主要耗時在矩陣方程(6)的求解上,例如當網格數為160*160 時,矩陣A就是一個80 000 階(200*200*2)的大型稀疏矩陣,求解這樣系數的矩陣方程相當耗費時間。對于VTI 介質頻率域方程,可以采用并行的方式在每個頻點獨立求解。
假設計算網格數分別為100*100、130*130、160*160,190*190、220*220,四周加上PML 邊界后,實際計算網格數為140*140、170*170、200*200,230*230、260*260,對比順序執行和并行求解方程(6)平均耗時及程序運行時間,見表1。
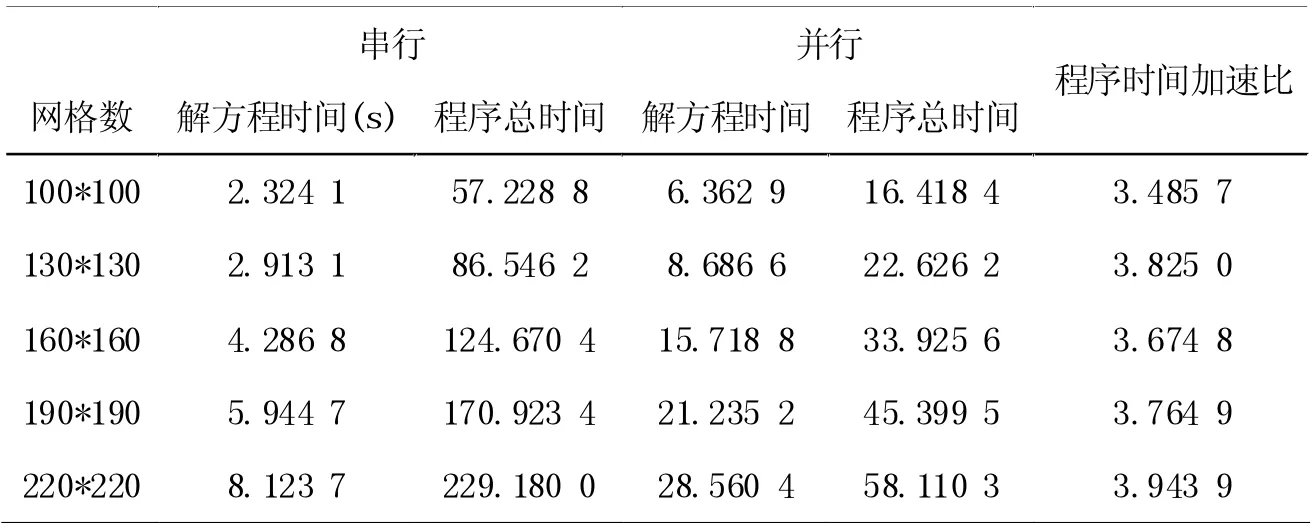
表1 兩種方法耗時對比
為了更直觀的說明問題,將以上數據作圖表示,見圖4。

圖4 兩種方法耗時對比
4 結論
目前,CPU 正在朝著多核心方向快速發展,最新的i9-13900k 已經是24 核32 線程,然而,現有的波動方程正演及偏移成像代碼大多是采用MPI 技術實現并行,這種進程級粒度的計算方式在集群之類的分布式系統上效果很好,在單個計算節點又要受到內存等限制,只能利用少數的計算核心,不能發揮多核處理器的最大效能。本研究將占據波動方程頻率正演模擬主要計算時間的大型矩陣方程求解過程分配給多個計算核心,利用多核心并行計算方法,多個頻點的求解過程可以同步計算完畢,即在進程中實現多核心并行,有效提高了多核處理器的利用效率和代碼執行速度。

