改進黑猩猩優化算法的測試數據生成研究

高大喚，梁宏濤，杜軍威，于 旭，胡 強

青島科技大學 信息科學技術學院，山東 青島 266100

隨著軟件規模、需求及復雜度的不斷提升，軟件缺陷率不斷增長[1-2]，而發現軟件缺陷的唯一途徑就是對軟件進行測試。軟件測試作為軟件工程生命周期中的關鍵階段之一，其中測試數據縱貫軟件測試的全部流程。軟件測試的主要目標是生成有效的測試數據，而如何在有限的時間內生成有效的測試數據是軟件測試領域的研究難點之一[3]，在有限的時間內選擇一組代碼覆蓋率較高的輸入數據是自動化測試數據生成技術的主要目標[4]。在軟件測試技術的探索中，出現了眾多測試數據生成方法，基于啟發式的生成算法成為當下學者的研究主流，并被廣泛應用到測試數據[5-9]。

啟發式優化算法在測試數據生成中的應用可追溯到1976年，當時美國研究人員Miller和Spooner[10]試圖在浮點測試數據生成中使用搜索算法，但是他們沒有繼續相關的工作；Khan等[11]將遺傳算法和變異分析方法進行融合用于測試數據自動生成，但只有運行變體，才能得到這個變體的分數，這就導致運行時間有所增加；何海鮮等[12]提出將布谷鳥改進算法用于測試數據自動生成，證明效果優于其他算法，但是在降低冗余數據的生成效果方面并不明顯；Sahoo和Ray等[13]在測試數據生成中使用改進組合適應度函數的粒子群算法可有效提高路徑覆蓋數量，但未考慮到覆蓋多個關鍵路徑的測試數據生成效率；Mahdieh等[14]提出將故障傾向性估計納入測試數據的優先級排序中可提高測試數據的生成及優先級排序效率，不足的是未考慮開發過程歷史中的測試用例執行結果；何慶等[15]提出了在黑猩猩優化算法中融合多策略，提高了算法的收斂速度，并在機械設計中得到很好的運用和效果，算法雖整體性能提高得不少，但其收斂速度相對過快。

雖上述文獻對各種啟發式優化算法進行改進，在一定程度上能改善算法的尋優精度和收斂效果[16-18]，進而提高測試數據的生成效率，但目前測試數據生成大多集中在啟發式搜索算法的某些單一算法上，如遺傳算法、蟻群算法等，這種算法有一些先天的局限，如過早收斂、搜索精度不足、容易陷入局部最優解等[19-20]。另外，在測試數據生成方面對于新型的算法研究相對較少。黑猩猩優化算法[21]（chimp optimization algorithm，ChOA）是2020年由Khishe等提出的一種新型算法。它不僅具有流程簡單、參數少、能與各種優化問題結合的優點，還具有兩大主要特點：一是將種群劃分為一個個獨立的個體，可以有效提高算法的勘探能力；二是引入混沌因子，有助于改善開發過程的收斂速度和精度[22]。不足是ChOA算法也存在易陷入局部最優和收斂過早等問題。因此，本文提出一種正余弦擾動策略黑猩猩優化算法，先使用拉丁超立方策略初始化種群，增加群體多樣化；其次引入非線性衰減收斂因子來平衡全局和局部開發能力；然后在位置更新時添加正余弦擾動因子，防止算法發生停滯現象；另外考慮到該算法目前尚未在測試數據生成領域中得到應用，因此考慮將其應用到測試數據的自動生成中；最后通過實驗對比驗證算法有效性及在測試數據生成中的生成效率和可行性[23]。

1 黑猩猩優化算法

ChOA是由Khishe于2020年提出的一種較為新穎的啟發式搜索算法，它的原理是仿照黑猩猩的社會行為進行狩獵進而達到尋優的目的，分為四類黑猩猩[24]，即，攻擊黑猩猩（attacker）、驅逐黑猩猩（driver）、阻礙黑猩猩（barrier）和追趕黑猩猩（chaser），四類黑猩猩中攻擊黑猩猩是領導者，其他三類配合領導者進行打獵。下面是黑猩猩在驅逐和追趕獵物過程的數學模型：

其中，t為當前迭代次數，D是黑猩猩與獵物間的距離，XP為獵物的位置，XC為黑猩猩的位置，A、C、m均為系數矢量，且A是決定黑猩猩與獵物距離的系數矢量，C是控制黑猩猩驅逐和追趕獵物的系數矢量，m表示社會激勵對黑猩猩個體位置的影響，A、C、m的表達式為：

其中，R1、R2屬于[0，1]區間內的隨機值，f為線性遞減因子。

四種黑猩猩的位置更新公式如下：

其中，X為當前黑猩猩的位置，Xa、Xb、Xc和Xd分別表示攻擊黑猩猩、阻礙黑猩猩、驅逐黑猩猩及追趕黑猩猩的位置，X(t+1)表示更新后t+1代黑猩猩的位置，C1、C2、C3和C4均為隨機分別在[0，1]區間的數。

在狩獵過程黑猩猩位置更新的數學模型如下：

其中，μ是隨機分布在[0，1]區間內的數，Chaotic-value為混沌因子。

2 改進黑猩猩優化算法

目前，在基本的ChOA中，使用隨機分布的方式初始化種群，這種方式導致種群的多樣性降低；其次，算法使用線性收斂因子來平衡全局和局部開發能力，會導致算法尋優速度遲緩；最后，原始算法存在易陷入局部極值現象。因此，針對基礎算法存在的局限，提出多種改進策略，具體介紹如下。

2.1 拉丁超立方策略初始化種群

很多原始的啟發式優化算法均采用隨機方式初始化種群，隨機分布具有隨機性、不確定性，這種方式會導致種群分布不均及算法搜索能力下降，但是群體優化算法又依賴于群體的初始化位置。而混沌狀態是自然界普遍存在的一種非線性現象，具有遍歷性、不重復性和對初始值敏感性的特點，很多學者根據這些特點將其應用于到算法優化問題。目前大多數文獻常用的混沌映射是Logistic映射，但是Logistic映射存在中間分布均勻、兩端分布密集的問題。針對上述存在的問題，本文提出采用拉丁超立方初始化種群，由于它具有均勻分層的特征，可以均勻遍布整個空間，覆蓋率更高，能以較小的采樣規模獲得較高的采樣精度，因此，LHS映射比隨機方式和Logistic映射分布較為均勻，用來初始化種群的效果更佳，三種方法的對比效果如圖1所示。

圖1 LHS、Logistic及隨機方式的頻率分布直方圖Fig.1 Frequency distribution histogram of LHS，Logistic and Random

設全局搜索范圍[UB,LB]，初始種群規模為N，每維xi變量的定義域區間劃分為N個相等的小區間，數學模型如下：

設搜索空間是二維空間，拉丁超立方初始化種群如圖2（a）和（b）所示。

圖2 拉丁超立方初始化種群分布映射和直方圖Fig.2 Latin hypercube initialization population distribution map and histogram

由圖2可知，拉丁超立方初始化種群可使種群分布得更加均勻，覆蓋率更加廣泛，因此，采用拉丁超立方進行初始化種群可以提高種群的多樣化和種群的質量。

2.2 非線性衰減收斂因子

動態變化的衰減收斂因子種類繁多，如：線性衰減收斂因子、高斯衰減收斂因子、對數衰減收斂因子、指數衰減收斂因子等，在標準的ChOA中，一般采用線性遞減因子來控制算法的全局和局部開采能力，但是這種方式并不能較好地權衡算法的全局和局部勘察能力，導致算法搜索速度遲緩，圖3是5種收斂因子對比曲線圖。

圖3 收斂因子曲線圖Fig.3 Convergence factor graph

圖3中可以看出，在5種遞減策略中，雖然不同策略在不同程度上都可以平衡算法的探索和開發能力，但是如果在尋優初期收斂因子衰減過快，會使算法全局探索能力變弱，存在易陷入局部極值的問題，所以非線性立方衰減策略更具優勢，因此，本文提出一種非線性立方衰減收斂因子。在算法迭代初期先擴大算法的搜索空間進行大范圍的全局開采，提高算法的尋優效果，在此過程中收斂因子逐漸下降，算法開始收縮搜索范圍進行小范圍的局部開發，局部勘察有助于算法在短時間內找到最優值。非線性立方衰減收斂因子的數學模型為：

其中，t當前迭代數，Tm為最大迭代數，f"為非線性衰減收斂因子。

標準ChOA算法中的線性收斂因子呈線性衰減，而本文提出的非線性立方衰減因子呈非線性衰減，這種方法不僅增大了算法的搜索范圍，提高了算法的全局開拓能力，也有利于算法的局部開采，提高算法的尋優精度，避免算法陷入局部極值，縮短算法的尋求最優值的時間成本。

2.3 正余弦擾動因子

在標準的ChOA算法中，黑猩猩位置更新主要靠每次迭代進行更新，通過計算適應度值，選擇其中最優的作為攻擊者黑猩猩，攻擊黑猩猩是四類黑猩猩的領導者，其位置更新的好壞直接決定了整體算法尋優的效率和準確度，但是這種對攻擊者黑猩猩的強依賴性不利于算法的尋優。當陷入局部范圍搜索時，其周圍將聚集大量其他黑猩猩，進而會導致算法陷入局部最優，無法探索搜索空間中的新區域。為了避免這種現象，本文提出將正余弦波信號進行改進后的正余弦波因子融入到黑猩猩位置更新過程，引入該因子可使算法跳出局部范圍，提高算法的尋優能力，使其避免墜入局部最優，其迭代100次的圖形如圖4所示。

圖4 正余弦擾動因子分布Fig.4 Sine and cosine perturbation factor distribution

利用正余弦擾動因子動態變化的不確定性對四類黑猩猩在位置更新時進行不同程度的擾動，使得四類黑猩猩能向更廣泛的區域進行搜索，擴大了算法的搜索規模，降低了其他黑猩猩盲目跟隨攻擊者黑猩猩的概率，提高了算法跳出局部極值的能力。

正余弦擾動因子的數學模型公式如下：

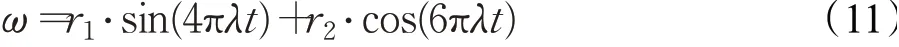
其中，r1、r2屬于[0，1]區間內的隨機值，λ是控制參數。

在標準ChOA中引入正余弦擾動因子后的四類黑猩猩的位置更新公式為：

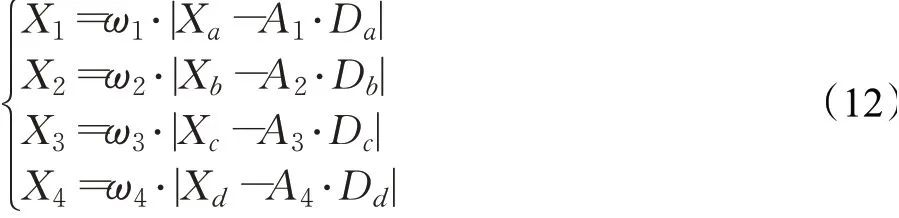
2.4 算法實現流程

綜合上述改進策略，本文提出的正余弦擾動策略黑猩猩優化算法（SC-ChOA），它是在標準的ChOA基礎上進行的改進，引入三個策略，其一使用拉丁超立方初始化種群，其二將ChOA的線性收斂因子改進為非線性衰減收斂因子，其三對標準ChOA主要依賴攻擊黑猩猩的特點進行改進，使用正余弦擾動因子對四類黑猩猩位置進行擾動。SC-ChOA算法的輸入為拉丁超立方初始化種群及相關參數，輸出為最優黑猩猩個體的位置，具體實現步驟及偽代碼如下：

步驟1初始化種群規模，最大迭代次數Tm、搜索范圍UB、LB，并設置相應參數。

步驟2采用LHS初始化種群Xi，i=1,2,…,N。

步驟3計算每個個體的適應度值，找出最優的前四個值記為四種黑猩猩個體，分別記為Xa、Xb、Xc和Xd。

步驟4根據公式更新系數向量A、C及非線性衰減收斂因子的值f"。

步驟5通過正余弦擾動因子進一步更新四類黑猩猩的位置及其他黑猩猩的位置。

步驟6判斷是否達到最大迭代次數，若無，則跳轉到步驟3，否則結束算法，并輸出最優黑猩猩的位置Xa。

SC-ChOA算法流程如圖5所示。

圖5 SC-ChOA算法流程圖Fig.5 SC-ChOA algorithm flowchart

2.5 時間復雜度分析

算法的時間復雜度是關于輸入規模n的函數，可直接反映算法的收斂速度，用來檢驗算法運行效率的關鍵指標，在標準ChOA算法中，假設種群規模N，搜索空間維度n，參數初始化時間為t1，隨機初始化種群的時間為t2，則標準ChOA初始化階段的時間復雜度為：

設計算種群個體適應度值所需時間為f(n)，選擇前四個最優值個體位置的時間為t3，更新線性衰減收斂因子的時間為t4，根據前四個最優個體更新種群其他黑猩猩個體位置所需時間為t5，則標準ChOA迭代尋優階段的時間復雜度為：

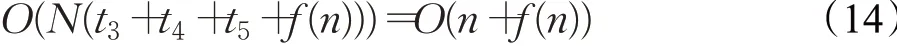
因此，標準的ChOA算法迭代尋優過程總的時間復雜度為：

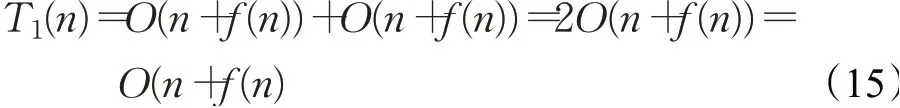
在SC-ChOA算法中，初始化相關參數所需時間與標準ChOA相同，采用拉丁超立方策略初始化種群所需時間為t6，在算法迭代階段非線性衰減收斂因子遞減時間為t7，執行正余弦擾動因子的時間為t8，更新四類黑猩猩位置所需時間為t9，則SC-ChOA算法的時間復雜度為：

根據相關文獻研究表明，遺傳算法（genetic algorithm，GA）的時間復雜度為：

綜上所述，SC-ChOA算法和標準ChOA算法的時間復雜度屬于同一數量級別，對算法改進并沒有增加算法的時間復雜度，且均小于GA算法的時間復雜度，即：

3 實驗仿真與結果分析

3.1 實驗設計與測試函數

實驗設備：Windows 10操作系統，計算機處理器3.30 GHz，內存16 GB，算法使用MATLAB R2016a編寫。為了評價SC-ChOA算法的實際效果，與標準的ChOA[25]及常用的GA[26]進行實驗對比，選擇10個不同特征的測試函數，其中f1～f5為單峰值函數；f6～f8為多峰值函數；f9～f10為固定維度多峰函數，如表1所示。

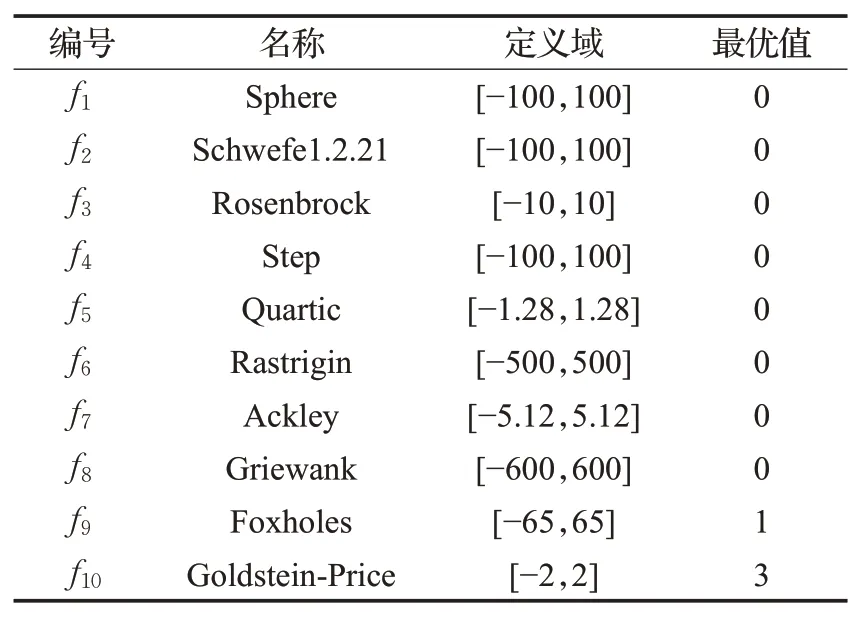
表1 測試函數Table 1 Test function

3.2 算法尋優性能分析

為了證明改進算法SC-ChOA的有效性及其動態收斂性，將本文加入的拉丁超立方初始化、非線性衰減收斂因子及正余弦擾動因子三個策略的SC-ChOA算法與標準ChOA算法及GA算法在10個不同特性的測試函數上進行實驗對比。

為確保實驗公平性，取空間維度d=30，最大迭代次數Tm=100，群體規模N=30，每個函數運行30次，取最優值、平均值、標準差及算法的運行時間四個性能指標來評價每個算法的尋優效果，最優值和平均值可以用來反映算法的尋優效果和收斂速度，標準差可以反映算法的穩定性和魯棒性，運行時間對應算法的收斂速度，運行時間越少，說明算法收斂速度越快，反之亦然，具體對比結果如表2所示。

通過表2的最優值和平均值可直接反映出算法的尋優效果和收斂速度的能力。首先，從最優值的結果可以看出，SC-ChOA在求解單峰函數f2、f4及多峰函數f6時均取得了最優值0，在求解兩個固定維度多峰函數f9和f10時，也取得了最優值1和3。在求解多峰值函數f7的最優值時，因為f7是山谷形狀的，其全局最優值位于山谷最低端，很難取到最優值，但是SC-ChOA和ChOA的平均尋優精度可達到10-80以上，而GA的平均尋優精度只能達到10-70以上，另外，SC-ChOA相比于ChOA和GA在達到尋優精度的基礎上，其運行時間也比標準ChOA和GA的運行時間少，這說明SC-ChOA在求解最優值時不論單峰函數、多峰函數還是固定維度的多峰函數，SC-ChOA算法都具有良好的穩定性和魯棒性。其次，從平均值的結果可以看出，標準ChOA求解函數最優值的尋優能力有限，而SC-ChOA在f2、f4和f6均獲得了最優解，這是因為在標準ChOA中引入了正余弦擾動因子對函數局部最優解進行了擾動，使其向全局最優解靠攏，提高了算法的尋優精度和收斂速度。在求解f5和f7時，SC-ChOA和ChOA的尋優精度達到級別相近，均可直接收斂到最優解附近，但是SC-ChOA相比于ChOA的運行時間少很多，提高了收斂速度，這是因為在標準ChOA中引入了非線性立方衰減收斂因子，有效平衡了算法的全局和局部搜索能力，加快算法收斂速度，縮短算法的尋求最優值的時間成本。對于形狀類似于拋物面存在大量的局部極值的函數f1、f2、f3和f8，僅有改進的SC-ChOA取得了最優值，而標準ChOA和GA均未取得最優解，這說明在標準ChOA中引入三個策略得到的SC-ChOA算法更有助于求解具有大量局部極值的函數。綜上所述，無論在尋優精度還是穩定性上，融入三種策略的SC-ChOA均表現出一定的優勢。

表2 10個測試函數實驗結果Table 2 Experimental results of 10 test functions

3.3 算法收斂性分析

為了更加直觀地反映三種算法在求解不同特征測試函數f1～f10的尋優精度和動態收斂性，圖6給出了三種算法在10個測試函數的收斂曲線圖。

由圖6可以看出，對于10個測試函數，SC-ChOA在算法迭代初期的收斂曲線下降速度較快，在迭代末期的開拓性能也優于其他兩個算法，且在整個尋優迭代過程，SC-ChOA的收斂曲線均在ChOA和GA下面，這表明引入的拉丁超立方初始化種群和非線性衰減收斂因子策略不僅能保證算法的全局開拓能力和種群的多樣性，也有效提高了算法的收斂速度。圖6（a）～（e）是單峰函數的收斂曲線圖，從圖中可以看出，ChOA算法的收斂曲線在迭代初期T=30附近，均出現陷入算法停滯的現象，而改進算法SC-ChOA在迭代初期可以快速下降，且在整個迭代過程沒有出現明顯的陷入算法停滯的狀態，這表明融入的正余弦擾動因子策略能帶領群體找到全局最優值，有助于群體跳出局部極值，進而有效地改進了標準ChOA算法存在的易陷入局部極值的問題，并且加入了非線性立方衰減收斂因子可有效平衡算法的全局和局部勘察能力；圖6（f）～（h）是多峰函數的收斂曲線圖，從圖中可以發現SC-ChOA的收斂曲線在整個迭代過程可快速下降，并取到最優解，雖然在算法迭代初期ChOA的收斂曲線也可以快速下降，但其存在算法停滯現象，如f8在迭代次數T=40次后，算法沒能跳出局部極值完全進入了停滯狀態，導致算法最終未取到最優解。而GA均為未取到最優值，且SC-ChOA和ChOA的尋優精度均比GA提高了至少50個數量級，這說明新型黑猩猩優化算法的尋優效果明顯優于傳統的遺傳算法。對于函數f6、f7，雖然SC-ChOA和ChOA都能達到尋優精度，但是SC-ChOA達到尋優精度時所用的迭代次數明顯小于ChOA，如對于f6，SC-ChOA找到最優值時所用的迭代次數大約為50次，而ChOA找到最優值時所用的迭代次數大約為70次；對于f7，SC-ChOA找到最優值時所用的迭代次數大約為30次，而ChOA找到最優值時所用的迭代次數大約為50次，這進一步說明了引入正余弦擾動因子和非線性衰減收斂因子策略的SC-ChOA可以提高算法的收斂速度，減少算法找到最優解時所消耗的迭代次數。圖6（i）、（j）是固定維度的多峰函數的收斂曲線圖，從圖中可以看出，三種算法均可達到尋優精度，且SC-ChOA和ChOA的收斂曲線下降速度高于GA，另外，對于f9，SC-ChOA和ChOA找到最優值時所用的迭代次數大約分別為35次、80次；對于f10，SC-ChOA和ChOA找到最優值時所用的迭代次數大約分別為60次、90次，這明顯可以看出融入三種策略的SC-ChOA相比于標準ChOA在算法整個尋優過程中的收斂速度有很大程度的提高，且SC-ChOA和ChOA均優于GA。

圖6 三種算法收斂對比圖Fig.6 Convergence comparison chart of three algorithms

綜上所述，表2的實驗結果與圖6的收斂曲線驗證了本文所提改進算法的有效性。SC-ChOA均達到了尋優精度，且收斂速度也是相對較快的，雖然ChOA在某些測試函數上未取到最優值，但是其收斂速度優于GA算法。因此，對于單峰函數、多峰函數及固定維度的多峰函數，無論在尋優精度上，還是收斂速度上，SCChOA相比于ChOA和GA均具有較好的尋優性能和收斂速度。

4 SC-ChOA測試數據生成應用與分析

測試數據生成問題是軟件測試領域普遍關注的重要問題，測試數據的生成效率直接決定了軟件測試的整體效率。在軟件測試技術的探索中，出現了眾多測試數據生成方法，其中，基于啟發式優化算法成為當下學者的研究主流，其思想是將測試數據生成問題通過適應度函數轉化為一個函數最優化問題，然后利用啟發式優化算法進行求解。本文為驗證改進算法SC-ChOA在解決實際問題中的有效性，將其應用于測試數據生成中，下面進行詳細的介紹。

4.1 測試數據生成模型框架

測試數據生成模型主要包括3個模塊：

（1）靜態分析模塊

通過對測試程序的分析，得到程序控制流程圖，從中選擇測試程序的目標路徑，并得到算法的部分參數。同時，根據流程圖得到測試主程序的插樁程序。

（2）測試驅動模塊

該模塊主要負責建立適應度函數，在測試運行的過程中，輸入為算法返回的測試數據集，使用這些測試數據集驅動被測程序。并且通過適應度函數評價測試用例，返回適應度值給算法部分。

（3）算法生成測試數據模塊

該模塊是測試數據自動生成的重要模塊。算法完成初始化任務后，將初始數據輸入到測試驅動模塊，對測試驅動模塊傳來的適應度值進行檢查，判斷當前運行結果是否是最優解或迭代次數達到最大，若符合條件，算法終止，輸出最優的測試數據，否則繼續迭代，直到找到最優解。改進啟發式搜索算法的測試生成模型框架如圖7所示。

圖7 基于SC-ChOA算法的測試數據生成模型框架Fig.7 Test data generation model framework based on SC-ChOA algorithm

4.2 程序插樁技術與適應度函數構造

4.2.1 程序插樁技術

程序插樁技術是由Gallagher提出的，思想是在每個語句分支中插入適當函數獲取執行時的信息，來評價測試數據。被測程序的測試技術是由Huang最先發明的，在程序結構中添加代碼來收集程序執行信息，并用以記錄在驅動程序工作過程中測試結果的內在活動和關鍵特性[27]。

測試數據自動生成系統的主要實現方式是基于測試程序中的樁插入，其基本思路為：

（1）首先對數據進行隨機初始化；

（2）判斷單個驅動程序執行路徑與目標路徑的偏差；

（3）最后采用逐步迭代的方法生成測試數據。

為了更好地解釋程序插樁法，以三角形類型判斷為例進行插樁，三角形決策流程圖如圖8所示。

圖8 三角形類型判定程序流程圖Fig.8 Flowchart of triangle type judgment program

以下是插樁后的三角形類型判別MATLAB源代碼：

4.2.2 構造適應度函數

算法是否需要進行迭代的依據是個體的適應度值，適應度函數的構造是測試操作模塊的關鍵技術，也是SC-ChOA算法應用于測試數據自動生成的重要環節，測試數據的生成轉化為使用SC-ChOA算法尋找目標函數的最優解的過程，因此適應度函數的構造將影響算法在測試數據自動生成中的效率。適應度函數使用分支謂詞的分支距離計算，如表3所示。

表3 分支謂詞的距離構造函數Table 3 Distance constructors for branch predicates

評價測試數據的好壞的一個重要標準是程序執行過程的覆蓋率，計算覆蓋率首先需要對被測程序的分支進行插樁，再對被測程序的目標路徑進行插樁。覆蓋率公式為：

其中，Xi表示第i分支的測試數據，x表示該分支的值，f(i)表示第分支的覆蓋率。若f(i)≤0表示覆蓋該分支，則令f(i)=0；若f(i)＞0，則該值就是測試數據和分支的距離，值越大意味著測試數據離分支越遠。總的適應度函數公式如下：

其中，F的取值范圍在（0，1]之間，值越大則表示測試數據越好。當F=1時，表示該測試數據可完全覆蓋該目標路徑。

4.3 應用與分析

實驗選取7個常用的程序作為基準程序，這些程序具有代表性，不僅包含選擇結構、循環結構及復雜的嵌套結構，還含有算術運算符、關系運算符和邏輯運算符及整型、浮點型、字符型、字符串等數據類型，常被用于測試數據生成領域。程序的具體描述，其程序ID、變量數、分支數、搜索范圍和程序描述如表4所示。

表4 測試基準程序Table 4 Test benchmark

為保證實驗的公正性，3種算法在某些參數設置上保持一致，如群體大小、最大迭代次數等，其他參數參考其他文獻設置，并使用迭代次數、覆蓋率、生成測試數據數及運行時間為評價標準。

以三角形類型判定程序為例，通過三種算法進行實驗比較，取平均值為評價標準。實驗結果的相關數據如表5所示。

表5 三角形類型判別程序實驗結果Table 5 Experimental results of triangle discriminator

由表5可知，改進算法SC-ChOA和標準ChOA比GA算法具有更高的效率，且覆蓋率均達到了100%，而GA覆蓋率只達到了90%，這是因為GA算法未生成覆蓋目標路徑等邊三角形的測試數據。雖然標準ChOA和改進算法SC-ChOA的覆蓋率都達到了100%，但是SC-ChOA在生成覆蓋目標路徑的測試數據時，生成測試數據總數僅有517個、所用的迭代次數只有14次，而ChOA相對于SC-ChOA產生了較多的冗余測試數據，且所用的迭代次數遠大于SC-ChOA。因此，SC-ChOA相比于ChOA和GA在生成滿足條件的測試數據效率方面及降低所用迭代次數上均具有一定的優勢。為了更直觀地看出三種算法在生成測試數據上的對比效果，圖9是程序1使用三種算法生成覆蓋目標路徑的測試數據總數和迭代次數的直方圖。

圖9 程序1生成的測試數據總數和迭代次數Fig.9 Total number of test data and number of iterations generated by program 1

使用和三角形類別判定同樣的方法及參數設置對表2中其他測試程序進行對比實驗，為了更直觀地看出SC-ChOA算法與其他兩種算法在生成測試數據方面的效率，圖10（a）和（b）是生成滿足目標路徑的測試數據所生成的測試數據總量及迭代總數。

圖10 七個基準程序測試數量和迭代次數對比Fig.10 Comparison of number of tests and number of iterations for seven benchmarks

由圖10可以看出，本文提出的SC-ChOA算法生成滿足目標路徑的測試數據總數和此過程所用的迭代次數的折線圖均在ChOA和GA下面，這說明了改進的SC-ChOA算法不僅提高了測試數據生成的效率，減少了冗余數據的生成，還降低了生成滿足條件的測試數據所使用的迭代次數，這是因為在標準ChOA引入了正余弦擾動因子和非線性衰減收斂因子，使算法更好地平衡全局和局部搜索能力，避免算法陷入局部最優，減少了迭代次數，進而降低了冗余數據的生成。因此，SCChOA算法相比于其他兩種算法在測試數據生成效率方面更具有優勢。

圖11是對七個基準程序進行10次實驗所使用的運行時間，可明顯看出，SC-ChOA算法很大程度上降低了在生成滿足條件的測試數據的運行時間，這歸因于SC-ChOA算法的尋優精度和收斂速度優于其他兩種算法。

圖11 七個基準程序三種算法運行時間Fig.11 7 benchmark program run-time of three algorithms

綜上所述，本文提出的改進算法SC-ChOA可有效平衡整體和局部搜尋，不僅在測試數據生成的覆蓋率上有所提高，還降低了生成測試數據的迭代次數和時間，進而改善了測試數據的生成速率和效果。

5 結束語

為提高測試數據的生成效率，本文對標準ChOA進行改進提出引入多攻略的正余弦擾動黑猩猩優化算法并將其用于測試數據生成方面。首先，引入拉丁超立方初始化種群，增加種群的多樣化；其次，對標準ChOA算法進行改進，并提出非線性衰減收斂因子，用于權衡算法的全局勘察和局部開采能力，縮短算法的收斂時間，進而加快收斂速度；另外，在黑猩猩每次迭代過程中融入正余弦擾動因子，阻止算法陷入局部范圍搜索，而導致算法出現停滯現象；最后，使用測試函數與標準ChOA算法及GA算法進行實驗對比，驗證算法的有效性，并將其應用于測試數據生成領域。通過基準程序對三種不同算法進行實驗對比，結果表明，本文提出的算法SC-ChOA更加有效，可以應用于軟件測試的全過程。在未來的工作中，將進一步思考如何將該算法與其他智能優化算法進行合理的融合，使其更好地應用于測試數據的生成及并行測試中。