融合后驗概率和密度的不平衡數據欠采樣方法

任艷平，鄭 重，江一飛，嚴遠亭，張燕平

安徽大學 計算機科學與技術學院，合肥 230601

近年來，隨著機器學習和數據挖掘等技術快速發展，越來越多的機器學習算法從學術界走向工業界。然而這一過程也面臨許多實際問題的挑戰。數據不平衡問題就是一個典型的例子。對一個二分類問題，樣本數量相對較少稱為少數類，樣本數量較多的稱為多數類。數據的不平衡分布對傳統機器學習方法提出了挑戰，這些算法在構建和訓練模型時都有一個基本假設：類間樣本呈均勻分布。將這些算法直接用于不平衡數據時，最終得到的結果往往不是很理想。這是因為以最小化總體誤差為學習目標的傳統分類算法會忽視少數類而過多地關注多數類。但在很多實際應用場景中少數類更值得關注。如醫學診斷[1]、欺詐檢測[2]、破產預測[3]、文本識別[4]、漏油檢測[5]等。

針對不平衡數據的學習問題，學者們從不同角度提出了大量解決方法，這些方法大致可以分為三類：數據層面的方法[6-8]、算法層面的方法[9-10]和集成方法[11]。數據層面的方法通過對不平衡數據重采樣，使不平衡的樣本分布變得相對平衡，從而提高分類器對少數類的識別率。重采樣包括過采樣、欠采樣和混合采樣。算法層面方法通過修改現有算法或提出新算法來解決類不平衡問題。如代價敏感方法，對不同的類別分配不同的誤分類代價，通常賦予少數類樣本更高的誤分類代價，從而增強分類器對少數類樣本的識別能力。集成方法通常結合前面兩類方法構建多個學習器，并采用集成策略將這些學習器組合成一個多分類系統，以此來提升模型的分類性能[12-13]。數據層面的方法是目前解決類不平衡問題的主流方法，它的主要優勢在于其實現簡單且能夠直接應用于傳統機器學習算法。

過采樣和欠采樣是目前使用最多的兩種數據層面的方法。過采樣方法主要通過生成合成新樣本來平衡數據分布。其典型代表有SMOTE[14]、Borderline-SMOTE[15]、ADASYN[16]等。但是如何合理地生成新樣本避免引入額外異常樣本和可能的過擬合問題仍然是過采樣的一大難點[17]。欠采樣方法則是通過選取多數類樣本的子集來緩解類別不平衡現象。相較于過采樣而言，欠采樣方法訓練時間更少，訓練過程中采用的數據都是來自原數據集中的樣本，使得模型更加真實可靠[18]。當前關于欠采樣的研究大多認為不適當的樣本選擇策略所導致的關鍵樣本的信息丟失是影響欠采樣方法性能的主要原因，為此，研究者從不同角度提出了一系列的針對性的方法[19-22]。

與此同時，近年來有研究[23-25]表明，相較于類別不平衡，數據復雜因子如類重疊、子概念、噪聲等對不平衡學習的性能具有更為直接和重要的影響。已有一些研究表明，高效地處理類別重疊能夠有效提升過采樣方法的性能[26-27]。但是，對欠采樣方法中處理類別重疊的相關研究并不多見。欠采樣處理重疊問題主要是為了避免選擇高重疊的樣本。過采樣方法處理重疊問題主要是避免生成的樣本進一步造成重疊，加重采樣之后的重疊程度。這兩種方法處理類別重疊的目的都是為了使平衡后的數據集中的樣本重疊度低，它們的區別主要在于實現途徑不同。為此，本文針對欠采樣過程中的類重疊問題，提出了一種基于后驗概率和分布密度的欠采樣（BPDDUS）方法。該方法的主要思路是先通過樣本的近鄰信息，實現重疊區域樣本的檢測并提出了相應的重疊樣本清洗策略，其次通過樣本的分布信息對清洗后的樣本進行欠采樣，提升不平衡學習的性能。本文的主要貢獻如下：

（1）提出了一種能夠有效處理類別重疊的欠采樣方法。該方法提出了一種基于貝葉斯后驗概率的先清洗后欠采樣的策略。

（2）提出一種融合多數類全局密度信息和局部分布信息的樣本選擇方法，引入集成學習強化不平衡學習的性能。

（3）在43個不平衡數據集上和13種采樣方法的對比實驗，驗證了本文所提的考慮避免重疊的欠采樣思路的有效性。

1 相關工作

自SMOTE被提出以來，不平衡數據學習受到廣泛關注，涌現了大量基于SMOTE的衍生算法。如Han等人[15]提出的專注處于邊界區域的少數類樣本的Borderline-SMOTE策略；He等人[16]提出的專注于困難樣本的ADASYN策略；Bunkhumpornpat等人[28]提出的專注于安全區域樣本的Safe-Level-SMOTE策略；以及結合聚類技術來避免采樣過程中生成噪聲樣本或重疊樣本的LR-SMOTE[29]、GDDSYN[30]方法；引入過濾或清洗技術的混合采樣方法SMOTE-IPF[31]、SMOTE-Tomek和SMOTE-ENN[32]等。

與過采樣策略相對應的方法為欠采樣方法，它包括隨機欠采樣和有監督欠采樣。隨機欠采樣方法（RUS）是從多數類中隨機抽樣，被選中的樣本將被刪除直到數據集達到平衡為止。然而，該方法未考慮數據的實際分布情況，采樣具有隨機性，容易丟失樣本的重要信息。有監督欠采樣方法則需要預先設定好選擇標準，有目的地刪除多數類樣本來平衡數據分布。如何根據不平衡數據的分布信息選取多數類樣本來構建分類決策面成為此類方法的研究重點。

近年來，研究者們提出了許多智能的欠采樣方法。Wilson[33]提出的ENN根據K近鄰分類原則將錯分的多數類刪除，但由于大部分多數類樣本的局部區域分布的樣本多為同類樣本，導致ENN所能刪除的樣本十分有限。Ivan[34]提出的Tomek Links通過清洗數據來降低類間重疊，其主要思路是找到兩個類標簽不同且最近鄰互為對方的樣本，然后移除屬于多數類的樣本或兩者。Hart[19]提出使用1-NN的方法壓縮多數類的CNN方法。此外，Mani等人[35]提出了Near Miss利用多數類和少數類之間的距離關系剔除多數類樣本的一類方法。Smith等人[23]提出IHT方法，它是在訓練數據集上應用分類器，然后篩選掉概率低于閾值的多數類樣本。

然而，上述方法大多都是基于近鄰信息和隨機欠采樣的簡單規則，在處理復雜的數據時得到的分類效果往往不佳。基于聚類策略的欠采樣方法主要利用K-means算法將訓練數據集劃分為多個簇，然后從這些簇中挑選信息多數類樣本子集。如Lin等人[20]介紹了兩種聚類欠采樣策略。該方法先將所有的多數類樣本聚類為與少數類樣本等量的簇，然后提出利用簇中心來表示多數類和使用簇中心的最近鄰樣本代表多數類的兩種樣本選擇策略。然而，基于K-means的聚類方法容易受到噪聲和離群點的影響，當數據分布比較復雜時，這類方法并不可靠。

近年來，集成技術在欠采樣中得到了廣泛的應用，相關研究[13，36]表明欠采樣算法更適用于構建集成學習分類系統。基于集成的欠采樣方法通過在多個欠采樣數據集上訓練一組分類器，能夠在一定程度上減少多數類樣本的信息丟失問題，提高模型性能。集成欠采樣方法的典型代表有Seiffert等人[11]提出的RUSBoost及Liu等人[13]提出的EasyEnsemble和BalanceCascade等。

此外，現有研究表明當數據樣本單純在數量上不平衡時并不意味著這個數據就難以分類，而是在不平衡之外的其他因素[37]，比如噪聲、離群點、類重疊等也會影響模型的分類性能，而類的不平衡會進一步加劇這一問題。為此，出現一些針對不平衡數據中類重疊問題的相關研究[38-39]。

2 融合后驗概率和密度的不平衡數據欠采樣方法

本章主要介紹基于貝葉斯后驗概率的欠采樣方法BPDDUS。BPDDUS的工作原理主要由以下三部分組成：首先，清洗多數類中的噪聲和重疊樣本；然后，對處理后的多數類樣本分配權重；最后，根據多數類樣本的采樣權重隨機采樣并構造多個基分類器，集成訓練。

為描述方便，這里先給出一些形式化的描述：Dtrain=Dmaj∪Dmin，Dtrain表示給定的不平衡訓練集，Dmaj表示多數類樣本集，Dmin表示少數類樣本集。N=Nmaj+Nmin，N為訓練集樣本數量，Nmaj為多數類樣本數量，Nmin為少數類樣本數量。X∈Dtrain∧X=(x1,x2,…,xm)，X表示一個m維的樣本，xi表示樣本的第i個特征值。Y={y1,y2}，Y表示樣本的標簽，其中y1為多數類標簽，y2為少數類標簽。

2.1 多數類樣本的清洗

對重疊區域的多數類樣本進行處理能夠有效提升不平衡數據的分類效果，本文提出的方法通過對樣本局部信息學習，根據樣本局部分布特征對多數類樣本進行清洗，避免選擇的多數類樣本子集中還存在高重疊樣本。目前，挖掘局部信息的方法有很多，最經典的是基于KNN的方法，已經廣泛應用于許多學習算法中，比如SMOTE、MWMOTE等。

此外，分類決策實質上是通過將待識別樣本的特征空間劃分成多個決策區域，然后根據樣本的特征向量位于哪個決策區域來判斷它屬于哪一類別。貝葉斯決策論是概率框架下實施決策的基本方法。對分類任務來說，在所有相關概念都已知的理想情形下，貝葉斯決策論考慮如何基于這些概率和誤判損失來選擇最優的類別標記[40]。在這里，利用貝葉斯后驗概率的KNN估計來獲取多數類樣本的局部信息，并依據樣本的局部信息來識別多數類樣本中的噪聲、重疊樣本以及信息樣本。其中，貝葉斯后驗概率的K近鄰估計公式如下：

其中，BPi表示待測樣本Xi屬于Y的概率，K表示Xi的最近鄰樣本數量，NK_Y表示Xi的K個近鄰中同類樣本的數量。基于式（1）來計算訓練集中每個多數類樣本屬于多數類的后驗概率，得到式（2），且Xi∈Dmaj，1≤i≤Nmaj。

本文提出的方法首先利用式（2）計算每個多數類樣本屬于多數類的后驗概率，然后根據概率值大小篩選信息多數類樣本。

從總體上來看，隨著BPi的增大，樣本的安全水平也在增大。然而，對于BPi＜1 2的樣本，它們的重疊程度較高，周圍分布了較多的異類樣本。這些樣本大概率為噪聲或重疊樣本，對后續的模型訓練會產生不利影響。相反，對于BPi≥1 2的樣本，這些樣本是靠近決策邊界或位于多數類樣本的密集區域或邊緣區域的信息樣本，相對比較安全。尤其是那些靠近邊界的邊緣樣本，它們攜帶了分類的重要信息，這類樣本有助于提升模型的分類性能。為了增強分類邊界的可分性，提升后續不平衡數據的學習性能，將BPi＜1 2的多數類的采樣權重設置為0，以避免噪聲樣本或高度重疊區域中的多數類樣本參與后續的模型訓練。

如圖1，圓圈表示多數類樣本，四角星表示少數類樣本。為了更好地描述多數類樣本的局部情況，以圖1（a）～（b）中多數類樣本A、B、C分別描述噪聲樣本、重疊樣本以及信息樣本（最近鄰數量為5）。其中，圖1（a）中樣本A深入少數類內部，其周圍分布的全為少數類樣本，后驗概率BPA=0；圖1（b）中的樣本B靠近少數類群，其后驗概率BPB=2 5，這類樣本的類別不確定性最大，不僅會影響其周圍少數類樣本的識別，還會模糊類決策邊界，增加類不平衡問題的學習難度。圖1（c）中的樣本C遠離少數類群，其后驗概率BPC=1，這類樣本對于不平衡數據的分類模型有著重要的作用。

圖1 不同類型的多數類樣本示意圖Fig.1 Different types of majority samples in imbalanced data

2.2 多數類樣本的加權

在2.1節中，本文利用貝葉斯后驗概率的K近鄰估計剔除不平衡訓練集中潛在的噪聲點和重疊度較高的多數類樣本，如圖2（a）黑色實心圓為被剔除的樣本，空心圓為信息樣本。接下來，將對剩余的信息多數類樣本做進一步分析，根據不平衡數據的分布特征來評估不同樣本對分類的重要程度并依此為其分配相應的采樣權重。

根據信息多數類樣本在輸入空間的初始分布情況可以把樣本劃分為三種類型：第一種為靠近分類邊界的邊緣樣本，即內邊緣樣本；第二種為處于多數類內部區域的高密度樣本，即中間樣本；第三種為遠離分類決策邊界、遠離中間樣本的外邊緣樣本。如圖2（b），黃色實心圓為內邊緣樣本，紅色實心圓為中間樣本，藍色實心圓為外邊緣樣本。在這三類樣本中，中間樣本的密度最大，內邊緣樣本和外邊緣樣本的密度相對較小。另外，遠離邊界的中間樣本和外邊緣樣本冗余度較大，能夠提供的信息比較有限，它們所攜帶的信息分類器可以從其他樣本中獲得。相比之下，內邊緣樣本能夠提供更多的有用信息，對提升模型的學習性能有著重要的作用。如果僅考慮樣本的密度進行采樣，那么中間樣本就會采得多，其他樣本少。雖然當前已有基于密度的采樣方法[30]，但是單用密度在某些情況下并不能很好地度量樣本之間的差異性。如圖2（b）中的Part1和Part2區域中的樣本，這些樣本的密度雖然相同，但是它們距離分類決策面的距離是不一樣的。Part2區域中的樣本比Part1區域中的樣本距離決策面更近，對分類的貢獻程度更大，得到的采樣權應該更大。因此，為了更好地度量樣本對不平衡學習的重要程度，引入了信息熵來進一步刻畫樣本之間的差異。其中，樣本離分類決策面越近，熵值就越大。綜合考慮樣本的全局密度和樣本的信息熵來評估樣本對分類的重要性。這里給出以下公式來計算樣本的全局密度、信息熵以及多數類樣本的采樣權重：

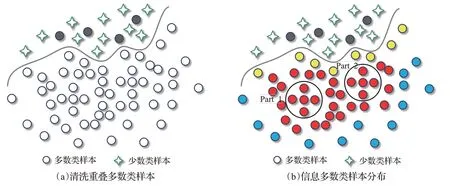
圖2 信息多數類樣本的空間分布圖Fig.2 Spatial distribution of informative majority samples

式（3）為基于高斯核的全局密度計算公式，?Xi,Xj∈Dmaj，i≠j，Di表示樣本Xi的全局密度，dc表示截斷距離表示樣本Xi和Xj之間的歐氏距離，ω為比例因子。式（4）為伯努利分布熵計算公式，Ei表示多數類樣本的信息熵值。式（5）為樣本的權重wi計算公式。為了消除量綱的影響，在獲得樣本的采樣權重后對其進行規范化處理。

2.3 集成學習模型的構建

通過2.1節和2.2節對訓練數據集進行預處理并按采樣權重無放回地隨機抽取Nmin個信息多數類樣本，結合少數類樣本以獲取一個平衡分布的數據集。這雖然在一定程度上能夠減少關鍵多數類樣本的信息丟失，但若數據中少數類的絕對數量很少時，欠采樣很容易由于訓練數據不足，出現欠擬合現象，導致分類性能變差，同時樣本的信息丟失問題仍無法有效解決。為此，集成學習策略被廣泛應用于不平衡數據集的欠采樣中，通過構建集成學習系統能夠有效地緩解多數類樣本的信息丟失問題，同時提升后續模型的泛化能力。

本文結合加權隨機采樣和并行集成方法來構造不平衡數據的集成分類學習模型。其中，并行集成方法的主要原理是利用不同基分類器之間的差異性，通過各分類器的投票結果來降低分類錯誤。具體實現過程如下：

（1）構建單個基分類器：對多數類樣本按權重無放回地隨機抽取與少數類等量的樣本，并結合所有少數類樣本構建基分類器。

（2）形成集成學習系統：對訓練集重復執行步驟（1）來構建一組基分類器，并將獲取的基分類器用于bagging集成學習。

（3）結合所有基分類器的預測值，由相對多數投票決定最終的分類結果。

本文方法先通過貝葉斯后驗概率來清洗重疊樣本，然后根據全局分布密度和信息熵為信息樣本設置權重，并依此按權隨機欠采樣，最后構建集成學習系統.算法的具體步驟如下：

算法1融合后驗概率和密度的不平衡數據欠采樣方法（BPDDUS）

輸入：不平衡訓練集Dtrain，近鄰數量K，比例因子ω，基分類器數T。

3 實驗設計與分析

為了驗證所提算法的有效性，本文采用KEEL數據庫（http：//www.keel.es）中的二分類不平衡數據集進行對比實驗。

3.1 數據集

本文基于KEEL數據集庫中的100個不平衡數據集進行實驗研究。考慮到KEEL中的一些數據集都是來自同一原始數據的分解變換，為此對數據集進行了篩選。首先，選擇所有未重復的數據集；然后，對于重復的數據集選擇不平衡率最高和次高的數據集；最后，對剩余的數據集，選擇少數類樣本數量少于10個的數據集。通過上述的方法得到43個數據集。表1給出了選定數據集的詳細信息。其中，IR表示數據的不平衡率，OR表示類間的重疊程度[41]，m表示樣本的屬性個數，N表示訓練集樣本的數量，Nmaj表示多數類樣本的數量，Nmin表示少數類樣本的數量。數據集按IR從小到大排列，這些數據集的IR范圍為1.86～129.44，OR范圍為0～0.99。

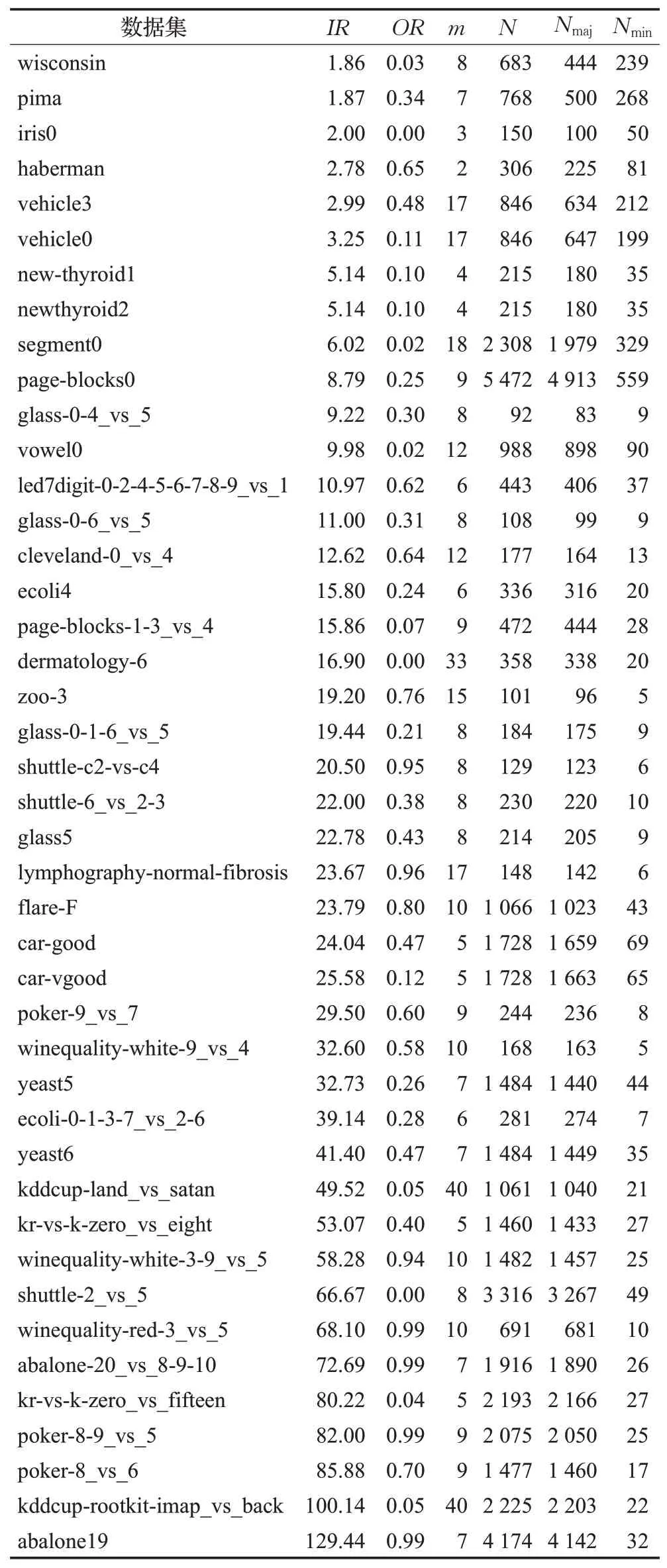
表1 43個KEEL數據集的詳細信息Table 1 Details of 43 KEEL datasets

3.2 性能指標

目前比較常用的分類器的評價指標主要有準確率（Accuracy）、精確率（Precision）、召回率（Recall）、F1-score、G-mean以及AUC。其中，準確率為分類正確的樣本占總體樣本的百分比，它是分類問題中最簡單、直觀的評估指標，但存在著明顯的缺陷。當處理不平衡數據的問題時，準確率不能客觀評價學習算法的好壞；Precision又稱查準率，針對樣本最終的分類結果而言，在所有被分類為少數類的樣本中實際為少數類的樣本的概率，表示對少數類樣本的預測準確程度；Recall又叫查全率，針對實際樣本而言，在實際為少數類的樣本中被分類為少數類樣本的概率。F1-score是Precision和Recall的加權調和平均值，是Precision和Recall的綜合指標，F1-score越高，學習模型就越穩健；G-mean是反映了分類器對整體分類性能的評估指標，只有當少數類和多數類的識別率都比較高時，G-mean就較高；AUC則是ROC曲線[42]下的面積，AUC值越大，模型的分類效果越好。因此，本文以AUC、G-mean和F1-score作為性能的評估指標。

3.3 參數分析

BPDDUS算法主要參數：（1）K用于挖掘多數類樣本局部信息的最近鄰數量；（2）ω用于計算多數類樣本全局密度的比例因子；（3）T集成訓練的基分類器數量。對于KNN近鄰估計K參數，如果取值過小容易產生方差較大的估計，然而K值過大則會產生偏移估計，所以在這里將K設置與SMOTE算法中近鄰參數相同，即K=5。在本節中進行了兩組實驗分別研究ω和T對BPDDUS算法的分類性能影響，由于高斯徑向基核函數具有較強的局部性，參數ω決定了該函數的作用范圍，隨著ω的增大其局部感知能力會減弱。在這里，將ω的域值設定在[1%，2%，3%，4%，5%]。為了節省空間，從表1中隨機選取5個IR不同級別的數據集替代選定的所有數據集進行實驗，它們分別為wisconsin、flare-F、yeast6、poker-8_vs_6和abalone19，對應的IR分別為1.86、23.79、41.40、85.88、129.44。如表2為不同ω下BPDDUS在三個指標下的性能值。

表2 不同ω下BPDDUS的性能值Table 2 Performance values of different ω on BPDDUS

根據表2中的對比結果可知：（1）同一數據集在不同ω下BPDDUS的性能差距不明顯，說明BPDDUS算法對參數ω的敏感度比較小，分類性能比較穩定。（2）較小的數據集在ω為1%～2%分類效果相對更好，較大的數據集在ω為4%～5%效果更好。對于集成訓練參T，研究T分別在[1，5，10，20，30，40，50]下與BPDDUS算法性能的關系。如圖3為BPDDUS隨T的改變下的AUC值。從圖中可以看出，隨著T的增大，模型的分類性能逐漸升高，特別是在基分類器從1～5時效果明顯。同時，對IR較小的數據集wisconsin，T值的改變對BPDDUS算法性能變化不明顯，而對IR較大的數據集poker-8_vs_6和abalone19在T由1增大到20這一階段，BPDDUS算法性能提升比較明顯，在T為30～50時BPDDUS在這5個數據集上的性能較穩定。從上述實驗結果可以進一步說明集成學習的重要性，對于不平衡率較高的數據集，可以通過增加基礎學習器來提升模型的分類性能。

圖3 不同T下BPDDUS的AUC值Fig.3 AUC values of BPDDUS at different T values

3.4 結果分析

為了防止在訓練過程中出現過擬合問題，同時確保訓練集和測試集的類間比例與原始數據一致，本文采用5折分層交叉驗證法進行實驗。每次實驗運行10次，實驗結果取10次5交叉的AUC、G-mean和F1-score均值以避免實驗的隨機性對結果產生影響。本文將BPDDUS（簡寫為BPUS）算法與13種采樣方法進行比較，分別為：ClusterCentroids（CC）、NearMiss（NM）、ENN、TomekLinks（TL）、SMOTE+Tomek（ST）、SMOTE-IPF（SI）、RUS、EasyEnsemble（EE）、RUSBoost（RB）、CNN、AdaCost（AC）、IHT、RBU。這13種算法均來源于imblearn庫。為了保證實驗的公正性，所有實驗均以CART決策樹為基分類器，對比算法的所有參數均為默認參數。

同時，為了更直觀地分析實驗結果，將BPUS與不同算法在43個不平衡數據集上的AUC、G-mean和F1-score的對比結果整理為圖4～6。圖中深藍色的部分“DN+”表示在當前性能指標上，BPUS性能值大于其他對比方法的數據集數量，淺藍色部分“DN=”表示BPUS與其他方法的性能值相同的數據集數量，黃色部分“DN-”表示其他方法性能值大于BPUS的數據集數量。從圖4和圖5可以看出在指標AUC、G-mean上BPUS與其他方法相比至少有20個數據集表現更優，尤其是與CC、NM、RUS、RBU相比本文的BPUS算法優勢更加明顯。由圖6可知，本文所提方法盡管在F1-score上超過了5種算法，但整體而言，相對表現不佳。尤其是和SMOTE+Tomek、SMOTE-IPF的表現差距較大，這一結果與文獻[18]的結果一致，其可能的原因是：一方面過采樣方法能夠提供更多的安全樣本和更低比例的危險樣本；另一方面，當數據集中少數類樣本較少時，在交叉驗證的訓練過程中訓練集由于缺乏少數類數據的支撐，而導致對少數類樣本的識別精度偏低，這可能是另一個方面的原因。

圖4 對比實驗指標AUC結果Fig.4 AUC results of comparative experiment

圖5 對比實驗指標G-mean結果Fig.5 G-mean results of comparative experiment

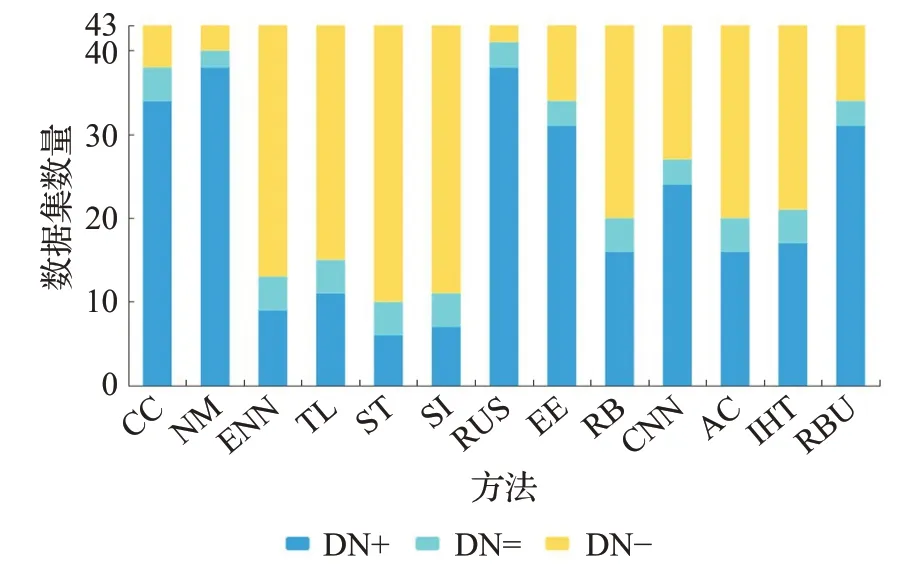
圖6 對比實驗指標F1-score結果Fig.6 F1-score results of comparative experiment

為了進一步驗證BPUS算法的有效性，本文對上述13種對比算法和BPUS算法進行無參的顯著性統計假設檢驗，在這里使用雙因素秩方差分析（Friedman檢驗），表3為所有算法在選定的不平衡數據集上Friedman檢驗的統計量結果，其顯著性水平α=0.05，檢驗服從統計量為22.36，FF(1 3,546)為1.74。從表中可以看出AUC、G-mean和F1-score下和FF均大于和FF(1 3,546)，p值遠遠小于0.05，這說明在0.05的水平上應該拒絕原假設，認為這14種算法的分類效果不一樣。

表3 14種算法在43個數據集上的Friedman檢驗統計值Table 3 Friedman test statistics of 14 algorithms on 43 data sets

同時利用Friedman檢驗得到了不同算法在43個數據集上三個指標的平均優劣排名次序，見圖7～9。其中，算法的性能越好，排名就越靠前。在圖7～9中離圓的中心點越近表明算法表現就越好，反之，離圓的中心點越遠或者離圓的邊界越近算法性能就越差。從圖7～9中可以看出本文提出的方法在AUC和G-mean上明顯優于其他算法。具體來說，在AUC上表現最好的三個算法為BPUS、EasyEnsemble和IHT，其平均排名次序分別為4.3、5.38、5.78，較差的為平均排名為10.6、10.2、9.23的NM、RBU和CNN算法。同理，在G-mean上可以得出相似的結論，性能最好的三個算法仍然為BPUS、EasyEnsemble和IHT，較差的為NM、AdaCost、CNN算法。在F1-score上表現較優的為SMOTE+Tomek、SMOTE-IPF、ENN和TomekLinks，IHT、AdaCost和BPUS表現居中，RBU、CC和NM表現最差。

圖7 14種算法的AUC平均排名次序Fig.7 Average AUC ranking of 14 algorithms

圖8 14種算法的G-mean平均排名次序Fig.8 Average G-mean ranking of 14 algorithms

圖9 14種算法的F1-score平均排名次序Fig.9 Average F1-score ranking of 14 algorithms

綜上所述，本文提出的方法在43個KEEL不平衡數據上總體分類效果較好，尤其是在指標AUC和G-mean表現優異，這說明BPDDUS算法能夠有效地加強分類器對關鍵多數類樣本的重視，減少了重要信息的丟失。同時也證實了在進行欠采樣時考慮樣本的空間分布及局部信息的必要性和重要性。

4 結語

本文提出了一種基于貝葉斯后驗概率的多數類集成欠采樣方法，該方法利用貝葉斯后驗K近鄰估計充分挖掘多數類樣本的局部信息，根據樣本的空間分布盡可能準確地選取能夠映射分類信息的重要樣本，以提高后續模型訓練的質量。通過與13種算法在43個數據集上的對比實驗結果表明，BPDDUS是一種有效的不平衡數據預處理方法。另外，Friedman檢驗也證明了BPDDUS與13種經典采樣方法存在顯著性的差異，尤其在AUC和G-mean指標上，本文方法明顯優于其他方法。

盡管如此，BPDDUS也存在一定的局限性。當數據集中少數類樣本較少時，有限的少數類樣本能夠提供的信息十分有限，此時僅靠增加集成訓練次數無法有效地提升性能。因此，如何在此類少數類樣本極少的情況下，提升不平衡數據的學習性能值得進一步的研究。