空氣懸架客車橫向動力學建模和穩定性分析*

陳 龍，陳 明，孫曉強，蔡英鳳，Pak Kin Wong，吳子強

（1.江蘇大學汽車工程研究院，鎮江 212013；2.澳門大學機電工程系，澳門 999078；3.揚州市奧特瑞汽車電子科技有限公司，揚州 225299）

前言

客車由于質量大、質心高、輪距窄等特點，其在高速緊急避撞（高速大轉角）和濕滑路面轉向等特殊行駛工況下極易產生橫向失穩現象［1］。該現象若不能實現準確揭示和預判，最終將會導致客車發生側翻事故。懸架是研究客車橫向運動必須考慮的關鍵因素之一［2］。隨著客車技術的快速發展，裝備空氣懸架已成為主流趨勢。相較于傳統懸架，空氣懸架能夠顯著提升客車綜合性能，但空氣懸架客車的橫向運動演化過程與傳統懸架客車存在明顯差異，系統非線性特征更為明顯，橫向穩定性分析難度更大、挑戰更高［3］。

構建能夠準確反映空氣懸架客車橫向動力學演化規律的數學模型，是后續進行系統穩定性分析的基礎。Gauchia等［4］建立了一種用于估計客車側翻運動過程中橫向加速度閾值的數學模型。Altork等［5］為實現客車橫向穩定性控制，建立了考慮橫擺、側傾和橫向運動的客車3自由度動力學模型。付翔等［6］以四輪轉向2自由度模型為基礎提高了四輪轉向車輛在低附路面的穩定性。王睿等［7］建立了基于橫向載荷轉移率的客車7自由度動力學模型，分析了結構參數及車速對客車側翻穩定性的影響。然而，針對客車相關部件在大范圍運行工況下的非線性力學行為，現有研究仍缺乏有效的建模方式。

當前，無論是客車還是其他類型車輛，關于橫向穩定性分析的內容主要集中在橫向失穩指標確定。Brennan等［8］提出基于零力矩點的汽車橫向失穩指標。Zhang等［9］基于相平面法研究了車輛側翻穩定性，提出了基于載荷轉移比等高線的車輛側翻指標。黃明亮等［10］采用能量法來研究汽車側翻穩定性，提出了新的汽車側翻能量穩定指標。葉慧等［11］通過對質心側偏角的估計和傳感器獲得橫擺角速度的方法，利用一種非光滑控制技術提升了車輛的橫向穩定性。然而，由于特殊行駛工況下的客車橫向運動過程較為復雜，系統非線性特征明顯，因此單一失穩指標因缺乏對車輛全局動態的綜合考慮，往往無法準確全面地評估客車實際側翻過程。

針對以上問題，本文在考慮空氣彈簧及輪胎非線性力學特性的基礎上，首先建立空氣懸架客車3自由度非線性橫向動力學模型，進而運用非線性系統穩定性分析理論，對空氣懸架客車在高速轉向等特殊行駛工況下的橫向穩定性進行鞍結分岔分析，獲取空氣懸架客車的橫向動力學失穩演化規律，最后通過整車動力學仿真對穩定性分析結果進行驗證。相關研究能夠為提高客車橫向行駛安全提供一定依據。

1 客車橫向動力學模型

1.1 整車橫向動力學模型

結合空氣懸架客車的結構特點和系統穩定性分析需求，建立考慮空氣彈簧和輪胎非線性力學特性的空氣懸架客車3自由度非線性橫向動力學模型，主要包括車身橫向運動、側傾運動和橫擺運動，模型結構如圖1所示。

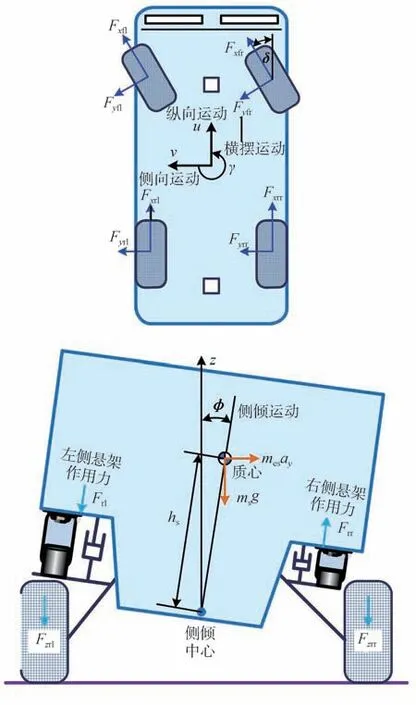
圖1 空氣懸架客車3自由度橫向動力學模型

基于牛頓運動定律，模型具體表達式如下。

（1）橫向運動模型

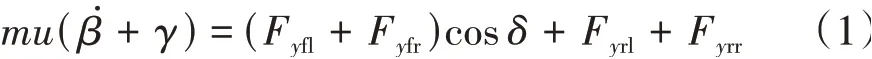
（2）橫擺運動模型

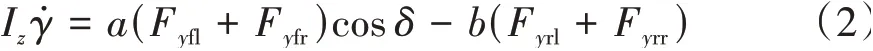
（3）側傾運動模型

式中：m為整車質量；ms為簧上質量；β為車身質心側偏角；φ為車身側傾角；γ為車身橫擺角；δ為前輪轉角；Ix為車身側傾轉動慣量；Iz為車身橫擺轉動慣量；a、b、d分別為質心到前后輪的距離及輪距；hs為車身側傾中心高度；Fyi為輪胎側偏力；Fi為空氣懸架對車身的垂向作用力（i=fl，fr，rl，rr）。Fi的表達式為

式中：ki（t）為空氣彈簧的時變剛度；ci為空氣懸架減振器的阻尼系數；Δs為懸架相對位移。

1.2 空氣彈簧非線性模型

作為空氣懸架的主要彈性元件，空氣彈簧具有典型的非線性剛度特性，且該剛度特性與彈簧被壓縮或被拉伸的程度直接相關［12］。本文以膜式空氣彈簧為例，對空氣彈簧動剛度特性進行分析，可得空氣彈簧彈性力的表達式為［13］

式中：F為彈性力；pa為大氣壓力；p為氣囊內氣體絕對壓力；pe為氣囊內氣體相對壓力；Ae為空氣彈簧有效截面積。空氣彈簧剛度可通過彈性力直接對空氣彈簧垂向位移求導得到：

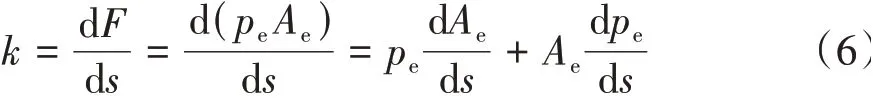
式中：k為空氣彈簧剛度；s為空氣彈簧垂向位移。假設空氣彈簧氣囊內的氣體總質量一定，則壓力和容積的關系可表示為

式中：V為氣囊容積；n為氣體多變指數，1≤n≤1.4。式（7）兩邊分別對s求導，可得：

那么氣囊內氣體相對壓力對s求導可得：

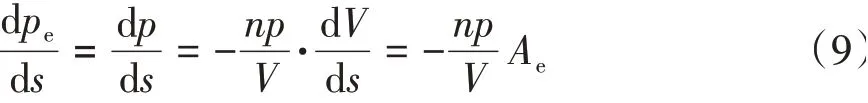
式中負號表示壓力變化趨勢與體積變化趨勢相反，表示剛度時，取其絕對值。

綜合上述各式，空氣彈簧剛度的表達式為

對于活塞座為圓柱形的膜式空氣彈簧，其有效面積在工作行程內的變化可忽略不計［14］，則空氣彈簧的非線性剛度特性可進一步簡化為

1.3 輪胎非線性模型

在車輛動力學分析過程中，大多采用“魔術公式”或Dugoff等經驗輪胎模型反映輪胎力的強非線性特征［15-16］。然而，在解析分析過程中，這些輪胎模型形式較為復雜，可能導致解析問題無法求解。因此，為便于理論推導和后續問題解決，同時考慮到高速轉向時輪胎側向力與垂直載荷的非線性關系，本文選用較為簡潔的多項式平方輪胎模型［17］，其表達式為

式中：i=fl，fr，rl，rr，j=f，r；Fyi為輪胎側向力；Fzi為輪胎垂向載荷；Ci為輪胎側偏剛度；Cj1、Cj2為經驗常數；αj為輪胎側偏角；μ為路面附著系數。

前后輪胎側偏角的表達式為

車輛在橫向運動過程中，載荷將發生橫向轉移，輪胎垂直載荷的變化可表示為

其中

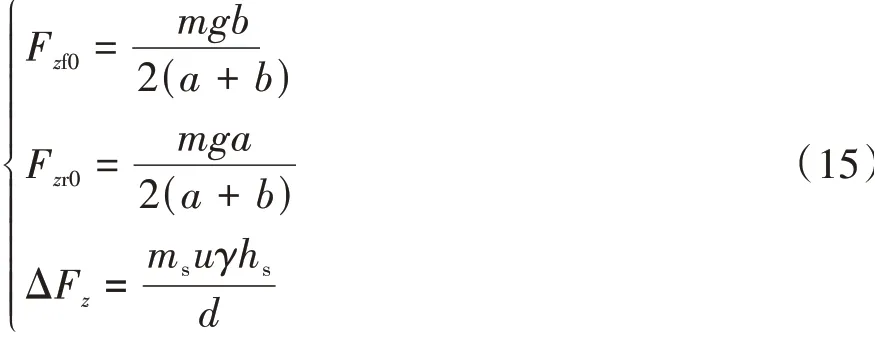
式中：Fzfo和Fzro為前后輪垂向靜載荷；ΔFz為表示前后輪的載荷轉移量。

2 非線性系統穩定性分析

2.1 非線性微分動力學系統的建立

為構建空氣懸架客車橫向動力學系統微分形式，將車輛縱向速度、前輪轉角和附著系數定義為輸入參數ξ，令φ?=η，（β，γ，φ，η）T表示為（x1，x2，x3，x4）T，則式（1）～式（3）可寫成如下非線性動力學系統的微分形式：

式中：X=（x1，x2，x3，x4）T為系統狀態變量；ξ=（u，δ，μ）T為系統可變參數。則上式可表示為其中：

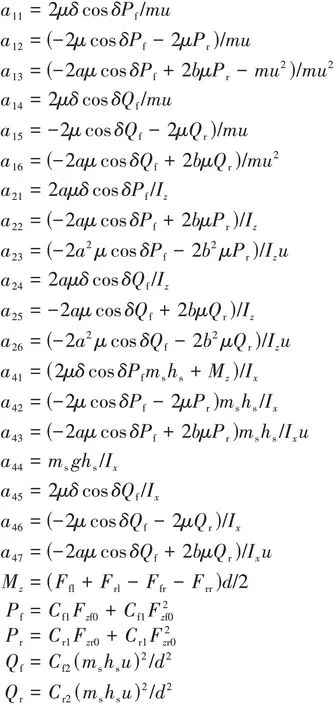
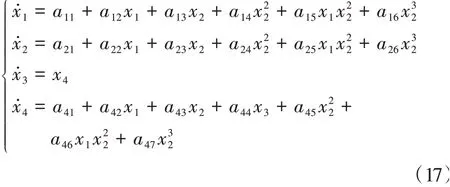
令式（16）等式左端等于零，可求得非線性系統的平衡點，設此平衡點為Xe=（xe1，xe2，xe3，xe4），同時可得到此系統在平衡點處的雅克比矩陣J為

矩陣J的特征方程為

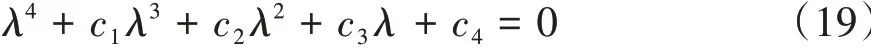
式中：系數ci（i=1，2，3，4）與矩陣J的元素有關，具體數學關系為

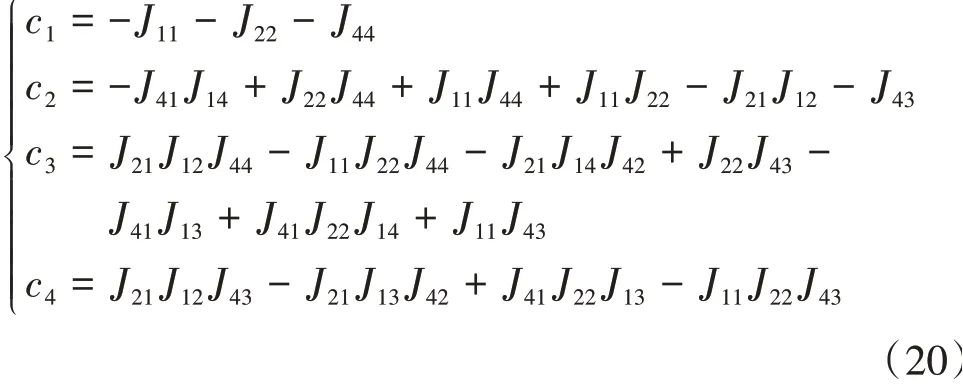
根據非線性系統穩定性Hurwitz判據，若以下條件滿足：

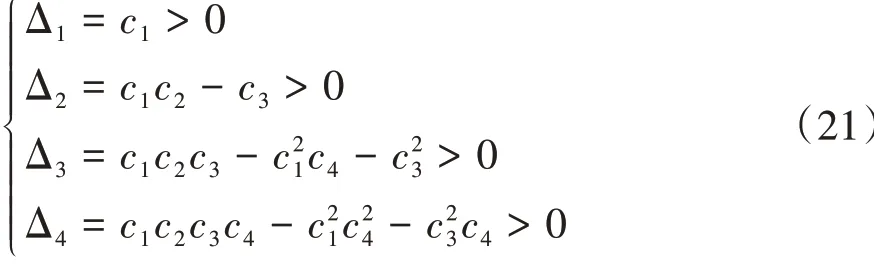
則特征方程的特征根均具有負實部，非線性系統在平衡點時漸近穩定的；若式（21）不成立且c4≠0，那么特征方程存在正實部特征根，說明系統的平衡點是不穩定的。當c4=0時，特征方程具有含零實部的特征根，此時平衡點鄰域處于一種臨界狀態，具有非常復雜的非線性動力學行為。此時平衡點附近的線性化系統不一定和原系統拓撲等價，因此，需要對系統進行降維，通過降維后的約化系統分析原系統在平衡點的非線性動力學行為［18］。

2.2 基于中心流形理論的系統降維

對于存在各種非線性因素的復雜高維動力學系統，通過降維進行分岔分析可為其控制設計提供理論依據。基于中心流形理論的降維方法基本思想是：假設在平衡點附近的系統存在有限維中心子空間，根據中心流形定理，可將方程向中心子空間投影，從而達到降維目的［19］。

設路面附著系數μ和車速u為定值，隨著前輪轉角δ的增加，車輛轉向時一定會出現奇異點（X*，δ*），也即式（19）一定會出現c4=0的情形。將奇異點坐標變換轉移到原點，令：

則系統可轉換為奇異點在（0，0）處的微分方程：

在此奇異點（0，0）處，穩定性條件式Δ4=0，則式（22）存在1個零特征根和3個實部為負數的特征λ1、λ2和λ3。構造一個矩陣M，其列為A的零特征根和負實部特征根對應的特征向量。取T=M-1，則有：

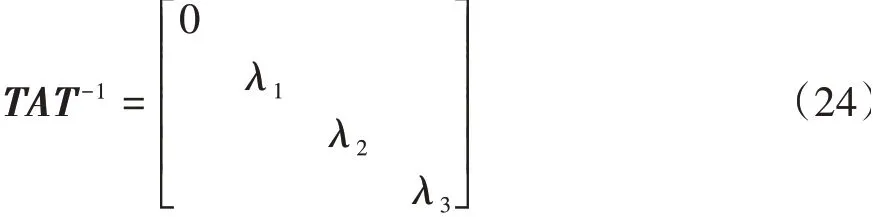
則式（23）可變換為

式中：Y為變換后的狀態變量；Λ為由A的特征值組成的對角矩陣。將變量分為臨界狀態Yc和穩定狀態Ys，其中Yc=y1，Ys=（y2，y3，y4）T，則式（26）可分解為

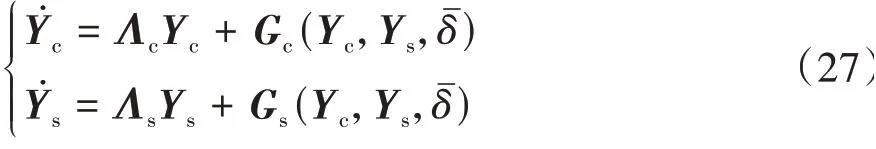
式中Λc=0，Λs=diag（λ1，λ2，λ3）。

對于式（27），由中心流形定理有，當Λc的所有特征值為零，Λs所有特征值實部為負，那么存在一個可微函數H，使得Ys=H（Yc），且其為式（26）的中心流形，具體函數關系可表示為

其邊界條件為

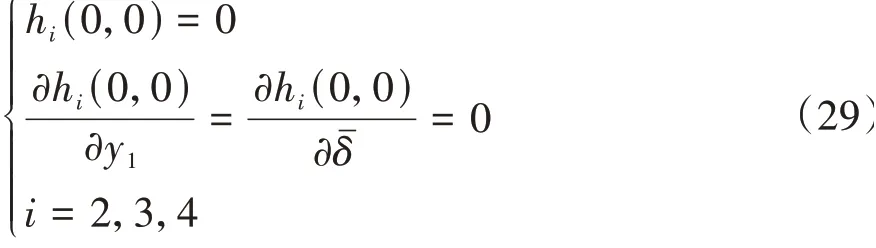
在此基礎上，中心流形方程為

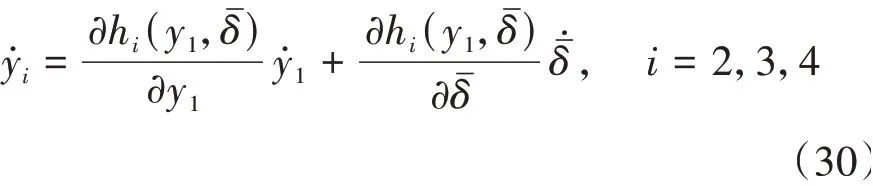
設hi（y1，δ），則可展開為如下形式。

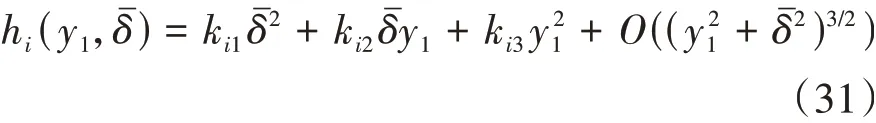
將式（31）代入式（26），通過對比可求得ki1、ki2、ki3（i=2，3，4）的具體數值和中心流形，再將其代入式（27）的第1式可得中心流形上的約化系統。將車輛參數，如表1所示，進一步代入系統，求其約化系統具體表達式為

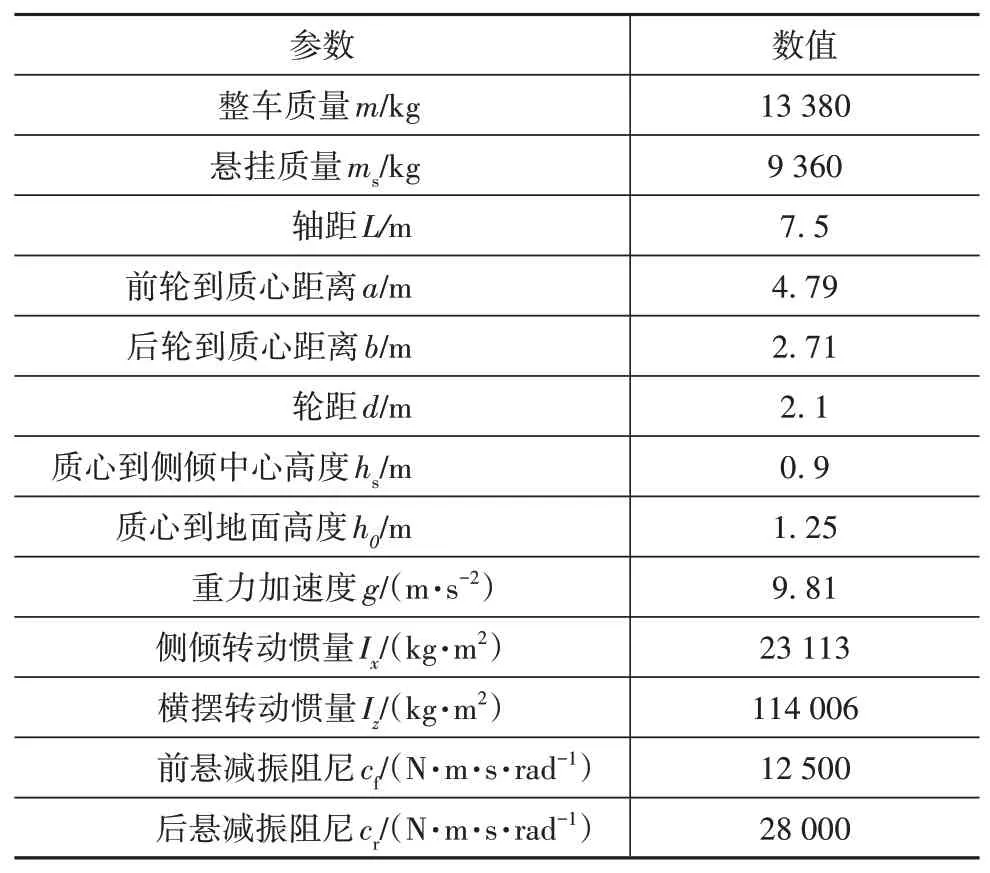
表1 整車主要參數

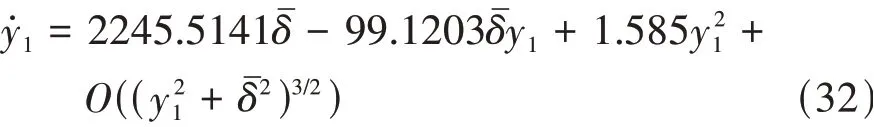
定理1：在確定系統中心流形條件下，如果降階系統的原點是漸進穩定的（或非穩定的）則整個系統的原點也是漸進穩定的（或非穩定的）［19］。

式（32）就是式（26）在奇異點附近的約化系統，由定理1可知其與原方程相比，定性性態是等價的，因此，求原方程的定性性態只需對約化后的系統進行定性性態分析。

2.3 系統鞍結分岔判定

對于一維含參數的非線性動力學系統

式中：x為狀態變量；θ為分岔參數。當θ＜0時，系統無平衡點；當θ＞0時，系統有兩個平衡點，x1=θ1∕2，x2=-θ1∕2。平衡點x1=θ1∕2的雅克比矩陣Dxf（x1，θ）=-2θ1∕2＜0，則x1稱為穩定平衡點或結點，平衡點x2=-θ1∕2的雅克比矩陣Dxf（x2，θ）=2θ1∕2＞0，x2稱為不穩定平衡點或鞍點。所以x=0，θ=0為系統的分岔點，此分岔現象也叫鞍結分岔。非線性系統（33）在分岔點（0，0）有：

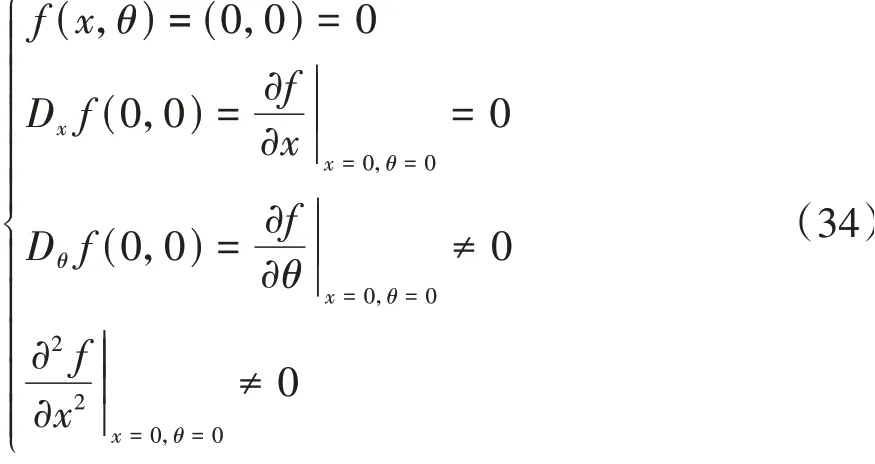
按此思路可以推出一維含參數的非線性動力學系統發生鞍結分岔的充分必要條件為［20］

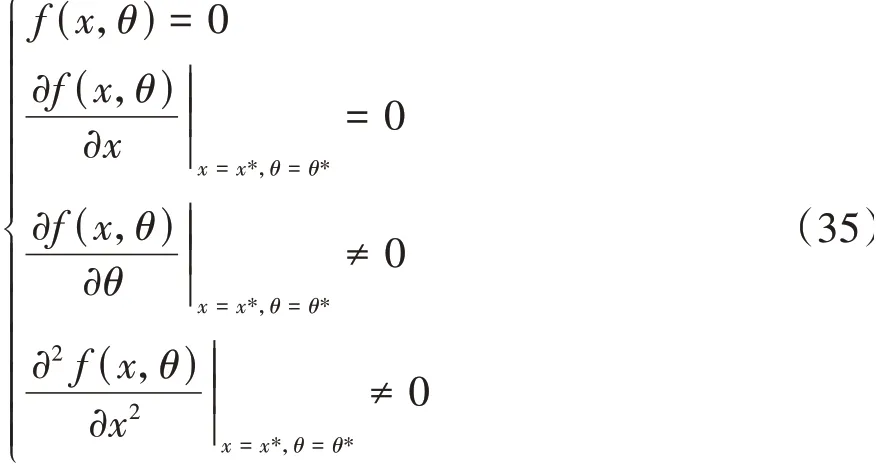
那么對基于中心流形定理降維后的約化系統式（32）進行分析可得：

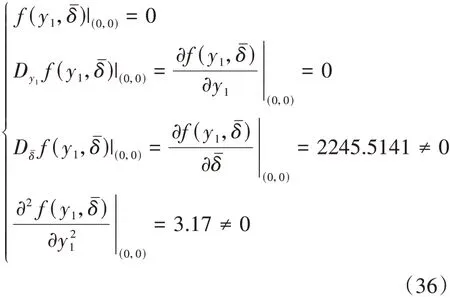
因此，式（16）滿足鞍結分岔的充分必要條件，系統將會發生鞍結分岔。

2.4 平衡點分岔行為分析

考慮到計算繁雜以及篇幅有限，本文僅以典型客車（表1）為對象進行分析，根據車輛實際運行狀態，設計4種工況進行系統穩定性分析，即掌握空氣懸架客車的橫向穩定性演化規律。工況1和工況2設置附著系數μ=0.8的高附路面，車速分別為72和108 km∕h，工況3和工況4設置附著系數μ=0.3的低附路面，車速分別為50和80 km∕h。通過分析計算，得到4種工況下車輛橫向穩定性鞍-結分岔相平面圖，如圖2～圖5所示，其描述了系統從初始狀態到失穩的變化過程。

圖2～圖5中結點為穩定平衡點，鞍點為不穩定平衡點。結點附近區域的相軌跡會收斂至穩定的平衡點，因此該區域為穩定區域，鞍點附近區域的相軌跡是發散的，表示為不穩定區域。

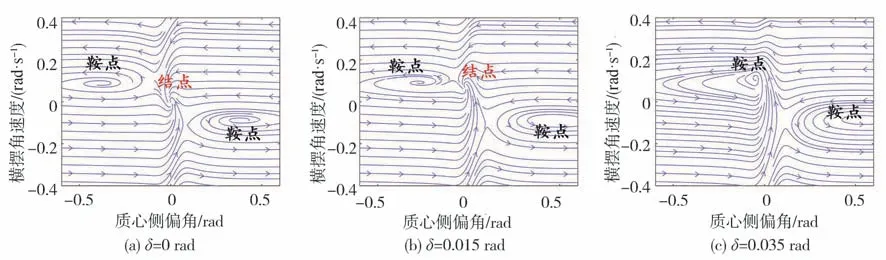
圖5 工況4相平面圖

由圖2和圖3可見：圖（a）中前輪轉角等于0時，穩定平衡點與原點是重合的，表明初始值位于穩定區域時，車輛收斂于直線運動；圖（b）中當前輪轉角分別增大到0.05和0.025 rad時，穩定的平衡點逐漸靠向一個不穩定的平衡點，穩定區域也因此逐漸減小；圖（c）中前輪轉角分別增大到0.098和0.052 rad時，兩平衡點無限接近，若轉角繼續增大，穩定平衡點將消失，系統只剩兩個不穩定的平衡點，此時系統穩定區域消失，處于任意初始值的車輛都將失穩。相較而言，速度更高的工況，系統趨向失穩的前輪轉角閾值較小。

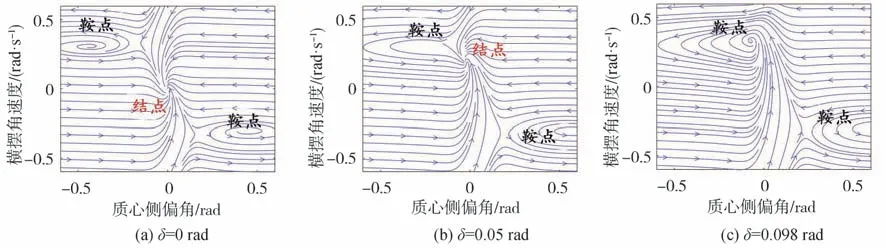
圖2 工況1相平面圖

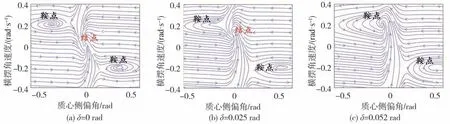
圖3 工況2相平面圖

由圖4和圖5可見：圖（a）中前輪轉角等于0時，穩定平衡點與原點是重合的，表明初始值位于穩定區域時，車輛收斂于直線運動；圖（b）中，當前輪轉角分別增大到0.03、0.015 rad時，穩定的平衡點逐漸靠向一個不穩定的平衡點，穩定區域逐漸減小；圖（c）中，前輪轉角分別增大到0.059、0.035 rad時，兩平衡點無限接近，若轉角繼續增大，穩定平衡點將消失，系統只剩兩個不穩定的平衡點，此時系統穩定區域消失，任意初始值條件下車輛都將失穩。通過比較后兩圖和前兩圖，可以發現，低附路面下，系統趨向失穩的前輪轉角閾值較小。該結論也符合實際現象和理論邏輯。

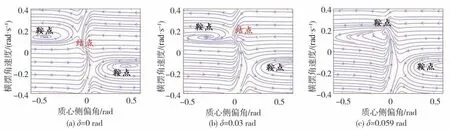
圖4 工況3相平面圖

3 穩定性分析結果仿真驗證

為驗證前述基于解析法的系統穩定性分析結果的可靠性，進一步開展整車動力學模型仿真。選取轉向盤角階躍輸入工況作為試驗工況，利用Matlab∕Simulink仿真平臺建立包括輪胎模型、空氣懸架模型的整車動力學模型，設置Simulink Parameters和終止時間，采用算法類型為變步長，算法為ode45的求解器對模型進行仿真。以橫向載荷轉移率（LTR）和橫向加速度為指標，分析系統穩定性。一般認為橫向載荷轉移率達到1.0，橫向加速度達到0.5g時，車輛將極易發生側翻，即系統失穩。為節約篇幅，這里僅選取高附路面車速為72 km∕h的工況1和低附路面車速為50 km∕h的工況3，進行分岔分析結果的仿真驗證。兩種工況下的客車橫向載荷轉移率（LTR）和橫向加速度仿真結果如圖6和圖7所示。

由圖6和圖7可見，當工況1前輪轉角達到0.096 rad，工況3前輪轉角達到0.057 rad，車輛的橫向載荷轉移率已達到1.0，而橫向加速度也超過0.5g，說明車輛處于臨界失穩狀態。此外在工況2和工況4的仿真結果中當臨界轉角分別為0.053和0.034 rad時車輛也同樣處于臨界失穩狀態，此時若受到微小干擾將極易發生側翻。考慮到輪胎模型的精度、模型迭算以及系統工作于強非線性區域，仿真結果與解析結果相比雖有些許不同（表2），但誤差較小能夠接受，可認為仿真分析結果與解析分析結果一致，證明本文提出的非線性穩定性分析方法的有效可行。

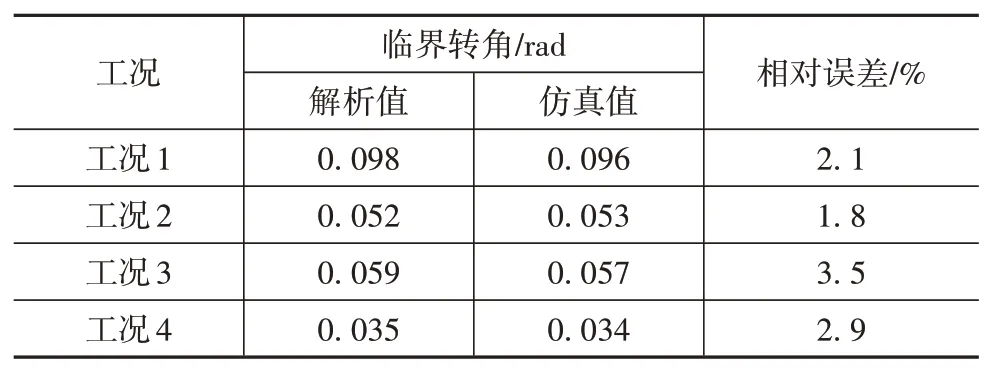
表2 臨界轉角值對比

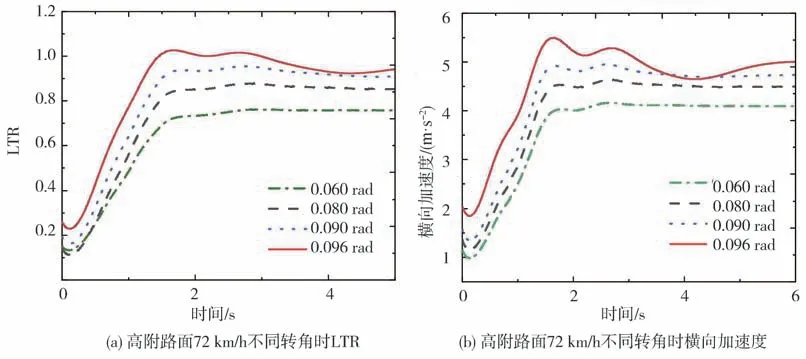
圖6 工況1 LTR和橫向加速度仿真結果

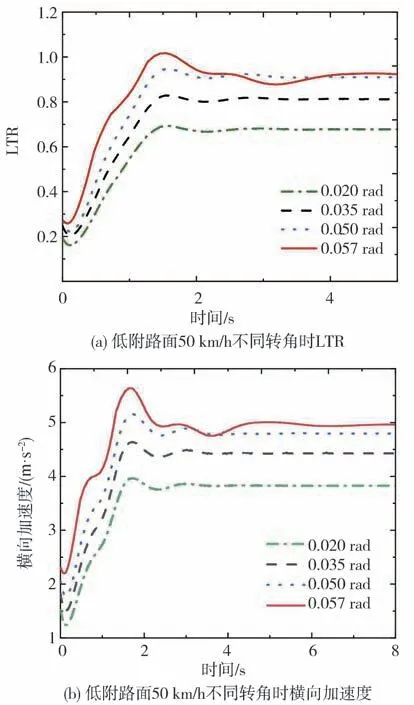
圖7 工況3 LTR和橫向加速度仿真結果

4 結論

本文中提出了一種系統非線性動力學建模方法，考慮了空氣彈簧和輪胎的非線性動力學特性。對高維復雜的系統降維得到了等價的約化系統，判斷出系統將會發生鞍結分岔。應用非線性動力學系統，通過對4種不同工況下系統在平衡點的分岔行為進行相平面分析，得到在不同路面條件下空氣懸架客車隨車速和前輪轉角變化的橫向動力學失穩規律。

基于整車動力學仿真對穩定性分析結果進行驗證，結果表明本研究能為提高客車橫向行駛安全和穩定性控制系統的設計提供依據。針對其他影響車輛穩定性的因素如整車結構參數的變化、更加復雜的路面條件等進行展開分析，采用更加精確的穩定性評價指標和多樣性的仿真工況將是后續研究的重點。