基于行駛數據挖掘的DCT車輛平直道路換擋規律研究*

秦大同，王 康，馮繼豪，劉永剛

（重慶大學，機械傳動國家重點實驗室，重慶 400044）

前言

換擋策略對車輛動力性和經濟性等性能的影響較大［1］，目前國內外學者對自動變速車輛的換擋策略進行了深入研究，主要分為兩類：基于車輛動力學制定換擋規律和基于智能算法訓練擋位決策模型。基于車輛動力學制定換擋規律，一般通過建立目標車輛動力學模型，在動力性等約束條件下，利用解析法等求取換擋規律，但該方法對不同行駛工況和駕駛風格的適應性差。文獻［2］和文獻［3］中通過優化特定工況下的換擋規律來提升其適應性。其中Song等［2］通過識別上下坡工況并修正該工況下的換擋規律，使車輛對該工況有較好的適應性。文獻［4］和文獻［5］中通過動態規劃算法在給定約束下求取已知工況的最佳換擋規律。但該類方法在實車應用過程中，為提升車輛綜合性能還須耗費大量人力物力在各類工況下做人工標定，且制定完成的換擋規律很難再更新。

基于智能算法訓練擋位決策模型，一般通過考慮駕駛風格、駕駛意圖和行駛工況的影響，利用支持向量機等智能算法學習熟練駕駛員的換擋策略，再通過訓練好的模型控制變速器換擋。張元俠［1］通過多維數據識別行駛工況，再利用支持向量機訓練擋位決策模型，并驗證該擋位決策模型的合理性。陳清洪等［6］利用動態模糊神經網絡擬合駕駛員換擋點進而控制換擋。該類方法可較好學習熟練駕駛員的換擋策略，適應性也較強，是擋位決策智能化的一個重要發展方向。但該類方法使用的智能算法計算量大，須裝備高性能計算芯片，目前無法大量應用于實車。

鑒于上述研究的不足，本文中結合兩類方法的長處，提出了一種通過挖掘海量行駛數據制定換擋規律的方法。首先，設計試驗采集熟練駕駛員駕車行駛數據，再通過數據的清洗、集成與特征拓展和平直道路數據的篩選、特征提取、離群點去除與數據標準化來提取影響平直道路換擋策略的3個最主要特征的標準化數據，然后通過對各擋位下決策值分類精度最高的隨機森林算法生成三參數換擋規律。通過挖掘熟練駕駛員在平直道路上駕車行駛數據中的換擋策略來制定換擋規律，可將熟練駕駛員對車況和道路工況等的綜合考量融入換擋規律中，并增強其工況適應性，避免了復雜的人-車-路建模和人工標定過程，縮減了開發周期；通過將訓練過的擋位決策模型轉換為換擋規律，使該方法可直接應用于實際車輛。

1 數據采集

為使數據挖掘結果更具實用性，設計了實車道路數據采集試驗。為避免不同駕駛風格對換擋策略挖掘的影響，按文獻［7］中的方法，選擇20位駕駛風格為“標準型”的熟練駕駛員進行數據采集試驗，其駕齡都超過2年，平均駕齡為8.6年。假設數據采集試驗中熟練駕駛員的換擋策略為最佳換擋策略，不對其換擋策略根據最佳經濟性等指標進行篩選或修正。

試驗車為某型裝備7擋DCT變速器的SUV，通過車輛OBD接口和Vehicle Recorder數據采集設備讀取行駛數據，如圖1所示。

圖1 試驗車輛與數據采集設備

為保證采集數據更全面和更接近實際行駛環境，在重慶市公路交通網中選取了一段包含市區道路、城郊道路、山路和快速路的行駛路線，路線總長約為100 km，如圖2所示。

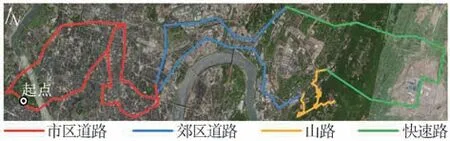
圖2 數據采集試驗行駛路線

在確認駕駛員適應試驗車操作特性后，開始試驗，最終共采集109.88 h行駛數據。采集數據包括實際擋位、目標擋位、轉向盤轉角、車速、縱向加速度、制動油壓、節氣門開度、加速踏板位置、發動機轉速和發動機轉矩等。因為采集的數據來源于多個傳感器，其時序信息不一致，且部分數據存在噪聲和缺失值，故須進行數據預處理，以便后續對換擋規律的挖掘。

2 數據預處理

圖3為本文挖掘的平直道路下熟練駕駛員換擋策略方法的整體結構框圖。數據預處理部分主要包括數據清洗與集成、特征拓展與數據篩選、主要特征提取、離群點去除和數據標準化。

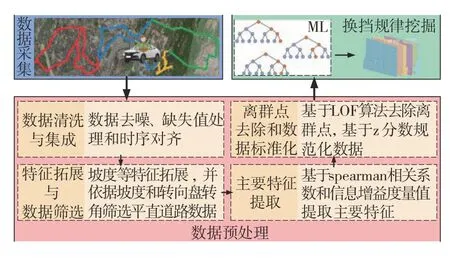
圖3 換擋規律挖掘方法結構框圖

2.1 數據清洗與集成

由于CAN通信偶發性丟包等因素會導致部分數據缺失，故須進行缺失值處理。經檢測發現縱向加速度數據存在少量缺失值，且系統用“-16”表示該缺失值，如圖4（a）所示。缺失值的處理方法可分為刪除和填充兩類。縱向加速度數據中缺失值一般單個出現，若直接刪除會影響后續數據處理，因此本文通過區域中心度量來填充該缺失值，處理結果見圖4（b）。

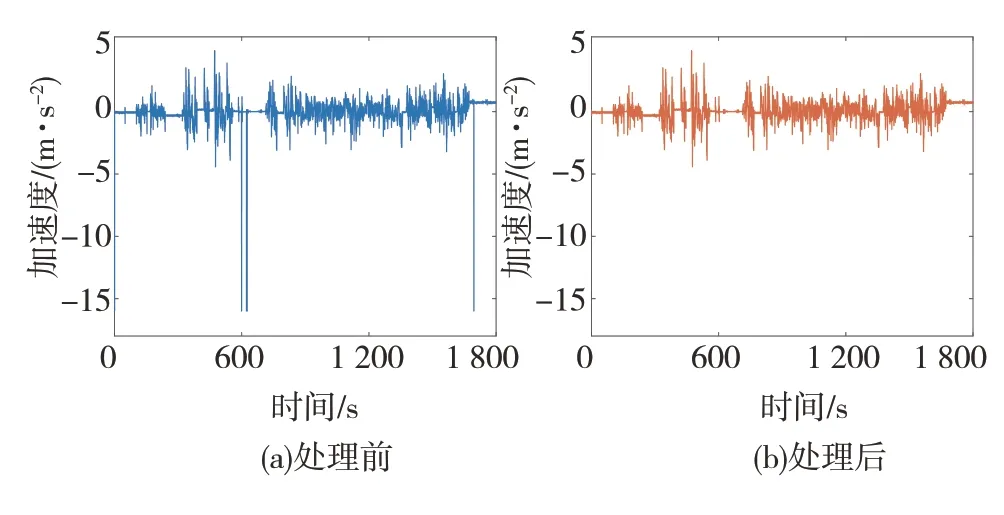
圖4 異常值處理

車身振動等因素會導致采集數據包含噪聲，本文采集數據中存在噪聲的數據有：車速、縱向加速度、制動油壓和發動機轉矩。因為存在噪聲的特征占比較大，如不進行去噪處理，將會嚴重影響數據挖掘效果。為此，利用去噪效果較好的小波去噪算法對4個含噪聲特征進行去噪處理，閾值函數選擇硬閾值。因為4個特征的頻譜特性不同，故針對該4個特征采用的小波基函數分別為：sym3、haar、sym3、db6，分解層數分別為4、3、4、4，處理結果見圖5。

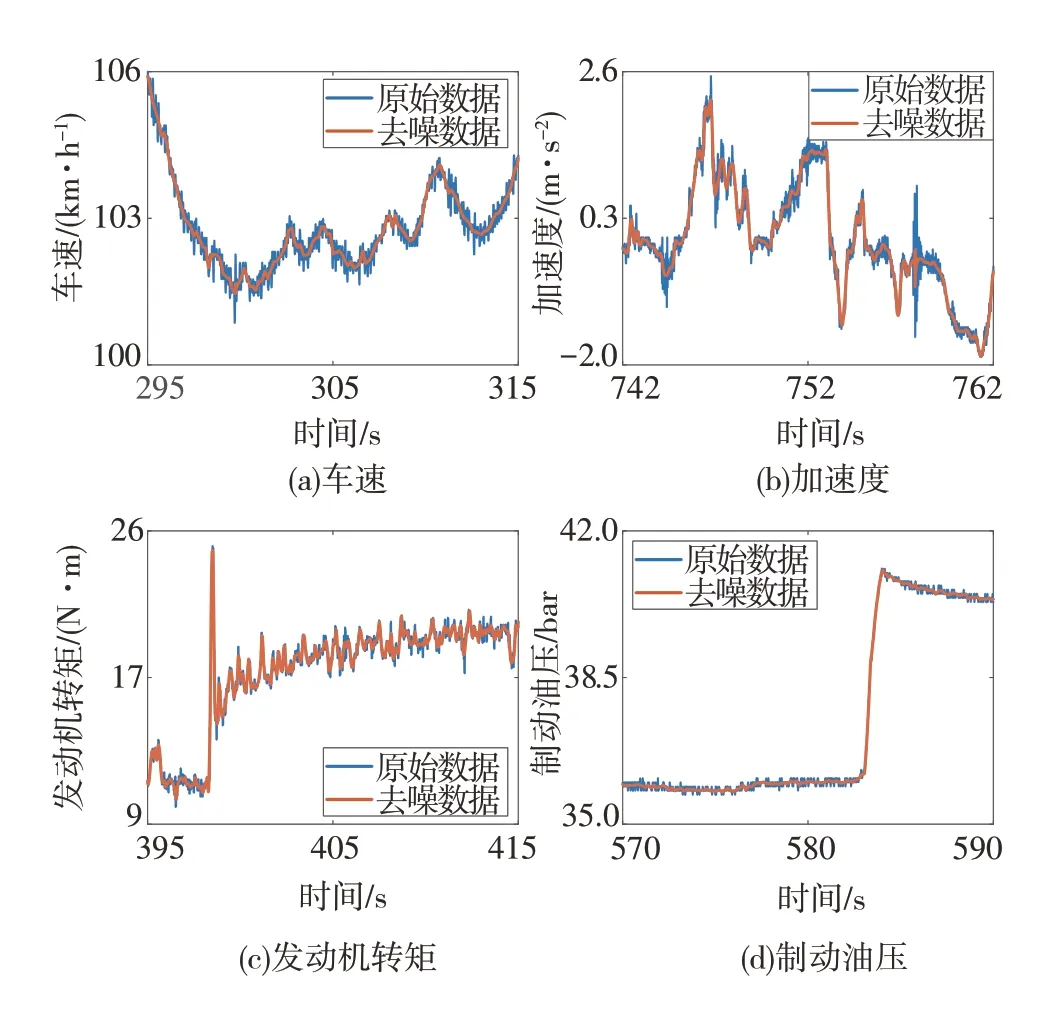
圖5 去噪處理結果

表1為各特征采樣頻率和采樣精度。由表可知，由于涉及多個傳感器，各特征的采樣頻率和時序信息不統一。如果時序信息不能保證一致，則無法同時分析多個特征，數據挖掘效果也會變差，因此須進行頻率統一和時序對齊處理。該處理一般采用插值的方法，為保證處理后的數據不失真，本文采用樣條插值算法，并以車速的采樣頻率和時序信息作為基準。

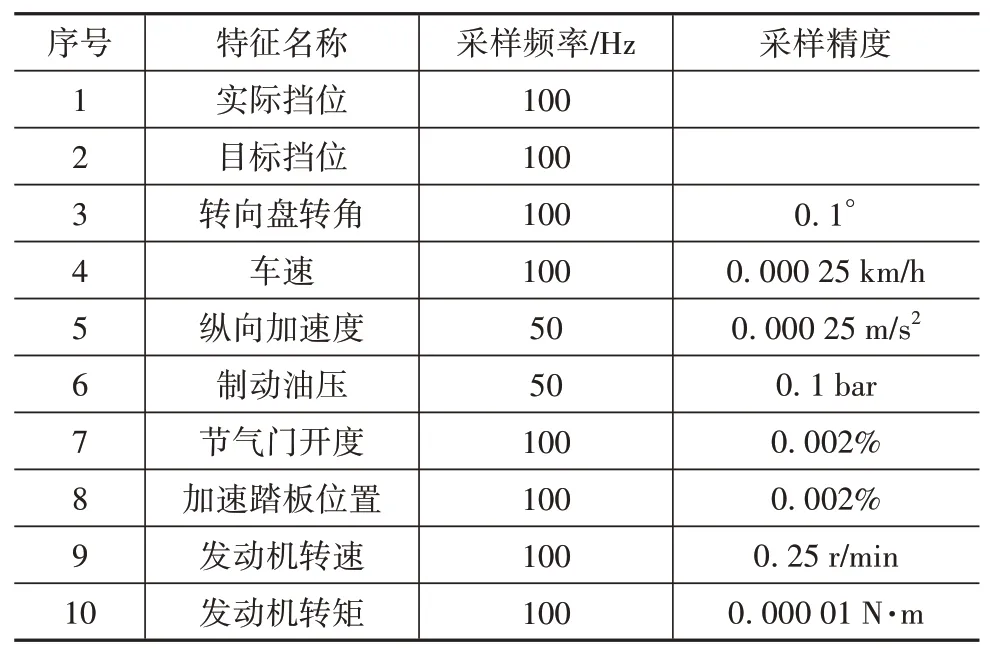
表1 各特征采樣頻率和采樣精度

2.2 特征拓展與數據篩選

通過車載傳感器采集的數據還不夠全面，可能遺漏對于換擋規律挖掘非常重要的信息，例如挖掘平直道路換擋規律還需要道路坡度數據。因此須通過已有數據拓展出較為全面的特征組合。本文根據文獻［8］中提出的方法，由實際擋位、車速、縱向加速度、發動機轉矩和實車參數估計道路坡度（road slope，RS；序號：11），再由部分特征對時間求導來拓展特征，如表2和圖6所示。

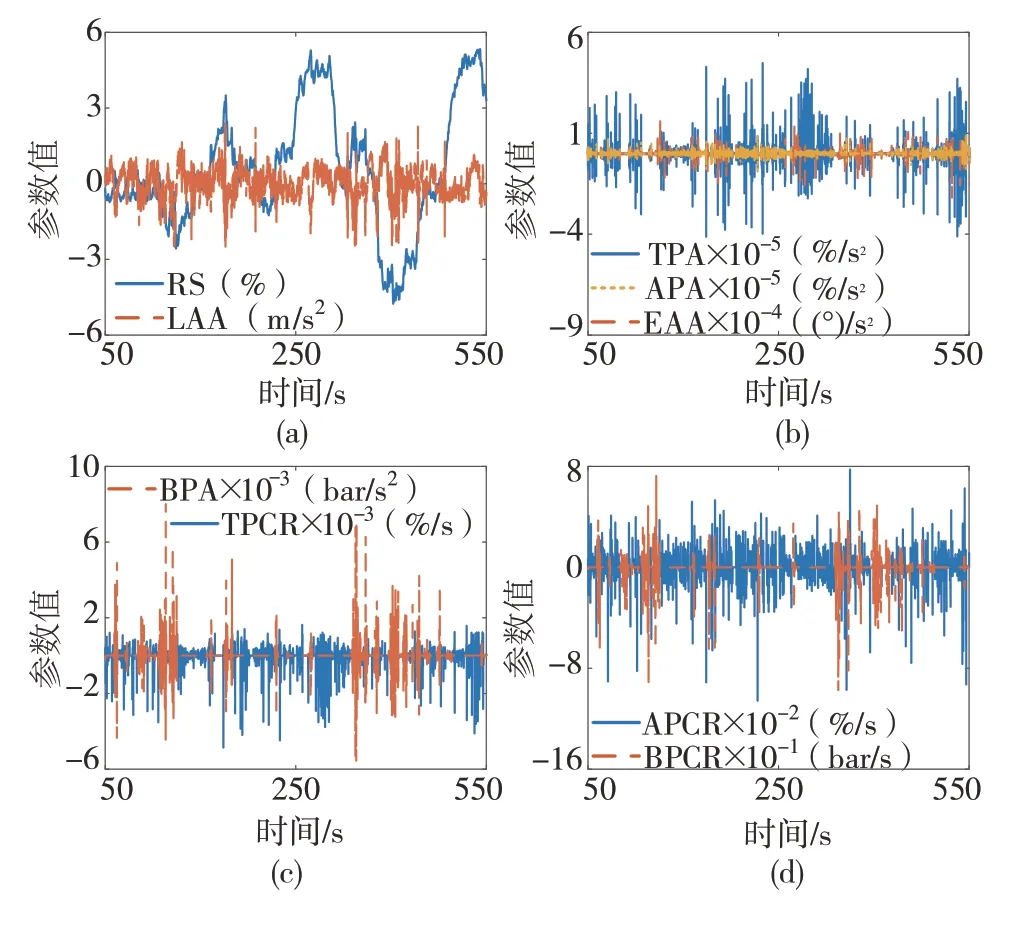
圖6 拓展特征部分展示

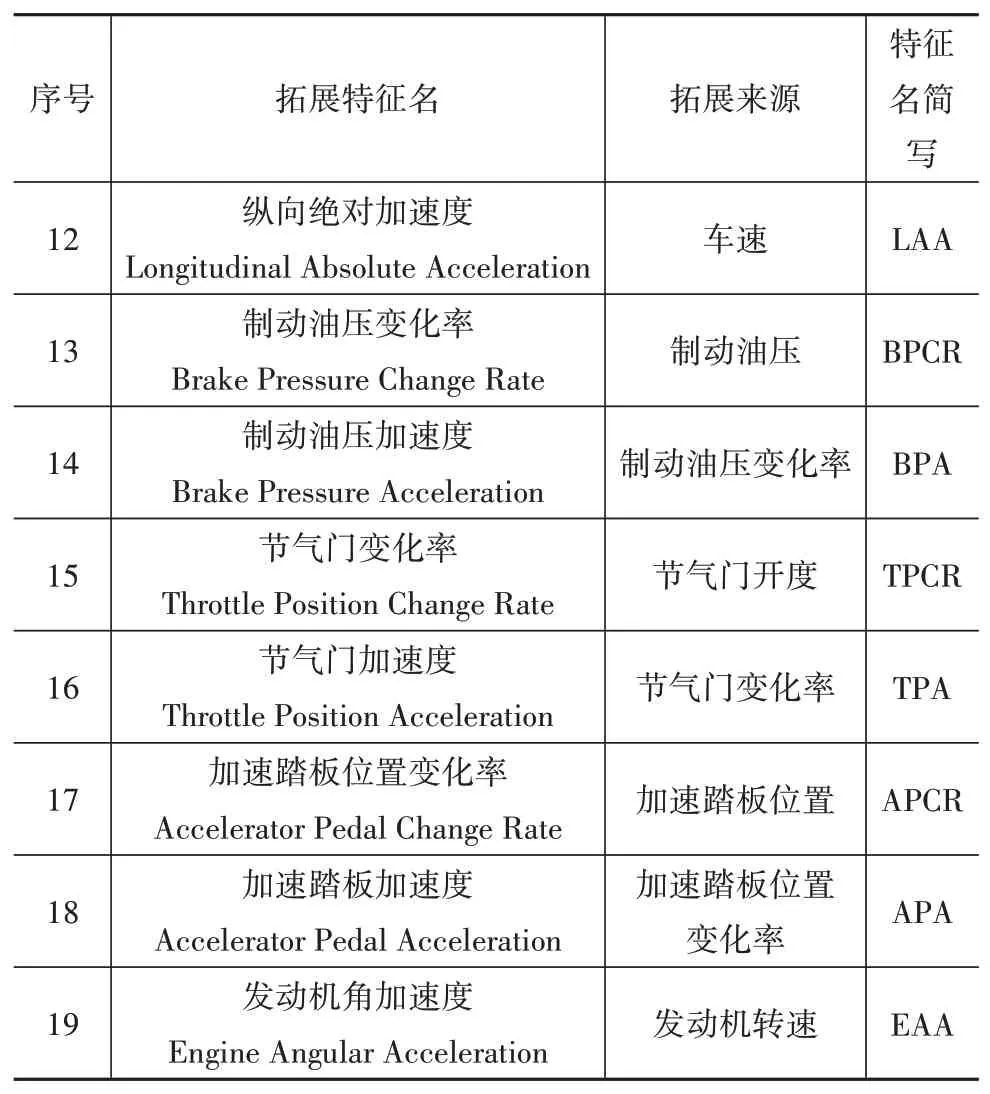
表2 特征拓展

文中所述平直道路工況是指車輛水平直線行駛工況，且試驗車廠商提供的參數中轉向盤自由行程為18°，同時試驗車在水平地面行駛時，估計的坡度值在±2%范圍內波動，此外停車工況無關擋位決策。因此提取車速大于0，且轉向盤轉角在±18°范圍內，同時坡度在±2%范圍內的數據點作為平直道路工況的數據點。

2.3 主要特征提取

本文最終目標是提取三參數換擋曲面，因此須提取影響換擋策略的3個最主要特征，為避免冗余特征干擾，在特征重要性分析前須去除冗余特征［9］。上述19個特征中，實際擋位和目標擋位屬于標簽特征，轉向盤轉角和坡度屬于篩選特征，縱向加速度是車載加速度計測得的不包含重力加速度分量的相對加速度，且已由車速拓展成縱向絕對加速度，所以先去除該5個特征。為進一步去除冗余特征，還須分析剩余14個特征的相關性。經Kolmogorov-Smirnov檢驗，14個特征都不符合正態分布，故通過spearman相關系數分析14個特征彼此間的相關性，結果見表3。表3中車速、制動油壓、節氣門開度、加速踏板位置、發動機轉速和發動機轉矩的特征名分別簡寫為VS（vehicle speed）、BP（brake pressure）、TP（throttle position）、APP（accelerator pedal position）、ES（engine speed）和ET（engine torque）。

spearman相關系數絕對值大于0.6表明特征間有強關聯性［10］。為得到關聯性最小的特征組合，對比表3中相關系數值，將節氣門開度、發動機轉速、發動機轉矩和縱向絕對加速度去除。冗余特征去除后，剩余10個特征，為篩選出3個最主要特征，還須進行特征重要性分析。

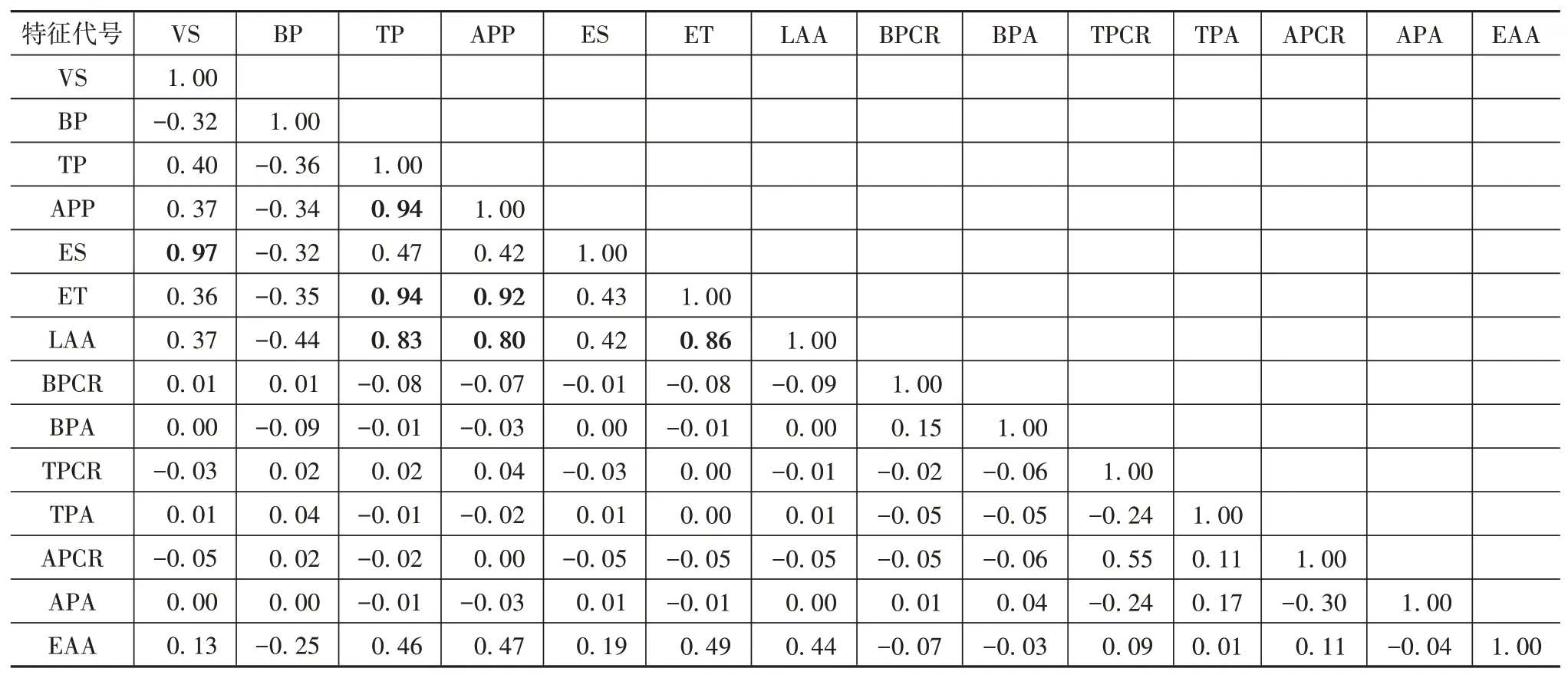
表3 特征間spearman相關系數

文中將換擋規律挖掘轉換為每個擋位下的升降擋和保持的分類問題，降低了分類難度，有效提高了分類精度，但也須為每個擋位建立一個分類模型，以對每個擋位分別進行特征重要性分析。通過可評價分類效果的信息增益度量來衡量各特征的重要性：

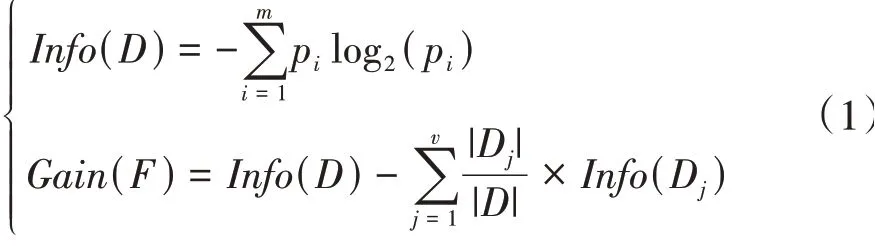
式中：D表示某一分組；m為類的總數；pi為D中任一數據屬于i類的非零概率；F表示某一特征；v表示D子分組的個數。結果見表4。

表4中各擋位下車速、加速踏板位置、發動機角加速度3個特征的重要性都排前三，且重要性之和最低為0.831。為降低換擋規律的復雜度和增強其實用性，將車速、加速踏板位置和發動機角加速度作為各擋位分類模型的辨識特征。

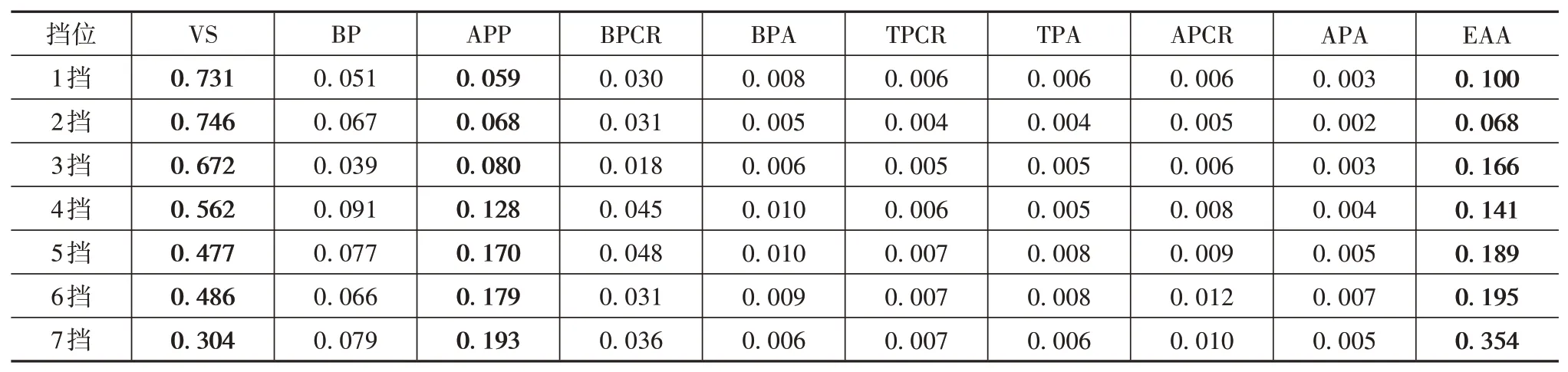
表4 各擋位下特征信息增益度量值

2.4 離群點去除與數據標準化

因為須對每個擋位下的升擋點、保持點和降擋點進行分類，但每個擋位數據中都存在離群點，而離群點的存在會影響分類精度，故須進行離群點去除。選擇基于密度且不受數據分布影響的Local Outlier Factor算法對每個擋位的離群點進行檢測和去除［11］，各擋位下升擋點、保持點、降擋點和離群點分布見圖7。

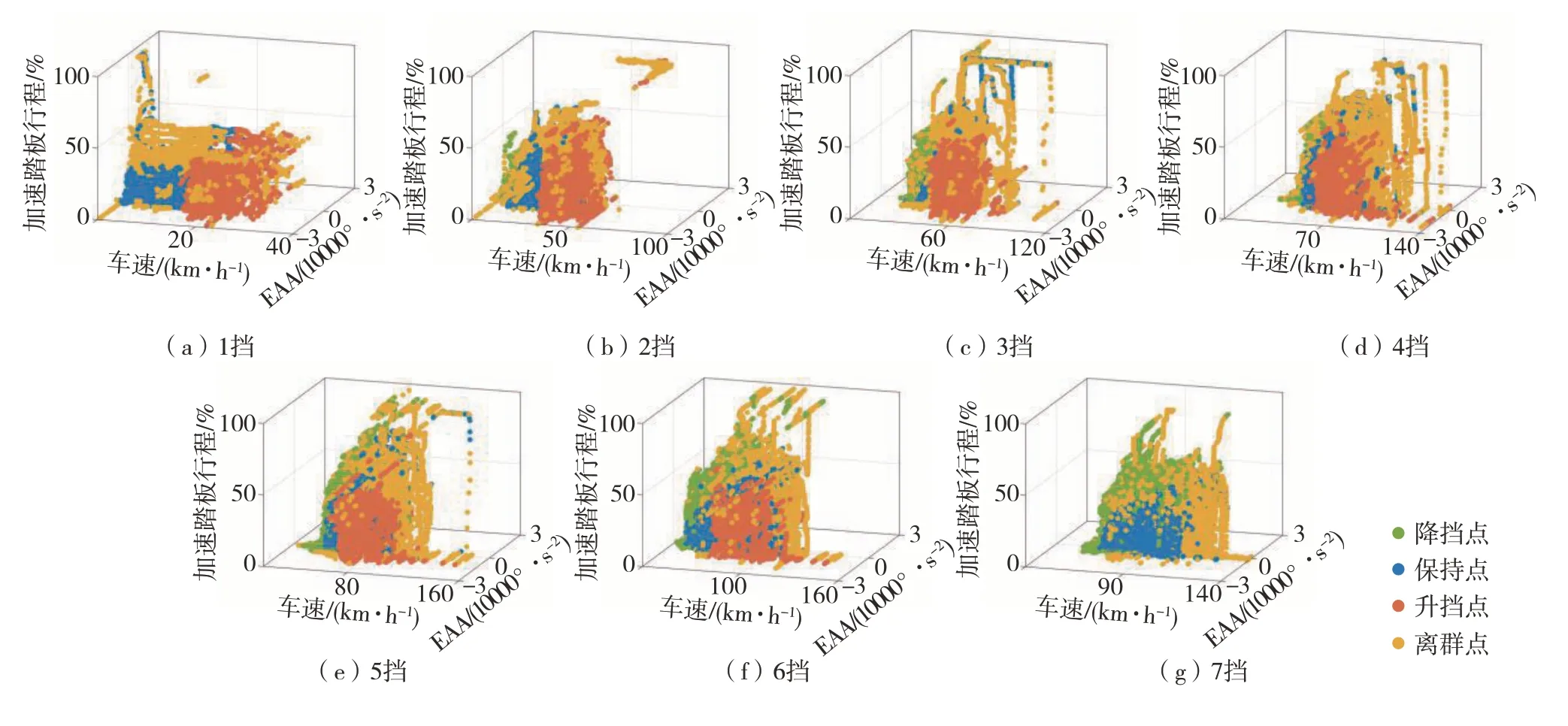
圖7 各擋位下升擋點、降擋點、保持點和離群點分布

此外，由于最終選取的3個重要特征的量綱不同，為避免其對分類算法精度的影響，采用魯棒性較好的均值絕對差z分數方法對各擋位數據進行標準化處理，其計算公式為

式中：x'i為標準化處理后的數據；xi為原始數據為x的均值；sA為均值絕對偏差。

數據預處理后，最終得到的各擋位數據點個數分別為350 958、812 092、942 934、856 130、889 210、942 720、1 067 440。其中1擋數據點明顯少于其它擋位，經分析是因為轉彎和爬坡一般在低擋位，而本文挖掘的是平直道路換擋規律，因此通過數據篩選，1擋的數據點較少。此外，行駛路線中有較多高速路或快速路，同時該工況下彎道和坡道較少，因此處理后的數據中高擋位數據較多。

3 換擋規律挖掘

在經過數據預處理得到的各擋位數據中，1擋數據有升擋和保持兩類，7擋數據有保持和降擋兩類，其余5擋數據有升擋、保持和降擋3類。因此須對7組數據分別訓練分類模型，目前有監督學習中分類效果較好的算法：C4.5、邏輯回歸、K最近鄰、樸素貝葉斯、支持向量機和隨機森林等［12］。其中C4.5算法易過擬合，邏輯回歸算法和K最近鄰算法在處理數據不平衡問題上效果較差。而本文處理的分類問題要求分類算法不能過擬合，否則會導致分類模型外延性差，且影響后續升降擋曲面的生成，同時原始數據集中升擋點和降擋點數量相對保持點較少，所以分類算法須克服數據不平衡問題［13］。因此本文采用樸素貝葉斯（naive Bayes，NB）、支持向量機（support vector machine，SVM）和隨機森林（random forest，RF）3種分類算法分別對7組數據進行分類，其中SVM采用4種核函數，分別為linear核函數、polynomial核 函 數、RBF核函數和sigmoid核 函 數。之后通過10-折交叉驗證的平均準確率比較各算法的分類精度，并篩選出效果最好的分類算法用于各擋位數據點的分類。各算法對決策值的分類精度見表5。

3.1 換擋策略學習

分類算法精度對比見表5。由表可知，6種分類算法在4擋、5擋和6擋的分類精度都稍低于其它擋位。對比表4可以發現，這是因為3個重要特征在4擋、5擋和6擋的重要性之和低于其它擋位，也即3個重要特征在4擋、5擋和6擋中對升擋、保持和降擋的區分能力稍弱。

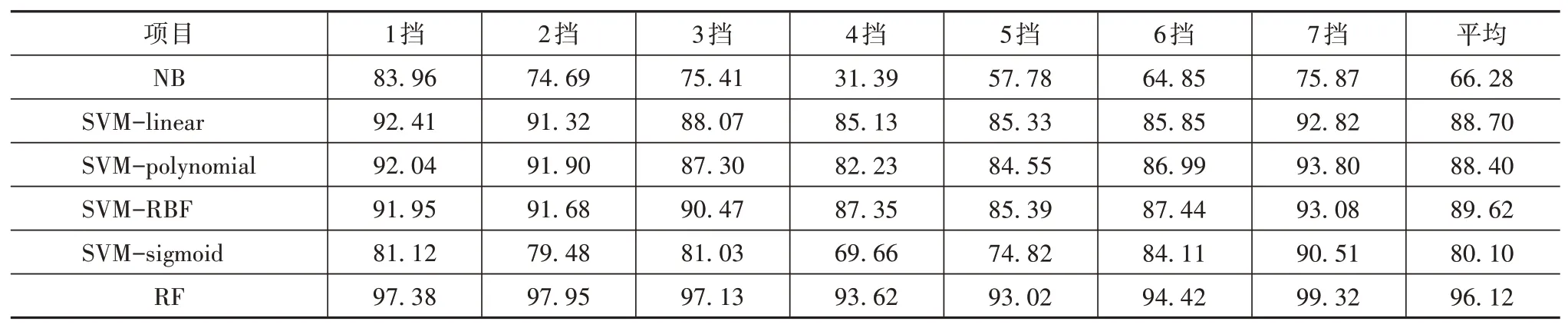
表5 分類算法精度對比 %

對比6種分類算法，其中NB的分類精度最差，RF最高，且RF在所有擋位的分類精度都超過了93%，平均分類精度更是達到了96.12%。圖8為各擋位下RF混淆矩陣。在圖8中，每個擋位下，“保持”的識別率最高，這是因為“保持”類數據點的占比很大，導致算法在追求總分類精度時犧牲了小類的識別率，但每個擋位的升擋和降擋識別率最低也達到83.50%，且大部分超過90%，與“保持”類識別率相近，這表明RF具有很強的抗數據不平衡能力，可以很好處理本文中的分類問題，因此采用RF對7個擋位分別建立分類模型。

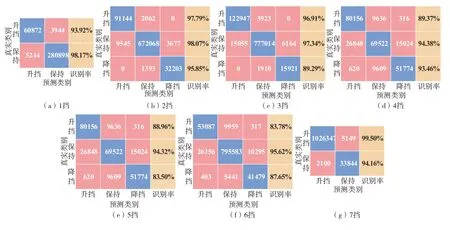
圖8 各擋位下RF混淆矩陣

3.2 換擋規律提取

在提取換擋曲面時，先對由車速、加速踏板位置和發動機角加速度構成的三維空間按離散精度生成待分類點集，并通過訓練好的分類模型對所有離散點進行分類，再分別提取升降擋點群的邊界點生成換擋曲面。表4中各擋位下車速都很重要，因此將車速特征作為主特征，用另兩個特征構成換擋曲面。因為升擋是從低速到高速，降擋是從高速到低速，所以將分類后的升擋點群在車速維度（車速值左小右大）的最左曲面作為升擋曲面，將降擋點群在車速維度的最右曲面作為降擋曲面。

根據圖7中數據點分布情況，設置待分類空間中車速、加速踏板位置和發動機角加速度取值范圍分別為0～160 km∕h、0～100%和-30 000°∕s2～30 000°∕s2。由發動機轉速采樣精度和采樣時間得發動機角加速度精度為150°∕s2，而車速和加速踏板行程的精度分別為0.000 25 km∕h和0.002%，在考慮計算成本后，設置各特征離散精度分別為0.01 km∕h、0.01%和150°∕s2，則待分類點共有6.4×1010個，換擋曲面共有4×106個數據點。此外，在對各擋位數據點分類前要根據式（2）標準化數據，并在分類后將數據還原，最終提取的換擋規律見圖9。

圖9中換擋曲面并不光滑，這表明局部最優點被保留，且升降擋曲面都有隨著加速踏板行程變大，對應車速變大的趨勢，這與動力性換擋規律相似。此外，換擋曲面有交叉情況，但本文挖掘的是各擋位下升降擋換擋規律，生成的換擋規律也需逐級判斷升降擋，因此換擋曲面交叉不影響擋位決策。

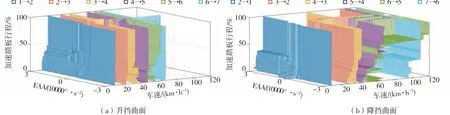
圖9 數據挖掘換擋規律

4 仿真驗證

為驗證所挖掘換擋規律的實用性，同時考慮試驗安全性，在Simulink環境中搭建模型并進行仿真驗證。該仿真模型由駕駛員模型、車輛動力學模型和道路模型組成，其中駕駛員模型以PID控制為基礎建立，車輛動力學模型由發動機模型、變速器模型和行駛阻力模型組成，道路模型由道路坡度和循環工況組成。其中車輛動力學模型中的各項參數采用試驗車參數，如表6所示。

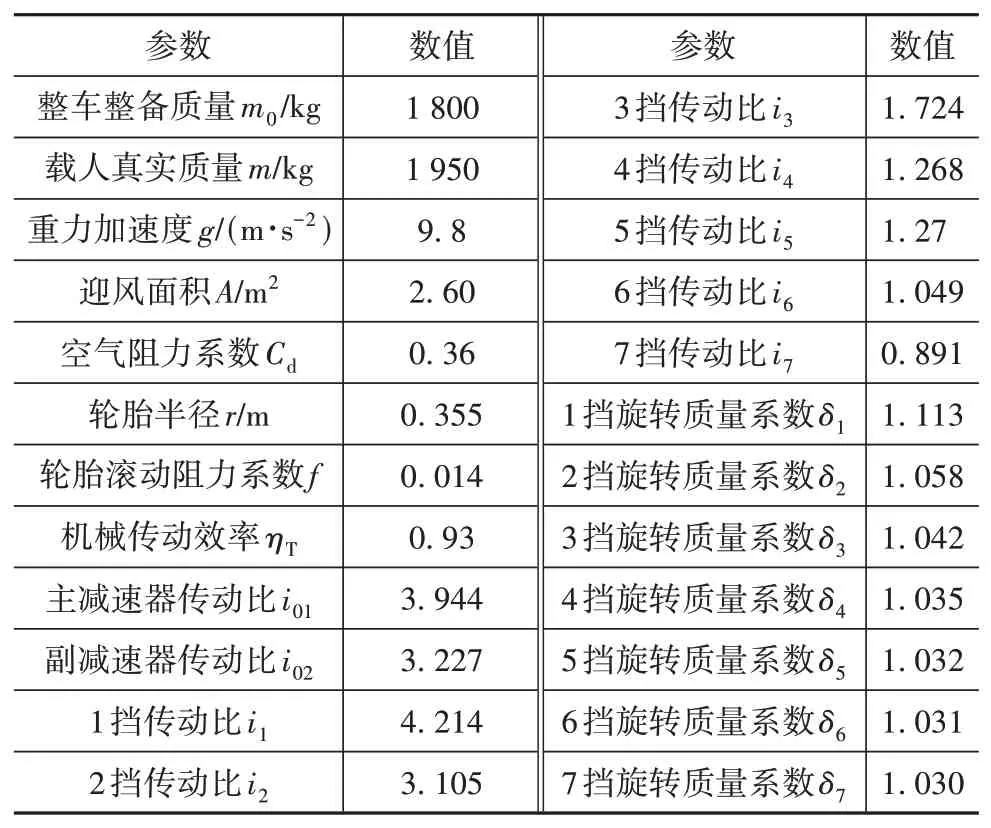
表6 實車參數

仿真驗證中，通過文獻［14］中的方法制定經濟性換擋規律和動力性換擋規律，并與本文所挖掘的換擋規律作對比。仿真驗證包含兩個部分，第一部分是百公里加速仿真，主要對比動力性，第二部分是CLTC-P循環工況仿真，主要對比經濟性和換擋次數。采用的CLTC-P循環工況為中國乘用車行駛工況，其累計里程為14 480 m，更接近國內乘用車駕駛實際情況，且包含數據采集試驗中的城市工況、郊區工況和高速工況（分別對應圖12中0-674、675-1 367和1 368-1 800 s工況），可全面檢驗所挖掘換擋規律的實用性。

此外，發動機角加速度很少出現絕對值大于30 000°∕s2的情況，且圖9中的每個換擋曲面上，當發動機角加速度絕對值大于25 000°∕s2時，每一加速踏板位置下車速值基本不變，因此仿真中當發動機角加速度絕對值超過30 000°∕s2時，默認其絕對值為30 000°∕s2。

4.1 百公里加速仿真

百公里加速仿真中，駕駛員模型的加速踏板行程設置為100%，制動壓力設置為0，轉向盤轉角設置為0，道路模型中道路坡度設置為0，不設置循環工況，仿真結果如圖10和圖11所示。

圖10中數據挖掘換擋和經濟性換擋的加速時間較動力性換擋分別超出17.52%和45.71%。且經濟性換擋的換擋節奏最快，車速到100 km∕h時，其擋位為7擋，而數據挖掘換擋為4擋，動力性換擋為3擋，這也導致其動力性一直弱于其它兩種換擋規律。此外，數據挖掘換擋的換擋趨勢介于經濟性換擋和動力性換擋之間，雖加速時間比動力性換擋多1.51 s，但其動力性較經濟性換擋有明顯提升。圖11中因升擋時變速器傳動比降低，發動機轉速下降，導致換擋時發動機角加速度先下降后升高。

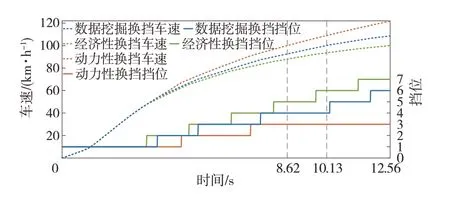
圖10 百公里加速仿真結果

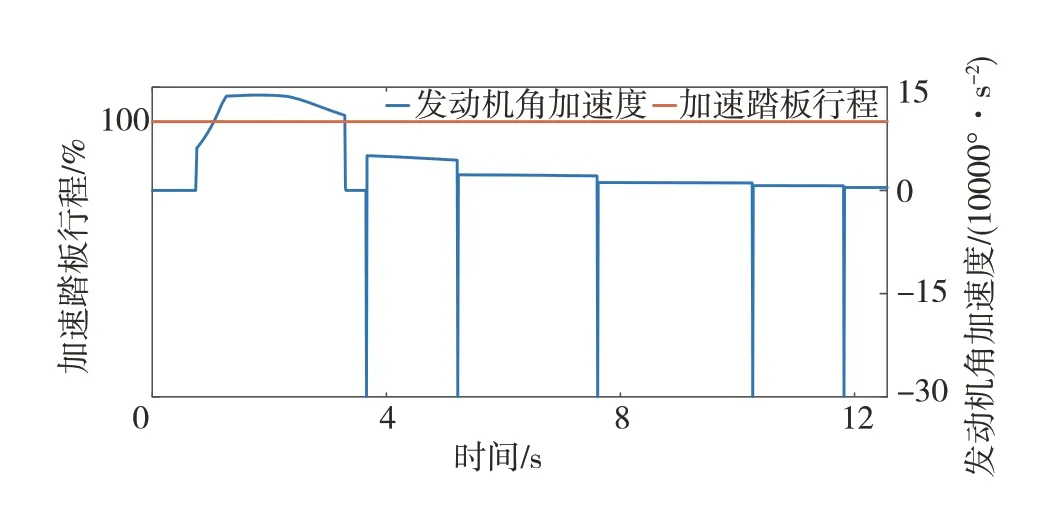
圖11 百公里加速仿真中數據挖掘換擋相關參數

4.2 CLTC-P循環工況仿真

CLTC-P循環工況仿真中，駕駛員模型的轉向盤轉角設置為0，道路模型中道路坡度設置為0，循環工況設置為CLTC-P，仿真結果如表7、圖12和圖13所示。

表7表明，數據挖掘換擋油耗接近經濟性換擋，且動力性換擋油耗較大。圖12中經濟性換擋節奏同樣很快，而動力性換擋節奏較遲緩，表7中換擋次數數據也體現了這一點。同時，經濟性換擋為追求經濟性經常出現低速高擋位的情況，雖有效降低了油耗，但換擋次數較另兩種換擋規律猛增。不過經濟性換擋在高速工況中能跟隨車速的變化及時換擋，更適應該工況，而動力性換擋更適應城市工況，其換擋次數少，在城市工況中可避免頻繁換擋，但在另兩個工況中則會出現延遲升擋的情況，相比于動力性∕經濟性換擋，數據挖掘換擋則始終能根據車速變化情況及時調整擋位，對城市工況、郊區工況和高速工況都有較強的適應性。動力性換擋雖在換擋次數方面表現較好，但這只是其延遲升擋帶來的好處，而缺點則是平均油耗較經濟性換擋增加了20.66%。與經濟性換擋相比，數據挖掘換擋規律，在平均油耗微增0.89%情況下，換擋次數大幅減少了63.33%，在保證較強經濟性的同時也減少了變速器的磨損。

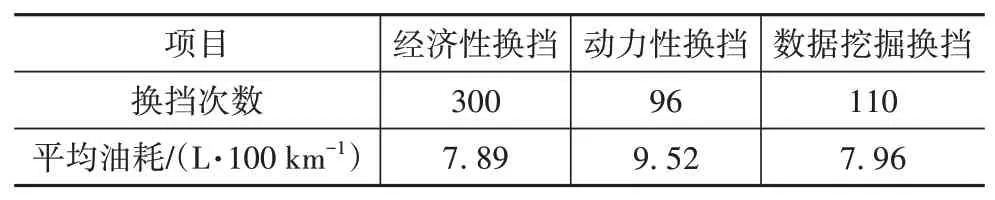
表7 換擋次數和平均油耗

由圖12和圖13可見，數據挖掘換擋規律具有較強的實用性，即更接近經濟性換擋規律，經濟性較好，但其動力性比經濟性換擋也有較大提升，較動力性換擋也未大幅下降。總的來說，數據挖掘換擋規律在保持較低油耗的同時，顯著提高了車輛動力性，減少了換擋次數，在經濟性和動力性間有較好平衡，綜合性能較好，這驗證了本文所提方法對熟練駕駛員換擋策略的有效挖掘，也驗證了所挖掘換擋規律的實用性。

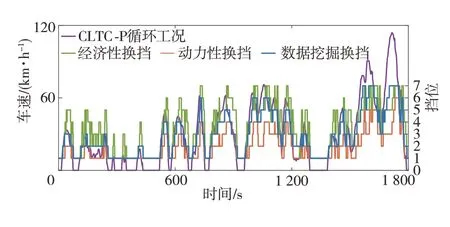
圖12 CLTC-P循環工況仿真結果

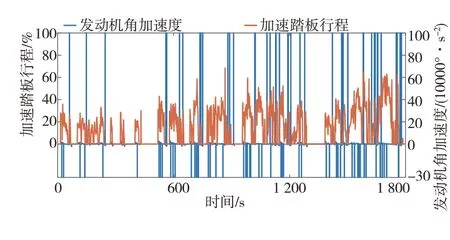
圖13 CLTC-P循環工況仿真中數據挖掘換擋相關參數

此外，經在CPU為i5-9400F∕2.9 GHz、內存為16 G∕2400 MHz的計算機上測試，由隨機森林算法訓練的擋位決策模型預測一次擋位的平均用時為1.38×10-4ms，而由三參數換擋規律查詢一次擋位的平均用時為3.8×10-5ms，下降了72.46%，明顯降低了計算量。且現有變速器控制芯片的計算性能遠不如上述計算機，因此基于智能算法的擋位決策模型無法廣泛用于現有實車。而由本文方法制定的三參數換擋規律數表不需要高性能芯片，可通過替換現有變速器換擋規律數表直接應用于實車，普適性更好。

5 結論

針對目前自動變速車輛擋位決策方法對環境適應性差或難以直接應用于實車的問題，本文通過挖掘熟練駕駛員駕車行駛數據來提取平直道路三參數換擋規律。首先通過數據預處理從試驗采集數據中提取出平直道路工況下3個最重要特征（車速、加速踏板位置和發動機角加速度）的標準化數據，然后比較6種機器學習算法對各擋位下3種決策值的分類效果，選用效果最好的隨機森林算法提取各擋位下換擋規律。仿真結果表明，該方法普適性好，能有效提取熟練駕駛員換擋策略，提取的換擋規律適應性較好，在保證較好經濟性的同時，也具有較好的動力性，且換擋次數較少，綜合性能好。