魯班鎖的別樣玩法

邵勇

在沒有釘子、繩子的情況下，你能將6根木條交叉固定在一起嗎？木匠祖師魯班就發(fā)明了一種方法，用咬合的方式把3組木條垂直相交固定。6根木條中間有缺，缺缺相合。這種三維的拼插器具在建筑上也被廣泛應(yīng)用，是中國古代傳統(tǒng)的土木建筑固定結(jié)合器。

三國時期，孔明把魯班的發(fā)明制成了一種玩具。這種玩具雖然看上去簡單，但是內(nèi)中奇妙無窮，不得要領(lǐng)很難完成拼合，是一種老少皆宜的休閑玩具。

魯班鎖亦稱孔明鎖、別悶棍等。從外觀上看，它是嚴絲合縫的十字立方體，動動腦筋即可拆解。但要重新拼裝好可不是那么容易的，拼裝時需要仔細觀察，認真思考，分析其內(nèi)部結(jié)構(gòu)。除了能對魯班鎖進行拼裝、拆解外，我們還可以從數(shù)學的角度來研究魯班鎖。

魯班鎖由6根方柱交叉拼接而成。因為6根方柱互有重合的地方，所以有些方柱肯定不是完整的，而是被挖掉了一部分。也正因為這樣，魯班鎖才會產(chǎn)生如此巧妙的拼裝方式。

從外面觀察拼裝好的魯班鎖，我們可以發(fā)現(xiàn)每根方柱之間沒有一絲空隙。但光用眼睛看還不夠，雙手也要動起來呀！一起來算出魯班鎖的體積吧。

計算拼裝好的魯班鎖的體積有很多種方法。今天主要介紹2種：一種是將魯班鎖分解成容易計算體積的幾個組成部分，另一種是運用能使重疊部分不被重復(fù)計算的容斥原理。

假設(shè)1根完整的方柱可以均分為4個小正方體，每個小正方體的體積看作單位1，1根完整的方柱的體積為4。

如圖1所示。魯班鎖表面露在外面的部分，可以分成2種不同的類型。第一種是圖中的藍色小正方體，體積為單位1。這樣的正方體上、下、左、右、前、后各2個，一共有12個。它們都位于魯班鎖的最外端，體積之和為12。第二種是圖中的綠色小長方體，它的體積為小正方體的1

4，位置在角落處。這樣的小長方體每根方柱上面有2個，一共有12個，體積之和為12×1

4=3。

接著，我們再計算沒有表面露在外面的部分的體積。這部分體積分成2種類型。一種是有“邊”露在外面的，如圖2所示，根據(jù)2條青色線段（有一條是MN），我們可以定位出這個被壓在里面的“半方塊”。這個“半方塊”的體積是小正方體的一半，它位于C、D方柱的上方，同時被擠壓在A和B之間，但它也是方柱E的一部分。這樣的“半方塊”有6個（兩兩相對），體積為6×1

2=3。另一種是只有4個頂點稍微露出來的最中間的單位正方體，它的體積為1。

因此，魯班鎖的總體積為：

12+3+3+1=19

它比原來6根完整方柱的總體積少了24-19=5（個）單位體積。

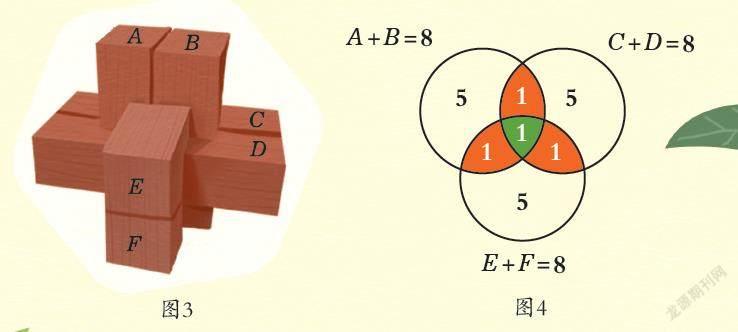
如圖3所示，A和B并排放到一起可以當成一個整體，C和D、E和F也可以當成一個整體。每個整體的體積都是8，分別對應(yīng)圖4文氏圖中的3個圓。每兩個整體的公共部分是2個單位正方體，這相當于文氏圖中的一個棗核形。魯班鎖正中間的完全隱藏起來的單位正方體，就相當于圖4中間的綠色曲邊三角形。魯班鎖的體積就是文氏圖中3個圓的并集。

為方便起見，我們設(shè)A+B=X，C+D=Y，E+F=Z，并且X=Y=

Z=8。下式中“∪”表示并集，“∩”表示交集。根據(jù)容斥原理，有：

（A+B）∪（C+D）∪（E+F）

=X∪Y∪Z

=X+Y+Z-X∩Y-Y∩Z-Z∩X+X∩Y∩Z

=8+8+8-2-2-2+1

=19

以上用2種方法求出了魯班鎖所占據(jù)空間的體積，都為19。

魯班鎖是一種涉及立體幾何知識的玩具。通過幾何分割，6根木條可以有多種鎖定方式，組成的樣式多達119 963種。古典玩具見證了中國古代的悠遠文明，也讓我們認識到數(shù)學就蘊藏在游戲之中。

你喜歡玩玩具嗎？有的時候，咱們還能一邊玩玩具，一邊學數(shù)學呢。不信？趕緊掃描二維碼，關(guān)注“廣西期刊傳媒集團”，和我們一起玩玩具，一起學數(shù)學吧。