矩形鋼管混凝土柱初始缺陷隨機有限元分析*

楊 磊，薛曉宏，姜繼果，黃正業，姜子麒

(中鐵二十局集團第六工程有限公司，陜西 西安 710032)

0 引言

隨著我國經濟的發展，城市化進程不斷加速，土地資源日趨緊缺，超高層、大跨度建筑開始受到青睞，由于鋼管混凝土具有承載力高、塑性和韌性好、施工方便、耐火性能好、經濟效益好、輕質化等優點[1-2]，且矩形鋼管混凝土柱變形能力強、截面慣性矩大、節點構造簡單及使用性強[3]，因此被廣泛應用于現代化建筑結構中。理想狀態下，鋼管和混凝土應緊密接觸，共同承受外部荷載；但實際施工過程中存在混凝土振搗不密實，鋼管內部有加勁肋、內隔板及后期混凝土養護不合理等因素的影響，不可避免地會導致核心混凝土內部產生缺陷[4-5]。

自1957年 Kloppel等[6]開始研究圓鋼管混凝土軸心受壓柱，并探討該類構件承載力的計算方法起，對鋼管混凝土力學性能的研究越來越多[7-11]。目前對帶缺陷鋼管混凝土柱承載能力的研究中，對在缺陷隨機分布下的情況研究較少。葉勇[12]設置上、下貫通的均勻脫空缺陷，通過改變脫空率研究缺陷對軸壓承載能力的影響。張戎令等[13]設置的缺陷位置只考慮中心缺陷和邊側缺陷。劉開[14]在設置缺陷時，考慮了角部空洞、脫空、中央長方體、中央正方體和中央圓柱體等缺陷類型，并根據不同缺陷率設置不同的缺陷尺寸。門有冬[15]分別研究了孔洞缺陷、環形脫空缺陷和球冠形脫空缺陷對鋼管混凝土承載力的影響。李永進等[16]以脫空率和脫空類型為主要參數研究長期荷載對帶脫空缺陷混凝土受力性能的影響，其中脫空類型有通長均勻脫空缺陷和通長球冠形脫空缺陷。張傳欽等[17]以軸壓比、彎扭比為主要試驗參數，研究脫空缺陷對壓彎扭構件力學性能的影響，其設計的缺陷類型為球冠形缺陷，以脫空處核心混凝土邊緣到鋼管內壁的距離與構件截面外直徑的比值來定義缺陷率。廖飛宇等[18]設置環向脫空缺陷研究鋼管混凝土構件在壓彎扭復合受力作用下的滯回性能。

綜上所述，現階段對帶缺陷鋼管混凝土柱力學性能的研究中，模擬缺陷時人為干擾成分較多，忽略了缺陷實際存在的隨機性。本文基于ABAQUS/Python的二次開發，實現了不同缺陷大小與位置的隨機生成及結果自動提取；得到不同隨機缺陷類型對應的結構承載力，從而總結缺陷對結構承載力的影響規律。

1 建立有限元模型

1.1 材料本構關系選擇

本文所建模型中鋼材的本構模型選用理想型彈塑性模型，采用Von-Mises屈服準則，其應力-應變關系曲線如圖1所示[3]。核心混凝土本構模型采用混凝土損傷塑性模型，該模型可以很好地模擬混凝土構件的塑性與非線性特性，其假定材料的彈性行為是各向同性和線性的，而單軸拉伸和壓縮損傷塑性部分的力學行為由損傷塑性描述。

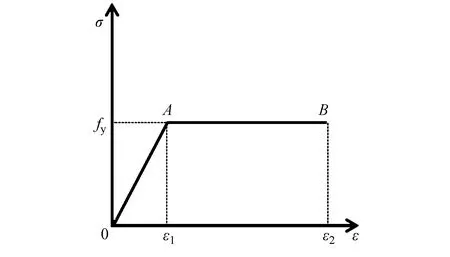
圖1 鋼管本構關系

設計模型的基本參數為：方鋼管邊長為400mm，壁厚6mm，長1.2m；上、下受力剛性板邊長為440mm，厚50mm。混凝土非缺陷集合單元和鋼管的主要計算參數為：混凝土密度2 600kg/m3，彈性模量3.7×104MPa，泊松比0.2；鋼管屈服強度330MPa，彈性模量2.1×105MPa，泊松比0.3。缺陷區域的單元假定為正常彈性模量的1/20，即為1.5×103MPa，端部受力剛性板的彈性模量取鋼材的100倍，不考慮其非線性。依據 GB 50010—2010《混凝土結構設計規范》中相關公式和參數及相關文獻計算核心混凝土塑性損傷模型參數，膨脹角為40°，偏心率為0.1，fb0/fc0為1.16，不變量應力比K為0.667，黏滯系數為0.000 5。依照模型尺寸確定混凝土各頂點處的坐標值：xbot=-197，xup= 197，ybot=-197，yup= 197，zbot= 0，zup= 1 200(見圖2)。

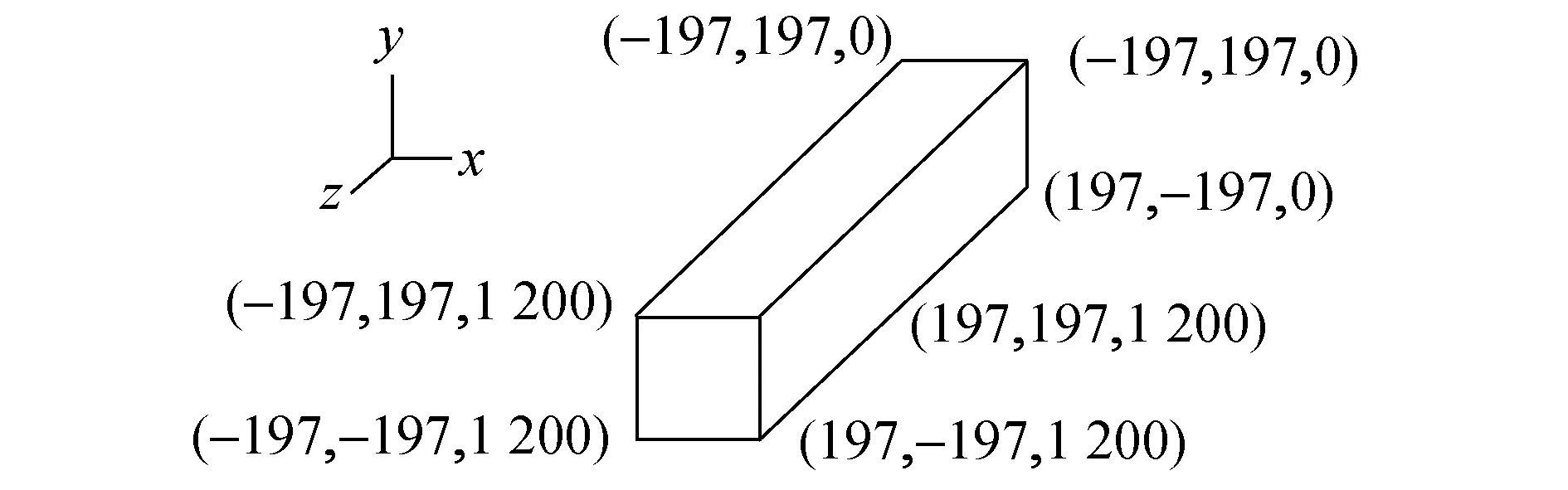
圖2 鋼管混凝土柱核心區混凝土模型

1.2 單元選取

鋼管的厚度尺寸相較于整體尺寸很小，其計算單元采用4節點減縮積分格式的殼單元來模擬，殼單元厚度方向采用9個積分點的Simpson積分方法，核心混凝土和兩端受力板采用8節點減縮積分格式的三維實體單元。

1.3 網格劃分

考慮到在分析接觸時，剛度更大的鋼管為主表面，核心混凝土為從屬表面，從屬表面的網格密度不能低于主表面[3]。為確定結果的網格穩定性，采用試算法確定網格密度，模型建立后，先采用較粗糙的網格進行模擬，然后不斷精細網格布置，直至最終確定，網格單元數-承載力曲線如圖3所示。

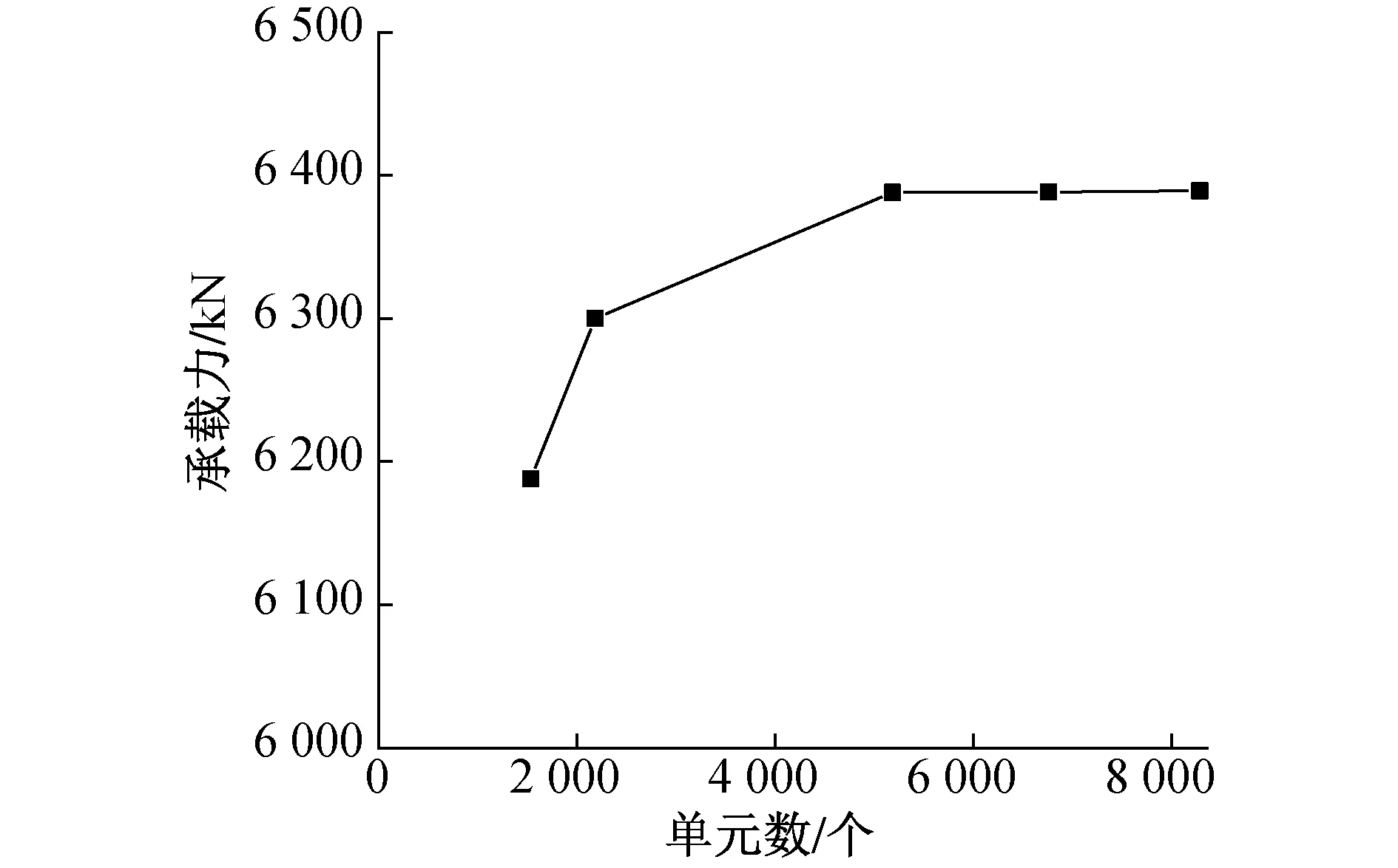
圖3 網格單元數-承載力曲線

1.4 界面接觸

鋼管混凝土模型的相互作用采用表面與表面接觸，定義接觸屬性時，法線方向的接觸采用“硬”接觸，切線方向摩擦公式定義為“罰”[19]，當達到極限臨界摩擦值時，界面間開始發生相對滑移，伴隨剪應力傳遞停止。

1.5 加載方式與邊界條件

在鋼管柱兩端設置大剛度受力板以提高計算的收斂性，設置其與鋼管混凝土為綁定連接。在下部受力板施加三向位移約束。加載方式為在上部剛性受力板上設置參考點，將參考點與上部鋼板耦合，對特征點進行位移加載。

2 隨機有限元二次開發

構建缺陷時，主要考慮缺陷的大小和位置，假定缺陷的形狀為球形，因此主要構件參數有球體半徑大小和圓心坐標。基于此，利用Python語言創建隨機缺陷的步驟如圖4所示。

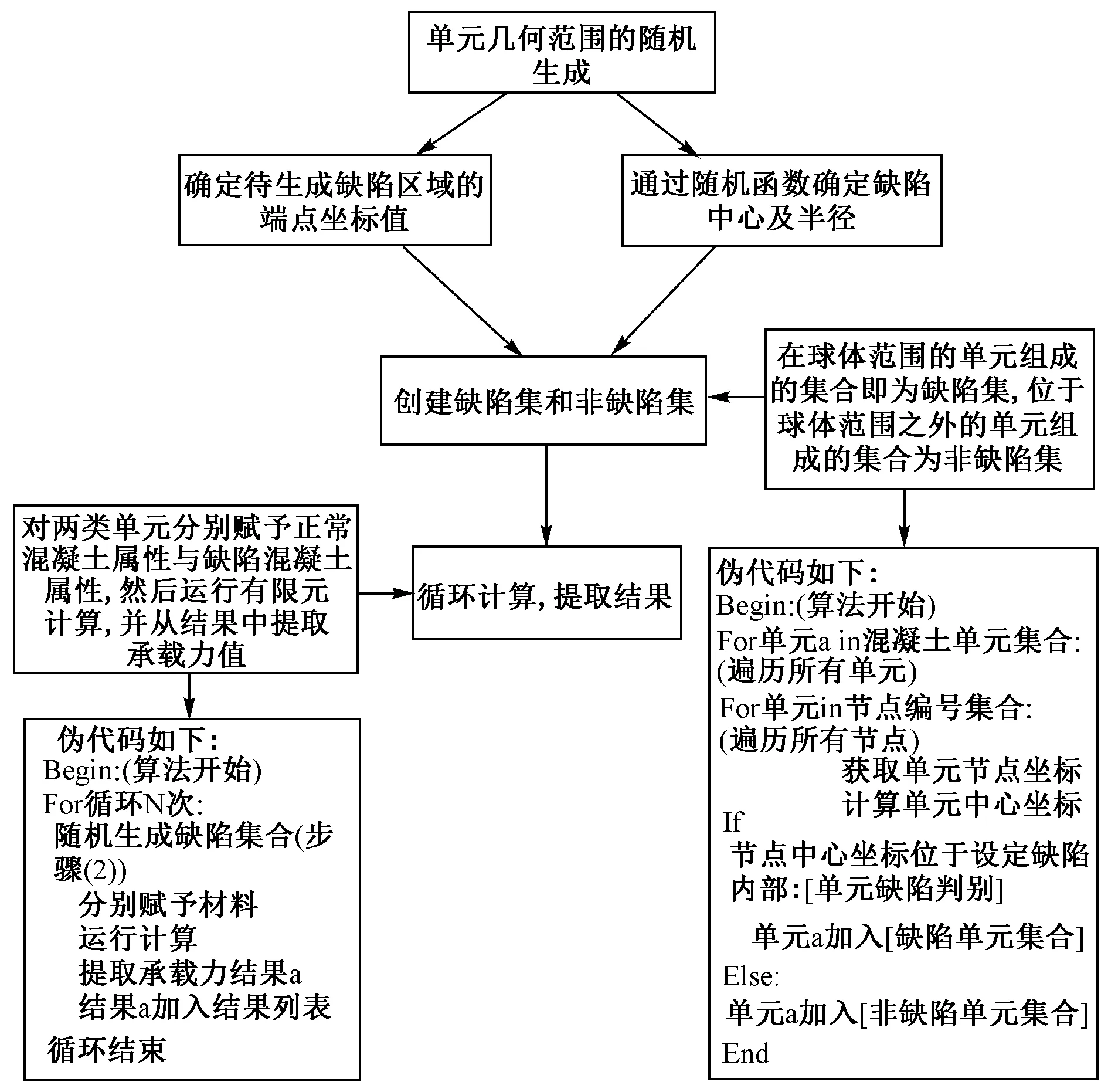
圖4 隨機缺陷生成流程

基于此開發鋼管混凝土有限元模型混凝土缺陷隨機生成軟件，操作界面及生成缺陷如圖5所示。在此操作界面上可選擇設置缺陷的形狀，模擬次數，缺陷模式，混凝土模型在三維空間中x，y，z方向的上、下限，生成隨機缺陷位置和形狀的模式與參數。設置完成后，點擊繪圖可在繪圖區生成隨機缺陷模型，點擊導出，可自動生成缺陷模型腳本文件。

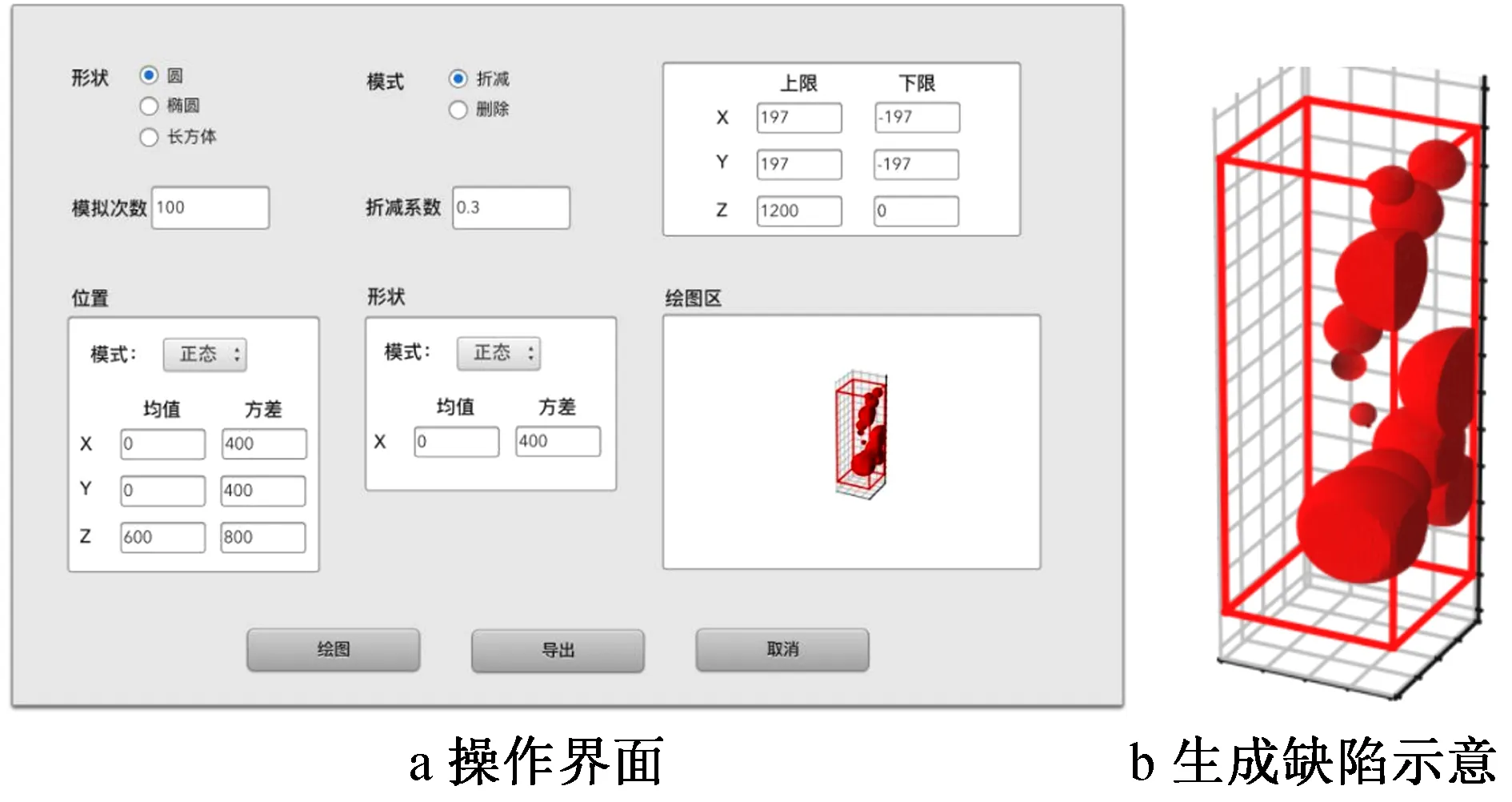
圖5 隨機缺陷生成軟件界面及生成缺陷

3 計算結果分析

3.1 承載力結果統計分析

在ABAQUS中建立好鋼管混凝土模型后，在缺陷生成軟件中確定好缺陷的設計參數，然后自動生成Python腳本，在ABAQUS中運行腳本，進行隨機有限元計算。鑒于最終計算得到的結果較多且篇幅有限，截取部分隨機缺陷數據如表1所示。

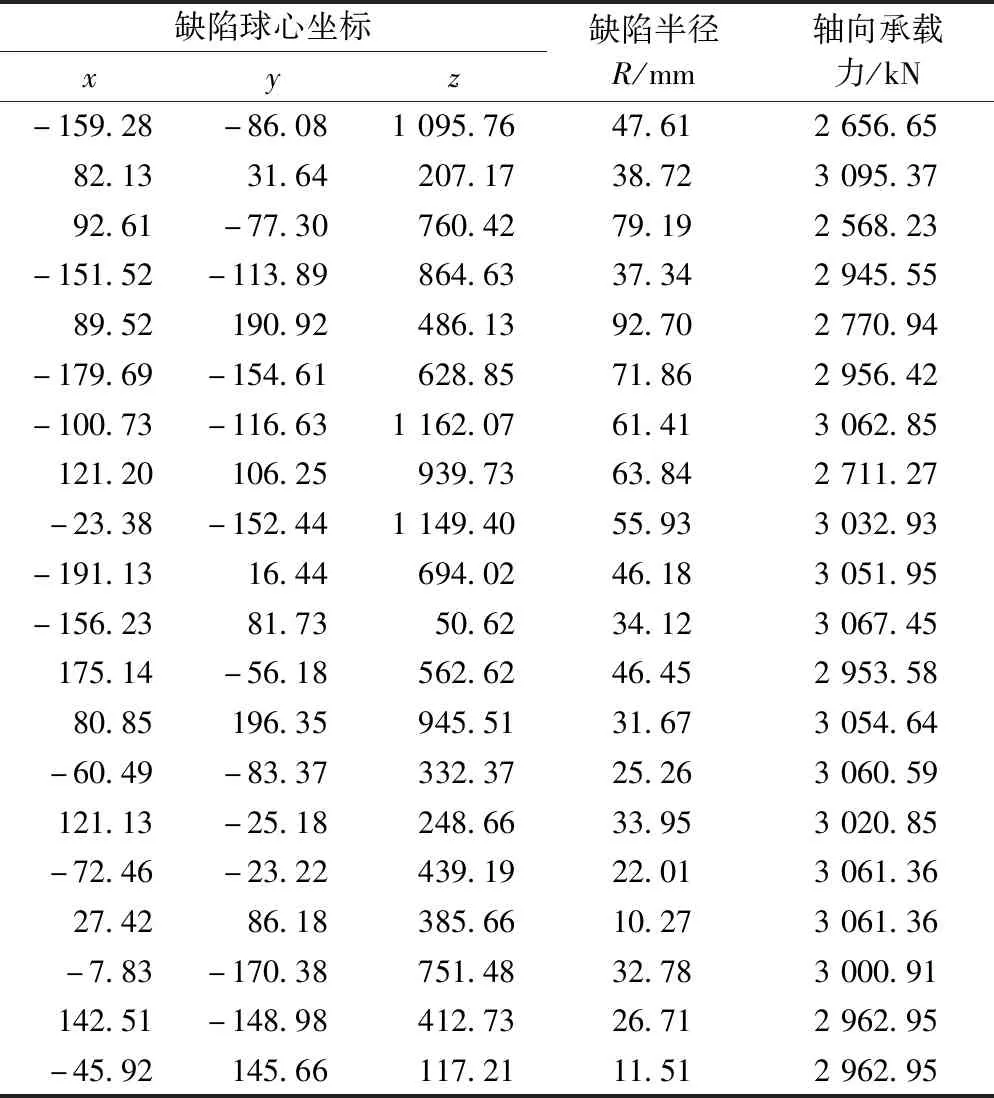
表1 部分隨機缺陷數據

計算共分2組，對應不同缺陷半徑的均值和方差，第1組均值為60，方差為40；第2組均值為30，方差為10。2組缺陷對應的鋼管混凝土有限元模型承載力頻率直方圖及得到擬合的曲線如圖6所示，承載力數值統計特征如表2所示。用K-S法對2組數據進行正態性檢驗，確定其分布是否滿足正態分布，顯著性水平為0.05，檢驗結果為：①第1組 均值為2 817.85kN，標準差為225.61，P=0.000 181(P表示數據的顯著性)；②第2組 均值為 3 008.15kN，標準差為66.04，P=0.000 002；兩組數據的顯著性均<0.05，不滿足正態分布。

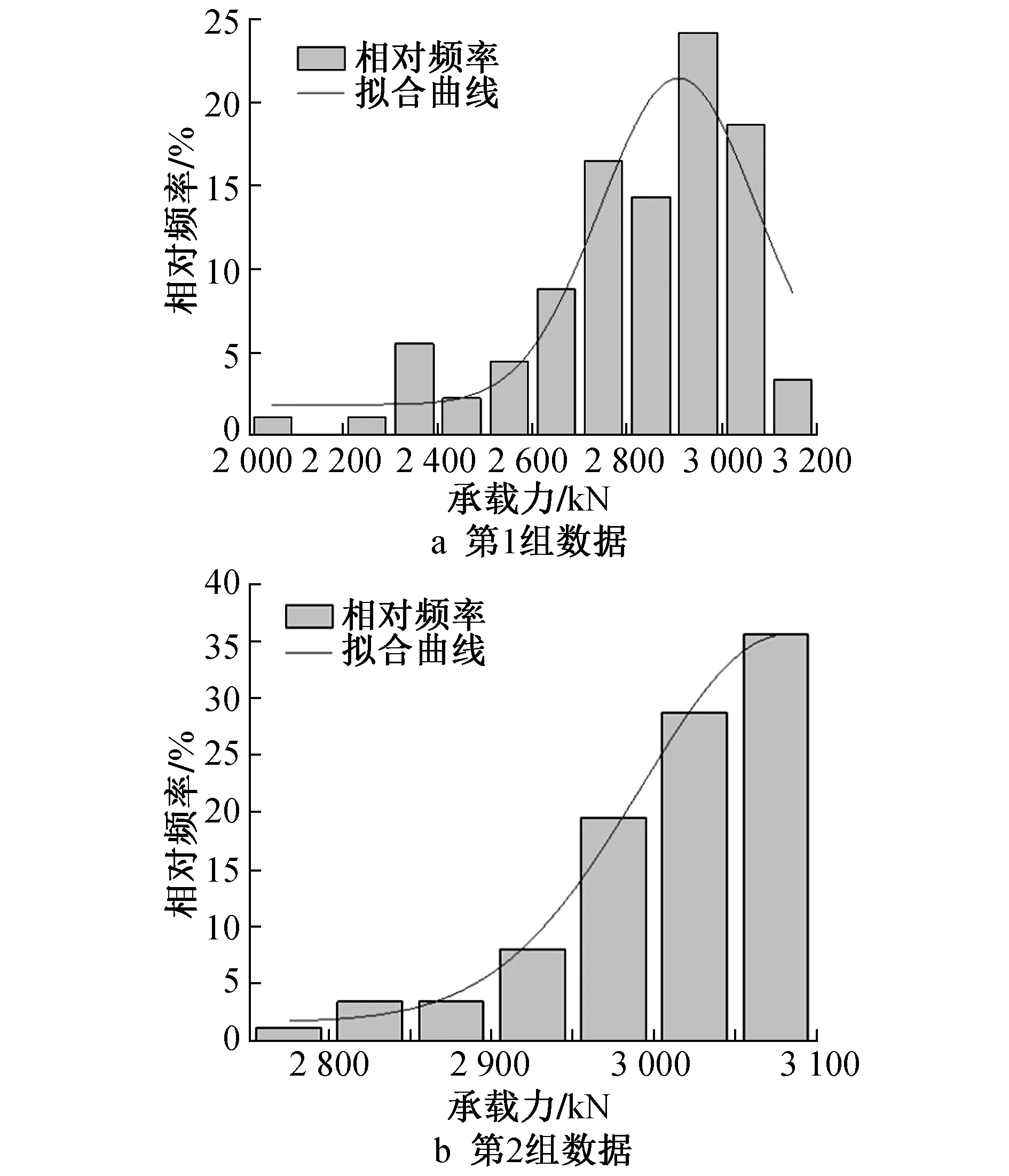
圖6 承載力頻率直方圖

表2 承載力統計特征

由圖6可知，曲線最高點均偏向于x軸右邊，位于右半部分曲線比正態分布曲線更陡，而左半部分曲線較平緩，其尾線比右半部分曲線更長，無限延伸到接近x軸；2組數據均滿足平均數<中位數<眾數的關系，考慮2組數據滿足偏態分布。計算得第1組數據的峰度為0.92，偏度為-1.07；第2組數據的峰度1.52，偏度為-1.33。對于呈現偏態分布的數據，可利用Box-Cox變化減弱其偏態狀況，更接近于正態分布[20]，用x表示原始數據，y表示變化后得到的數據，其計算公式如下：

(1)

分別對這2組數據進行Box-Cox變化，通過Minitab軟件先確定參數λ的估計值如圖7所示。由圖7可知，2組數據中λ的最優值均>5，最后得到2組數據的λ值分別為7.6，24。對變換后的數據通過SPSS分析軟件，利用K-S法進行正態性檢驗，得到P1=0.074>0.05，P2=0.052>0.05，說明2組變換后的數據均服從正態分布。

圖7 Box-Cox變換中的參數λ

3.2 缺陷率對軸壓承載力的影響

為研究缺陷率大小對結構承載力的影響，應先控制缺陷的分布范圍，本文主要通過缺陷的球心坐標來確定缺陷的位置分布。針對2組參數下隨機生成的球心坐標劃分的范圍為：x方向-98.5～98.5mm，y方向-98.5～98.5mm，z方向500～700mm；即選取的缺陷分布范圍大致位于核心混凝土中心區域，具體如表3所示。

表3 中心區域隨機缺陷

根據表3中計算出各類缺陷的缺陷率及對應結構的承載力折減系數，其中折減系數定義為帶缺陷結構軸向承載力與無缺陷結構軸向承載力的比值，經計算不帶缺陷鋼管混凝土模型的承載力為4 781.07kN，得到缺陷率-折減系數折線如圖8所示。

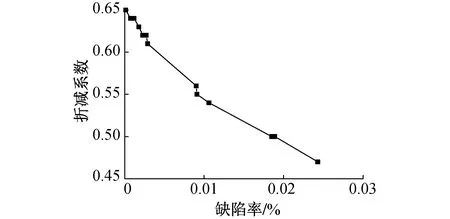
圖8 缺陷率-折減系數折線

由圖8可知，隨著缺陷率的增大，折減系數整體呈下降趨勢，即構件軸向承載力隨缺陷率的增大而減小。當缺陷率較小時，即在缺陷率≤0.005%的情況下，折線的斜率最大，平均斜率達到14.6，這表明在這一范圍內結構的軸向承載力下降最快；當缺陷率為0.005%～0.01%時，折線的平均斜率為8.2，當缺陷率>0.01%時，折線的平均斜率為5.1，這表明隨著缺陷率的增大，軸向承載力雖下降，但下降趨勢逐漸變緩。即使缺陷率很小的情況下，其軸向承載力也減小近40%，核心區混凝土內部缺陷的存在對結構承載力的影響很大，不容忽視。

3.3 缺陷位置對軸壓承載力的影響

為研究缺陷位置對結構軸壓承載力的影響，先將結構內核心混凝土劃分成不同區域，再選取1個缺陷率范圍，該范圍內的隨機缺陷在各區域內均有分布，每個隨機缺陷均對應有結構的軸向承載力，通過計算各區域軸向承載力的平均值并進行比較，從而找出缺陷位置對結構軸向承載力的影響。區域劃分以缺陷球心坐標為依據，共有以下幾部分：①區域ax方向-100～100mm，y方向-100～100mm，z方向300～900mm，即混凝土的中心區域；②區域b 相較于區域a，z軸數值不變，x，y軸坐標位于區域a對應位置以外，即混凝土中間部分靠近兩側的區域；③區域cx方向-100～100mm，y方向-100～100mm，z方向0～300mm，900～1 200mm，即混凝土兩端靠近中間的區域；④區域dz方向坐標與區域c一致，x，y方向坐標位于區域c對應位置以外，即混凝土兩端靠近兩側的位置。各區域對應部分具體信息如表4～7所示。缺陷不同區域的結構承載力直方圖如圖9所示。

由圖9可知，當缺陷位于c區域時，結構承載力普遍較大，其承載力>3 050kN的頻率可達40%；當缺陷位于區域a時，結構承載力主要集中在2 400～2 800kN，其頻率可達60%；當缺陷位于區域b時，結構承載力主要集中在2 900～2 950kN,其頻率為40%；當缺陷位于區域d時，結構承載力主要集中在2 700～2 900kN,其頻率為60%。通過計算，各區域對應軸向承載力的平均值如下：區域a為2 662.86kN，區域b為2 863.66kN，區域c為3 001.98kN，區域d為2 873.54kN，通過比較可得c>d>b>a。當缺陷位于結構兩端靠近中間部位時，缺陷對結構軸向承載力的影響最小；當缺陷位于結構兩端兩側位置和結構中間兩側位置時，即當缺陷位于邊部位置時，無論其在結構兩端還是結構中間位置，其對結構軸向承載力的影響基本相同；當缺陷位于結構的中心部位時，結構的軸向承載力平均值最低，對結構軸向承載力的影響最大。

表4 區域a隨機缺陷

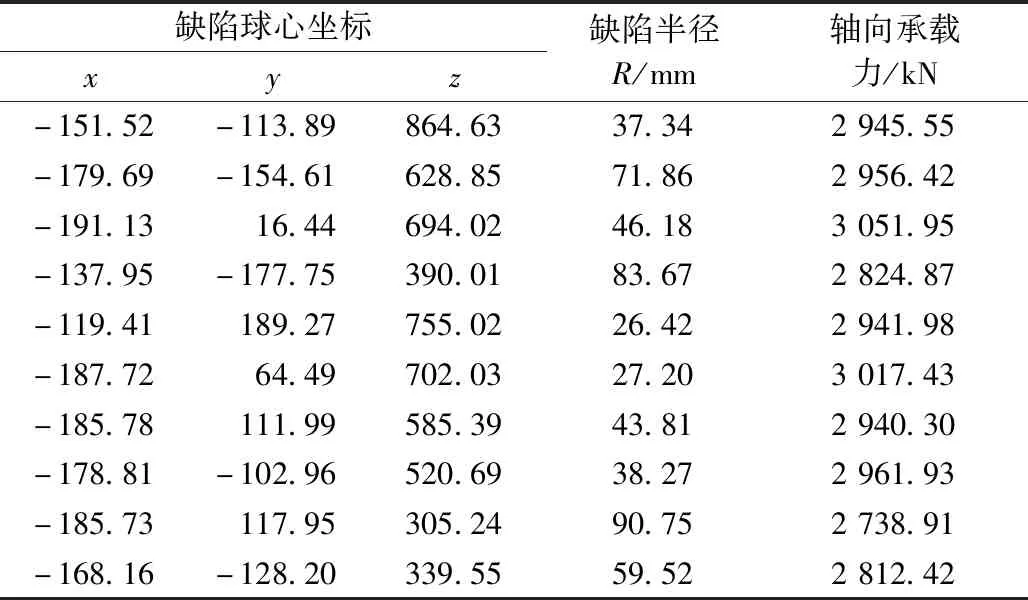
表5 區域b隨機缺陷

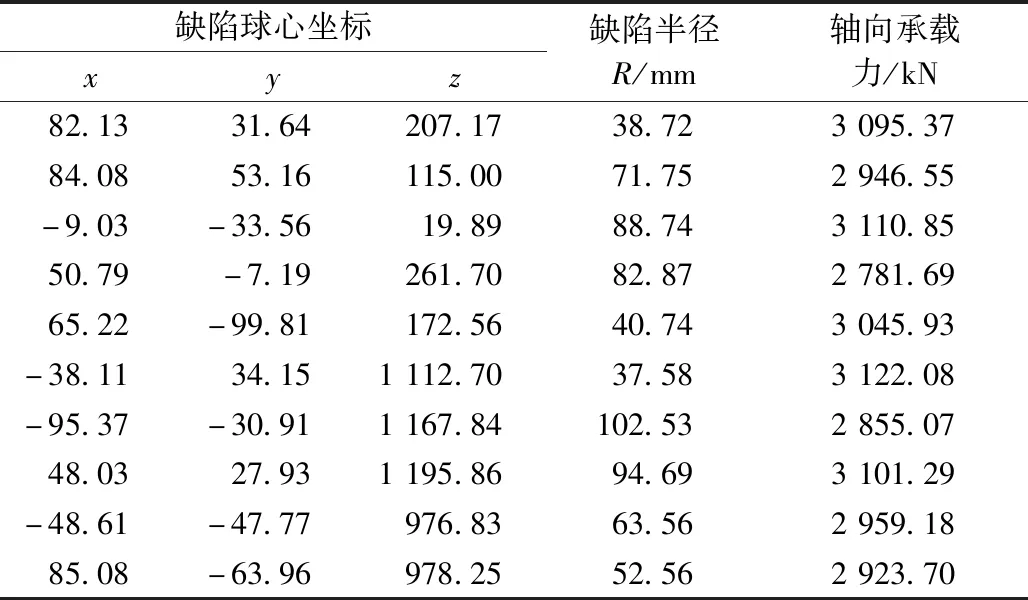
表6 區域c隨機缺陷

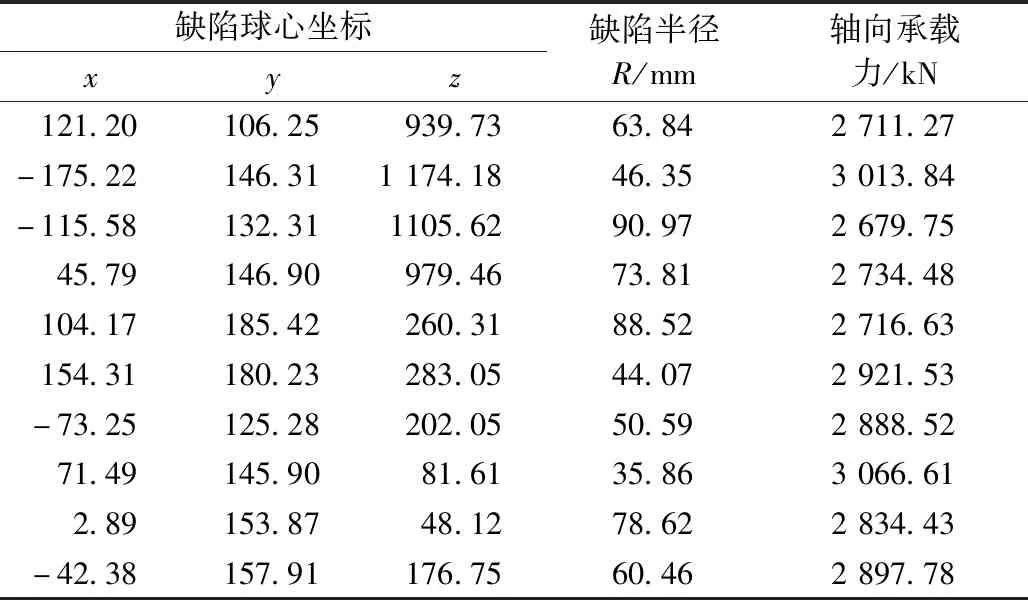
表7 區域d隨機缺陷

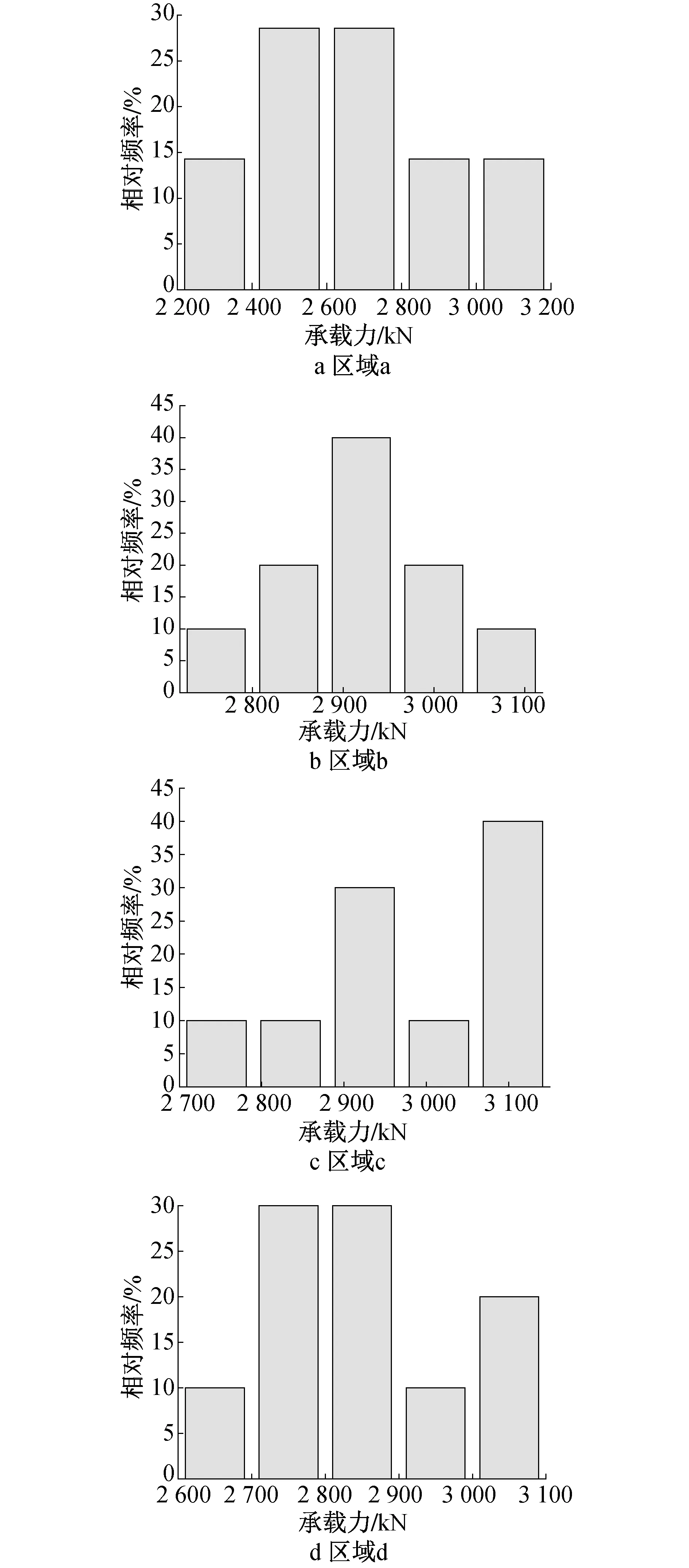
圖9 缺陷不同區域的結構承載力直方圖

4 結語

1)通過對大量承載力數值進行統計分析可發現，帶缺陷鋼管混凝土柱承載力數值維持在一定的范圍內，且服從偏態分布。

2)混凝土內部缺陷的存在對鋼管混凝土柱軸向承載力的影響很大，在缺陷率很小的情況下，軸向承載力的折減就能達到40%以上；結構承載力隨缺陷率的增大而降低，當缺陷率較小時，結構承載力下降很快，隨著缺陷率的增大，結構承載力下降開始變緩。

3)當缺陷位于核心混凝土中心部位時，對結構的承載力影響最大；位于核心混凝土兩端靠近中間位置的缺陷對結構承載力影響最小，當缺陷位于核心混凝土邊部位置時，對結構承載力的影響位于上述2種情況之間。