空氣阻尼網孔式彈性墊減振單元理論模型研究
和振興, 白彥博, 包能能, 贠劍峰, 石廣田
(蘭州交通大學 機電工程學院,蘭州 730070)
彈性墊層廣泛應用于建筑、兵工、軌道交通等領域的大型構筑物或裝備,降低地震或系統自身振動引起的不利影響。張玉良等[1]建立了橡膠墊支座雙向耦合彈塑性恢復力模型,并采用無條件穩定逐步積分方法,對建筑領域采用的橡膠墊隔震結構進行了優化;趙雷雷等[2]研究發現節流閥片開度是影響特種車輛減振器阻尼特性的關鍵數,并通過有限元仿真得到了其阻尼力隨閥片開度的變化規律;孫船斌等[3]研究了減震墊剛度、軸向尺寸等對導彈橫向振動特性的影響規律,為導彈水下發射系統的結構設計及優化提供了理論依據與研究手段;楊俊等[4]將Berg摩擦力單元與標準線性固體分數微分本構模型并聯,得到一種可以描述軌道交通車輛橡膠減振器黏彈性與彈塑性的非線性橡膠模型,較好地描述了橡膠墊動剛度和阻尼隨頻率、幅值變化的特征;孫亮明等[5]提出了一種應用于高架軌道橋梁的新型橡膠減振支座。通過增大橡膠塊傾角、橡膠層總厚度降低新型支座的壓縮剛度,進而提高其減振性能。韋凱等[6-7]以TPEE型彈性墊板為研究對象,建立車輛-軌道垂向耦合隨機振動分析模型,得到彈性墊板頻變、幅頻變剛度對輪軌耦合系統隨機振動的影響;崔旭浩等[8]建立了考慮道砟墊的高速鐵路有砟軌道離散元模型,研究發現鋪設道砟墊可以有效的降低道床剛度,增大有砟軌道彈性,從整體上降低有砟道床的振動水平。
上述減振墊、彈性支座等彈性層一般由橡膠、聚氨酯等彈性材料制成。提高阻尼對于彈性墊減振、隔震性能是有利的[9],但其阻尼主要由材料性質決定,制約了目前減振墊阻尼的提高。因此,對于阻尼要求更高的場合則采用造價更高的空氣彈簧或油壓彈簧。
彈性墊一般都采用橡膠等彈性材料制成,考慮到彈性材料的不可壓縮性,對于軌道列車走形基礎的彈性墊,一般制成溝槽型或棱臺型。和振興等[10-11]提出了一種帶高阻尼填充物的正六邊形網孔式彈性墊板,并對其結構進行了優化研究,但這種結構采用特殊的阻尼填充材料,彈性墊板加工成本較高。研究團隊提出了一種具有空氣阻尼的網孔式彈性墊板結構[12],為了研究其剛度和阻尼特性,本文建立了具有空氣阻尼的網孔式彈性墊層理論模型和有限元模型,研究了節流孔孔徑、氣室體積比對彈性墊剛度和阻尼特性的影響規律。
1 結構與模型
1.1 空氣阻尼網孔式彈性墊結構
本文研究的空氣阻尼網孔式彈性墊層至少由彈性差異較大的兩種材料制成,彈性墊的強變形層由彈性較大的材料制成,彈性墊的弱變形層由彈性較小的材料制成;利用網孔式結構的空腔在彈性墊層形成氣室,其中在強變形層中形成的氣室為主氣室,在弱變形層中形成的氣室為附氣室。兩種氣室之間用節流孔聯通[13]。
當彈性墊受到外部垂向載荷的作用時,強變形層首先產生較大的形變位移,弱變形層基本不產生垂向位移。主氣室內空氣受壓縮后經節流孔流入附氣室中,載荷卸去時,強變形層又恢復到初始位移量,附氣室內的壓縮空氣又經節流孔流入到主氣室。假設對彈性墊施加固定頻率的循環動載荷,上述過程將往循環進行,由于氣體在兩氣室之間往復流動,在通過節流孔時,會產生阻尼從而達到緩沖振動的目的。
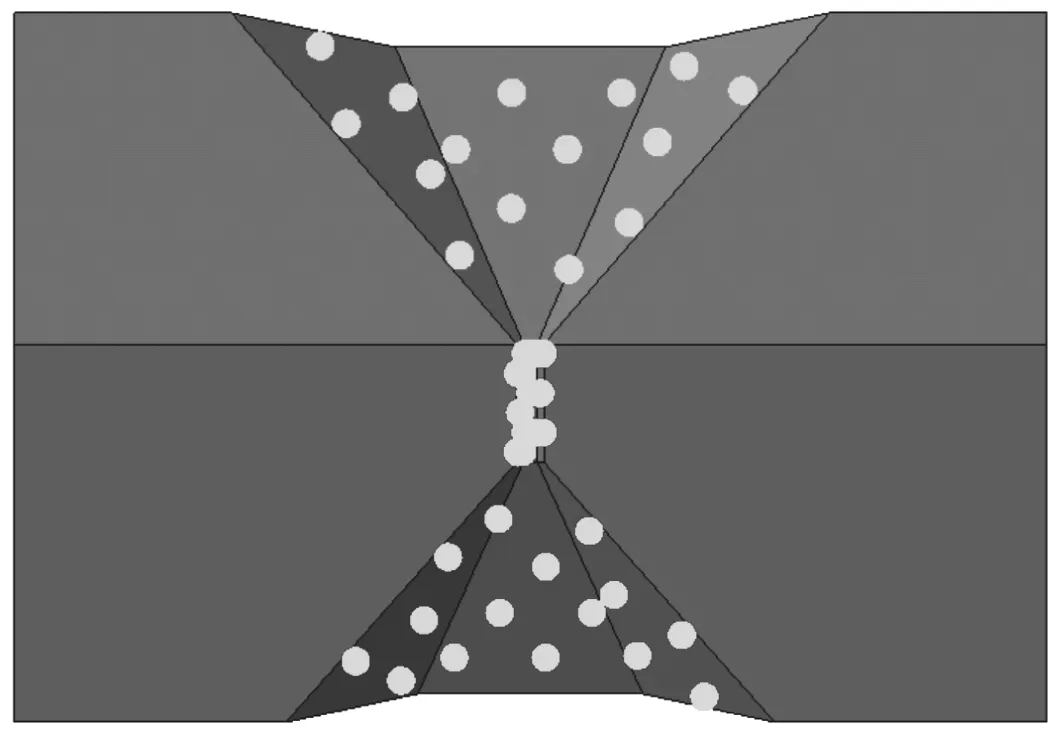
空氣阻尼網孔式彈性墊可以看成是由一個具有空氣阻尼的網孔式彈性墊減振單元在平面內通過陣列而成的。該彈性墊板整體尺寸為:300 mm×225 mm×30 mm,整板網孔數為:86個,其彈性墊整板結構如圖1所示。在彈性墊整板上表面網孔間中線處截取一單元,其結構如圖2所示。
1.2 動剛度和阻尼比
動剛度和阻尼比是彈性墊層的關鍵動力學參數,空氣阻尼網孔式彈性墊減振單元的動剛度取決于其載荷和位移,空氣阻尼網孔式彈性墊減振單元的動剛度Kd為[14-15]
(1)
式中:xm為最大荷載對應垂向位移與最小荷載對應垂向位移之間的差值;Fm為最大荷載與最小荷載之間的差值。
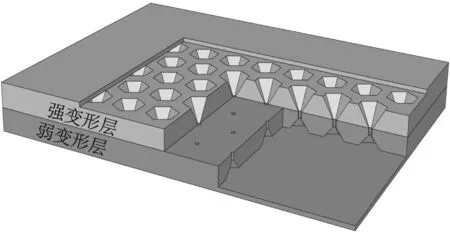
圖1 空氣阻尼網孔式彈性墊
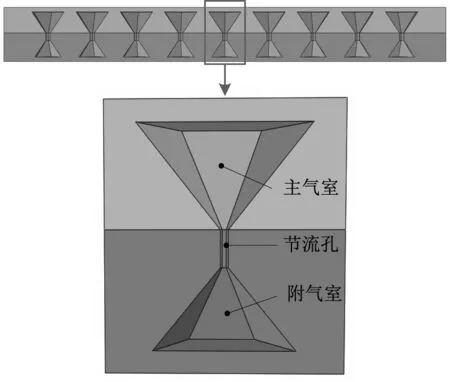
圖2 彈性墊減振單元結構
根據網孔型彈性墊層的結構特點可知:空氣阻尼網孔式彈性墊上網孔間中線處的垂向面為受力對稱面。受力對稱面在加載垂向荷載時只有垂向形變量,故沿著受力對稱面切割的單網孔模型的力學性能可等效于彈性墊板整板。根據既有研究可得[16]:空氣阻尼網孔式彈性墊減振單元結構的阻尼比與彈性墊整板的阻尼比計算結果基本相等,彈性墊層整板阻尼比ζz為
ζz≈ζd
(2)
(3)
(4)
式中:ζd為空氣阻尼網孔式彈性墊減振單元的阻尼比;δ為對數衰減率;An和An+k分別為空氣阻尼網孔式彈性墊減振單元自由振動衰減波形圖中第n個和第n+k個波峰值;k為波峰間隔周期數。
2 空氣阻尼網孔式彈性墊減振單元的數學建模
本文以空氣阻尼網孔式彈性墊的一個彈性減振單元結構為研究對象,其上部為容積較大的主氣室;中部為具有一定孔徑和長度的節流孔;下部為容積較小的附氣室。其主要用于承受垂向載荷,根據牛頓第三定律可知:該結構工作時承受的垂向載荷F等于橡膠結構產生的作用力F1和氣室內壓縮空氣產生的作用力F2,可表示為
F=F1+F2
(5)
F2=(Pa-Patm)Aa
(6)
Aa=A0+αΔz
(7)
式中:Pa為主氣室內氣體絕對壓力;Patm為標準大氣壓;Aa為空氣阻尼網孔式彈性墊減振單元的有效工作面積,A0為彈性墊減振單元在工作平衡點處的有效工作面積;α為有效工作面積變化率;Δz為彈性墊減振單元工作時的相對位移。
2.1 主氣室數學模型
假設主氣室內氣體為理想氣體,則滿足理想氣體狀態方程
PaV1=m1RT1
(8)
式中:V1為主氣室內氣體體積;m1為主氣室內氣體質量;R為氣體常數;T1為主氣室內氣體溫度。
考慮到彈性墊在工作過程中近乎為絕熱過程,所以主氣室內氣體變化遵循以下方程
(9)
式中:ρ1為主氣室內氣體密度;P1為主氣室內氣體壓強;下標為“10”表示主氣室內某參數的初始狀態量;上標為“′”表示工作在某一時刻某參數的狀態量;ε為氣體絕熱指數,取1.4;k為常數。
由于在彈性墊減振單元工作狀態下,主氣室內氣體質量變化滿足質量流量的連續性,所以主氣室內氣體質量流量方程為[17]
(10)
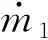
根據式(8)、(9)、(10)可求得主氣室內氣體質量流量為
(11)
由式(11)可知主氣室氣體壓強變化率為
(12)
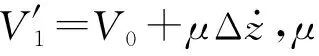
(13)
由式(13)可知:在彈性墊減振單元處于平衡點處時,氣體壓強變化率與主氣室內氣體質量流量和氣體體積變化有關。
2.2 附氣室數學模型
對于空氣阻尼網孔式彈性墊減振單元的附氣室,其內部氣體質量變化同樣滿足質量流量的連續性。同時,假設彈性墊的下半部分是不可壓縮的,即附氣室內的體積在彈性墊減振單元工作過程中是不變的。故有
(14)
根據式(11)、(14)可求得附氣室內氣體質量流量為
(15)
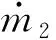
由式(15)可知,附氣室內氣體壓強變化率為
(16)
故在彈性墊減振單元工作平衡點處,即P20=P2,T20=T2時,有
(17)
由式(17)可知,附氣室內氣體壓強變化率與氣體質量流量有關。
2.3 節流孔數學模型
根據能量守恒定律和氣體質量流量連續性方程可得節流孔處氣體質量流量方程為
(18)
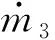
故在彈性墊減振單元工作平衡點處,即P1=P2時,有
(19)
由式(19)可知,節流孔處氣體質量流量與節流孔孔徑有關。
2.4 橡膠結構模型
由于空氣阻尼網孔式彈性墊減振單元的結構為上軟下硬,因此可以將此結構近似的等效為一個橡膠氣囊結構,橡膠氣囊結構模型包括:庫侖摩擦模型和分數開爾文-沃格特模型。
(1) 庫侖摩擦模型
對于橡膠彈性墊減振單元的庫倫摩擦模型,如圖3所示,其摩擦力與位移的關系如下[18]
當x=x0時,
Ff=Ff 0
(20)
當x>x0時,
(21)
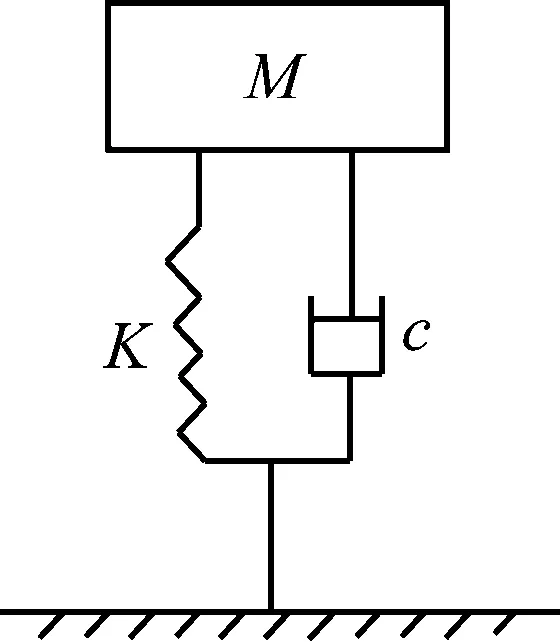
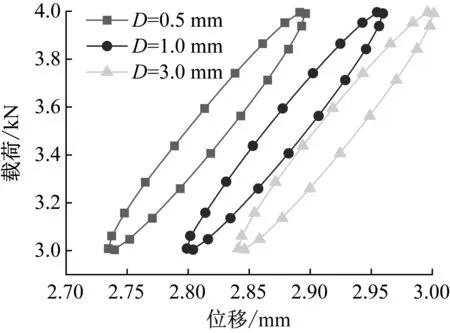
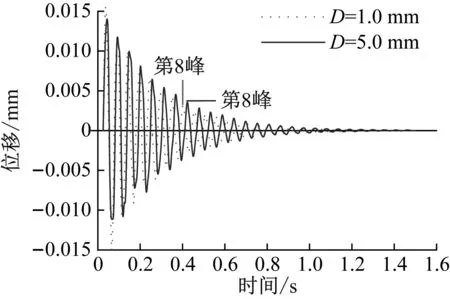
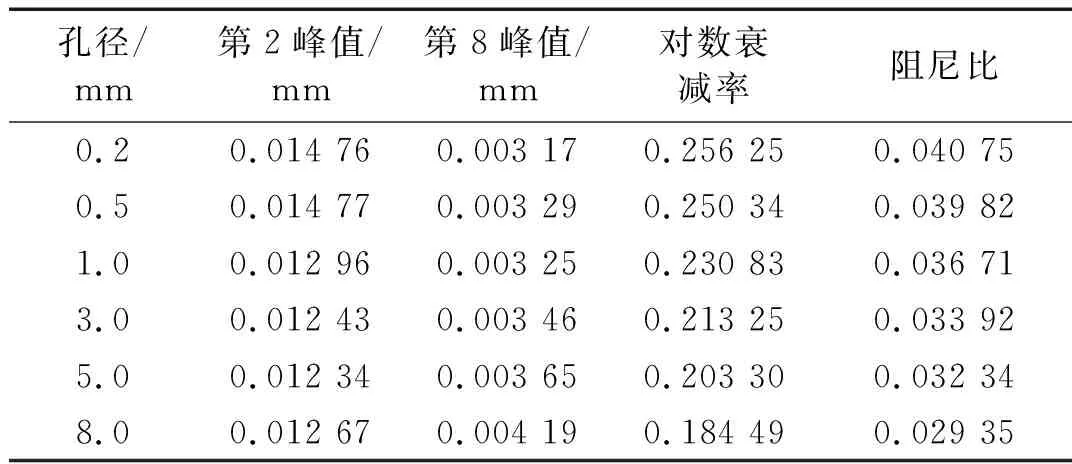
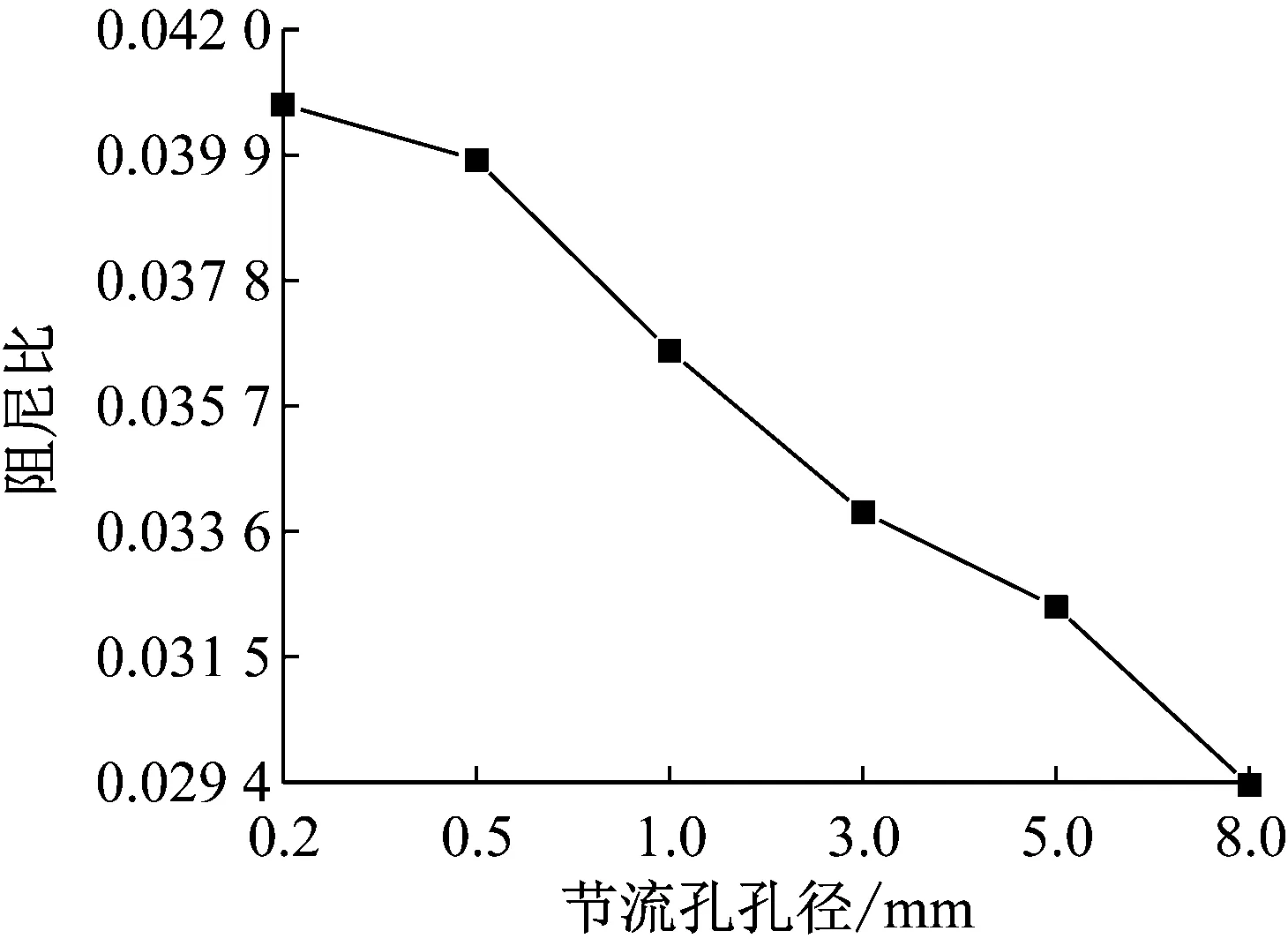
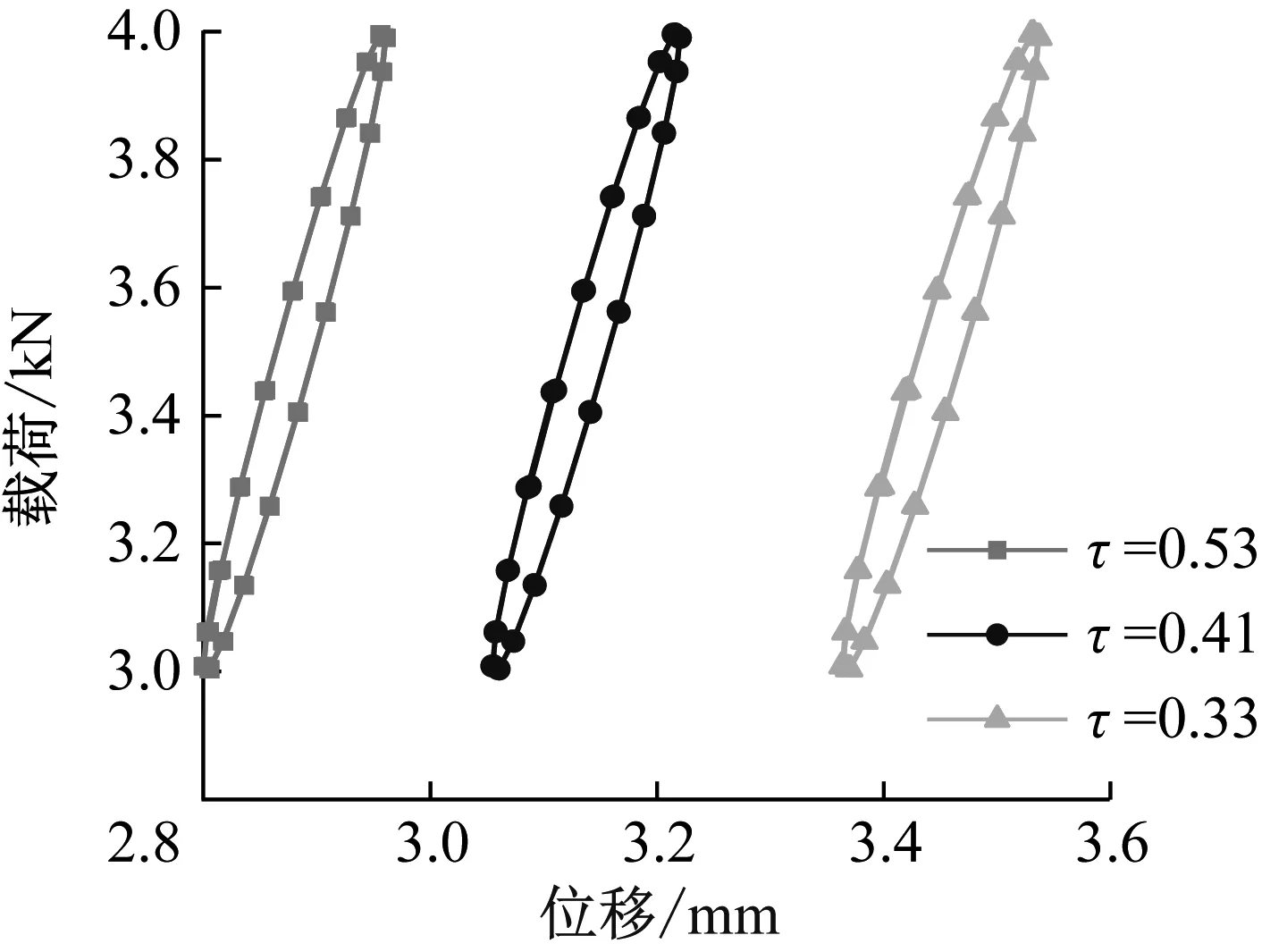
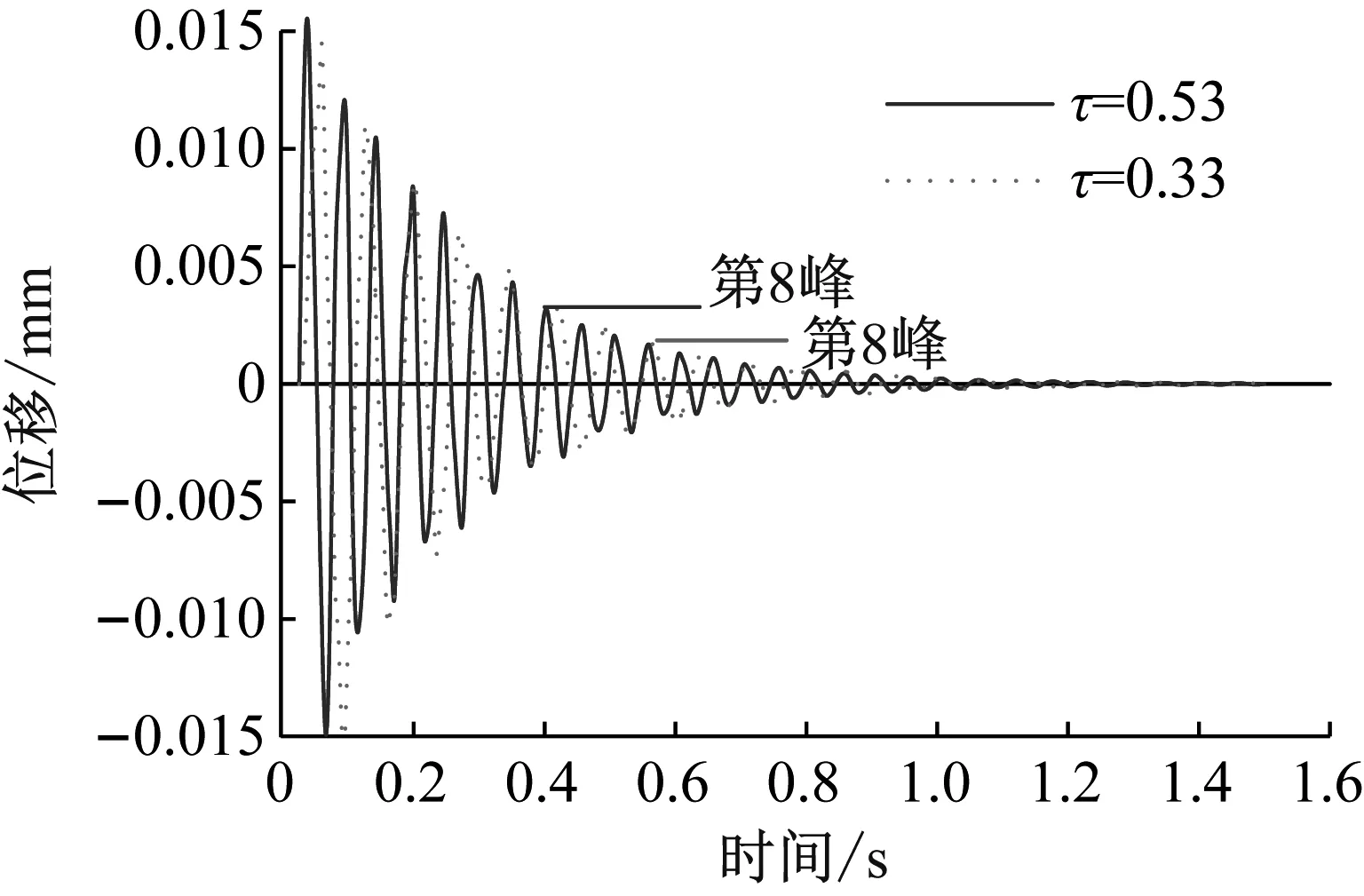
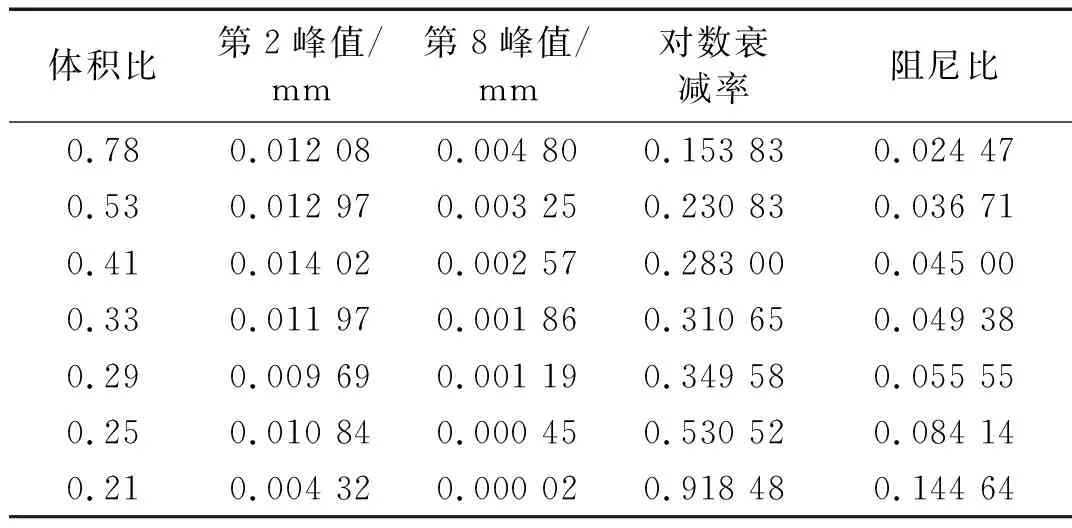
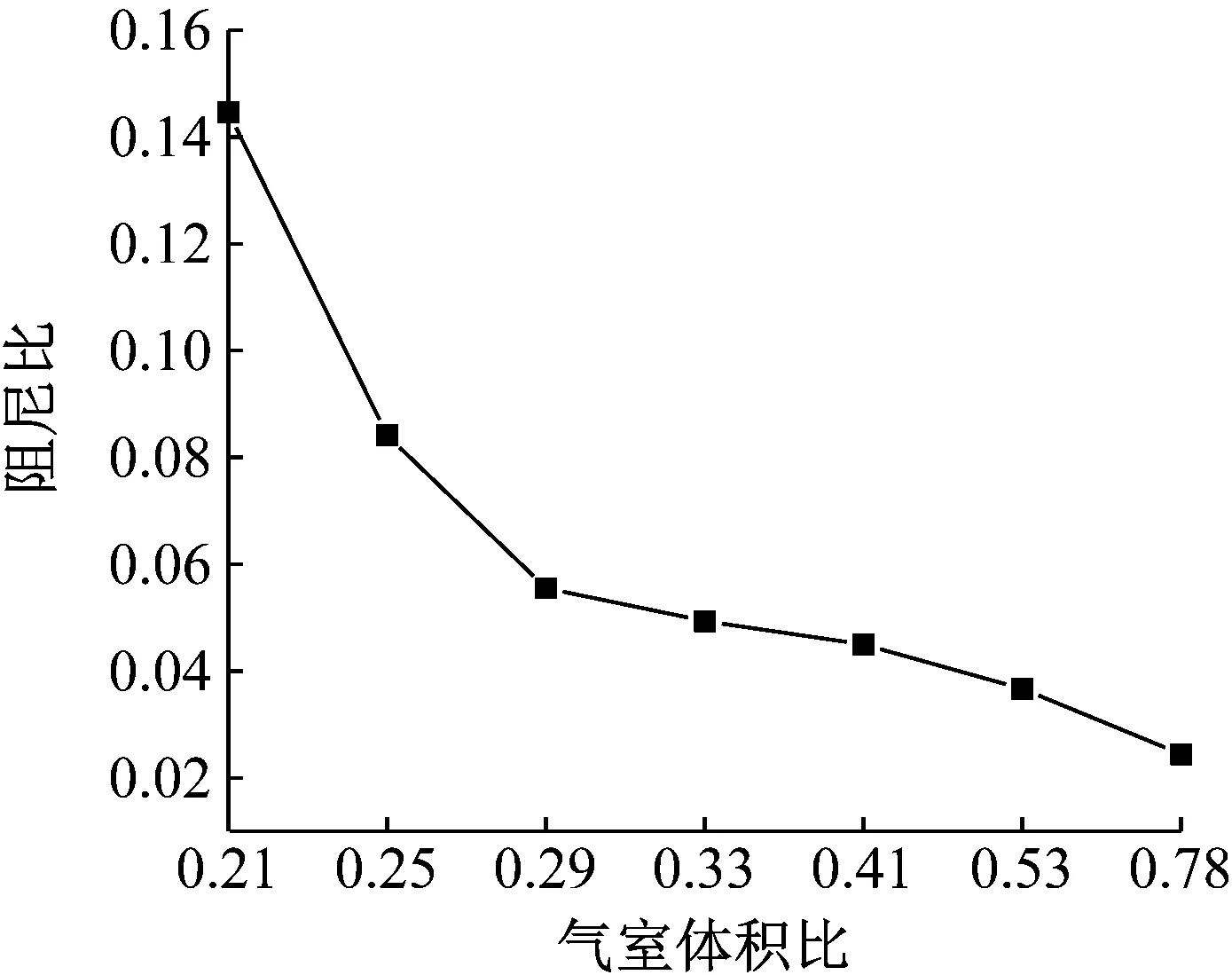
當x (22) 式中:Ff 0為初始摩擦力;x0為初始位移;Ff max為最大摩擦力;x1為最大摩擦力一半時對應的位移大小;θ=Ff 0/Ff max。 圖3 庫倫摩擦模型 根據模型穩態時的力幅值和每個周期的能量損失可得該模型的剛度Kf和阻尼Df為 (23) (24) 式中:Ff1為穩態時的力幅值;x2為輸入激勵的振幅;η=Ff1/Ff max。 由式(24)可知摩擦模型的滯后角為 (25) (2) 分數開爾文-沃格特模型 對于分數開爾文-沃格特模型,如圖4所示,其力和位移的關系為[19] F(t)=KLx(t)+aDbx(t) (26) 式中:KL為模型線剛度;a為分數阻尼系數;Dbx(t)為位移x的b階導數。 圖4 分數開爾文-沃格特模型 由式(26)可知分數開爾文-沃格特模型的動剛度和滯后角為 (27) (28) 為了方便計算,可將空氣阻尼網孔式彈性墊減振單元系統等效為單自由度的彈簧阻尼系統,如圖5所示。 圖5 單自由度質量彈簧阻尼系統 圖5中該系統的等效復剛度為 KX=K+jωc (29) 式中:KX為系統的等效復剛度;K為彈簧的線剛度;c為系統的阻尼系數;ω為系統的固有頻率;j為虛數單位。 根據式(5)、(13)、(17)、(19)、(23)、(25)、(27)、(29)可以得到該系統的復剛度為 (30) 其中: (31) (32) (33) (34) (35) Ks=-(P0-Patm)α (36) (37) (38) 式中:Rf為節流孔阻力系數;K1v為有效工作氣體體積僅為彈性墊減振單元主氣室內氣體的體積剛度;K12v為有效工作氣體為彈性墊減振單元主氣室和附氣室體積之和時的體積剛度;Ks為表面積剛度;C2為彈性墊減振單元附氣室氣容大小;τ為附氣室與主氣室體積之比,本文簡稱為氣室體積比。 由式(29)和(30)可知空氣阻尼網孔式彈性墊減振單元的等效剛度和等效阻尼系數為 (39) (40) 由式(39)和(40)可見,空氣阻尼網孔式彈性墊減振單元的等效剛度和等效阻尼系數主要取決于Rf和τ,由式(33)和(38)可知,Rf主要與節流孔截面積有關,τ為附氣室與主氣室體積之比。故空氣阻尼網孔式彈性墊減振單元的等效剛度和等效阻尼系數主要與節流孔的孔徑、氣室體積比設計參數有關。 為了進一步研究節流孔孔徑、氣室體積比對彈性墊剛度和阻尼系數的影響。以軌道交通道床類減振軌道板下彈性墊為例,選取一個結構單元建立有限元模型,通過模擬循環力荷載和落錘沖擊實驗,驗證節流孔孔徑和氣室體積比對彈性墊剛度和阻尼系數的影響規律。由于阻尼比ζ阻尼系數c呈正比關系[20],為了方便計算,可直接將阻尼系數等效為阻尼比進行分析驗證。由于空氣阻尼網孔式彈性墊減振單元結構的阻尼比與彈性墊整板的阻尼比計算結果基本相等,故本文選擇空氣阻尼網孔式彈性墊減振單元為研究對象。 在有限元仿真計算過程中,賦予該結構單元不同硬度的材料屬性,彈性較大的材料形成強變形層,彈性較小的材料則為弱變形層,在對空氣阻尼網孔式彈性墊減振單元進行動剛度特性研究時,要將彈性墊減振單元的垂向位移量控制在其總高度的10%左右,故對于30 mm的道床類減振軌道板下彈性墊,要將其垂向位移控制在3 mm左右。根據對有限元模型材料參數的調試,選擇空氣阻尼網孔式彈性墊減振單元強變形層的楊氏模量和泊松比分別取0.15 MPa和0.050,弱變形層的分別取0.21 MPa和0.499。填充于空氣阻尼網孔式彈性墊減振單元氣室中的空氣按24 ℃考慮,密度為1.29 kg/m3,黏度為1.82×10-5Pas。同時,在空氣阻尼網孔式彈性墊減振單元的上、下表面各添加一個剛體性蓋板,以便于載荷可以均勻的傳遞給下部結構,上、下蓋板與空氣阻尼網孔式彈性墊減振單元采用綁定約束。最后,建立流固耦合有限元模型實現兩者的仿真計算。其中,空氣阻尼網孔式彈性墊減振單元有限元網格如圖6所示。空氣單元有限元網格如圖7所示。兩者均劃分六面體網格,網格類型為:C3D8R。 圖6 空氣阻尼網孔式彈性墊減振單元有限元網格 圖7 空氣單元有限元網格 由于空氣阻尼網孔式彈性墊減振單元與空氣單元的耦合作用僅發生在兩者的相交界面上,故在兩者的外接面分別定義流固耦合界面,如圖8所示,通過聯合仿真可以實現兩者的協同響應,該耦合界面可以模擬空氣阻尼網孔式彈性墊減振單元在考慮內部空氣作用下產生變形。 圖8 有限元模型耦合界面的定義 保持空氣阻尼網孔式彈性墊減振單元結構和材料參數不變,對空氣阻尼網孔式彈性墊減振單元施加3~4 kN均勻分布的周期性正弦荷載,加載荷載的頻率為5 Hz。加載時間為10 s。由于空氣阻尼網孔式彈性墊減振單元在受到均布載荷時變形均勻,故在上蓋板中點處提取位移、載荷曲線。圖9是節流孔孔徑分別為D=0.5 mm、1.0 mm、3.0 mm時的動剛度對比圖。 圖9 不同孔徑條件下動剛度曲線 由圖9可見,隨著節流孔孔徑的增大,空氣阻尼網孔式彈性墊減振單元的動剛度曲線整體向右偏移,這是由于節流孔孔徑的改變,對彈性墊減振單元的結構有一定的影響,在相同荷載作用下,其初始位移將隨著節流孔孔徑的增大而增大。因此,空氣阻尼網孔式彈性墊減振單元的動剛度曲線因節流孔孔徑的變化而產生整體偏移。 由圖9可知,三種不同節流孔孔徑對應空氣阻尼網孔式彈性墊減振單元的垂向位移為:0.161 5 mm、0.160 6 mm、0.160 0 mm,由式(1)可得其動剛度值依次為:6.192 kN/mm、6.228 kN/mm、6.250 kN/mm。所以,空氣阻尼網孔式彈性墊的動剛度隨著節流孔孔徑的增大而增大。 采用上述有限元模型模擬沖擊荷載為1 kN的落錘沖擊實驗,得到不同節流孔孔徑下空氣阻尼網孔式彈性墊減振單元的自由振動衰減響應。圖10是節流孔孔徑分別為1.0 mm和5.0 mm時振動衰減的對比圖。圖10表明,由于阻尼的作用,空氣阻尼網孔式彈性墊減振單元的振動響應幅值隨時間的增大而衰減,其中節流孔孔徑為1.0 mm工況對應響應的初始幅值較大,但其衰減速度更快,說明其阻尼吸能效果更好。 圖10 不同孔徑條件下自由振動衰減曲線 選擇波峰趨于穩定的第2個和第8個峰值進行阻尼比的計算。波峰間隔周期數k=6,由式(3)、(4)可得不同節流孔孔徑條件下空氣阻尼網孔式彈性墊減振單元的阻尼比,結果如表1所示。其阻尼比隨節流孔孔徑的變化規律如圖11所示。 表1 不同節流孔孔徑條件下空氣阻尼網孔式彈性墊單元阻尼參數對比 圖11 阻尼比隨節流孔孔徑的變化規律 由表1和圖11可知,隨著節流孔孔徑的增大,空氣阻尼網孔式彈性墊減振單元的阻尼比隨之減小,通過對比計算可知,D=0.2 mm時的阻尼比相比于D=5.0 mm時提高了38.84%。而節流孔孔徑在小于0.5 mm后其阻尼比增長趨勢逐漸減緩,節流孔孔徑過小也不易生產加工,故可將空氣阻尼網孔式彈性墊減振單元的節流孔孔徑控制在0.5 mm左右。根據阻尼比等效原理可知,節流孔孔徑對彈性墊整板的阻尼比也具有同樣的影響規律。 為了研究氣室體積比對空氣阻尼網孔式彈性墊剛度和阻尼比的影響時,保持材料參數不變,改變附氣室與主氣室的體積比,加載方式與4.1節相同。圖12是體積比分別為0.33、0.41、0.53時,空氣阻尼網孔式彈性墊減振單元的位移-荷載曲線。 圖12 不同氣室體積比條件下的位移-載荷曲線 從圖12可見,改變氣室體積比,引起位移-載荷曲線的偏移,這主要是由于體積比變化對應結構參數變化導致彈性墊減振單元的靜剛度變化引起的。對比圖9和圖12可見,氣室體積比對墊板靜剛度的影響比節流孔孔徑顯著。 由圖12得出當彈性墊減振單元的體積比分別為0.53、0.41、0.33時,三種不同體積比對應空氣阻尼網孔式彈性墊減振單元的垂向位移為:0.160 6 mm、0.165 1 mm、0.172 7 mm,由式(1)可得其動剛度值依次為:6.228 kN/mm、6.058 kN/mm、5.789 kN/mm。所以,空氣阻尼網孔式彈性墊減振單元的動剛度隨著氣室體積比的減小而減小。 用有限元模型模擬落錘實驗,得到不同氣室體積比條件下空氣阻尼網孔式彈性墊減振單元的自由振動衰減波形如圖13所示。對比圖13中第2個和8個波峰的幅值可以看出,氣室體積比越小,振動的衰減速度越快。 圖13 不同氣室體積比條件下自由振動衰減曲線 選擇振動衰減曲線波峰趨于穩定的第2個波峰和第8個波峰峰值進行阻尼比的計算,波峰間隔周期數k=6,由式(3)、(4)可得不同體積比條件下空氣阻尼網孔式彈性墊減振單元的阻尼比,結果如表2所示。其阻尼比隨氣室體積比的變化規律如圖14所示。 由表2和圖14可見,隨著氣室體積比的減小,空氣阻尼網孔式彈性墊減振單元的阻尼比隨之增大。當氣室體積比小于0.29時,氣室體積比對阻尼比的影響顯著;當氣室體積比大于0.29以后,氣室體積比對阻尼比的影響趨緩。但氣室體積比過小會使空氣阻尼網孔式彈性墊減振單元的垂向位移量過大,造成主氣室變形嚴重,空氣阻尼網孔式彈性墊減振單元的動剛度過大。故彈性墊的氣室體積比要根據其應用場合的剛度要求而選擇較小的。 表2 不同體積比條件下空氣阻尼網孔式彈性墊減振單元阻尼參數對比 圖14 阻尼比隨氣室體積比的變化規律 (1) 通過對具有空氣阻尼的網孔式彈性墊減振單元的理論建模,并基于復剛度理論得出節流孔孔徑、氣室的體積比是影響彈性墊剛度和阻尼的關鍵參數。 (2) 對于空氣阻尼網孔式彈性墊,節流孔孔徑的變化對其動剛度和阻尼比都有一定的影響。隨著節流孔孔徑的增大,彈性墊的動剛度隨之增大,而阻尼的變化趨勢與剛度相反,當D=0.2 mm時的阻尼比相比于D=5.0 mm時提高了38.84%。 (3) 空氣阻尼網孔式彈性墊的氣室體積比變化對其動剛度和阻尼比有顯著的影響。減小氣室體積比,彈性墊的動剛度隨之減小;而阻尼比隨之增大,當氣室體積比小于0.29時,氣室體積比對阻尼比的影響顯著。 (4) 對比節流孔孔徑、氣室體積比對彈性墊剛度和阻尼的影響可知,節流孔孔徑和氣室體積比的大小對結構阻尼的影響比剛度更明顯。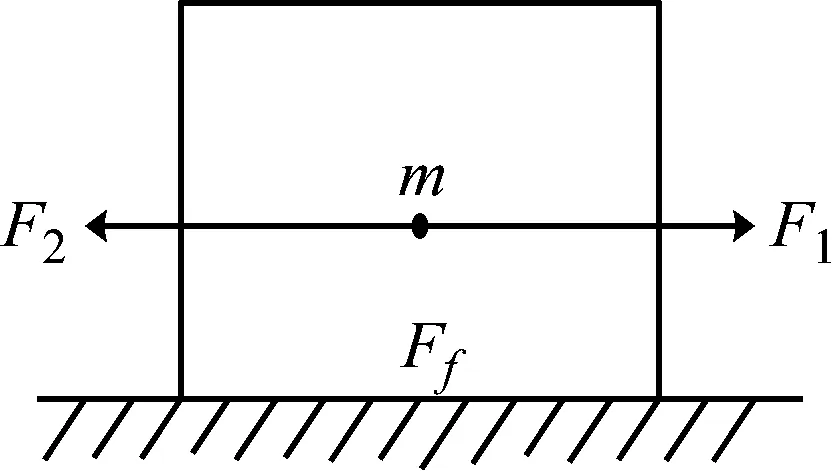

3 空氣阻尼網孔式彈性墊減振單元等效剛度和等效阻尼的計算
4 參數影響分析


4.1 節流孔孔徑的影響
4.2 氣室體積比的影響
5 結 論

